在轨高效目标检测加速技术

呼延烺，李 映，蒋冬梅，张艳宁，周 诠，魏佳圆，刘娟妮

(1.西北工业大学计算机学院，西安 710129;2.空间微波技术国家级重点实验室，西安 710100)

0 引 言

近年来人工智能技术，尤其是深度学习技术取得了突破性进展，在多个任务上均取得了最优性能。相比于传统技术，深度学习技术在性能上有巨大优势，众多学者尝试将该技术应用到目标检测[1]和识别、异常检测[2]、变化检测[3]、对地观测[4]等空间任务中。相关研究成果表明深度学习技术性能优异，在空间任务中具有广阔的应用前景。

遥感图像目标检测是遥感图像处理的基本任务之一，也是遥感图像分析、图像理解和场景理解等高级应用的基础。但受空间环境限制，星上计算能力和存储能力与地面相差甚远，而且深度学习算法是计算密集型和存储密集型算法，其优异的性能是以大量计算资源和存储资源消耗为代价。在星上部署基于深度学习的目标检测算法比地面上更具有挑战性，因此，目标检测算法在轨加速技术是一个重要研究领域，同时也是研究热点和难点。

在星上实现深度学习算法加速主要涉及加速器硬件平台、算法模型以及计算引擎三个方面。

加速器硬件平台主要有图形处理器(GPU)、中央处理器(CPU)以及现场可编程门阵列(FPGA)。当前地面深度学习算法加速以GPU为主，尽管GPU计算性能强劲，但其功耗动辄百瓦以上，能效比较低；CPU能效相对GPU较高，但其计算能力有限，因此GPU及CPU均无法满足在轨应用需求。

随着深度学习算法在地面上不断深入应用，诸如Nvidia Jetson系列GPU及Myriad 2视觉处理器(VPU)等高能效比加速器也随之产生。此类加速器配套和生态也较为成熟，可很好应用于地面移动场景。但此类加速器并非针对空间环境设计，在空间应用时，会因空间环境的单粒子效应造成加速器发生单粒子翻转[5]，导致算法性能急剧下降甚至造成加速器永久损坏。因此，需要选用适合空间环境的硬件平台来实现深度学习算法的加速。

FPGA在传统星上处理中应用广泛，具有应对空间环境的成熟方法。此外，FPGA具有可编程特点，在模型和算法开发过程中可以不断改进和完善，甚至可以实现在轨重构。文献[6-7]表明ESA Φ-Sat-1卫星采用Myriad 2 VPU实现在轨智能云检测，但由于其可靠性问题，在后续任务中已经采用FPGA作为在轨加速器件。鉴于FPGA的高可靠性、在轨重构能力以及强大的处理能力，将FPGA作为星载深度学习算法加速硬件平台是一个可行的方案。

在加速器所实现的算法模型方面，学者们对此进行了广泛研究[8-10]，但基于FPGA的加速器设计与最新算法模型之间仍有较大差距[11]。有一部分FPGA加速器是针对AlexNet[12],VGG16[13],ResNet[14]等模型所设计，此类模型参数量大，消耗大量计算资源和存储资源，难以在星上部署。

有一部分FPGA加速器是针对轻量化模型所设计[15-17]，此类模型参数量少，消耗的计算量也小。此类加速器所消耗的硬件资源和功耗相对通用大模型具有较大优势，适合在星上进行部署。

针对目标检测算法在轨应用需求，在前期工作中将轻量化思想引入遥感图像目标检测，提出了一种轻量化遥感图像目标检测算法MSF-SNET[18]。该算法参数量仅有1.54 M，计算量仅有0.21 GFLOPs(每秒千兆次浮点运算)，适合在星上部署。针对特定算法设计特定加速器，可以有效提高资源利用率，是未来FPGA加速器发展的一个重要方向。

在加速器设计与实现方面，根据加速器的结构大致可以分为两大类，一类是流水线结构[16]，另外一类是统一处理结构[15,19]。

流水线结构的优点是流水线上的每一个卷积层并行处理，有利于提高加速器性能。该结构的缺点是其硬件开销较大，每一个卷积层都需要独立的处理单元，每一个处理单元也只能处理与其对应的卷积层，从而造成了硬件资源开销大，利用率低。因此，流水线结构只适合用来实现层数较少且结构单一的卷积网络加速。

统一处理结构的优点是能够大幅降低硬件资源消耗，能够在有限的硬件资源上实现任意层数的CNN加速，硬件资源利用率较高。该结构的缺点是需要不断从外部DDR中读取输入特征图到片上缓存，因而加速器需要有足够的外部存储器带宽，且增加了数据从外部存储器进入加速器的时延以及不断读写外部缓存造成功耗的增加。

在空间环境中能够提供的硬件资源有限，且MSF-SNET轻量化算法具有分支网络，在星上采用统一处理结构具有可行性。

无论流水线结构还是统一处理结构，都需要计算引擎来完成CNN中的运算。计算引擎按照其实现方式可以分为GEMM[19](General matrix multiplic-ations),WT[20](Winograd transform),FFT[21](Fast Fourier transform)以及乘累加树[22-23]。

GEMM的基本思想是将3维卷积转换成两个矩阵相乘。其优点是通用性强，CPU、GPU以及Intel的OpenCL均采用该方法实现加速，缺点是矩阵相乘会在输入特征图中引入冗余数据，从而造成硬件资源利用率降低，计算效率下降[24]。

WT方法同样是将卷积转换为矩阵相乘进行运算。其优点是可以有效减少计算量，缺点是需要设计不同的变换矩阵来应对不同大小的卷积核，在FPGA中实现矩阵乘法需要消耗大量的存储资源。

FFT方法是将卷积从空域转换到频域进行计算，文献[25]指出FFT方法在卷积核尺寸大于5时计算效率较高，在卷积核尺寸较小时并无优势。

乘累加树在FPGA加速器中使用较多，该方法通过给卷积核的每一元素设计一个乘法器，然后使用累加树将乘积累加起来从而实现卷积运算，其优点是计算效率高且实现方便简单，缺点是针对不同的卷积算子需要设计不同的计算引擎。

虽然文献中对基于FPGA的CNN网络加速技术进行了广泛研究，但在轻量化目标检测加速中仍然存在挑战。主要体现在轻量化网络中往往同时涉及到多种卷积算子，例如ShuffleNet V2以及Mobi-leNetsV2中均涉及到普通3×3卷积和深度可分离卷积，MSF-SNET涉及到了普通3×3卷积、3×3空洞深度可分离卷积和1×1卷积三种卷积算子。目前主流做法是通过GEMM方法或者在加速器中设计多种计算引擎来实现CNN中多种卷积算子的计算。文献[15]针对MobileNets中涉及到的普通3×3卷积和深度可分离卷积分别设计了两种不同计算引擎，在CNN中卷积逐层计算，不同计算引擎难以同时利用从而造成了硬件资源利用低，计算效率下降。

本文针对轻量化目标检测算法MSF-SNET在轨部署需求，提出了一种在轨目标检测算法加速框架以及一种能够兼容三种卷积算子的计算引擎，解决了目前轻量化算法FPGA加速中面临的硬件资源利用低和计算效率低的问题，实现了轻量化目标检测算法MSF-SNET在轨加速。

1 算法优化

1.1 MSF-SNET算法时空复杂度分析

MSF-SNET算法的骨干网主要由如图1(a)所示的BU(Basic building unit)和图1(b)所示的SDU(Spatial down sampling(2x) unit)组成。涉及到3×3卷积、1×1卷积及3×3空洞深度可分离卷积。

图1 骨干网组成模块Fig.1 Building blocks of MSF-SNET

当输入特征图X的通道数为C，高和宽分别为H和W，采用输入通道数为C、输出通道数为T的3×3卷积核K进行卷积时，输出特征图Y为式(1)所示，其尺寸为T×H×W。

(1)

卷积运算占用的存储空间Msc和消耗的计算量Jsc分别为式(2)和式(3)所示。

Msc=T×C×D2×Nb

(2)

Jsc=(2×C×T×D2)×H×W

(3)

式中：D表示标准卷积核尺寸；Nb表示每个参数量化的比特数。

当采用3×3空洞深度可分离卷积算子对输入特征图X进行卷积时其输出特征图Y为式(4)所示。

(4)

其占用的存储空间Mdsc和消耗的计算量Jdsc分别表示为式(5)和式(6)。

Mdsc=C×D2×Nb

(5)

Jdsc=(C×D2×H×W)/2

(6)

当采用1×1卷积对输入特征图X进行卷积时，其输出特征图Y为式(7)所示。

(7)

其占用的存储空间MPSC和消耗的计算量Jpsc分别表示为式(8)和式(9)。

Mpsc=C×D2×Nb

(8)

Jpsc=(C×D2×H×W)/2

(9)

1.2 卷积并行化

为了高效完成MSF-SNET算法中多种卷积算子运算，需要将算法并行化。由于卷积核之间相互独立，卷积核各个通道之间相互独立，通道内各个元素之间的运算相互独立，因此可以在通道和卷积核两个维度将其展开，并在通道内采用乘累加树的思想实现算法的并行化。

若通道并行度为C，在设计加速引擎时，采用C个并行计算单元实现并行运算。如果卷积核并行度为N，则采用N个加速引擎实现卷积核并行运算。

在卷积运算中输入特征图是一个3维张量，其通道数为Nin，宽和高分别为W和H，卷积核是一个4维张量，其中卷积核数目为Nout，其通道数、宽和高与输入特征图对应参数相同。由于FPGA片上资源有限，并不能够将算法完全并行化，因此需要在通道和卷积核两个维度上进行切片。并行化后第q层卷积运算所消耗的时间如式(10)所示，所有卷积层消耗时间如式(11)所示。

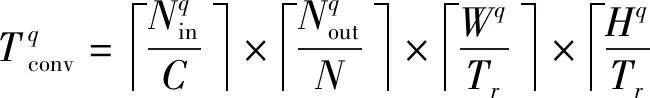
(10)

(11)

式中：Tr表示输入特征图宽和高的分割因子；Nreused是行数据复用因子Nreused_r和列复用因子Nreused_c之积。

从式(10)和式(11)可以看出算法所消耗的时间与并行度C和N成反比，受片上计算资源限制，C和N需要受式(12)约束。

N×C×NC_DSP≤αNDSP

(12)

式中：NC_DSP为单个通道卷积计算所消耗的计算资源数量；NDSP为片上计算资源总数；α为经验因子，一般情况下该值取0.7为宜。

1.3 批归一化层优化

为了提高计算引擎效率，减少硬件资源消耗，将批归一化运算融合到卷积层中。在训练过程中，批归一化可以用式(13)和式(14)表示，其中μ和σ2为均值和方差。

(13)

(14)

(15)

(16)

Y=X*W+B

(17)

Y=X*W′+B′

(18)

在训练结束后超参数γ和β以及统计参数均值和方差已经确定，模型中的权重和偏置可以分别表示为式(15)和式(16)。因此，式(17)所示的卷积运算可以融合为式(18)所示的运算。在加速器中无需再单独设计批归一化处理单元。

2 MSF-SNET算法FPGA加速器

2.1 加速器框架

加速总体框架如图2所示，主要包含控制模块、缓存模块和计算模块三大部分。缓存模块用于临时存储模型权重、输入特征图和输出特征图。片上缓存容量有限，无法将模型所有参数及输入特征图缓存在片上RAM中，需要将模型参数和输入特征图分割成运算数据单元逐次加载。

图2 MSF-SNET算法加速总体框架Fig.2 The overall structure of accelerator for MSF-SNET algorithm

在运算时通过数据总线将输入特征图和模型权重从片上缓存器加载到计算单元。在运算结束后通过数据总线将计算结果写入片上缓存。

计算模块负责完成MSF-SNET算法中涉及到的所有运算。计算模块由多个功能相同的计算引擎组成，完成卷积核维度的并行计算，其数量为N，每个计算引擎中含有16 bit定点运算资源，完成基本的乘累加及比较运算。各个计算引擎之间通过数据总线和控制总线相连。根据FPGA可提供的计算资源灵活增加或者减少计算引擎数量，各个计算引擎并行完成所分配的计算任务。

由1.2节分析可知，计算单元的通道并行度为C，卷积核并行度为N，每个时钟周期加速器可以处理N个卷积核的C个通道，因此在加速器启动后将N个卷积核的C个参数从外部DDR3加载到权值缓存中，然后将切片后的输入特征图从外部DDR3中加载到输入特征缓存。当输入特征图和权值参数准备就绪之后，将二者同时加载到计算单元完成相应运算。以此方式完成卷积层中卷积核所有通道运算，并通过输入特征缓存将计算结果写入外部DDR3。

2.2 并行计算引擎

深度卷积网络模型参数通常采用32 bit全精度浮点数表示，但FPGA并不擅长处理浮点型数据。为了在FPGA上实现该算法，在通道间采用动态量化策略，在通道内采用静态量化策略将32 bit全精度浮点数模型参数转换为16比特定点模型参数。

计算引擎需要完成MSF-SNET目标检测算法中所包含的1×1卷积、3×3卷积、3×3可分离空洞卷积、ReLU激活、maxpool等功能。为了实现不同卷积算子，文献[16]针对不同算子设计了不同计算单元，由于同一时刻并非所有算子都参与运算，这种设计方法大大降低了计算资源利用率。为了提高计算引擎的效率及利用率，本文提出了一种3维立体计算引擎，实现了在同一计算单元中兼容1×1卷积、3×3卷积及3×3可分离空洞卷积三种卷积算子，有效提高了资源利用率。

如图3所示，3维立体计算引擎由多个计算单元堆叠形成，其数量为C。每个计算单元均能够独立完成三种卷积算子运算、激活及池化运算。计算引擎并行完成C个通道的运算，这种设计具有很高的灵活性，可以根据FPGA片上资源以及加速器的性能需求来选择合适的计算单元数量。每个计算单元中包含9个乘法器、9个加法器、9个寄存器、后处理单元以及ReLU模块。

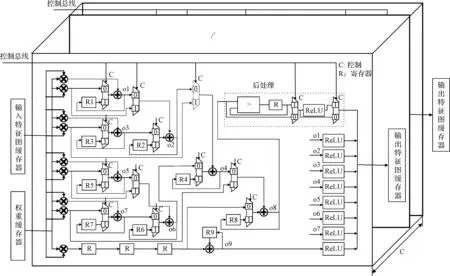
图3 三维立体计算引擎Fig.3 3D computing engine

对于标准3×3卷积，每个通道需要进行9次乘法运算并将其结果累加。输入特征图缓存器输入一个通道的数据，权重缓存器中输入卷积核的一个通道的参数。采用9个乘法器完成卷积中的乘法运算，之后通过选择器将9个加法器组成一个加法树，以流水线方式实现乘累加。卷积结果写入寄存器R9中，多个通道的卷积结果通过加法器累加到一起。再将同一计算引擎中的多个计算单元的计算结果累加即实现了一个卷积核的一次卷积运算。

3×3可分离空洞卷积与标准3×3卷积的计算过程相同，但输入特征图和卷积核不同。标准卷积一次输入3×3的特征图，空洞卷积则需要输入5×5的特征图；标准卷积每个卷积核有多个通道，而空洞卷积每个卷积核仅有一个通道。由于二者计算过程一致，在输入特征图进入缓存时，将空洞去除，从而使得同一计算单元能够计算空洞卷积。

对于1×1卷积，每个通道仅需要一次乘法运算，然后将多个通道的乘积累加。为了充分利用计算单元中的运算资源，通过选择器将计算单元中的9个乘法器和9个加法器配置为可以独立运算的卷积运算单元。此时，输入特征图缓存器输入一个通道的数据，权重缓存器输入9个卷积核，在一个计算单元中可并行完成9个卷积核运算。

图4 最大池化单元Fig.4 Maxpooling unit

MSF-SNET算法在第一层卷积之后需要进行一次3×3最大池化。通常卷积计算采用逐行滑动方法，这种卷积计算方法需要采用line buffer组成池化窗口[15]。为了减少池化所消耗的存储资源，本文利用卷积计算顺序形成池化窗口。卷积运算顺序按照局部Z形滑动，即在卷积计算过程中先水平滑动3次，然后垂直滑动1次，以此类推，完成9个卷积窗口计算后便会形成一个3×3的池化窗口。从而避免因使用line buffer造成的资源消耗。

最大池化单元设计如图4所示。池化运算单元输入为3×3卷积运算结果。两个控制信号分别为是否是池化层及是否需要进行激活。寄存器R用来存储当前最大值，如果是池化层，则将寄存器中存储的最大值与当前卷积结果进行比较，并更新寄存器。当9个卷积窗口均完成之后得到最大值。

2.3 数据组织与缓存设计

为降低频繁访问外部缓存带来的数据传输时延和功耗，需要设置片内特征图缓存和模型参数缓存。

模型参数缓存设计如图5所示，加速器中N个计算引擎同步并行运行，针对各计算引擎设计独立缓存器WB(Weight Buffer)，从而实现模型参数到计算引擎的同步加载。每个计算引擎中又包含了C个独立计算单元，每个计算单元可独立完成一次3×3卷积或9次1×1卷积。在WB中设置C个独立BR(Block RAM)，分别用来缓存每个计算单元所需要的参数。BR位宽为9个16位字(144 bit)，深度为2×Mi，其中Mi为单次加载的输入特征图的通道数。每个地址存储1个3×3×Mi卷积核中一个通道的参数或者9个1×1卷积核中一个通道的参数。

计算3×3卷积时每个WB中缓存1个卷积核。卷积核按照通道均匀存储在不同BR中，每个地址存储一个通道。例如，在C=16，Mi=32时，对于3×3×512的卷积核，第0至31通道按照顺序缓存在BR(0)中，第32至第63通道缓存在BR(1)中，以此类推，第480通道至511通道缓存在BR(15)中。每个时钟周期每个计算单元从其对应的BR中加载一个卷积核的一个通道进行运算。Mi个时钟周期便可以完成一个卷积核的运算。

图5 模型参数缓存设计Fig.5 Weight buffer organization

1×1卷积核在缓存中的组织如图6所示。每个WB中缓存9个卷积核，9个卷积核并列存储，同样按照通道均匀存储在不同BR中，每个地址并列存储9个卷积核的一个通道。例如，9个1×1×512的卷积核的第0通道并列存储在BR(0)中的0地址上。其中第0比特至第15比特为Filter0第一通道的参数，第16比特至第31比特为Filter1第一通道的参数，以此类推，在第128比特至第143比特为Filter8第一通道参数。每个时钟周期每个计算单元可以从其对应BR中加载9个卷积核的一个通道进行运算。Mi个时钟周期便可以完成9个卷积核运算。

图6 1×1卷积核参数缓存设计Fig.6 1×1 convolution weight buffer organization

受FPGA内部BRAM资源限制，无法将特征图中所有数据加载到片上缓存，因此需要将特征图进行分块后逐块加载。为了适配算法中3×3空洞卷积，特征图按照5×5×Mi大小的数据块进行加载，其中Mi为所加载的输入特征图的通道数。

如图7所示，加速器中共设置4个数据缓冲器DB(Data Buffer)，每个DB缓存容量与特征图数据块大小一致。将DB0和DB1组成一个乒乓缓冲器，DB2和DB3组成另外一个乒乓缓冲器，从而使得加速器能够连续将数据送入计算引擎进行计算。在使用DB0中的数据时将第2块数据预加载到DB1中。在使用DB1中的数据时将第3块数据加载到DB0中，以此类推循环使用两个数据缓存器。

每个DB由5个独立的子缓存器组成，每个子缓存器用来存储数据块一行中所有通道的数据。从子缓存器中读出的数据共享给所有计算引擎，并与不同的卷积核进行卷积。从图中可以看出每个子缓存器设计为三维立体缓存形式，其存储位宽为5个字，深度为Mi，高度为N，其中N为计算引擎中计算单元数目。数据块的一行中Mi个通道所有数据按照通道均匀存储在子缓存器中。在一个时钟周期内可以并行读出N个通道的数据。

由于5个子缓存器中分别存储了5行特征图，在卷积计算过程中，分别从不同的子缓存器中读出特征图数据即可以组成一个卷积窗口。

图7 输入特征图缓存设计Fig.7 Input feature map buffer organization

2.4 加速器性能分析

文献[10]引入了针对FPGA的Roofline模型用于评估算法与加速器之间的匹配程度。本文采用该模型对所设计的加速器进行定量分析。

加速器性能PATP为

PATP=min(PPE×S,IC×BW)

(19)

式中：PPE为单个计算单元的峰值性能(GFLOPS)。

式(19)中S为可扩展因子，表示为

(20)

式中：AR表示FPGA中可用资源；RCPE表示每个计算单元所消耗的资源。

IC计算强度，定义为每字节外部DRAM数据流所能支撑的计算量(FLOPS/Byte)，该参数与算法相关，代表了加速器所需要的带宽。BW表示加速器可以提供的带宽。

根据FPGA的Roofline模型中各个参数的定义可知，在本算法中PPE为

PPE=F×NBPW×NWOPK

(21)

式中：F表示计算单元运行频率；NBPW表示运算字的字节数目，本设计中运算字节数为2；NWOPK表示单个计算单元所能完成的运算量，本设计中一个时钟周期内完成乘法和加法运算各9次。

根据可扩展因子的定义，S可表示为

(22)

式中各项分子表示FPGA中所包含的LUT，FF，DSP，BRAM资源，分母为单个计算单元所消耗的FPGA资源。

计算强度为一个数据复用周期内总计算量与数据读写总量的比值，表示为

(23)

将运算中各个参数代入式(23)之后，计算强度IC表示为

(24)

式中：Nreused_r为行数据复用因子；Nreused_c为列数据复用因子；NPE为同一复用数据通道计算单元数目；Nread为数据复用周期内从外部DRAM中读取数据的次数；Ndata为单次读取的数据量；No为单个数据复用周期内需要向外部DARM写入的数据量。三种卷积算子参数及计算强度如表1所示。

表1 三种卷积算子参数及计算强度Table 1 Computational intensity and parameters for three convolution operators

BW为运算平台所具有的外部DRAM带宽，本文所设计的平台外部挂8片DDR3，总数据位宽为256 bit，数据总线频率为800 MHz，按照80%的效率计算，DDR带宽为40.96 GB。从roofline模型可知，可扩展因子S、时钟频率F以及外部DRAM带宽BW是影响加速器性能的主要因素，其中F和S确定了加速器算力上限，BW确定了加速器带宽上限。

当BW确定时，加速器的带宽上限确定。由式(19)可知其带宽瓶颈IC×BW为2589.01GFLOPs。此时，增加时钟频率F和可扩展因子S均会提高加速器的计算性能，但前者会消耗FPGA中的布线资源，后者会消耗FPGA中的计算资源。当时钟频率为100 MHz时，S是影响加速器的主要因素。例如，当S为128时，其计算性能为460.8GFLOPs，当S增加到256时，其计算性能提升到了921.6GFLOPs。当S确定时，提高时钟频率会提升加速器的性能，例如，在S为256时，将时钟频率从100 MHz提高到200 MHz时，其计算性能从921.6GFLOPs提升到1843.2GFLOPs。但是时钟频率超过200 MHz之后FPGA布线难度增大，甚至会造成布线失败。

在时钟频率F和可扩展因子S确定，即加速器所消耗的资源确定的情况下，外部BRAM的带宽BW是影响加速器性能的主要因素。例如，当时钟频率为200 MHz，S为256时，由式(21)可知，其计算性能的瓶颈PPE×S为1843.2GFLOPs。当DDR芯片从8片减少到4片时，加速器的计算性能IC×BW为1294.54 GFLOPs，由此可见，由于DDR带宽不足造成了加速器性能由1843.2GFLOPs下降到了1294.54 GFLOPs，损失了29.76%。

3 仿真校验

本文中使用Verilog硬件描述语言在Xilinx XC7VX690T,XC7K480T,XC7A200T,XC7Z045四种FPGA上实现了该加速器，并对不同FPGA平台上加速器的性能进行评估，通过峰值性能、功耗及推理时间三个指标对加速器进行评价。加速器设计采用了Xilinx VIVADO2019.2，加速器功耗采用Xilinx功耗分析工具获得。

3.1 加速器性能评估

本文加速器在不同FPGA上的资源占用情况如表2所示。当N=16，C=16时，此时扩展因子S为256，可以在XC7VX690T上实现该加速器。DSP消耗达到64%，BRAM资源消耗达到69.80%，LUT和FF资源消耗分别为21.32%和21.15%。

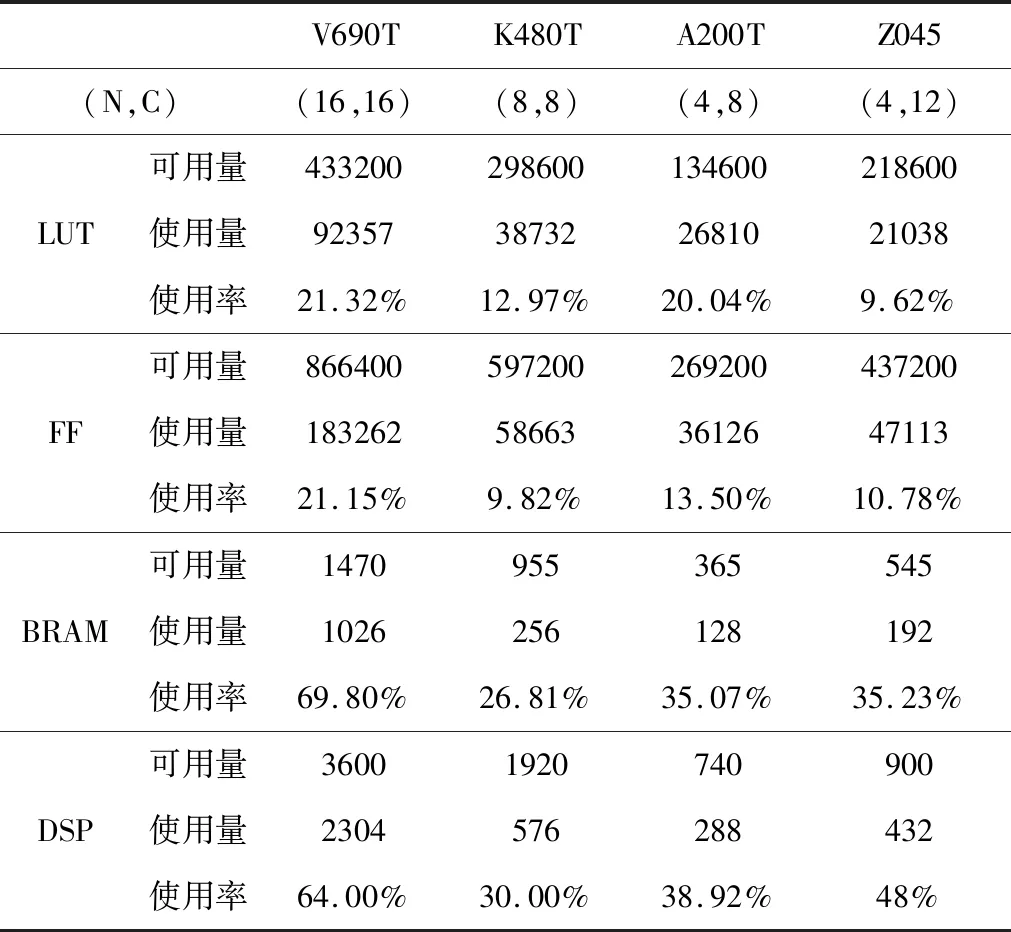
表2 加速器在不同FPGA上的资源消耗情况Table 2 Utilization of the accelerator on different FPGA

可见，DSP资源和BRAM资源是限制加速器规模和性能的主要因素。时钟频率改变不影响DSP资源和BRAM资源的消耗，对FF资源和LUT资源的消耗稍有不同。当N和C参数均为8时，可将该加速器适配到Xilinx中端FPGA XC7K480T上，当N和C参数分别为4和8时，可以将该加速器适配到低端平台XC7A200T上，当N和C参数分别为4和12时，可以将该加速器适配到Xilinx嵌入式平台XC7Z045上。可见，该框架具有良好的扩展性，可以根据需求部署到不同FPGA上。

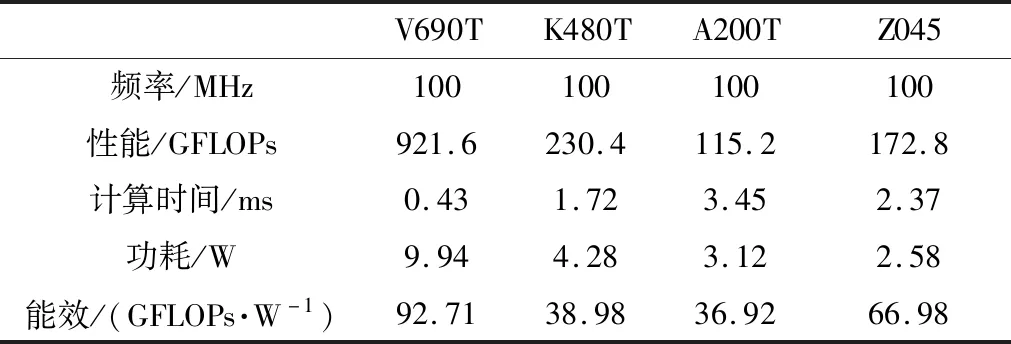
表3 加速器在不同FPGA上的性能(100 MHz)Table 3 Performance of the accelerator on different FPGA (100 MHz)

当频率为100 MHz时，加速器在不同FPGA上的性能如表3所示。由于XC7VX690T的DSP资源和BRAM资源最多，其可扩展因子S最大，在相同的时钟频率下加速器可以达到最高性能和最大能效比。此时，加速器计算性能为921.6GFLOPs，功耗为9.94 W，能效比为92.71，推理时间为0.43 ms。四种FPGA平台中XC7A200T资源最少，其可扩展因子S最高仅为32，此时加速器性能为115.2GFLOPs。可见，在相同时钟频率下，不同FPGA平台上可扩展因子不同，所能达到的性能也不同。

当频率为150 MHz时，加速器在不同FPGA上的性能如表4所示。由于频率提高了50%，加速器在XC7VX690T上的计算性能提高了50%，达到了1382.4GFLOPs，推理时间也缩短到了0.29 ms，但功耗增加了3.17 W。在其它三种FPGA平台上加速器的性能也相应提高了50%，功耗也有所增加。可见，频率是影响加速器性能的关键因素，提高频率，可以提高加速器性能，但其功耗也会增加。

表4 加速器在不同FPGA上的性能(150 MHz)Table 4 Performance of the accelerator on different FPGA (150 MHz)

当时钟频率为200 MHz时，加速器在不同FPGA上的性能如表5所示。当频率进一步增加，加速器在XC7VX690T上性能达到了1843.2GFLOPs，功耗也增加到了16.32 W，能效比为112.94。

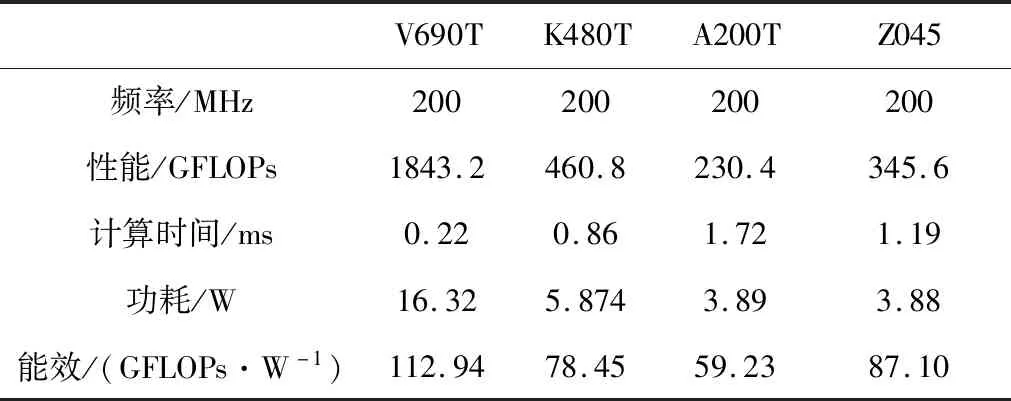
表5 加速器在不同FPGA上的性能(200 MHz)Table 5 Performance of the accelerator on different FPGA (200 MHz)

显然，在加速器带宽和FPGA平台确定的情况下，可以通过提高时钟频率来提高加速器性能，但是，当频率提高到某一个值时，进一步提高时钟频率会使得布线失败。在本设计中，时钟频率超过200 MHz时，布线资源紧张。值得注意的是在时钟频率为200 MHz时也可以将本文加速器部署到Xilinx低端FPGA XC7A200T上。在功耗为3.88 W时可以达到230.4GFLOPs的计算性能，对于256×256×3的图像推理时间只需要1.72 ms。

3.2 性能对比

由于不同FPGA的资源以及采用的工艺不同，加速器能达到的规模和性能也不同。为了实现公平对比，本文分别在Xilinx Virtex-7系列FPGA,Xilinx Z系列FPGA和Intel FPGA上进行了对比。Virtex系列FPGA是空间应用的主流器件，本文将所提出的加速器分别在100 MHz,150 MHz和200 MHz时与其它性能较好的加速器进行对比。

表6 与其它加速器性能对比(100 MHz)Table 6 Performance comparison with other accelerators (100 MHz)

表6显示了在Virtex-7系列FPGA上频率为100 MHz时本文所提加速器与其它加速器性能对比结果。文献[27]与本文均采用了XC7VX690T，虽然文献[23,26]采用了XC7VX485T，但属于同一系列，具有可比性。此时，本文加速器计算性能为921.6GFLOPS，是文献[27]加速器的2.07倍，是文献[23]加速器的14.96倍。本文加速器功耗为9.94 W，是文献[27]加速器功耗的38.2%，是文献[23]加速器功耗的53%。本文所提出加速器能效比达到了92.71，是文献[23]中加速器能效比的28倍，是文献[27]中加速器能效比的5.16倍。由于本文采用了轻量化网络，计算时间为0.43 ms，是文献[27]推理时间的12.75%。可见，在100 MHz时，本文加速器在计算性能、计算时间以及能效比方面具有优势。

表7显示了频率为150 MHz时本文提出的加速器与其它加速器的性能对比。可以看出文献[13,28]中加速器频率为150 MHz，文献[12]中加速器频率为156 MHz。由于本文计算引擎中实现了三种卷积算子的有机融合，从而大大提高了FPGA中DSP资源的利用率，在150 MHz频率下，性能达到了1382.4GFLOPs，是文献[12]加速器性能的2.44倍，是文献[13]加速器性能的6.78倍，是文献[28]加速器的2.17倍。由于本文采用了轻量化模型，推理时间具有极大优势，仅0.29 ms即可完成一幅图像推理，而文献[13]中的加速器采用了VGG网络，推理时间高达151.8 ms。在能效方面，本文加速器能效是文献[13]加速器的18.08倍，是文献[12]加速器的4.76倍。

表7 与其它加速器性能对比(150 MHz)Table 7 Performance comparison with other accelerators (150 MHz)

表8显示了频率为200 MHz时本文加速器与其它加速器的性能对比。表中TY3代表Tiny YOLO V3，Y2代表YOLO V2，RS18代表ResNet-18。在相同时钟频率下本文加速器计算性能与文献[16]所提加速器的计算性能相当，在功耗和能效比方面有一定优势。但是在推理时间上文献[16]消耗时间是本文所提方案的41.59倍。本文加速器在性能、推理时间和能耗方面远超文献[14,17]中的加速器。

表8 与其它加速器性能对比(200 MHz)Table 8 Performance comparison with other accelerators (200 MHz)

表9显示了本文提出的加速器在Xilinx Z系列FPGA上与其它加速器的性能对比。文献[29]中加速器的时钟频率为150 MHz，文献[30-31]中加速器时钟频率分别为167 MHz和142 MHz。本文加速器计算性能方面略优于文献[30-31]中加速器计算性能，是文献[29]中加速器计算性能的1.89倍。本文加速器功耗为1.58 W，是文献[29]中加速器功耗的35.5%，是文献[31]的80%。本文加速器能效比为81，是文献[29]中加速器能效比的5.7倍，是文献[31]中加速器能效比的1.43倍。可见，在Xilinx Z系列FPGA上，本文加速器性能优于同类加速器性能。

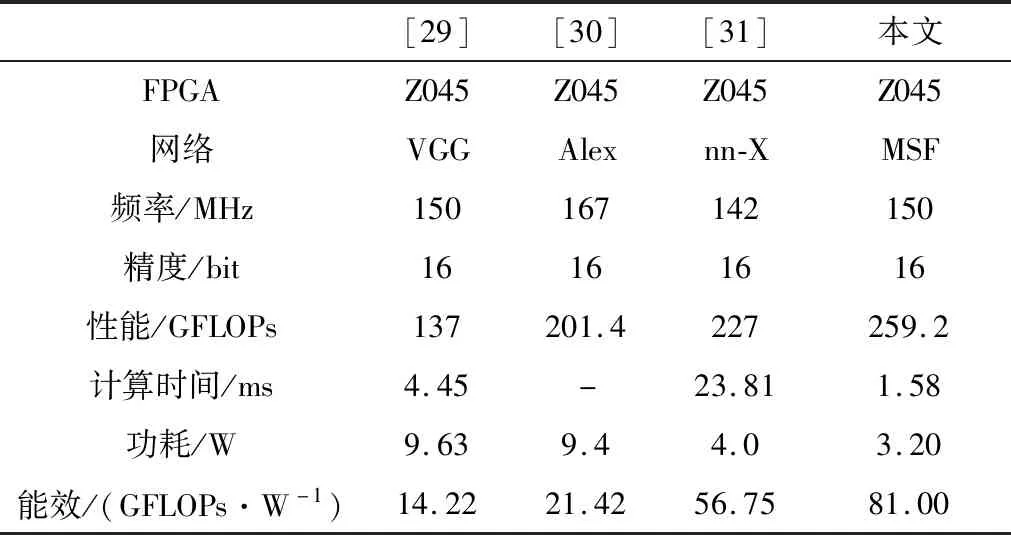
表9 在Xilinx Z系列FPGA上与其它加速器性能对比Table 9 Performance comparison with other accelerators on Xilinx Z series FPGA

4 结 论

本文提出了一种在轨高效目标检测加速器框架，并在Xilinx多款FPGA上实现了该加速器。所提出的计算引擎设计方法实现了三种卷积算子的有机融合，使得目标检测算法与硬件加速器更好的匹配，达到最优性能和最高能效比。

通过在多款FPGA及多种时钟频率下对该加速器的性能评估我们可以得出以下结论：

1) 与同类加速器方案相比，本文所提出的加速器框架在性能、功耗、能效比及计算时间方面具有优势，适合部署在资源受限环境中，具有良好的星上应用前景和价值；

2) 通过在Xilinx XC7VX690T,XC7K480T,XC7A200T,XC7Z045 FPGA上的验证表明该框架具有良好的可扩展性和适配性，可以根据性能、功耗、推理时间及成本要求将其部署到不同FPGA上；

3) 虽然本文提出的目标检测算法加速框架是针对MSF-SNET算法所做的加速，但该加速框架可以推广应用到其它算法的加速中。

综上所述，本文所提出的加速器框架具有良好的性能，不仅具有理论价值也具有工程借鉴意义。此外，该加速框架针对目标检测算法设计，下一步可以将其推广到其它算法。