面向GEO目标的快速在线在轨服务任务规划
徐 杭,梁维奎,,刘鲁江,马广富,宋 斌
(1.哈尔滨工业大学航天学院控制科学与工程系,哈尔滨 150001;2.上海宇航系统工程研究所,上海 201109)
0 引 言
空间设备在轨运行时环境复杂多变,不可避免出现各种损耗,因此往往具有高风险、长期使用、高投入等特征。根据UCS卫星数据库统计[1],截至2021年12月31日,在地球同步轨道(GEO)上已有574颗卫星,包括通信卫星等高价值空间设备。除此以外,还有大量无法观测到的空间碎片也分布在该区域。与近地轨道(LEO)不同,GEO报废卫星不会飞回大气层销毁,根据欧洲航天局的年度调查报告,2017年19颗大型静止轨道卫星在服役期满后被送入更高的坟墓轨道,这些报废卫星与空间碎片一旦发生碰撞将严重威胁GEO卫星的正常运行,带来灾难性影响[2]。因此为了延长空间设备的使用寿命、保障空间设备的稳定运行、提升工作性能,需要使用空间在轨服务(On-orbit servicing,OOS),为各类航天器提供燃料加注、功能维护、模块升级等辅助保障服务,同时及时纾解太空垃圾,减少空间碎片对在轨卫星的碰撞风险。随着技术水平的不断进步,中国在该方向已经积累了不少经验。2016年中国成功发射天源一号卫星实现首次卫星“空中加油”,相继又实现了天舟一号对天宫二号的推进剂补加、实践二十一号对太空垃圾的抓捕。随着人类发射卫星数量的增多和在轨服务技术的日渐成熟,在可预见的未来在轨服务技术将得到大规模的应用。而在实现在轨服务的过程中,多个航天器对多个目标进行任务规划是任务实施的重要一环,本文针对GEO多对多在轨服务任务规划进行分析。
目前国内外对于航天器多对多的在轨服务任务规划已经开展了大量的研究。吴钰飞等[3]建立了面向地球静止轨道航天器的合同网协议多agent模型,任务紧急程度近似为目标函数时间燃料权重比,但其任务分配过程中只是确定哪个航天器去服务哪个单目标。张进等[4]提出了一种混合编码遗传算法来求解近地轨道的多航天器加油模型,模型中考虑了J2摄动影响和时间窗约束,并使用相对动力学方程来求解转移过程。赵凡宇等[5]提出了基于规划活动相关度的领域无关启发式规划方法,明显减少了规划步数与回溯步数。欧阳琦等[6]以地球同步轨道卫星群为对象,基于遗传算法求解多对多在轨加注任务规划问题。陈小前等[7]比较了一对一策略、一对多策略、多对多策略、P2P策略的经济效率,提出了一种混合策略框架以实现更好的收益。余婧等[8]基于混杂优化控制理论对GEO在轨燃油加注过程提出了数学表征,其中变轨过程考虑霍曼变轨和调相机动的组合,优化模型考虑多目标粒子群算法进行求解。文献[9]中优化目标考虑任务的燃油与时间消耗,以Lambert变轨过程建立优化模型,并用多目标粒子群算法求解。Bang等[10]基于车辆路径规划模型对主动式碎片清除任务规划问题建模,考虑短时任务(一星期以下)采用Lambert变轨方式,利用升交点赤经漂移的三步变轨方式用于长时任务。郑红星等[11]针对一对多的在轨服务规划问题设计了基于霍曼转移、异面机动、Lambert转移的空间任意目标变轨流程,并使用遗传算法进行求解,计算出服务时序。
在上述的研究中,由于航天器的多对多在轨服务任务规划为一个典型的混合整数规划问题,通常为了寻找“最优”方案,使用优化算法进行多轮次的迭代求解,在求解过程存在算法复杂性高、效率低、运行时间长、收敛性差等问题。且由于星上资源有限,往往需要在地面站形成方案后进行上注,存在时延、反应不及时(存在测控时间窗口)的问题。针对于突发事件(大量碎片产生),多个航天器平台进行自主探测、分布式规划相较于传统方案有显著优势,并可以结合启发式策略应对任务过载问题[12]。由于航天领域的特殊性,航天器自主任务规划面对计算资源有限、及时性、环境不确定性、目标动态性、系统耦合性、资源约束的动态复杂性、动作时间连续性等难点[13-15]。综上所述,对于星上规划平台而言,除了支持分布式框架,快速性规划方案生成是一个重要指标。
与优化算法的多轮次迭代求解不同,拍卖算法作为一种快速的分配算法,可以在计算速度上体现出很大优势,目前在机器人、无人机、军事等多个领域上得到了广泛关注[16-19]。结合启发式策略和一对一变轨策略取优,可以实现短时快速的规划问题“次优”解获取,比传统的优化求解方式具有更好的时间效率和更灵活的架构。
综上,为增强航天器自身自主化、智能化程度,实现快速任务规划,得到多个航天器对多个任务的分配关系、执行顺序、机动窗口、脉冲速度指令,本文基于拍卖算法,并根据飞行器在轨服务任务规划问题求解的需求特点,提出了一套融入启发式目标优先级排序策略的任务规划求解算法,并与传统的遗传算法、模拟退火算法求解效果进行对比,验证了所提算法的有效性和快速性。
1 数学模型
针对GEO待服务卫星目标,相对于LEO部署方案(服务航天器初始在LEO上运行)、应急发射方案(有服务任务时,航天器从地面发射),将服务航天器部署在相同GEO时更加经济,响应速度更快[20]。本文基于上述在轨服务模式建立数学模型,并考虑到如下假设:
1)在轨服务过程简化
考虑到问题研究的通用性,本文并未限制在轨服务的具体样式,服务过程近似处理为接触式,且不考虑服务时太阳光照角的影响。变轨过程空间位置变化相对于航天器尺寸也极大,航天器执行服务任务时,与目标在空间中同位置、同速度。
2)多航天器与多任务目标轨道高度相近
本文分析对象为GEO航天器与目标,考虑到实际偏差,假设存在高度差但较小。
3)多航天器与多任务目标轨道面相近
GEO上1°的轨道面倾角调整约需速度增量54 m/s,考虑到不同轨道面间的变轨调整燃料消耗极大,实际任务中考虑不会频繁得修正轨道面与轨道面之间的夹角。本文考虑所有航天器与目标轨道面夹角很小。超出范围的其余轨道面的服务航天器、任务目标可视为另一组独立规划。
4)圆轨道近似
多数GEO卫星偏心率都极小,本文考虑所有服务航天器与任务目标轨道为圆轨道。
5)地球碰撞不考虑
受航天器燃料约束,从GEO轨道上撞击地球需要耗费大量速度增量,分析时不必判断碰撞概率。
1.1 近轨高近共面圆轨道变轨策略
在航天器进行在轨服务时,需要与目标进行交会。作为多对多任务规划问题的重要子问题,一对一的单次轨道交会问题求解尤为重要。在通常任务规划问题求解中[20],往往采用异面交点变轨、霍曼变轨与调相机动完成与目标的相对轨道面调整、轨高调整、相位角调整,这些变轨方式在节约燃料消耗的同时放弃了变轨过程的快速性、灵活性。由于本文只对近轨高、近共面问题进行分析,选取变轨方式更为灵活的Lambert变轨,可以实现轨高、轨道面调整,且相比霍曼变轨、异面交点变轨不会有很大燃料消耗差距,调相机动视为一种特例考虑。构建变轨过程的二体运动模型如图1所示(近共面情况下的二维截面)。过程①中,针对相近轨高、近共面的服务目标,其初始位于C1处;服务航天器初始位于A处,采用多圈Lambert变轨方式进行轨道转移,在C2处与目标交会并进行在轨服务。
在转移轨道运行时,初末两点位置矢量为r1与r2,对应转移轨道速度为v1与v2,轨道转移过程运动时长为t,圈数为nr,Lambert变轨过程可表述为:
(v1,v2)=f(r1,r2,t,nr)
(1)
v1与v2的求解过程中[21],r1与r2矢量方向一致或相反时会导致无解,考虑当r1与r2相同时,可以采用调相轨道(视为Lambert变轨的一种特殊情况)进行补充,如图1中过程②所示,目标初始位于B处,当运动到A处时,航天器恰好通过调相轨道运动回A处。转移轨道初末速度可表述为:
(2)
式中:G表示万有引力常量;Me表示地球质量;r1表示转移轨道初末位置矢量模;aL表示椭圆转移轨道半长轴;h1表示转移前轨道面法向(和转移轨道、转移后轨道一致)。变轨前后位置矢量r1与r2、轨道速度v10,v20与变轨前后轨道的六要素φ1,φ2相关,可通过相关公式求解:
(v10,r1)=f(φ1)
(3)
(v20,r2)=f(φ2)
(4)
航天器在变轨后与目标交会视为相对静止,速度增量Δv为:
Δv=|v1-v10|+|v2-v20|
(5)

图1 Lambert变轨与调相机动Fig.1 Lambert transfer and phasing maneuver
为了确定一对一模式下的Lambert变轨策略,在六种不同工况下绘制变轨过程速度增量消耗与变轨时长关系曲线,工况参数如表1所示:

表1 六种不同工况Table 1 Six different conditions
服务航天器与目标偏心率均为零,对比结果如图2所示:
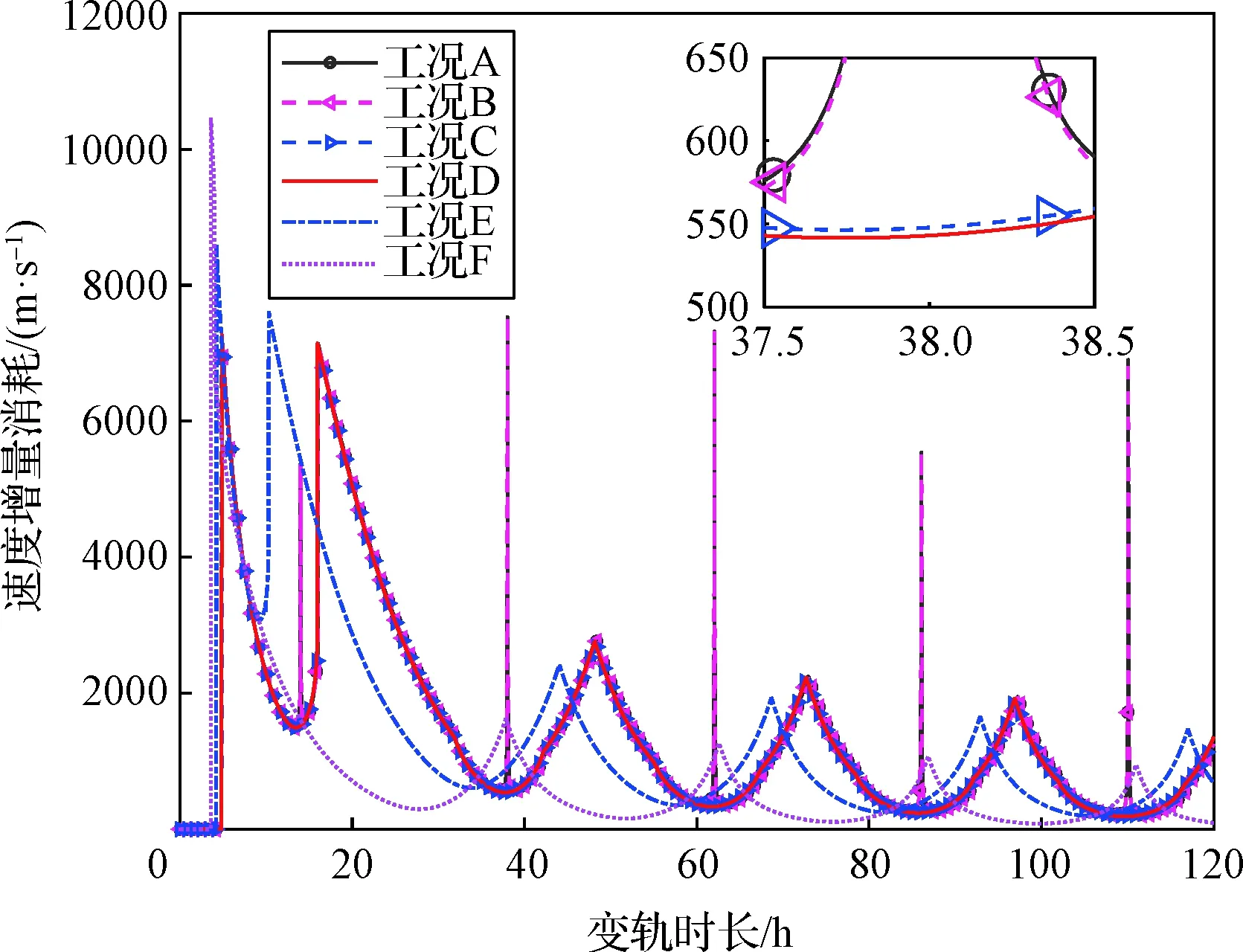
图2 速度增量与时长消耗图Fig.2 Relation between Δv and the consumption of time
可以从图2中得到几个结论:
1) Lambert变轨过程中存在周期性,整体变轨圈数越多、时间越长,速度增量消耗越小。
2) 当航天器与目标轨高相同时,每一个波谷对应调相轨道情况,速度增量消耗最小。
3) 当航天器与目标轨高不同时,会在近似相同轨高处理的对应调相轨道变轨时长处,速度增量消耗迅速增大,形成一前一后两个子波谷段。
4) 当航天器与目标存在轨道面夹角很小时,如图中工况A相对于B,工况C相对于D,产生的影响很小,不影响整体变化趋势。
5) 每一个波谷段前,近似变轨时间越长,速度增量消耗越小,大致呈递减趋势。
6) 当目标滞后相位角减小至60°时,第一个波谷段近似消失,此时单圈Lambert变轨近似至少消耗速度增量300 m/s。考虑受航天器燃料与任务时长约束,通常大相位角差时变轨超出了其自身能力,因此忽略目标相位角较大滞后情况下的第一个波谷,将第二个波谷视为第一个。
进一步分析,设置第一个波谷对应时长为T1:
(6)

TL 0=Tt 0-Ts
(7)
涉及到一个航天器对mi个目标服务时,一对一任务约束时长Tt 0由总时长约束T0平均分配:
(8)
当航天器与目标近轨高、近共面时,近似考虑在GEO上相对空间关系不会随着时间发生变化,不考虑光照情况下不存在时间窗口,因此本文中航天器在任务开始时立刻进行变轨,且在涉及对多个目标服务时不设置等待时间,前一个服务完立刻服务下一个。
同时考虑在给定的变轨时长约束下,尽可能得追求燃料最省。如果航天器与目标轨高相同,则可以直接取各波谷对应调相机动的变轨时长,然而实际中很难完全保持一致,因此需要变轨时长减去时间修正量Δt以对应到各波谷段的第一个子波谷(后一个子波谷段对应耗时更久不考虑)。
综上所述Lambert变轨过程时长t选取规则为:
(9)
式中:Δt表示时间修正量(和双方高度差及变轨时长有关);Tkmax表示可取的各波谷段第一个子波谷中时间最长的值(若共轨高没有子波谷则为波谷)。从上述也可以看出,针对每次一对一服务计算过程,本文策略仅需要数值求解一次Lambert变轨方程。
1.2 决策变量
设定在空间轨道部署有n个服务航天器,某时刻有m个目标卫星需要被执行相应的在轨服务,定义m个多维变量x:
x(i)=[ns,vL1,vL2,TL1,TL2,TL3],i=1,2,…,m
(10)
式中:x(i)表示每个目标对应的服务变量;ns表示服务航天器编号;vL1表示Lambert变轨第一次速度脉冲;vL2表示Lambert变轨第二次速度脉冲;TL1表示第一次变轨时刻;TL2表示第二次变轨时刻;TL3表示任务完成时刻。
1.3 约束条件
1)轨道动力学约束
考虑质点模型,受地球引力约束,航天器与目标的轨道动力学约束为:
(11)
式中:r表示空间位置矢量,r对应其模,轨道动力学约束主要用于求解在非机动情况下航天器与目标的任意时刻空间位置。若考虑摄动影响,对于非近地轨道的卫星,其在轨运动过程中主要受地球非球形摄动的影响,在文献[22]中给出了考虑J2摄动影响时,简化的引力势函数:
(12)
式中:Re表示地球半径;φ表示航天器在球坐标系上的纬度。本文中采用文献[23]中的方法对Lambert结果进行修正:将Lambert求解速度增量附加给原轨道速度,从初始位置开始进行轨道递推,递推加速度由引力势函数的梯度获得。递推航天器运行时间长度后,根据实际求得的轨道位置与设定的目标轨道位置进行偏差计算,并用于更新下次迭代计算初始速度。最终在多次迭代后递推位置结果与设定位置结果趋于一致,获得了真实的变轨参数。
本文任务规划中考虑两种轨道动力学约束分析方式:先考虑式(11)中二体动力学约束对式(10) 中变量进行求解,再考虑式(12)中摄动约束对va和vb进行修正;第二种为直接考虑式(12)中摄动约束对式(10)中变量进行求解。
2) 服务时长约束
由于服务时长差异对于本文中算法求解效果影响不大,故此处考虑每个目标的服务时长为一固定值简化问题。
Ts=const
(13)
3) 目标服务次数约束
考虑每个目标被服务次数ns满足:
ns=1
(14)
4) 单航天器总时长约束
任一服务航天器任务总时长Ti约束:
max(Ti)≤T0,i=1,2,…,n
(15)
5) 单航天器燃料约束
以速度增量近似表示:
Δvi≤ΔVi,i=1,2,…,n
(16)
式中:Δvi表示任一服务航天器i任务中总速度增量消耗;ΔVi表示服务航天器i任务开始前携带燃料对应的可产生速度增量。
1.4 目标函数
在轨服务任务中,燃料消耗是重要的指标,通常要求在规定时间约束范围内尽可能地节省燃料。本文考虑时间紧迫性已由时间约束量表现,因此在规划中要求在给定的任务时长下尽可能地节省燃料消耗。针对于整体的数学求解模型,为了使的燃料总消耗代价最小,目标函数考虑采用如下形式:
(17)
2 改进启发式拍卖算法
传统的优化算法往往会从全局角度出发将目标适应度表述为优化变量的函数形式,并进行迭代求解获得最优的决策变量。拍卖算法则通过模拟拍卖活动,每个竞拍者根据“自利”原则依次对各个商品进行报价。多轮次的拍卖活动后,最终每个拍卖商品都尽可能在满足买家预期利润最大的前提下,找到对应的买家。在本论文中将服务航天器视为买家,目标任务视为拍卖品。
2.1 启发式目标优先级排列
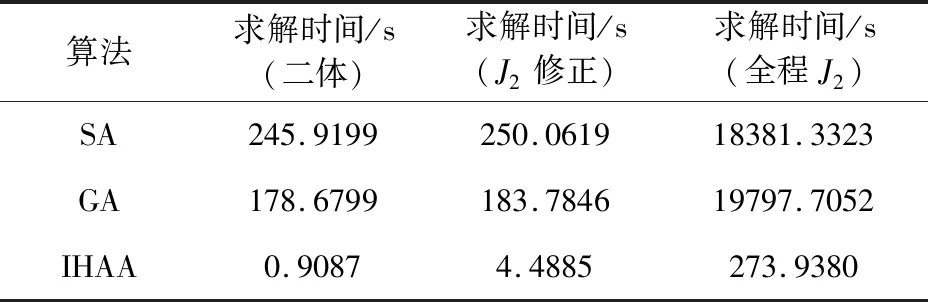
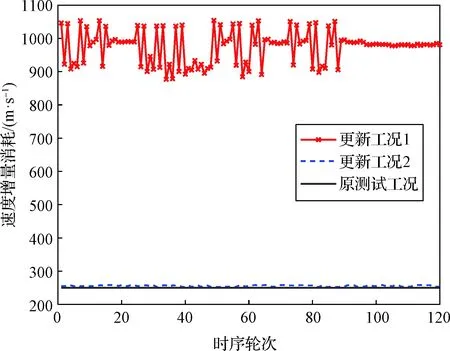
在本文中,考虑航天器数量n可能比目标数量m少,也可能比目标数量多。当n≥m时,将所有任务均进行分配即可,只有当重拍情况出现时会进行多轮拍卖;当n 在多轮拍卖的过程中需要确定每轮拍卖的目标集合,结果方案中每个服务航天器的服务序列取为拍得任务的顺序。在以往的拍卖算法实现案例中,由于对拍卖品的收入、价格计算一般都只需要考虑各拍卖品和各买家关系,通常进行随机分配。然而在轨服务领域的任务规划有一个显著特征:相同航天器分配得到的多个目标前后价格关联。服务航天器分配了一个任务后再去服务下一个目标,和直接服务下一个目标相比变轨代价不同。任意航天器对任意目标的服务代价不固定导致需要全局考虑,也是以往用优化算法进行求解运算量大的原因之一。 在本论文中,为了加快运算,引入启发式规则,在目标的服务时序确定上引入了先验知识,综合考虑变轨服务代价和目标重要度评分: Gj=Vj-Cj,j=1,2,…,m (18) 式中:Gj可以视为对于目标j的优先级评分;Vj表示对于目标j的重要度评分;Cj表示对于目标j的变轨代价评分。重要度评分需要综合变轨相关的信息给出,这里将变轨相关先验知识融入Cj进行表述,可以概括为如图3所示三项原则: a) 服务先近后远原则 对每一个服务航天器,先服务近的再服务远的变轨燃料消耗更小,如图3(a)中先服务1再服务2。 b) 就近服务原则 对每一个目标,尽可能要求接近的服务航天器去进行服务,如图3(b)中目标1优先B提供服务: c) 有限燃料聚集任务优先原则 当服务航天器数量或燃料资源有限时,注定部分目标无法被服务,这时优先考虑服务更聚集的目标,以在有限资源下尽量满足更多的服务需求。如图3(c)中A号服务航天器优先考虑服务1而不是4: 图3 先验知识Fig.3 Prior knowledge 然而当燃料充足时,过早地服务聚集目标将导致本可以服务的离群目标很难被覆盖,因此需要对航天器服务能力进行粗略的衡量。考虑两种工况: 1) 航天器与目标半长轴为42064169 m和42264169 m,偏心率均为零,轨道面夹角为1°; 2)航天器与目标半长轴均为42164169 m,偏心率均为零,其余参数相同; (19) 式中:ΔV0为速度增量修正量(共面共高下为零),可近似取为变轨时长t下的计算结果统计平均值。 图4 速度增量消耗与相位角差关系图Fig.4 Relation between Δv and phase difference 进一步可估算当前任务场景下服务能力系数η: (20) 式中:min(Δφj)表示目标j相对航天器集的最小相位角差,考虑到当η<1时,航天器集的整体服务能力较强,因此可以优先选取较近的目标服务;当η≥1,航天器集的整体服务能力较弱,可以优先选取更聚集的目标。为了尽可能得覆盖多数目标,考虑η≥1时快速趋向于第二种优先选取方式。设计系数α: (21) 融合上述先验知识,进行近似的变轨代价表述: (22) 对于每一个本轮次的拍卖任务j,需要计算每一个服务航天器i服务其的变轨代价(拍卖价格),即速度增量消耗,同时也用于后续的服务能力判断。当服务航天器无分配任务时,考虑在总时长约束范围内进行变轨速度增量求解,由式(5)给出,变轨代价和速度增量消耗Pij为: Pij=Δvij (23) (24) 对于每一个买家(服务航天器)i0,在轮次k的拍卖活动中,需要追求其自身的最大利润,选中的目标任务j0应满足: (25) i=1,2,…,n (26) (27) 式中:ε为设置正值参数,目的是使任务在被选中时必定提高价格,确保在多个买家相互竞争中任务成本不断上升,避免算法陷入死循环。ε值如果选大了会使得最终方案总利润降低,结果不理想;选小了则算法计算效率下降。后续若仍有买家i′依据式(25)原则选取目标任务j0,则认为发生了竞标冲突。 竞标冲突发生后,任务j0重新被分配给买家i′,同时任务j0的价格重新由式(26)和式(27)进行更新;买家i0重新在拍卖任务中选择利润最高的任务,并再次进行燃料约束判断及价格更新。若竞拍冲突再次发生,迭代重复上述过程,直到无竞拍冲突事件发生或航天器无法在满足燃料约束前提下分得任务。 以往的拍卖算法设计过程中,如果对于某一买家,本轮任务中没有一个任务满足约束条件,则认为该买家没有拍得任务。在航天器任务规划计算过程中,Lambert变轨过程的变轨时长是通过提前设置确定的,因此时间消耗必定不会超过阈值,考虑通过任务价格是否超过剩余速度增量来进行判断。 在拍卖结束后剩余未分配的任务认为流拍,但考虑到航天器任务分配中可能出现目标扎堆而服务航天器分散的可能:多个目标可以被同一个航天器进行服务,而不能被其他航天器服务。因此设计流拍的任务自动进入下一轮拍卖任务候选集进行重拍。 当所有买家均已竞价完毕,则认为本轮拍卖结束,拍卖成功的任务归属相应的买家并进入下一轮拍卖。在每一轮次的拍卖过程结束后,需要根据式(18)对所有剩余任务进行优先级更新,并选出下一轮拍卖任务,同时根据式(5),(24),(26)和(27)确定拍卖任务的速度消耗、价格。该过程为增量式分配,对于执行任务过程中新添加的任务或者未完成任务状态发生改变,可以更新剩余任务集实现快速规划。 拍卖算法整体的流程如框图5所示。当所有的任务均已分配完毕,或者在本轮次拍卖中所有拍卖品均流拍,则认为拍卖结束。若式(5)计算过程中未考虑摄动力影响,则对方案中速度脉冲进行修正,最终输出规划方案。 图5 改进启发式拍卖算法流程框图Fig.5 Schematic diagram of the improved heuristic auction algorithm 若将本文算法应用于航天器星上在线规划,需要设计计算体系。当任何一个航天器探测到需要清除的碎片目标,或者需要被保障时,将被服务目标的轨道六根数信息、时刻信息发布给其余服务航天器,所有服务航天器随机依次进行竞拍。算法实现过程中价格计算考虑二体动力学约束。 考虑实际在轨应用中服务航天器的运算能力存在差异,设计如图6集中式与分布式两种计算体系: 图6 计算体系Fig.6 Computing architecture (1)集中式体系主要考虑到服务航天器运算能力较低,要求计算中心航天器具备较强的运算能力,并对其依赖度高。计算中心航天器收集各服务航天器信息及发布的任务信息,进行集中式运算,各服务航天器按照随机顺序依次竞拍,最后将考虑摄动力约束修正后的规划指令下发各服务航天器执行。计算中心航天器也可以具备任务信息发布的能力。 (2)分布式体系要求服务航天器具备一定的运算能力进行分布式信息交互与运算。该模式下任意服务航天器出现故障对其他服务航天器影响较小。可以用图G(V,E)表示服务航天器通信网络的拓扑结构,图中点的集合V表示服务航天器集合U,E表示连接各节点的边。如果两个服务航天器可以通信,则存在连接这两个节点的边;若任意两个节点间至少存在一条链路,则称通信网络是联通的。本文中假设满足联通要求,由于分布式体系中没有计算中心收集并发布每轮次任务信息、价格信息,因此需通过信息交互过程计算得出。具体步骤为: a)各任务发布航天器发布任务,所有服务航天器通过信息交互获得任务集; b)通过信息交互各服务航天器获得该轮次任务优先级排序结果,判定该轮次分配任务集; c)通过信息交互各服务航天器获得所有任务价格信息、收入信息,按照随机顺序进行竞拍。竞拍过程中也依赖于信息交互进行价格更新、冲突解决; d)该轮次任务分配后进入下一轮次,直到满足结束条件。各服务航天器分别考虑摄动力约束对自身分得任务进行速度脉冲修正、执行。 本节将设置算例对本文所提出的算法进行仿真验证。仿真过程采用个人计算机完成,CPU型号为Intel Core i5-10210U@1.6G Hz,内存为16 GB。设计在某次在轨服务任务中,有5个服务航天器和20个待服务目标,每个服务航天器携带燃料可以满足200 m/s的速度增量产生,要求在10天内完成多对多在轨服务任务,目标的重要度评分相同,各服务航天器对所有目标的收入相同。设置双方轨道偏心率和近地点幅角均为零,其余六根数信息服务航天器见表2,目标任务见表3。服务航天器和目标的轨道倾角、升交点赤经在正负0.05°之间随机选取,平近点角在50°至60°之间随机选取。 表2 各服务航天器轨道参数Table 2 Orbital parameters of each servicing spacecraft 表3 目标轨道参数Table 3 Orbital parameters of each target 续表3 将本文设计算法与常用的遗传算法(GA)与模拟退火算法(SA)进行比较。其中模拟退火算法与遗传算法为了保证对比的有效性和快速性,针对一对多部分时序取优过程统一采用模拟退火算法实现,多对多规划部分迭代初值采用随机选取。考虑加速运算,均加入了一对多规划结果历史存储与查询部分,以减少重复运算,仿真时间均设定为2022年5月10日04∶00∶00~2022年5月20日04∶00∶00。算法参数设定变轨时间修正量1800 s,代价更新ε取为0.05,GA种群规模和SA马尔科夫链长度取为10,GA最大遗传代数取为50,SA初始温度数值取为100,SA衰减参数取为0.8,服务时长取为1800 s。 改进启发式拍卖算法(Improved heuristic auction algorithm,IHAA)任务规划结果见表4和表5,考虑二体动力学约束、J2摄动计算价格规划结果相同,速度增量消耗总量均为250.0093 m/s。 表4 任务规划结果(部分)Table 4 Part of the task planning results 表5 任务分配结果Table 5 Task assignment results 为了验证本文算法的快速性和有效性,以IHAA算法结果目标函数值作为遗传算法与模拟退火算法的迭代结束条件,以对比达到同样性能时,三种算法的求解效率差异,仿真对比结果见表6。 表6 三种算法求解效率对比Table 6 Comparison of the efficiency of three algorithms 表6中第二列表示仅考虑二体动力学计算算法中每一步目标函数(拍卖价格);第三列表示对第二列结果(两次脉冲速度矢量)考虑J2摄动影响进行修正后的总耗时;第四列表示每一步目标函数(拍卖价格)计算时便考虑J2摄动影响。三类算法速度增量消耗与迭代次数变化关系对比如图7所示。 图7 三种算法迭代计算对比图Fig.7 Comparison of iterative calculation of three algorithms IHAA算法不存在迭代次数的概念,考虑对比效果在图7中画为一条直线。观察结果可以看出拍卖算法在短时间内能快速给出一个相对较优的方案,在时间上相对于传统优化算法有极大优势,能大幅度提高求解效率,尤其是仅考虑二体动力学约束计算拍卖价格时,具备星上自主在线规划潜力(考虑J2摄动修正机动指令可由各执行航天器分别计算)。 当考虑燃料不充足时,设置所有服务航天器携带燃料可以满足10 m/s的速度增量产生,仍然要求十天内完成任务,此时GA算法和SA算法均无法得到有效解,IHAA算法实现分配结果如表7所示。可以看出当燃料资源紧张时,相比于优化算法无法给出规划,IHAA仍然可以实现部分结果输出。 表7 燃料不充足时任务分配结果Table 7 Task assignment results when fuel is insufficient 无论是集中式计算体系还是分布式计算体系,都需要确定各服务航天器的竞拍顺序。设计中各服务航天器可按照随机顺序依次竞拍,需要分析该策略对于分配方案结果的影响。实验中改变5个服务航天器的竞拍顺序,每次规划方案在形成规划方案后对两次脉冲速度矢量考虑J2摄动影响修正,共120种时序下计算速度增量总消耗值的变化情况。 图8 速度增量消耗与竞拍时序关系图Fig.8 Relation between Δv and auction order 图8中更新工况1航天器速度增量改为1000 m/s,双方平近点角在50°至100°间随机选取更新,更新工况2将ε值调整为0.5。可以看出,不同的航天器竞拍顺序对于最终规划方案影响相对较小,且速度增量消耗量优于优化算法初始多轮次的计算结果,具体与双方轨道根数、代价更新ε值等有关。在本文算例中,120种竞拍顺序最终燃料消耗相同,规划结果也相同。可以看出随机顺序策略具备可行性。 本文针对GEO航天器多对多在轨服务任务规划问题建立了数学模型,探索运用拍卖算法实现快速的规划方案制定,设计了改进启发式拍卖算法,解决了传统优化算法制定规划方案耗时久、计算资源消耗大的问题,最后通过仿真实验验证了所提算法的有效性和可行性。研究成果及总结如下: 1) 建立了基于Lambert变轨的规划问题数学表征,并在给定变轨时长约束前提下快速确定变轨时长与速度增量消耗,可用于拍卖算法的价格计算和优化算法的代价函数计算。 2) 提出了基于拍卖算法的快速规划,针对拍卖品的时序确定问题提出了一种基于先验知识的确定策略,并设计了重拍机制以增加目标的被选中概率,在考虑J2摄动影响下给出最终任务规划方案。仿真测试结果表明,与遗传算法、模拟退火优化算法相比,具有更高效的“次优”方案确定能力,在动态环境下(突发事件发生或新任务添加)相比传统优化算法更快速,具备快速形成有效规划方案的能力。 3) 在燃料、时间约束限制强时,优化算法往往难以找到可行的迭代初值导致无解,而此时本文所提算法可以给出部分可行方案。但同时也可能会出现实际可以覆盖所有任务,但方案未实现全分配的现象,这是由算法结果并不是全局最优解导致的。 4) 鉴于本文算法的快速性,后续可考虑用于效能评估指导服务航天器空间部署。同时本文设计了集中式与分布式两种计算体系,后续可考虑应用于星上规划平台。若运算时间充裕,允许多次迭代优化,本文算法亦适用于优化算法的初值寻找。
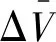


2.2 拍卖任务价格计算

2.3 出价策略设计
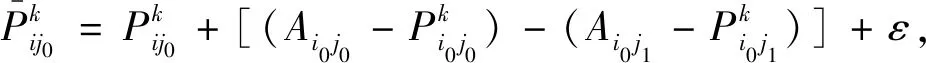

2.4 竞标冲突过程设计
2.5 重拍机制设计
2.6 中标机制
2.7 方案确定

2.8 星上在线规划

3 仿真校验
3.1 仿真工况

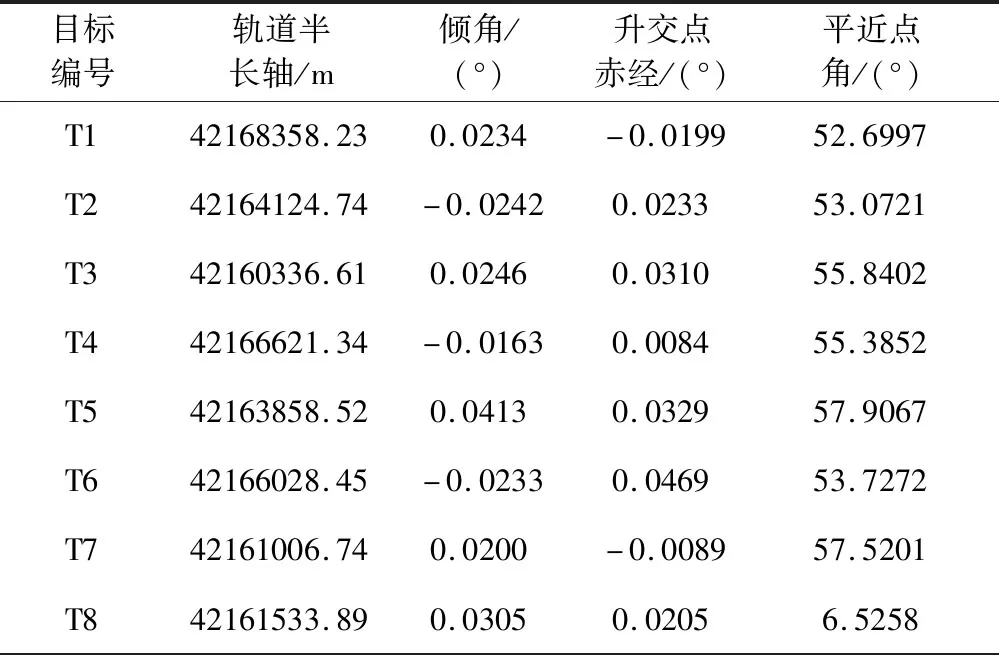
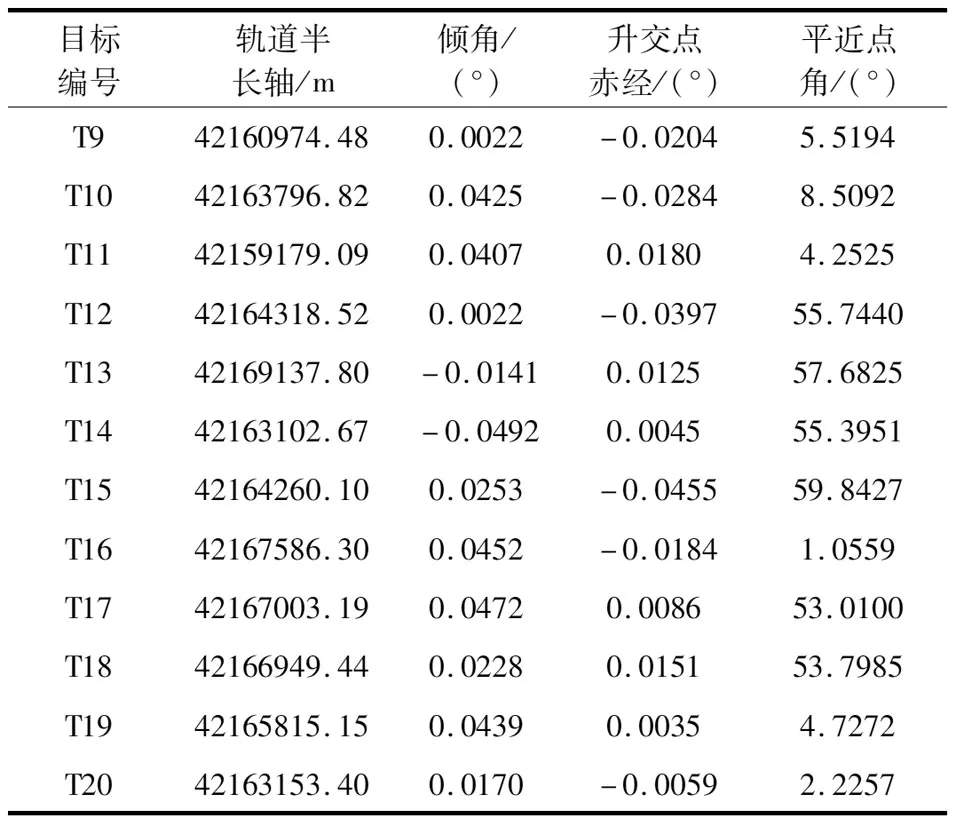
3.2 算法效率对比
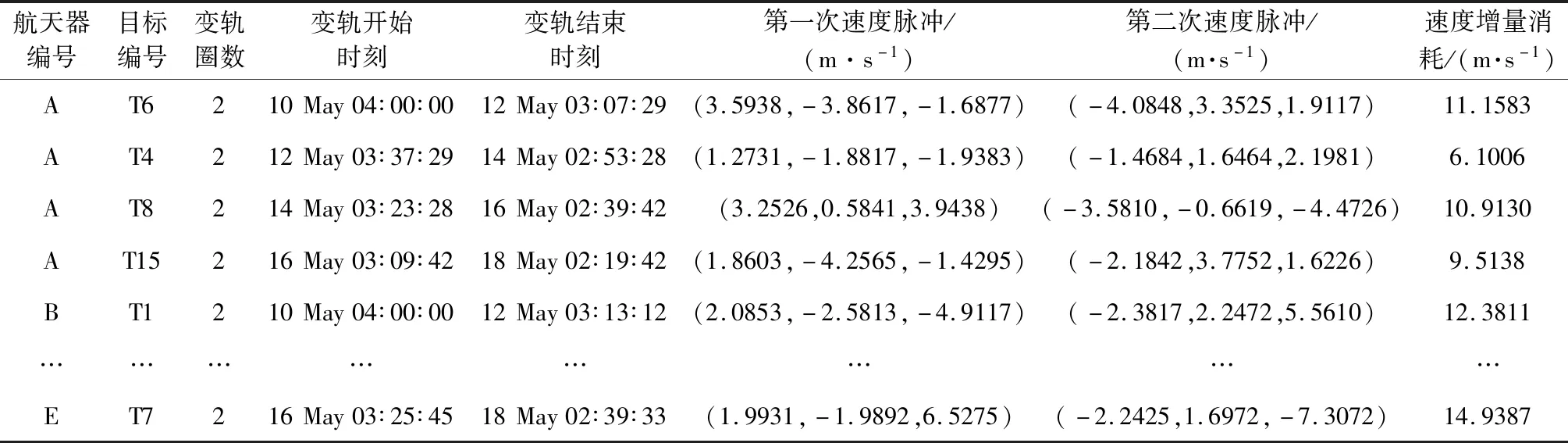



3.3 买家竞拍顺序影响分析
4 结 论

