具有自然年龄和染病年龄的SIQS传染病模型的稳定性

王时雯，由守科

(新疆大学 数学与系统科学学院， 乌鲁木齐 830017)

0 引言

隔离是切断传染病传播途径的最直接和有效的措施，对防控SARS、COVID-19等恶性传染病有重要作用[1-3]。近年来，人们建立了许多带有隔离的微分方程SIQS传染病模型，并对这些模型的阈值理论或解的持久性进行了研究[4-9]。 然而，这些模型大多没有考虑自然年龄和染病年龄因素对传染病传播的影响，并不能准确反映乙肝、艾滋病等具有较长染病周期的传染病的传播。因此，传染病模型研究中综合考虑自然年龄、染病年龄和隔离措施是必要的。

1974年，Hoppensteadt[10]综合考虑隔离、人口迁移、类年龄因素对传染病传播的影响，建立了一类自然年龄和染病年龄并存的SIQR传染病模型，但由于模型结构复杂，该模型解的阈值问题至今未得到解决。之后，相对简单的自然年龄和染病年龄结构的SIR、SIQR、SEIS、SEIR等传染病模型解的适定性得到证明[11-14]，但关于平衡解的阈值理论的研究结果较少。至今，自然年龄和染病年龄结构并存的传染病模型的阈值理论尚无一般结论，只有一些针对具体模型阈值理论的研究结果[15-16]。

1 模型

根据Kermack和Mckendric的传染病仓室模型思想[17-18]，文献[19]中建立的一类自然年龄和染病年龄结构并存的SIS模型增加隔离类人群，将人群分为易感类、染病类和隔离类，并假设传染病无垂直传染性，建立如下SIQS传染病模型：

(1)

定解条件为

(2)

模型中未知函数S(t,x)、I(t,x,y)、Q(t,x)依次表示易感类、染病类及隔离类人群关于时间t、自然年龄x和染病年龄y的分布密度函数。A为最大年龄，0≤x,y≤A，且y>x时I(t,x,y)=0。参数u(x)、b(x)、λ(x)、g(x,y)依次表示死亡率、出生率、发病率、隔离率函数。r1(x)、r2(x)分别表示隔离类和染病类人群的治愈率函数。S0(x)、I0(x,y)、Q0(x)分别表示3类人群的初始分布密度函数。另外，假设模型中相关函数满足：

(H1)：S0(x),I0(x,y),Q0(x)在x,y∈[0,A)上是非负连续的有界函数，且S0(x),Q0(x)∈L1((0,A);R)，I0(x,y)∈L1((0,A)×(0,A);R)。

(H2)：r1(x),r2(x),b(x),λ(x),g(x,y)在x,y∈[0,A)上是非负连续的有界函数，u(x)连续且

模型(1)和(2)是非线性双曲方程组，利用压缩映射原理和先验估计的标准性方法[20]可以证明非负解的存在性。本文将证明该模型无病平衡解的稳定性和地方病平衡解的存在性。

2 等价模型

联合模型(1)-(2)得到总人口分布密度函数为

满足定解问题

(3)

根据文献[21]，如果假设

成立，则定解问题(3)存在平衡解

其中

令

S(t,x)=s(t,x)P∞(x),I(t,x,y)=i(t,x,y)P∞(x),Q(t,x)=q(t,x)P∞(x)

代入模型(1)和(2)可得方程

(4)

及定解条件

(5)

其中

从而，对模型(1)和(2)平衡解的研究可归结为对模型(4)和(5)平衡解的研究。

3 无病平衡解稳定性分析

假设(s*(x),i*(x,y),q*(x))为模型(4)和(5)的平衡解，则

(6)

显然

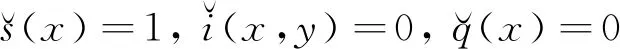
(7)

其中

简单计算可得

令R=F(0)，即

证明令J(μ)=F(μ)-1，则J(μ)为μ的单调递减连续函数。当R>1时，J(0)=R-1>0，且

F(μ*)=1=|F(a+ib)|≤F(a)

证明利用特征线方法解得模型(4)和(5)的解为

(8)

(9)

(10)

令h(t,x)=λ(x)I1(t)s(t,x)，由于0≤s(t,x)≤1，故当t>A时

即

(11)

(12)

其中

从而

又因为R<1，则M=0。于是，根据式(12)可得

(13)

联合式(8)—(10)和式(13)得

4 地方病平衡解的存在性

当R>1时，受文献[21-22]的启发，利用Volterra积分方程理论，可得地方病平衡解存在性定理。

定理3当R>1时，模型(4)和(5)至少存在1个地方病平衡解。

(14)

由式(14)计算得

(15)

(16)

(17)

其中

综上，当R>1时模型(4)和(5)存在地方病平衡解。证毕。

5 结论

讨论了一类带有隔离和染病年龄的SIQS偏微分传染病模型的阈值理论，得到了阈值R，给出了无病平衡解稳定性和地方病平衡解存在性的条件。从模型的阈值R的表示看，对染病类人群的隔离和治愈是控制疾病传播的关键因素，这在防控SARS和COVID-19疫情中已得到体现。地方病平衡解的唯一性与稳定性问题是后续研究的内容。