汇集知识,融会贯通,收获方法
——一道几何题的教学与思考
陈秀清
天津市静海区大邱庄镇中学 301606
学生学习兴趣的培养比学习方法重要,学习方法比学习知识重要.在解题教学中,教师要引导学生积极参与,同一道题不要局限于一种解法,要通过多法探究,培养学生的发散思维,进而实现知识的融合贯通.笔者通过一题多解的教学,融合初中几何众多重要知识,以使学生收获多种求解线段的方法与思路.
真题再现
问题:如图1所示,已知四边形ABCD是边长为1的正方形,点E是线段AD的中点,连接BE得到△ABE,将△ABE沿直线BE折叠得到△FBE,BF与AC相交于点G,求线段CG的长.
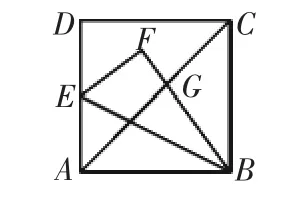
图1
这是一道以正方形为背景的几何综合题,综合考查了轴对称的性质、正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质、平行线分线段成比例定理、勾股定理以及三角函数等重要知识.学生需要根据题意作出辅助线,构造全等三角形与相似三角形,然后利用它们的性质解答,其中渗透了数形结合、转化等数学思想,是一道较好的几何综合题.
解法探究
师:通过阅读试题,可得到的已知条件包括:正方形ABCD的边长为1,点E是AD的中点,△FBE 是△ABE 沿直线BE折叠得到,AC是正方形ABCD的对角线,所求问题是求线段CG的长.当然线段CG的长不能直接去求,必须找到与线段CG相关的结构,从CG相关的结构入手找到已知与未知的连接点,与线段CG相关的结构有哪些呢?
生1:从图1可以看出,与线段CG相关的结构包括:线段AC,△CGB,△AGB.

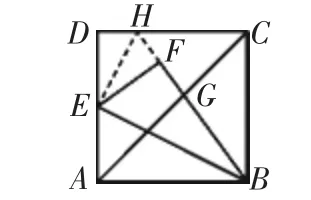
图2

师:上述两位同学都致力于求线段DH或HF的长,分别采用了相似三角形与射影定理,其他的步骤都相同,那么求线段DH或HF的长,还有没有其他的方法呢?


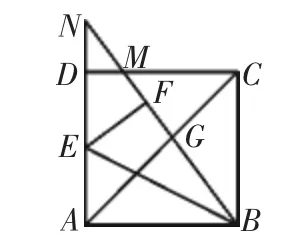
图3

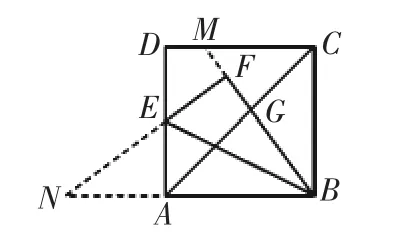
图4


图5
师:这位同学把问题集在锐角三角形GAB中,通过解直角三角形求得AG的长,从而求得CG的长.在上述的不同解法中,分别展现了求线段长的三种方法,一是利用直角三角形的勾股定理求线段段长;二是利用相似三角形对应边成比例求线段长;三是利用解直角三角形求线段长,这些都是我们宝贵的解题经验.
教后反思
(一)重视学生体验知识的生成过程
学生学习知识是一个探索、发现、感悟的过程[1],在此过程中,学生 不仅收获了知识,而且体验到了知识的生成过程,收获了解题方法与数学思想.在本课教学中,学生通过求与CG相关的量从而求得CG的值,体会到了转化的数学思想.学生还通过添加辅助线构造直角三角形、相似三角形、全等三角形,利用直角三角形的性质、相似三角形的性质、全等三角形的性质解决问题,体会到了构造法在解题过程中的重要性.同时,在探索的过程中,学生相互启发,由此及彼,由点及面,不断生发思维的火花,促进了思维的发展.由此可见,数学教学应重视探究知识的生成过程,让学生在独立思考、小组交流中经历知识生成的过程,体验数学思想方法,从而获得探索的快乐.
(二)在规律探究中培养学生思考力
鲜活的问题是规律探究的有效载体.实际上,学习数学就是通过解决问题发现其中的内在规律,然后运用规律解决问题.规律的内涵丰富多样,可以是通项公式,可以是计算方法技巧,也可以是解决某类问题的思路与步骤,还可以是抽象出来的数学思想方法.解决完具体问题后,不能局限于这一个问题,应通过追问与探索,看看解决问题的方法是否具有普遍性与规律性,问题的结论是否可以进一步延伸?数学问题千变万化,但数学规律是恒定不变的.如在本例中,学生发现在某一个三角形中,已知一个角的度数与另一个角的正切值,还有一条边长,就可以解这个三角形,求出任意一边的长,方法是过第三个角的顶点作垂线,构造两个直角三角形,利用勾股定理建立方程可以求得相应线段的长.又如,在复杂的图形中,发现其中的基本图形,如本例中有一线三等角模型、三垂直模型,还有A型相似、X型相似、反A型相似、反X型相似等.因此,在数学教学中,教师要有意识地培养学生探究规律的意识,不断提高学生的数学学科素养[2].
(三)在融会贯通中加强知识的运用
数学知识是具有逻辑关系的一个知识体系[3].数学教师要帮助学生不断加固知识结构,提高学生综合运用知识的能力,让学生既见树木又见森林.在本题的探究过程中,并没有单纯以解答问题为目的,而是注重了解法的对比联系,通过一题多解的形式促进学生多维思考,又通过多解归一实现知识的融会贯通.学生探究出了五种解法,拓宽了思维路径,培养了发散思维.同时,通过基本图形的发掘与基本方法的发现,学生能实现知识的内在统一.

