基于心理物理学实验的非荧光织物白度公式评价

杨红英， 齐梦园， 杨志晖， 杨艳丽， 张靖晶， 谢宛姿

(1.中原工学院 纺织学院， 河南 郑州 450007； 2.青岛大学 纺织服装学院， 山东 青岛 266100； 3.江南大学 纺织科学与工程学院， 江苏 无锡 214122)

白色在色彩中占据重要地位，对于工业原料及产品尤其重要。GB/T 17749—2008 《白度的表示方法》 规定白度是表征物体色白的程度，白度评价结果直接关乎产品质量、等级划分及质量控制。以主观方式评价样品白度时，容易受到观察者自身的主观因素和环境等客观因素的影响，其结果也不易精准表达和客观定量。客观评价样品白度，不仅能进行准确表达和传递，并能给出准确结果。1986年，国际照明委员会(CIE)在Ganz等[1-3]研究的基础上推荐了白度公式，命名为CIE公式。通过计算白度指数和色泽指数，评价白度与色调取向。此公式方便简洁，然而在与视觉评估之间的一致性方面还有待提升，且白度范围存有诟病[4-6]。

对白度公式的评价，从与视觉评估之间的一致性展开。白度公式在纺织品、纸张、塑料以及牙科等方面都有应用，有研究者借助这些材料对白度公式的预测性能进行研究，致力于为不同行业选用合适的白度公式提供依据[7-9]。Katayama等[10]基于非荧光与荧光涤纶织物，采用排序法，以Spearman相关系数和Pearson相关系数比较了17种白度指数，其结果认为C/V白度公式(WC/V)、Grum白度公式(WGrum)、CIE白度公式(WCIE)和Uchida白度公式(WUchida)预测性能最好。He等[6]基于非荧光和荧光纺织品进行目视评价，表明LAB白度公式(WLAB)预测性能较好，且在均匀性、适用性和视觉相关性方面均优于CIE白度公式及其他公式。Jafari等[11]基于非荧光和荧光棉织物，使用成对比较法对CIE和Uchida白度公式进行比较发现，CIE白度公式优于Uchida白度公式。Chen[12]基于非荧光和荧光棉织物，使用量值估计法进行目视评价，结果表明CIE白度公式较好于C/V和Uchida白度公式。可见，采用不同方法进行实验研究，其结论不尽相同，且以上研究未给出适合非荧光增白纺织品应用的公式。

本文作者课题组前期基于荧光织物评价白色公式，发现无论对于CIE白度范围内还是范围外的织物，在Ganz白度公式(WGanz)、CIE白度公式、Uchida白度公式、WUV白度公式(WUV)、WLAB白度公式(WLAB)、Hunter2白度公式(WHunter2)和WC/V这7个白度公式中，Hunter2公式的评价效果最接近人眼视觉评价结果[13]。

本文基于前期研究，进一步采用白色辨识实验挑选白色样品，选用心理物理学视觉实验中的成对比较法和类别判定法，综合分析和评价9个白度公式，即Hunter1白度公式(WHunter1)、WHunter2、WGanz、WGrum、WCIE10、WUchida、WC/V、WUV、WLAB的白度预测性能。

1 实验部分

1.1 实验材料与仪器

实验材料：涤纶平纹织物(面密度为135 g/m2)，中恒大耀纺织科技有限公司；匀染剂PLA-340，分散红(Red RD-E)、蓝(Blue RD-E)、黄(Yellow RD-E)染料，上虞精联贸易有限公司。

实验仪器：L2002A Smart Dyer万能染色联合试验机、高精度HunterLab UltraScan PRO分光测色计、X-Rite SpectraLight QC标准光源箱。

1.2 样品制备

制备带色样品时，将分散染料进行稀释，再按照一定比例添加到染色浴中，进行染色。染色采用高温高压工艺，织物质量为4 g，pH值为5，浴比为1:30，染色工艺曲线如图1所示。染色后进行水洗和烘干，制备样品120个。

图1 染色工艺曲线Fig.1 Dyeing process curve

1.3 样品测色

测色前，首先校正HunterLab UltraScan PRO分光测色计。测色时，将样品折叠至不透光，取样品4个不同位置的平均值。选用D65照明体，包含镜面反射；测量孔径为19 mm，测量范围为350～780 nm，间隔为5 nm。

1.4 心理物理学评价实验

共进行3组心理物理学视觉评价实验，首先是白色辨识实验，用于挑选白色样品；然后是成对比较实验，要求观察者判断一对样品的白度大小；最后是类别判定实验，要求观察者判定样品属于哪个白度等级。

视觉评价在暗室中，于SpectraLight QC标准观察箱的D65光源下进行。箱体为中性灰，观察条件为0/45，观察距离约为50 cm。成对比较实验中招募了包含10位女性和7位男性在内的17名观察者；类别判定实验中招募包含5位女性与4位男性在内的9名观察者。所有观察者年龄在23～28岁之间，三色视觉正常，矫正视力为5.0。

为确保样品大小一致且便于观察，将样布折叠在4 cm×7 cm的硬纸板上。实验开始前，观察者1 min暗适应在暗室中进行，1 min亮适应在灯箱下的D65光源中进行[14]。为保证实验结果的准确性，每位观察者单次观察时间不超过30 min。

1.4.1 白色辨识实验

为确保具备9个白度公式都适用的样品条件，实验样品均处于CIE白度公式规定的白度范围内。

向观察者展示120个自制样品，观察者做出判断：1)一次性出示所有样品，区分观察者认为的白色样品和彩色样品；2)依次随机出示1个样品，判断该样品是彩色还是白色。通过以上步骤，一共选出分布广泛且均匀的113个白色样品，其中28个样品用于成对比较实验，85个样品用于类别判定实验。通过白色辨识实验挑选113个白色样品在CIE1964x-y色度图中的分布如图2所示。

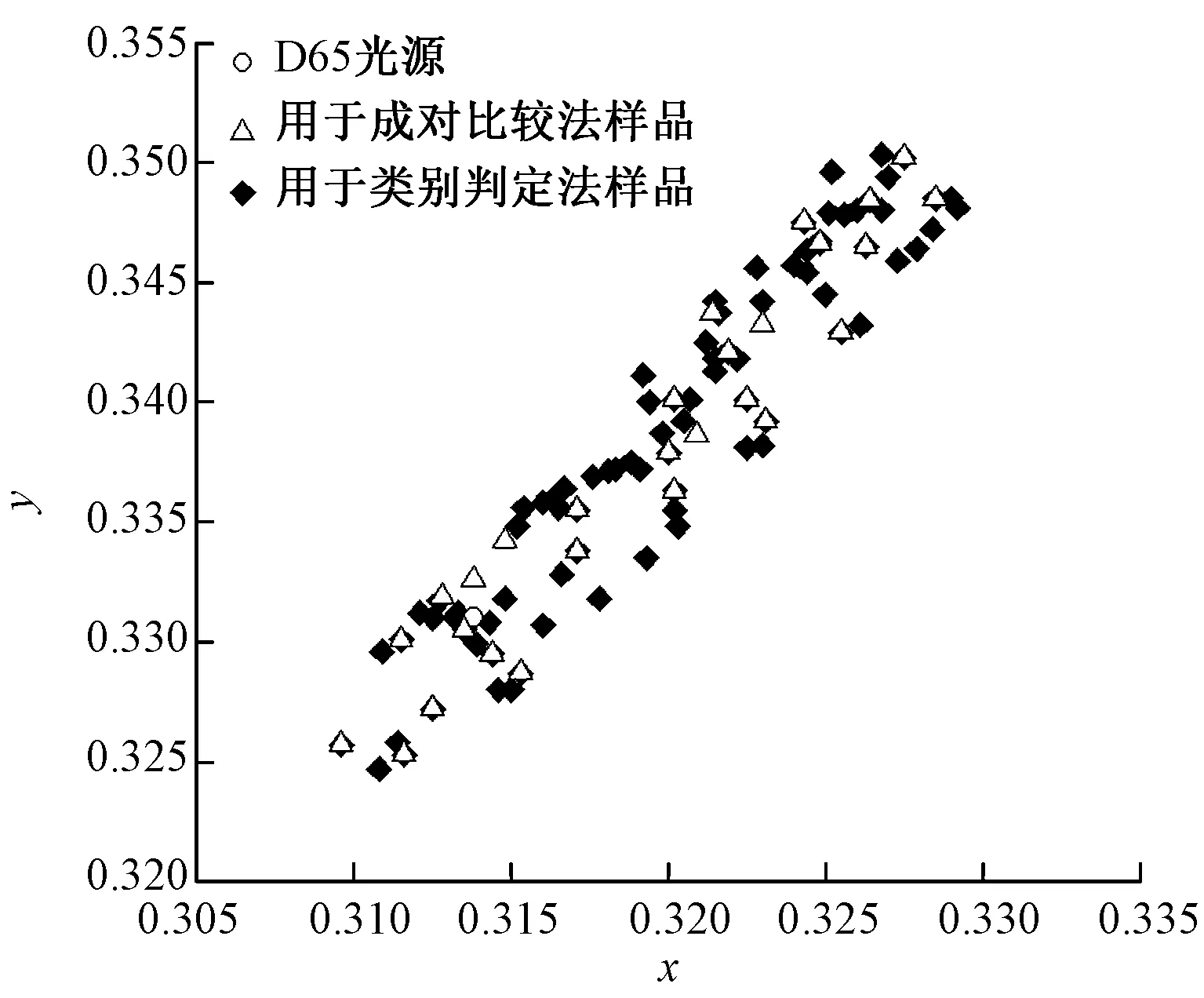
图2 心理物理学实验用白色样品在色度图中的分布Fig.2 Distribution of white samples for psychophysics experiments in chromaticity diagram

1.4.2 成对比较实验

将28块样品以随机样品对的形式展示给观察者，将其并列放置于标准观察箱中，观察者区分样品对的白度大小，共评价了378组样品对。为进一步评估观察者精度，17位观察者中有7位观察者进行重复性实验。每个样品进行24次评判，获得9 072个视觉评估数据(378组×24次)。

1.4.3 类别判定实验

类别判定实验时，观察者直接对样品白的程度进行判断，判断参考事先制定的标准进行。本文中的标准采用由Bartleson[15]提出的1～9级的心理物理学量表，定义如表1所示。

操作者从85块样品中任取1块样品，将样品置于标准观察箱中央，观察者在5 s之内做出类别得分判断。该实验相对较难，为保证准确性，9名观察者均对样品进行2次视觉评估。每个样品被评价18次，共计获得1 530个主观评价数据(85个×18次)。

2 数据处理

2.1 白度计算

分别利用WHunter1、WHunter2、WGanz、WGrum、WCIE10、WUchida、WC/V、WUV和WLAB共9个公式计算白色辨识实验获得113个白色样品的白度值。

2.2 观察者精度检验

2.2.1 成对比较实验观察者精度

采用误判率WD[17]表征成对比较法中的观察者精度，其包含重复性精度和准确性精度，其值越小准确性越高。对于观察者重复性的评价，是观察者2次判断的一致性，2次判断结果不一致则为误判。重复性精度是判断错误次数除以总数。对观察者准确性的评价，是观察者与所有观察者判断的一致性，若观察者给出与半数人不同的判断结果，则认为误判。用此位观察者误判次数比总数，以百分数表示误判率。观察者精度见表2，与经典数据相比精度较高，证明本实验数据有效[17-18]。

表2 成对比较法观察者精度Tab.2 Observer precision in pairwise comparison experiments

2.2.2 类别判定实验观察者精度

采用变异系数CV值评价类别判定法观察者精度，CV值越大，实验精度越差。CV值计算公式为

式中：n是样品总数。对观察者重复性进行评价时，xi和yi分别为观察者对同一样品第1次和第2次的评价数据；对观察者准确性进行评价时，xi和yi分别为此观察者和所有观察者对此样品评价数据的均值。

计算观察者精度，此实验中观察者准确性精度平均值为23.91%，从17.57%变化到28.35%；观察者重复性精度平均值为25.93%，从24.64%变化到27.34%。对比经典数据，均在可接受范围内，说明本文实验数据可靠[16]。

2.3 视觉白度差计算

2.3.1 成对比较法视觉白度差

采用Thurstone比较判断数据处理方法[19]，将目视评价获得的非等距量表转变成等距量表z-score，然后利用Coates等[20]的方法转换为视觉白度。统计观察者的目视评价数据，获得样品频数矩阵Fij，部分数据见表3。表中数据是经由视觉实验判断，所在列样品白度大于所在行样品白度的次数。计算频率矩阵Pij，将轴线空白处计为0.5。再将频率矩阵以标准正态分布的反函数转换成z-score矩阵，得出每一列的平均值，按照升序排列于表4，其数值越大，颜色越白。

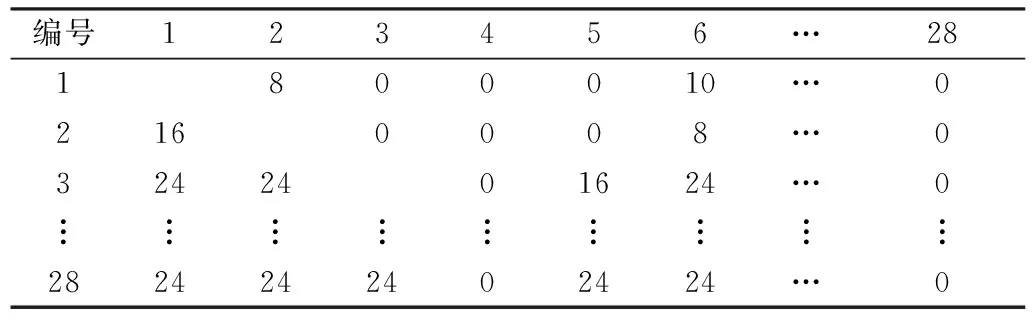
表3 成对比较法视觉实验的频数矩阵Tab.3 Frequency matrix from pairwise comparison visual experiments

表4 成对比较法视觉实验中所得z-score矩阵按升序排列Tab.4 z-score matrix in ascending order obtained from pairwise comparison visual experiment

将表4中2列相邻的数据右侧减左侧，求平均值，获得2块样品的视觉白度差Δvi。具有最小z-score值的是26号样品，将其转换为每块样品与26号样品的视觉白度差Δvi-Δv26，结果如表5所示。

表5 成对比较法中各样品与26号样品的视觉白度差Tab.5 Visual whiteness differences between each color sample and No.26 sample from pairwise comparison experiment

将表5中视觉白度差按照一定比例k缩放，即得最终视觉白度差ΔV，k的形式见下式：

式中：D(Δvi-Δv26)为原始视觉白度差的均值；D(ΔWi-ΔW26)为9个待评估白度公式的计算白度差的均值。

将视觉白度差进行缩放的目的是使最终的视觉白度差与计算白度差具有相同的当量，利于统计分析。28个样品的最终视觉白度差见图3。

图3 28个非荧光样品的视觉白度差ΔVFig.3 Visual whiteness difference ΔV of 28 non-fluorescent samples

2.3.2 类别判定法视觉白度差

根据Torgerson的类别判定法则[21]，将原始视觉数据转换成等分值数据。以18次视觉判断得到样品的评分值，计算频数矩阵，频数矩阵是样品被分配到各个类别的次数。样品被归类到小于等于该类别均可计入累计频数，将累计频数按照标准正态分布的反函数的形式转换成z-score矩阵。与成对比较法相同，将按照升序排列的z-score矩阵相邻右边列减去左边列，得到相邻边界的平均差异值。最后令初始边界为0，计算等距量表，获得在其感知属性量上的等距分值，最终计算结果如表6所示。

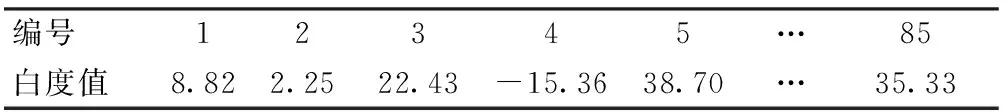
表6 类别判定法样品视觉白度差Tab.6 Visual whiteness difference of samples by category judgment method

3 结果与讨论

采用标准化残差平方和(Standardized Residual Sum of Squares，简称STRESS)[8]，误判率WD[17]，Spearman相关系数ρ[10]，Pearson相关系数γ[22]和F检验[23]，统计计算各白度公式的视觉白度差ΔV与计算白度差ΔW，评价其预测性能，结果见表7～9。对其预测性能的排序见括号内数字，数字越小，预测性能越好；最后一行是基于几种评价方式的综合评价，其数值越小，公式效果越好。

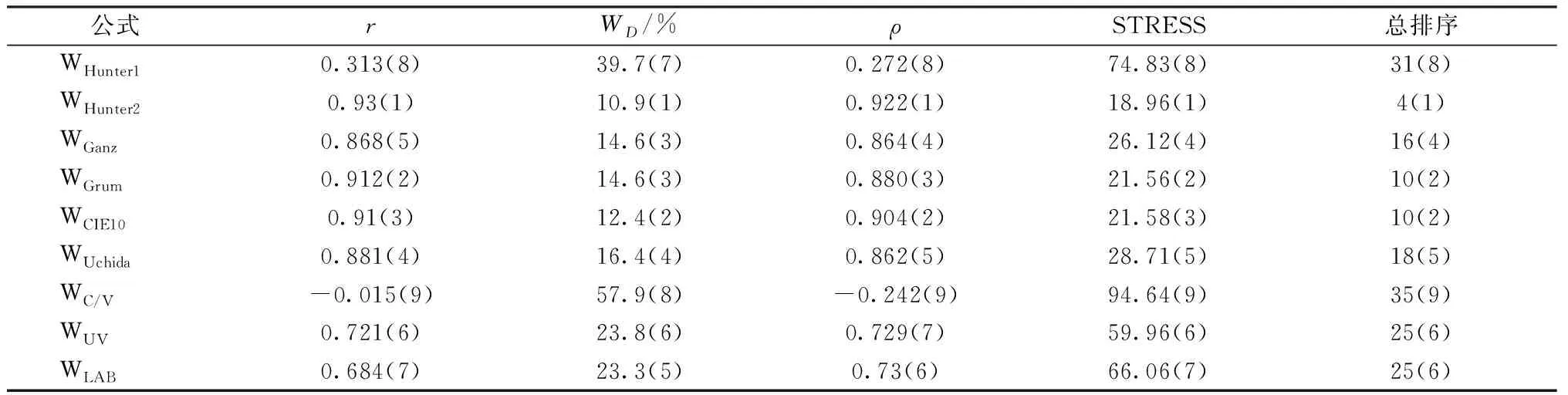
表7 成对比较法检验白度公式的预测性能Tab.7 Predictive performance of whiteness formulas from Paired comparison method

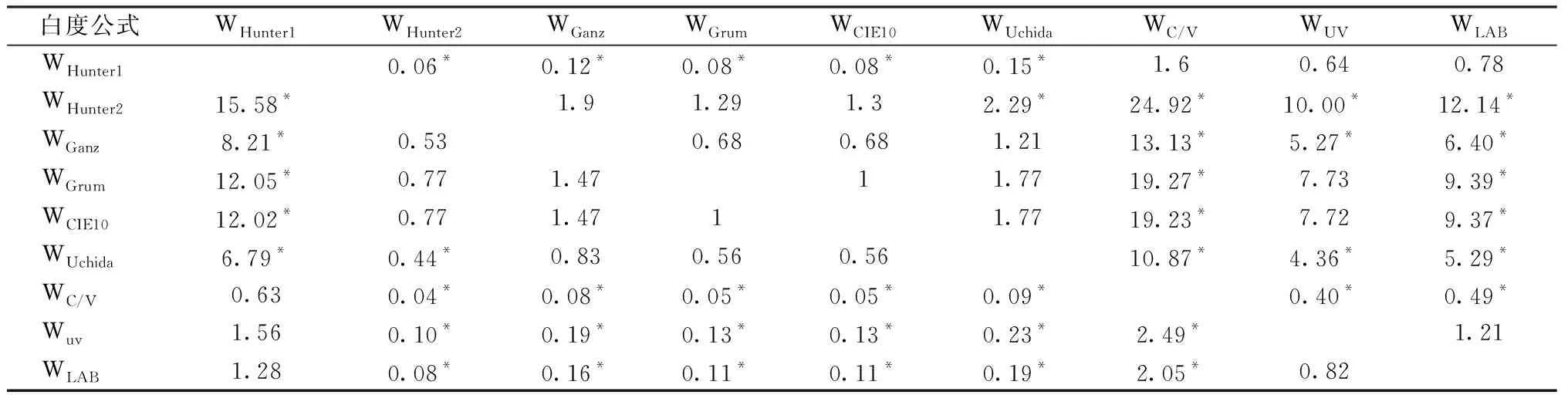
表8 成对比较法对比白度公式的预测性能(F检验)Tab.8 Comparison of Predictive performance of whiteness formulas from pairwise comparison method (F-test)

表9 类别判定法评价白度公式的预测性能Tab.9 Predictive performance of whiteness formula by category judgment method

3.1 基于成对比较法评价白度公式

对成对比较法实验数据采用STRESS、WD、Spearman-r、Pearson-ρ进行白度公式预测性能检验，以F检验考察公式预测性能差异的显著性，置信度取0.95(其中Fc为F分布中95%置信区间的临界界限)。当F>1/Fc时，所在行公式显著优于所在列；当1

对ΔV与ΔW进行线性拟合，r表示其相关系数，相关系数越大，二者间的相关性越好，反之则越差，结果见图4。可以发现：WHunter2、WGrum和WCIE10公式表现较好，数据点靠近趋势线且较为集中；WC/V和WHunter1表现很差，数据点十分分散，基本不相关和弱相关。

图4 成对比较法中28个样品的视觉白度差ΔV与计算白度差ΔW的比较Fig.4 Comparison of visual whiteness difference ΔV and calculated whiteness difference ΔW of 28 samples by pairwise comparison method

由表7结果可知：当以成对比较法评价白度公式时，WHunter2公式表现最好，且4个评价指标排名一致；然后是WGrum、WCIE10、WGanz、WUchida、WUV、WLAB公式；WHunter1和WC/V公式表现最差，与视觉评价结果在0.05置信水平下不相关。由表8结果可知：WHunter2公式预测性能最好，稍优于WGrum、WCIE10和WGanz，显著优于WUchida、WUV、WLAB、WHunter1、WC/V；WHunter1和WC/V预测性能最差，其中WC/V显著劣于WHunter1之外的其他7个公式。

3.2 基于类别判定法评价白度公式

基于类别判定法的实验数据，采用Spearman-r、Pearson-ρ进行白度公式预测性能的检验，线性拟合85个样品的ΔV与ΔW，r表示相关系数，相关系数越大，二者之间的相关性越好，反之则越差，结果见图5。可初步判定WHunter1和WC/V表现较差，远离趋势线；WHunter2、WCIE10、WGrum、WGanz公式表现较好，其数据点分布较为集中，靠近趋势线。

图5 类别判定法85个样品的视觉白度差ΔV与计算白度差ΔW的比较Fig.5 Comparison of visual whiteness difference ΔV and calculated whiteness difference ΔW of 85 samples by category judgment method

从Pearson-r来看，WHunter2的r最大，然后是WCIE10、WGrum、WGanz；接着是WUchida、WUV、WLAB；最后是WHunter1和WC/V。WHunter1和WC/V公式的相关系

数分别为0.419和0.028，与目视评价相关性较弱和基本不相关。从Spearman-ρ值来看，WHunter2的数值最大，其次是WCIE10和WGanz；接着是WGrum和WUchida；然后是WLAB和WUV，最后是WHunter1和WC/V。WLAB和WUV的相关系数ρ分别为0.674和0.657，预测性能较弱；WHunter1和WC/V预测性能最差，而WC/V基本不相关。2种方式对白度公式评价结果基本一致，结合2种方式的排名依次为：WHunter2>WCIE10>WGrum=WGanz>WUchida>WLAB=WUV>WHunter1>WC/V。

3.3 综合评价

综合2种评价结果来看，WHunter2白度公式具有最佳的预测性能，无论哪种视觉评价方法和指标，WHunter2白度公式预测性能都是最好的；然后是WCIE10和WGrum；WGanz和WUchida稍逊于前几名；WUV和WLAB具有类似的预测性能，在使用类别判定法时，相关系数有较大幅度下降；WHunter1和WC/V的评价效果最差，甚至不能正确表征物体表面白度。按照预测性能从优到劣依次为：WHunter2>WCIE10>WGrum>WGanz>WUchida>WUV=WLAB>WHunter1>WC/V。

4 Hunter白度公式分析

出乎意料的是WHunter2公式对非荧光织物的白度预测性能最好。事实上，WHunter2公式原本是用于评价荧光物品的白度，前期研究意外发现其评价荧光织物的效果很好且明显优于晚于其颁布的国际标准CIE白度[13]，在本文研究中尝试采用了非常规方法，将原适用于评价荧光白的WHunter2公式用于评价非荧光白织物。

WHunter公式是Hunter先生1958年基于HunterLab颜色空间采用色差概念设计[25]，后经优化标准白的色度坐标而逐步确立的，其具体形式[24]为

W=100-{(100-L)2+

式中：L为明度指数；a、b和ap、bp分别样品和标准白的色度指数；K1为常数，一般取1。原则上，样品不带荧光时，ap、bp分别取0.00、0.00；样品带有荧光时，ap、bp分别取3.5、-15.87。

在本文研究中，将公式原定义适用于不带荧光试样的公式(其中ap=0.00，bp=0.00)命名为WHunter1；将适用于荧光样品的公式(其中ap=3.5，bp=-15.87)命名为WHunter2，以便区分。分析WHunter2公式预测非荧光织物依然最好的原因如下：观察者在对白色物品进行白度视觉评价时，本就不按照荧光和非荧光先分类再评价，而是自然而然将样品与自己心里的标准白或理想白进行比较；人们通常认为样品偏蓝显得更白，本实验招募的观察者均来自纺织领域，对蓝白的喜爱程度可能更为显著，因此，采用偏蓝的理想白(ap=3.5，bp=-15.87)的WHunter2公式对非荧光织物的白度预测能够获得满意的效果也就合情合理了。

5 结 论

基于成对比较和类别判定的心理物理学视觉实验方法，分别对28块和85块涤纶白色织物进行视觉评估，评价9个白度公式的预测性能。得出以下主要结论。

1) 采用成对比较法评价非荧光织物，WHunter2预测性能最好，稍优于WGrum、WCIE10和WGanz，显著优于WUchida、WUV、WLAB，WHunter1和WC/V表现最差；采用类别判定法评价非荧光织物，WHunter2公式表现最好，WCIE10和WGanz次之，再依次是WGrum、WUchida、WLAB、WUV，WHunter1和WC/V评价效果最差。

2) 2种心理物理学实验方法对9个白度公式的评价结果基本一致，从优到劣综合排序为：WHunter2>WCIE10>WGrum>WGanz>WUchida>WUV=WLAB>WHunter1>WC/V，其中WC/V与视感白度基本不相关。

3) WHunter公式中原定义适用于荧光样品的WHunter2公式在评价非荧光样品时依然展示了优良的预测性能，后续亦会对WHunter2公式进行更深入的研究。