风速与风电功率波动概率分布建模
王金锋 姜炎君 温 栋 孙晓晨 任正某
(1.国网陕西省电力有限公司经济技术研究院,陕西 西安 710065;2.国网陕西省电力有限公司铜川供电公司,陕西铜川 727000)
0 引言
风力发电目前已成为最具开发前景的新能源发电方式,但由于风电出力的随机性与不确定性,风电在贡献力量的同时也给电力系统带来了各种新的问题和挑战,如风电出力波动带来的冲击,会导致电力系统电压失稳,电能质量下降,造成系统的继电保护设备发生误动[1]。为解决上述难题,研究风电的波动规律至关重要,在此基础上,科学规划风电并网,制定合理的运行方案,将有助于提高电网对风电的消纳能力。
现阶段,国内外相关学者对风速波动和风电功率波动进行了一定的研究。在风速波动特性分析方面,文献[2]基于电力系统的实时调度与优化控制需求的视角,研究了风速的瞬时波动特性和不确定性模型;文献[3]表明水平风速和竖直风速均具有多重分形特性,但有着不同的波动结构;文献[4]基于风电场动态时空关系建立风速分布模型;文献[5]利用波动模型完成了对风速序列波动特征的分析,并用SV模型刻画出了风速时间序列的变化特性。
在风电功率波动特性分析方面,文献[6]中采用带移位因子与伸缩系数的t分布(t Location-Scale)来描述风电功率波动特性的概率分布;文献[7]引入3个量化指标分析风电功率的波动特性;文献[8]从概率统计方法和时间序列方法两方面分析风电输出功率的波动特性;文献[9]分析了不同时间尺度下的风电功率波动特性;文献[10]研究了基于混合分布模型的风电功率波动特性;文献[11]从相关性和平滑性两个方面研究了不同时空尺度下风电出力波动性的统计学规律,并提出基于混合高斯分布进行概率分布分析;文献[12]提出一种基于非参数核密度估计的风电功率波动性概率密度建模方法;文献[13]建立了刻画风电功率波动特性的指标体系,然后在不同时间尺度下分析波动特性。
综上所述,现阶段国内外学者对风速和风电功率波动有一定的研究,但在定量描述波动特性方面较为缺乏,尤其是对于风速波动描述较少。
本文用概率统计的方法研究不同时间窗口下风速和风电功率波动的概率特性,作出不同季节下风速和功率波动量的概率密度直方图,用正态分布、t Location-Scale分布、Logistic分布、stable分布对直方图进行拟合,选取适合的分布对其进行定量描述。
1 几种概率分布形式
本文涉及的正态分布、t Location-Scale分布、Logistic分布对应的概率密度函数如公式(1)~(3)所示;stable分布没有统一的、封闭的概率密度函数表达式,但当其特征函数满足公式(4)时,则服从stable分布。
正态分布函数关系:

t Location-Scale 分布函数关系:
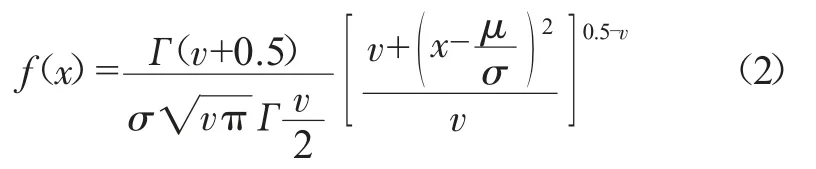
Logistic 分布函数关系:

stable 分布函数关系:
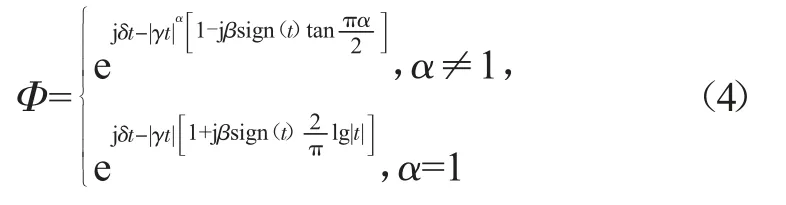
2 风速与风电功率波动量概率分布模型
选择风速波动的波动量Δvt和风电功率波动量ΔPt分别作为衡量风速波动概率和风电功率波动概率分布特性的指标,具体如式(5)和(6)所示:

式中:vt+1、vt与Pt+1、Pt分别表示t+1时刻、t时刻的风速与功率。
采用正态分布、t Location-Scale分布、Logistic分布、stable分布按季节(春季3月—5月、夏季6月—8月、秋季9月—11月、冬季12月—次年2月)分别对我国沿海某风场近五年实际运行数据中的风速波动量、风电功率波动量的概率直方图进行拟合,并对拟合结果进行分析。
2.1 风速波动量概率分布
图1为五年风速波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=-1.52×10-5,方差σ2=0.173;t Location-scale分布拟合曲线位置参数μ=-5.86×10-5,形状参数v=164.37,尺度参数σ=0.413;Logistic分布拟合曲线参数μ=-1.46×10-4,σ=0.239;stable分布拟合曲线参数α=1.993,β=0.404,γ=0.292,δ=-0.001。

图1 五年风速波动量概率分布拟合
由以上数据可得,风速波动量概率分布的四种分布曲线拟合状况都近似于正态分布,但在图线拟合上可以观察得到:风速波动量的概率分布更加符合参数μ=-1.46×10-4,σ=0.239的Logistic分布。
图2为五年春季风速波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=-6.11×10-4,方差σ2=0.184;t Location-scale分布拟合曲线位置参数μ=-7.70×10-4,形状参数v=206.78,尺度参数σ=0.426;Logistic分布拟合曲线参数μ=-0.002,σ=0.246;stable分布拟合曲线参数α=1.990,β=1,γ=0.301,δ=-0.005。
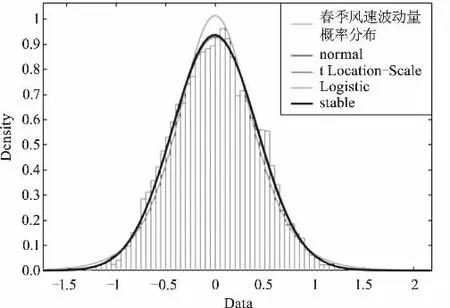
图2 春季风速波动量概率分布拟合图
由以上数据可得,春季风速波动量概率分布的四种分布曲线拟合状况都近似于正态分布,由其他三种分布可知,该概率分布并不对称,风速波动量均值小于0,但在大于0的部分存在厚尾现象,分析图线拟合情况得到:春季风速波动量的概率分布更加符合参数μ=-7.70×10-4,v=206.78,σ=0.426的t Location-Scale分布。
图3为五年夏季风速波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=1.43×10-4,方差σ2=0.175;t Location-scale分布拟合曲线位置参数μ=9.00×10-5,形状参数v=464.44,尺度参数σ=0.417;Logistic分布拟合曲线参数μ=-0.001,σ=0.241;stable分布拟合曲线参数α=1.991,β=1,γ=0.294,δ=-0.004。

图3 夏季风速波动量概率分布拟合图
由图可知,Logistic分布与实际相差较大,其他三种分布的拟合曲线都贴近风速波动量的概率分布直方图,但不能完整拟合风速波动量概率分布峰值,除正态分布外,其他三种分布也以0为中心对称分布,且分布状况极为类似,因此,Logistic分布能较好地拟合夏季风速波动量概率分布情况。
图4为五年秋季风速波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=3.608×10-4,方差σ2=0.164;t Location-scale分布拟合曲线位置参数μ=1.89×10-5,形状参数v=-0.074,尺度参数σ=-2.407 5×10-9;Logistic分布拟合曲线参数μ=4.22×10-4,σ=0.235;stable 分布拟合曲线参数α=2,β=0.649,γ=0.286,δ=4.54×10-5。

图4 秋季风速波动量概率分布拟合图
由以上数据可得,四种分布拟合平均值均近似于0,且有stable的特征指数α=2,stable分布退化为正态分布,但其拟合方差小于正态分布拟合方差。与春、夏季风速波动概率分布相比,秋季风速波动概率分布方差较小,即秋季风速波动量更加集中在0附近,风速波动表现为波动更平缓,以小幅度波动为主。
图5为五年冬季风速波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=5.56×10-7,方差σ2=0.172;t Location-scale分布拟合曲线位置参数μ=3.92×10-4,形状参数v=48.64,尺度参数σ=0.405;Logistic分布拟合曲线参数μ=8.29×10-4,σ=0.238;stable 分布拟合曲线参数α=1.99,β=-0.632,γ=0.291,δ=7.53×10-5。冬季风速波动量概率分布拟合中,t Location-Scale分布拟合与正态分布拟合有较大差异,Logistic分布拟合更符合实际情况。

图5 冬季风速波动量概率分布拟合图
2.2 风电功率波动量概率分布
图6为五年风电功率波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=-8.26×10-4,方差σ2=62.93;t Location-scale分布拟合曲线位置参数μ=-0.067,形状参数v=1.90,尺度参数σ=3.73;Logistic分布拟合曲线参数μ=-0.053,σ=3.77;stable分布拟合曲线参数α=1.31,β=0.007,γ=3.17,δ=-0.074。相比于风速波动量的概率分布,风电功率波动量的概率分布更加集中,在图像上表现为更加尖锐,波动量集中在-20到20的区间内,波动量超过此区间的概率仅有不到3%。

图6 五年风电功率波动量概率分布拟合
就图像拟合的结果而言,正态分布和Logistic分布对功率波动量概率的拟合并不理想,拟合结果方差偏大,图线较风电功率概率分布直方图更加宽矮,不能对风电功率波动量概率集中的状况进行准确地描述,而t Location-Scale分布拟合结果较好,拟合图线贴合准确。
图7为五年春季风电功率波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=-0.028,方差σ2=81.01;t Location-Scale分布拟合曲线位置参数μ=-0.022,形状参数v=2.74,尺度参数σ=5.46;Logistic分布拟合曲线参数μ=-0.007,σ=1×10-5;stable 分布拟合曲线参数α=1.54,β=0.035,γ=4.51,δ=-0.279。与总体风电功率概率分布相比,春季风电功率波动量的概率分布更加分散,在数据上表现为几种分布拟合的方差变大,但正态拟合分布曲线、Logistic分布拟合曲线与概率直方图的边缘拟合依旧较差,t Location-Scale分布拟合曲线与stable分布拟合曲线对概率直方图的边缘拟合较好,尤其是t Location-Scale分布拟合曲线能够表示风电功率波动量的概率分布特征,因此认为春季风电功率波动量的概率分布服从位置参数μ=-0.022,形状参数v=2.74,尺度参数σ=5.46的t Location-Scale分布。

图7 春季风电功率波动量概率分布拟合
图8为五年夏季风电功率波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=-0.005,方差σ2=61.43;t Location-Scale分布拟合曲线位置参数μ=-0.080,形状参数v=2.51,尺度参数σ=4.33;Logistic分布拟合曲线参数μ=0.06,σ=3.74;stable分布拟合曲线参数α=1.51,β=0.019,γ=3.62,δ=-0.093。夏季风电功率波动量较为集中,方差较小,从图像上可以看出t Location-Scale分布拟合曲线能够更好地贴合功率波动量概率分布直方图,因此认为夏季功率波动量概率分布符合位置参数μ=-0.080,形状参数v=2.51,尺度参数σ=4.33的t Location-Scale分布。

图8 夏季风电功率波动量概率分布拟合
图9为五年秋季风电功率波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=0.003,方差σ2=43.81;t Location-Scale分布拟合曲线位置参数μ=-0.082,形状参数v=2.22,尺度参数σ=3.49;Logistic分布拟合曲线参数μ=-0.066,σ=3.20;stable分布拟合曲线参数α=1.42,β=0.014,γ=2.93,δ=-0.094。秋季风电功率波动量的拟合曲线方差为四个季节中方差的最小值,即秋季的风电功率波动稳定性最好,且秋季风电功率波动量的概率密度直方图与tLocation-Scale分布拟合曲线贴合得更好,风电功率波动量概率分布符合位置参数μ=-0.082,形状参数v=2.22,尺度参数σ=3.49的t Location-Scale分布。
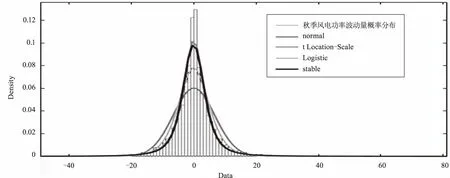
图9 秋季风电功率波动量概率分布拟合
图10为五年冬季风电功率波动量数据的概率密度分布及其四种分布拟合图线,图中正态分布拟合曲线参数为均值μ=0.001,方差σ2=63.07;t Location-Scale分布拟合曲线位置参数μ=-0.091,形状参数v=2.19,尺度参数σ=4.27;Logistic分布拟合曲线参数μ=-0.061,σ=3.93;stable分布拟合曲线参数α=1.39,β=0.025,γ=3.58,δ=-0.11。从图中可以看出,t Location-Scale分布对冬季风电功率波动量概率分布的拟合最好,因此认为冬季风电功率波动量概率分布符合位置参数μ=-0.091,形状参数v=2.19,尺度参数σ=4.27的t Location-Scale分布。

图10 冬季风电功率波动量概率分布拟合
3 结论
本文分别利用正态分布、t Location-Scale 分布、Logistic分布、stable分布对风速波动量概率密度和风电功率波动量概率密度进行拟合,结果显示:
(1)风速波动量和风电功率波动量均关于0值对称,整体而言,风速波动概率较符合Logistic分布;而风电功率的波动概率具有显著的高集中度特征,更加符合t Location-Scale分布。
(2)在不同季节的时间窗口下,风速波动量的概率分布稍有不同:春季,风速波动概率分布更符合t Location-Scale分布;秋季,风速波动概率分布更符合stable分布;夏季和冬季,风速波动概率分布更符合Logistic分布。
(3)在不同季节的时间窗口下,风电功率的波动概率分布均更符合t Location-Scale分布,没有体现出差异性。

