海上火箭热发射过程中发射平台耦合运动响应分析

王 阳 王宝来 刘大辉 王照洋 滕 瑶 王寿军 张 池

（1.烟台哈尔滨工程大学研究院 烟台264000；2.中集海洋工程研究院有限公司 烟台 264000）

0 引 言

自我国首次海上发射[1]成功以来，采取的方式均为冷发射，即先于海上发射平台弹射后进行二次点火。相比于冷发射，热发射拥有很多优点，如发射系统相对简单以及单位体积下安装的有效载荷更多等，但也会因为热发射火箭重量大、对发射平台或发射装置冲击作用较大，对平台尤其是海上发射平台运动特性要求更高。虽然海上发射构想的提出和实验研究已经有很多年，但目前海上发射尤其是海上热发射系统并不成熟。最早于1964年开始，就有意大利与美国联合研究并在肯尼亚某平台发射过多次航天器[2]；1988年，日本运输巨商三九和三菱重工业两公司联合设想的海上发射火箭装置取得美国专利权[3]；1995年，美、俄、乌、挪四国合作成立了海上发射公司——Sea Launch,并于1991年开始共发射火箭29 枚，3 次未成功，最终因经济等各方面原因宣布公司解体并由俄罗斯收购“奥德赛”海上发射平台[4]；自2019年我国第一次海上发射成功后，标志着我国成为第一个拥有完整海上发射技术并成功完成海上发射的国家，美国的SpaceX 公司也在2020年宣布即将实现“星链”部分的海上发射[5-7]。

燃气尾流数值方面研究技术发展迅速，尤其随着计算机的快速发展，国内外研究成果均日渐成熟。如VENKATAPATHY 等[8]对燃气尾流进行了模拟并采用自适应网格的方法提高了燃气射流流场的精度，VU 等[9]对燃气尾流冲击时刻喷水降温效果进行了模拟分析，国内傅德彬、马艳丽等[10-12]多次对燃气尾流相关问题进行实验模拟对比研究。国内海上发射相关领域文献较少，如2019年殷金龙[13]对海上发射领域的稳定平台的分析，设计了两自由度的液压稳定平台；2020年宋远华[14]重点讨论了大马力拖轮为海上发射平台抛起锚精准定位问题以及安全举措;2021年俞俊等[15]对海上发射平台冷发射冲击载荷下发射船的运动响应研究，基于三维势流理论通过施加短时集中力考察了发射船不同吃水以及发射相位下的船体运动响应。

海上热发射因火箭重量大以及发射期间火箭与发射平台会发生双向耦合作用，尤其发射平台的运动响应看似微小的运动都会影响火箭的姿态控制精度。本研究以长165 m、宽40 m 的某型号海上发射船船体为发射平台，基于三维势流理论，提取尾流冲击载荷后，对发射平台进行频域分析以及尾流冲击载荷、风浪流联合作用下的时域分析，并对比分析了发射船的RAO 响应。计算模拟过程为了方便尾流冲击载荷的提取，提出了1 种海上热发射冲击载荷简化计算的方法，可提取关于尾流载荷的时历曲线以便于后续海上发射平台的研究分析。

1 计算理论

1.1 湍流模型

湍流模型采用Realizablek-ε湍流模型[16]，在高雷诺数条件下以涡量均方值波动的动力方程为基础对湍流动能耗散率输运方程进行修正。并且改进了涡黏性表达式，使其满足雷诺应力的数学约束条件，确保雷诺正应力恒为正，湍流剪切应力满足于施瓦茨不等式。

1.2 三维势流理论

势流理论假定速度势的存在，并且满足拉普拉斯方程和四类边界条件：自由面条件、物面湿表面条件、海底条件和辐射条件（无穷远处边界条件）。由拉普拉斯方程和边界条件确定唯一速度势，得到速度分布，之后结合伯努利方程计算得到湿表面的分布压力，最后沿物体的湿表面积分得到压力的合力。

当入射波波长远远大于波高时，可把总的速度势φ[17]分为辐射势和绕射势：

式中：ξj指刚体假定下物体六自由度运动的幅值；φj为单位辐射势；φ2表示物体固定在原位置时引起的对入射波的扰动；φ1为入射波速度势。

式中：g为重力加速度，m/s2；β为入射波的方向角，°；H为水深，m；v是色散关系的实根。

通过求解在确定的边界条件下的拉普拉斯方程，从而求解流场中的辐射速度势和绕射速度势。

2 计算模型

2.1 燃气尾流模型

考虑采用某型号火箭发动机喷管进行火箭燃气尾流计算。为更好地模拟燃气尾流的数值，过程中使用动网格技术，可以按照火箭基本的运动规律，也可以在每一次全流场区域求解后，通过求解得到的燃气尾流流场参数，采用欧拉法求解当前计算时刻边界的运动规律，然后根据新得到的计算区域更新网格。图1为拉瓦尔喷管及其动网格定义区域网格划分，采用六面体核心网格，最小网格尺寸设置为2 mm,最大网格尺寸设置为25 mm,增长率设置为1.10，边界层数为10，通过手动调节的方式细化拉瓦尔喷管的网格。

图1 拉瓦尔管模型及网格划分

动网格技术采用自编译UDF 方式，主要用到Fluent 的两个宏函数，分别是DEFINE_CG_MOTIN和DEFINE_EXECUTE_AT_END。前者是用来指定火箭运动边界的运动参数，即从上一个函数得到的运动物理量可通过这一函数反应到运动边界上；后者是通用宏函数，在稳态求解时，这一宏函数在每一个迭代步结束的时候开始执行，而在非定常求解时，则在每个时间步结束的时候执行，所以可以通过这一宏函数求解出流场内的每个迭代步（时间步）所需要的物理量。

图2为简化火箭燃气尾流整体计算区域模型，拉瓦尔管正下方80 cm 处设置简化模拟 6 m×6 m 的钢板代替发射平台甲板以方便提取尾流冲击数据（因主要讨论整体区域冲击压力，故简化导流器）。为提高计算精度，计算区域网格划分为两部分分别计算：拉瓦尔管及其运动区域考虑采用非结构化网格，网格大小的精度已在上述段落进行描述；外流域包括甲板部分采用结构化网格进行计算，为了与非结构化网格进行过渡，网格尺寸设置为25 mm。综合各方面考虑计算精度以及运算量，控制方程的离散格式选择一阶迎风离散格式。边界条件设置中，拉瓦尔喷管入口设置为压力入口，外流场4 个面设置为压力出口，拉瓦尔喷管进行物理学抑制，其他面均设置为壁面，整体计算域划分网格总数约为310 万个。

图2 燃气尾流计算区域

2.2 水动力模型

发射平台使用某新型火箭发射船，其船型为165 m 自航甲板驳船。图3为发射船体水动力模型，网格精度为10 mm，船体网格划分总数为 29 512 个。表1为发射船主要尺度参数。

图3 发射船水动力模型

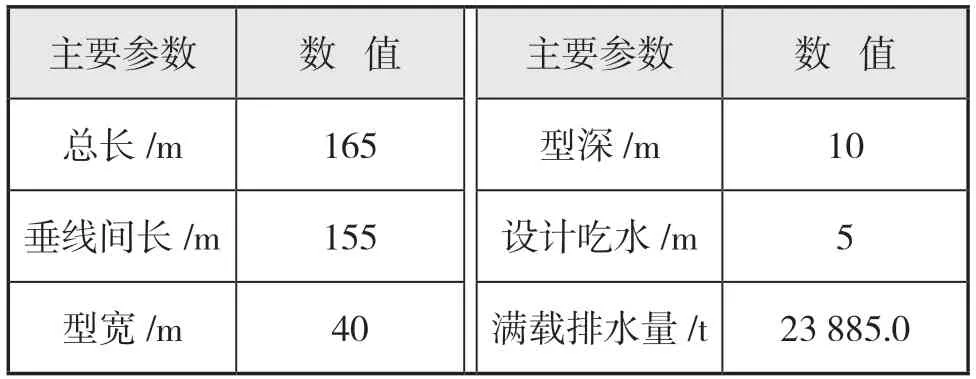
表1 发射船主尺度参数

3 发射船在发射过程中的运动响应分析

3.1 火箭尾流冲击载荷分析

火箭尾流冲击载荷模拟边界条件初步采用压力入口总压为9 MPa,温度为3 200 k；压力出口边界条件采用标准大气压即压强为10 325 Pa,温度为293.15 k，计算时间步长为1×e-3，时间步数设置为3 000。图4至图12分别为0.016 s、0.2 s、1.5 s 时刻的压力、温度流场迹线以及湍流强度云图，由于相对于喷管入口压力来说喷管出口的压力小得多，冲击底部监测压力变化均在2 MPa 以内，对于不同时刻的压强流场迹线图对比并不明显。可以看出不同时刻温度流场迹线图和湍流强度云图对比明显，不同时刻压强流场迹线0.016 s 时刻尾流冲击底部中心瞬时温度达到3 300 k；0.2 s 时刻尾流冲击底部平均温度开始减少，瞬时湍流强度占比也在此时达到最大湍流强度占比；1.5 s 时刻尾流冲击底部瞬时温度已降到1 492 k，此时的高湍流占比已低于0.016 s 时刻。根据以上分析可以得出，不同时刻尾流冲击底部压强、温度和湍流强度均在 0.2 s 左右达到峰值，之后随着喷管上升上述各参数开始下降，直到1.5 s 拉瓦尔喷管对底部甲板冲击作用已极其微小。

图4 0.016 s 压强流场迹线图

图5 0.2 s 压强流场迹线图

图6 1.5 s 压强流场迹线图

图7 0.016 s 温度流场迹线图

图8 0.2 s 温度流场迹线图

图9 1.5 s 温度流场迹线图

图10 0.016 s 湍流强度云图

图11 0.2 s 湍流强度云图

图12 1.5 s 湍流强度云图

为了进行不同体量的火箭尾流对海上发射平台载荷冲击的影响对比，进行压力入口温度分别为工况一（9 MPa、3 200 k）以及工况二（13 MPa、3 500 k）,压力出口等其他初始条件保持不变。在使用软件Fluent 的基础功能上，为了提取一定面积内火箭上升过程中对发射船的冲击力，对模拟甲板上表面进行一定范围的矩形面积内压力检测，并进行面积加权平均积分计算，见式（6）。经计算后得到冲击压力的面积加权平均积分，乘以相应面积，最终可以得到等效载荷，方便下一步发射平台的运动响应计算。

两种边界条件的计算结果经过对比后，可得如图13所示对应等效载荷计算时历曲线。

图13 等效尾流冲击载荷时历曲线

首先，对应不同压强和温度下对甲板的冲击作用时间历程趋势基本相同，均为毫秒级冲击，趋势为短期内压力迅速增加并达到峰值；而后，随时间以及飞行高度的上升，冲击载荷开始减少并逐渐趋向平稳阶段。压力入口为9 MPa 条件下，冲击载荷面积加权平均压强最大值为0.298 MPa，压力入口为13 MPa 条件下，冲击载荷面积加权平均压强最大值为0.399 MPa，且达到峰值所需时间以及整体趋势比前者延迟0.02 s。以上为火箭冲击载荷计算结果对比分析，可为下一步对发射船的加载作 准备。

3.2 海上发射船的运动响应分析

3.2.1 海上发射船的水动力分析

波浪作用下的运动响应可由幅值响应算子进行描述，基于三维势流理论，对于海上发射船进行一系列水动力分析。三维空间中，浮体可以进行 6 个方向的运动，分别是线位移方面的纵荡（Surge）—沿x轴方向的位移、横荡（Sway）—沿y轴方向的位移、垂荡（Heave）—沿z轴位移；角位移方面的横摇（Roll）—绕x轴转动角度、纵摇（Pitch）—绕y轴转动角度以及艏摇（Yaw）—绕z轴转动角度[18]。

模拟主要考虑海上发射过程中的垂荡、横摇、纵摇以及艏摇4 个方面的运动，以分析不同来浪角度下以上自由度的运动响应以及为后续海上发射船和火箭双向耦合运动提供参考。选取单位波幅下规则波的周期范围为 2～60 s，并且在运响应较大值附近进行加密。考虑到主船体的对称性，选取 0°～180°内的浪向，间隔 15 °，共13 个。

图14至图17为发射船横摇、纵摇和艏摇对于不同浪向角的RAO 响应。随着规则波周期的增加，发射船垂荡RAO 对于不同浪向角其变化为整体上升趋势，均在7～9 s 附近出现极大值，90°的浪向为极大值1.4°，9 s 过后均趋向于1°并保持水平。

图14 垂荡运动RAO

图15 横摇运动RAO

图16 纵摇运动RAO

图17 艏摇运动RAO

由图14至图17可见，发射船横摇、纵摇及艏摇对于不同浪向角的RAO 响应，其变化随规则波周期增加均表现为先上升后下降，且峰值均出现在8 s 附近。

以上为对海上发射船的4 个方向的水动力分析，因为发射船尺寸足够大，所以在大多数情况下运动响应不会太大，具有很好的耐波性，可以为海上发射提供一个良好的载体平台。

3.2.2 海上发射船时域耦合响应分析

（1）环境参数

为了避免海况分析的单一性以及对海上发射要求的条件响应，考虑进行2 种海况下的时域分析，如表2所示。

表2 环境参数表

（2）风流力系数定义

风流载荷通常可以用式7 和式8 进行表达，且AQWA 中的风流力系数定义为不涉及速度的的项，即：

式中：ρ为海水/空气的密度，kg/m3；Cd为流力/风力系数；A为迎流/迎风系数；β为迎流/风面积与流/风的方向的相对角度。

（3）系泊设置

初步设置海上发射船采用4×1 的系泊布置方式。系泊缆共4 根，分为4 组，朝向每个象限的45°方向进行布置，导缆孔与锚点之间的水平跨距均为850 m,具体布置方式如图18所示。系泊缆为单一成分缆，材质为120 mm 钢芯钢缆。

图18 系泊缆布置方式

（4）冲击作用下的时域耦合分析

在海况1、2 的环境条件下，选取火箭发射尾流冲击分析中载荷较大者（压力入口边界条件为13 MPa）进行加载，模拟计算时间步长为0.01 s,总模拟时间为100 s,迭代时间步为10 000 步，尾流冲击加载时间设置为25 s 时刻且尾流总作用时间为5 s，随机入射波采用JONSWAP 谱。

图19至图22所示为对垂荡、横摇、纵摇以及艏摇运动的峰值结果进行的提取以及对比。

图19 垂荡运动结果对比

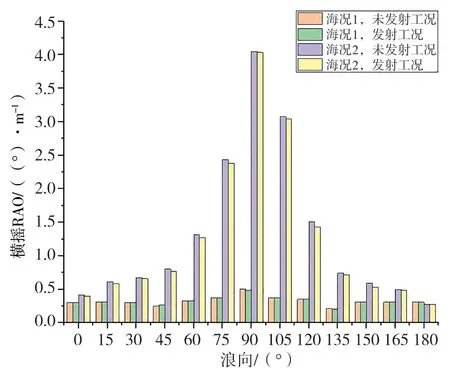
图20 横摇运动结果对比

图21 纵摇运动结果对比

图22 艏摇运动结果对比

分析可知，多因素耦合作用下，垂荡方向的运动加载前后运动幅值明显增大，海况1 和海况2 对应运动整体趋势基本相同，均在浪向角90°时运动幅值最大，即从垂荡方向的运动幅值角度来说横浪状态时并不利于发射。从横摇方向的运动幅值对比来看，尾流的冲击载荷影响并不明显，影响因素更大者在于海况，虽然整体趋势上海况1 和海况2 的变化趋势相似，但海况2 的条件作用下，尤其在横浪90°时，横摇幅度达到了4.1°。此外，横摇、纵摇、艏摇在火箭的冲击载荷作用下，幅值变化并不明显，甚至从横摇和艏摇的角度来看，冲击载荷与风、浪、系泊等的联合作用下，抵消了一部分运动幅值，而纵摇方向没有明显的幅值变化。

（5）不同海况下发射平台受冲击作用对比

为了进一步清晰地探究箭体发射的冲击作用对不同海况下的海上发射平台运动响应的影响，根据上述运动响应分析垂荡、横摇、纵摇以及艏摇四自由度的峰值对比可知，0°～180°内四个自由度运动响应峰值的最小值和最大值分别对应0°和90°，下面分别对0°和90°浪向时，总历程中的24～50 s 四个自由度的运动响应进行分析对比。

图23至图26为0°浪向角对应的垂荡、横摇、纵摇以及艏摇四自由度运动响应幅值对比。通过对比分析可知海况2 环境下比海况1 环境下垂荡运动幅值略高，但相比发射前后，发射冲击作用比海况变化影响作用更大，且在海况2 环境下发射过后15 s 内垂荡运动幅值依然很高。从横摇角度，不论在哪种海况环境下，箭体的冲击作用影响不会太大，相同海况下，发射冲击作用均会使船体的横摇运动幅值增大0.05°，海况1、2 环境下，发射冲击作用时刻横摇运动响应峰值分别为0.2°和0.41°。对于纵摇运动响应，可以发现海况环境以及发射冲击作用都有不小的影响，但结合图19可知，0～100 s 船体时域响应模拟过程中，纵摇最大值都不止出现在火箭发射前后。从艏摇的角度来看，整体趋势上，海况2 环境下的艏摇运动幅值大于海况1 环境下艏摇运动幅值；除此之外，2 种海况下，发射时刻发射工况的艏摇运动幅值大于未发射工况，发射过后（约33 s 后）出现转折点，即发射工况下的艏摇运动幅值小于未发射工况下的艏摇运动 幅值。

图23 0°垂荡运动结果对比

图24 0°横摇运动结果对比

图25 0°纵摇运动结果对比

图26 0°艏摇运动结果对比

图27至图30为90°浪向角对应的垂荡、横摇、纵摇以及艏摇四自由度运动响应幅值对比。通过对比分析可知90°浪向角工况下即横浪状态下，海况环境与发射冲击均对垂荡运动响应和纵摇运动响应产生不小的影响，海况2 环境下发射状态垂荡和纵摇运动幅值分别达到了1.35 m 和1.38°。从横摇和艏摇角度，影响更大的是海况的环境变化。相对于0°浪向时域响应分析，海况2 环境下，发射状态的横摇运动响应峰值比海况1 环境下的横摇运动响应峰值高3.3°，对应的艏摇运动响应峰值也高出0.45°。

图27 90°垂荡运动结果对比

图28 90°横摇运动结果对比

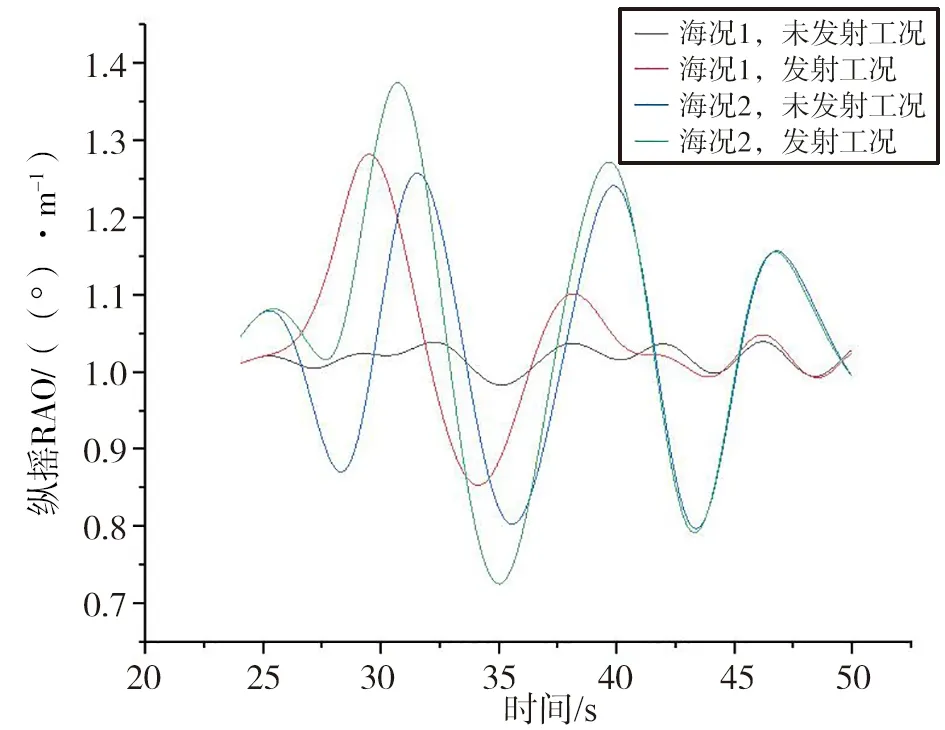
图29 90°纵摇运动结果对比

图30 90°艏摇运动结果对比

综合以上对比分析，更加说明从各方面船体运动响应角度来看，发射平台的横浪状态不利于火箭热发射。

4 结 语

本文基于三维势流理论，考虑了箭体对船体的冲击作用以及风浪等环境因素，对计算结果总结如下：

（1）通过垂荡、横摇、纵摇以及艏摇4 个方向的对比可知，首先应选择在三级及以下海况环境进行海上发射，更有利于火箭和海上发射平台的双向安全；此外，区别于未发射工况的运动响应变化，海上平台热发射在火箭尾流的冲击下，不仅在发射时刻，在耦合作用下，发射过后的运动响应依然明显；最后，应避免发射平台横浪时进行发射。

（2）火箭的发射方式考虑采用热发射，提供了一种海上发射工况下尾流冲击的简易计算方法，即利用面积加权平均积分的方法对一定范围内的压力进行等效计算，可为船体结构强度以及运动响应等分析提供冲击载荷的时历曲线。

（3）通过以上对比分析可知此船稳性较好，可满足多次海上发射作业的需求。考虑到着重提取火箭对船体的冲击作用，故对计算模型进行了大量简化，忽略导流器等部件且采用了理想气体进行计算，发射船也只进行了水动力部分的运动响应计算。

后续将进行更加充分深入的对比分析，以期为海上发射平台的研究作出更多贡献。