码头系泊系统快速分析软件开发

时永鹏 闫凤超

（中国船舶及海洋工程设计研究院 上海 200001）

0 引 言

船舶系泊事故时有发生，系泊事故可能会造成结构损坏、缆绳断裂以及船舶状态的突变等。尤其发生缆绳断裂时，缆绳内部能量突然释放会造成缆绳快速回弹，极易造成人员伤亡[1-2]。因此系泊安全受到船东越来越多的关注，采取的措施包括标识缆绳反弹区、设置护栏以及进行系泊分析等，其中系泊分析是在详细设计阶段和系泊实施前可以完成的主要的系泊风险评估方式[3]。基于系泊计算、分析，可以对系泊设计进行评估、优化，也可以对船舶可承受的极限环境载荷进行预先判断。

规范计算是实船设计中最常用的系泊计算方法，常用的规范包括IACS REC.10[4-5]和各船级社规范。但规范计算方法过于简化，许多重要的系泊因素（包括船舶类型、码头条件、系泊布置以及缆绳材料等）都无法考虑在内，计算精度较低。

石油公司组织OCIMF 的出版物“MOORING EQUIPMENT GUIDELINES”（下文称为MEG，最新版为MEG4）中为液货船提供了更详尽的系泊分析指导和相关数据[6-7]，并被很多系泊分析方法借鉴，然而其并没有提供直接可用的系泊分析工具。

使用成熟的商业软件是目前最可靠的系泊分析方法，但不同的软件有不同的特点或适用性，如由法国船级社开发的Ariane 系泊分析软件，其计算方法可考虑风、浪、流等复杂的环境条件，适用于单点、多点和码头系泊等不同的系泊场景。然而该软件有较高的使用门槛，需要输入繁复的数据参数，易出错且计算过程也很耗时。如要完成一次多参数的方案优化，一般需要一周或更长时间，并且其计算原理也更适用于考虑波浪载荷的海工产品。

本文借鉴已有的系泊分析方法和软件，对码头系泊系统的组成及特性进行分析，实现1 套具有更低用户使用门槛、更高计算效率，且兼具准确性的码头系泊分析软件的开发。

1 码头系泊系统的组成

本文以码头系泊作为研究对象，系泊系统的形成过程是船舶、码头与环境的相互作用过程，因此本文将码头系泊系统分为环境系统、船舶系统和码头系统3 部分。为提高准确性，计算中需将各个系统中的重要因素纳入计算模型，但也需要结合开发目标进行合理简化。

1.1 环境系统

船舶可能受到的载荷种类非常丰富，包括常见的风、浪、流，以及潮汐、涌浪和船行波等，而船舶在不同系泊场景下需侧重考虑的环境因素也不同。

码头系泊一般位于遮蔽水域，环境因素较简单，其中规范和OCIMF 推荐的码头系泊环境因素如表1所示。

表1中，风速为高于地面10 m 处的30 s 内的平均风速；30 s 被视为系泊系统的平均响应速度。环境载荷从船尾指向船首时，其角度定为0°。

结合表1及实船设计经验，环境系统中仅考虑风和流，可以满足大部分船舶的码头系泊分析需求。此外，仅考虑定常的风、流载荷，简化环境系统，可提高系泊分析效率。

1.2 船舶系统

船舶系统主要包括船舶参数和船舶系泊，前者直接影响环境载荷的大小；后者影响系泊力的内部分配。

船舶系统的详细组成如下页图1所示，本软件将尽可能准确地对船舶系统进行描述。

图1 船舶系统的主要组成

1.3 码头系统

码头系统包括码头高度、码头缆桩布置、码头水深、码头碰垫的布置和物理性能等（见图2），其中码头布置影响系泊缆绳的实际长度和角度、码头水深影响环境载荷的大小、碰垫直接影响系泊力及船舶位移。本软件将尽可能真实地表达码头系统信息。

图2 码头系统示意图

2 系泊系统的数学模型

在定常环境载荷下，系泊力与环境力将达到平衡，系泊系统达到稳定状态；在稳定的载荷作用下，系泊系统可视为一个定常系统。本文将定常定义为一个相对的时间长度，是船舶在一定的环境载荷下，系泊系统与之达到平衡所需的时间。参照IACS REC.10 与MEG4 中的描述，该时间长度定为30 s；30 s 是一个足够短的时间段，允许我们将变化的外界环境离散为不同大小的定常环境的叠加，从而将码头系泊分析转变为定常分析。

当码头系泊系统中出现涌浪、波浪和船行波等不稳定因素时，系泊系统无法在短时间内达到稳定状态，一般需要针对特定的计算案例进行CFD 水动力分析并进行时域仿真计算，本文暂不考虑这种情况。

2.1 坐标系

本文中坐标系的定义如图3所示。假设船舶右舷靠泊码头，x轴正向为纵向向艏、y轴正向为横向指向左舷、z轴正向为垂向向上，力矩和角度都以逆时针为正。

图3 坐标系定义

本文中，全局坐标为基于码头的固定坐标系，局部坐标为基于船体的运动坐标系。在初始状态下，全局坐标与局部坐标有相同且以上文描述为基准的x、y、z的坐标轴方向；船体运动即局部坐标系在全局坐标系中的运动。

2.2 平衡方程

将船舶视为刚体，船舶运动存在6 向自由度。系泊系统达到平衡状态时，船体所受的合力为0。将船舶受力分解到6 个方向，分别为Fx、Fy、Fz、Mx、My及Mz，可形成6 个平衡方程。基于后文第2.6节论述，对船舶运动进行简化，简化后仅需3 个力平衡方程，即Fx=0、Fy=0 及Mz=0。

船体受到的力可以归类为缆绳力、碰垫力和环境力。由于每根缆绳长度、角度及位置不同，需单独计算每根缆绳的拉力及其在3 个方向的分力；碰垫力同样需要根据位置分别计算。将这些力叠加，形成平衡方程如下：

式中：n为缆绳的数量；m为碰垫的数量；FxiLine、FyiLine、MziLine分别为第i根缆绳在x、y以及z向的分力和力矩；FjFender、MzjFender代表第j个碰垫在y向和z向的力与力矩；同理，FxWind、FyWind、MzWind和FxCurr、FyCurr、MzCurr代表风和流在3 个方向的力和力矩。下文将对上式中的各个力分别进行分析计算。

2.3 环境力

环境力是环境与船体的作用结果。本文中环境载荷的计算使用MEG4 中的环境系数法。MEG4 基于大量的模型实验和计算流体力学软件分析、得到无因次化的风载和流载系数；该系数是环境载荷角度、水深吃水比、船型特征、船舶载况等的函数；环境系数再结合实际计算的风和流的速度、船舶主尺度、受风面积等参数，可计算得到环境载荷的 大小。

如以x方向的流载荷FXc的计算为例，其计算公式如下：

式中：ρc为水的密度，kg/m3；Vc为水流速度，m/s；LBP为船长，m；T为计算吃水，m。CXc为MEG4中提供的无因次化的流载系数，计算方法如下：

MEG4 中，函数fc通过图表的方式呈现。本软件通过读取图表数据、使用数值拟合和插值方法实现该函数的计算，可适应任意合理的用户输入。其他环境系数和环境载荷的计算同理，更多的计算方法和公式请参照MEG4 中的描述。

2.4 缆绳力

缆绳的位置、长度、角度及材质等因素都会影响其拉力大小。本软件中建立缆绳真实的三维空间模型，并定义其物理特性。实际系泊状态下，缆绳可能存在多个拐点，如典型的缆绳轨迹为“绞车-羊角滚轮-导缆孔-码头缆桩”，该4 点可确定缆绳的三维形状。计算模型中，缆绳的三维模型也通过一系列控制点描述，如：P0 表示缆绳在码头的固定点（码头缆桩）；P1 表示缆绳在船体的出口点（导缆孔）；P2、P3 代表缆绳在船上的控制点（羊角、带缆桩、绞车等）。可以发现：P0 在全局坐标系中的坐标不会变化，而P1、P2、P3 等在船体局部坐标系中的坐标不会变化；船体运动会导致P0 与P1 相对位置的变化，而船体上的点（P2、P3 等）的相对位置不会发生变化。

船体位移引起缆绳长度变化，在船体坐标系发生角位移θ和线位移(∆x,∆y)后，缆绳控制点P1（x,y）的新全局坐标为(x′,y′)，两者有以下关系：

根据P1 的新坐标，可计算缆绳的伸长量∆l及拉力FLine。伸长量与拉力的函数关系通过用户自定义的拉力-变形率函数体现，如下列公式中的函数f。

式中：MBL为缆绳的最小破断负荷；el为缆绳伸长率，即伸长量Δl与缆绳无拉力状态下的原始长度lLine的比值。由于缆绳仅能提供单向力，拉力-变形率函数在0 点一阶不连续。

此外，缆绳的初始拉力与尾索配置也会影响缆绳最终的拉力大小。

（1）初始拉力的影响

实船系泊时，会在系泊初始状态下，通过绞车或其他方式给予缆绳初始拉力。初始拉力可减小船舶在环境载荷下的运动，也可能降低缆绳的最大拉力，是一个重要的系泊参数。对应到计算模型中，船舶的初始状态应是环境载荷为0、缆绳的初始拉力与碰垫力达到平衡的状态。系泊计算的第一步必须基于用户给出的初始拉力，确定系泊的初始状态，包括船舶的初始位移及缆绳的初始变形。

（2）尾索的影响

当缆绳的刚度太大时，一些船舶可能会设置尾索以优化缆绳受力。由于主缆绳和尾索有不同的物理特性（即不同的拉力-变形率函数），在相同的轴向拉力下，两者有不同的变形率，可通过下列公式计算得到平衡状态下两者各自的变形。

式中：f代表缆绳的拉力-变形率函数；下标Line代表主缆绳，Tail 代表尾索。

2.5 碰垫力

碰垫在被压缩（与船体的接触点产生y向负位移）时，会对船体产生反弹力。对于码头系泊系统，风和流为离岸方向时，缆绳受力较大；风和流为向岸方向时，主要靠碰垫抵抗环境载荷。

碰垫反弹力与变形率也存在类似于缆绳变形的函数关系，本文不再详述；且该函数同样在0 点一阶不连续。碰垫仅会产生y向分力FFender，且始终为正；该力乘以碰垫的x向坐标可得到碰垫产生的z向力矩MzFender。

2.6 船舶运动的简化

船舶运动引起导缆孔位置变化，从而导致缆绳拉力变化。导缆孔作为船体上的一个点，具有三向运动自由度。可直观看出，导缆孔的x向和y向位移对于缆绳变形有显著的影响。本节通过分析导缆孔的z向位移引起的缆绳长度变化，反向推导船舶运动的影响。

船舶的升沉、横倾和纵倾会导致导缆孔的z向位移；同时，该三向运动也主要是使导缆孔产生z向位移。

（1）船舶的升沉

船舶所受的缆绳力、碰垫力和环境力中，只有缆绳力会产生显著的z向分力，造成船舶升沉。

MEG4 中推荐的缆绳水平夹角为15°，在不利的轻载载况下，建议不超过25°。以某5 万载重吨油轮为例，其配置缆绳16 根，其中倒缆4 根。假设缆绳的水平夹角为不利的25°，在MEG4 基准环境条件下，其缆绳拉力极值约为27 t，均值约15 t，16 根缆绳产生z向分力约为100 t。

该船轻载吃水的水线面积约为4 500 m2，在100 t 的z向压力下，升沉约20 mm；在25°水平夹角下，会导致缆绳约8.5 mm 的长度变化。缆绳长度平均约为30 m，其长度变化率约为2.8×10-4。对于MBL约为60 t 的常规纤维缆，其产生的拉力变化不足0.1 t，故船舶的升沉运动可被合理忽略。

（2）船舶的横倾与纵倾

风和流为90°时，船舶所受的横向（y向）环境力最大，作为考虑横倾影响的极端工况。

船舶轻载时，风载是主要环境载荷，流载约是其5%，且流载的横倾力臂很小。缆绳的y向拉力与风载基本相等，风载的力臂从上建到水面分布，可以认为风载与缆绳产生的x向力矩相互抵消，产生的横倾力矩可忽略，如下页图4所示。

图4 不同吃水下的船舶受力

满载吃水时，流载增大到风载的75%左右，且流载力臂增大、风载力臂减小，可认为两者产生的x向力矩大致抵消，横倾力矩主要由缆绳产生。假设缆绳的水平夹角为10°，同样以上述油轮为例，缆绳平均拉力为15 t，除去倒缆的缆绳数量为12根，导缆孔距水线约6 m，缆绳产生的x向力矩约为1×103量级。该船满载时，横倾1°所需力矩约为8×103量级，计算可得横倾引起的导缆孔z向位移约35 mm、缆绳长度变化约6 mm，由此表明横倾导致的缆绳拉力变化可忽略。

艏艉缆绳对船舶产生的纵倾力矩本身会相互抵消，同时船舶纵倾所需力矩显著大于横倾，类似方法分析得到，船舶纵倾的影响可忽略。

上述分析表明：导致导缆孔产生z向位移的船舶升沉、横倾和纵倾三向位移可以被合理忽略。值得注意的是，本节所述的船舶运动简化是在一定数量级上的分析，并非严谨推导。

3 软件开发及用户界面

本软件使用Visual Studio 环境和C#语言，完成系泊系统分析的算法实现和用户界面开发。算法实现保证计算效率和准确性，用户界面则应保证以较低的门槛引导用户快速、准确地输入必要的数据，并直观地输出计算结果。

按照上文所述的系泊系统划分方式，软件引导用户依次输入船舶、环境、码头、缆绳及系泊布置信息。

3.1 基本信息输入

（1）输入船型信息和主尺度信息，见图5。

图5 用户输入-船舶参数

（2）输入环境载荷见下页图6，用户可以批量设置需要计算的风和流的方向、以及在不同方向上的速度，软件会自动生成所有环境组合。

图6 用户输入-环境参数

（3）输入码头信息（见图7），含水深、码头高度和碰垫的物理特性。软件通过收集常用的碰垫数据信息，对不同尺寸碰垫的变形-弹力曲线进行回归，得到无因次曲线；用户输入典型变形下的碰垫弹力值，可自动生成碰垫的变形-弹力曲线。此外，软件也允许用户输入自定义的碰垫变形-弹力曲线。

图7 用户输入-码头参数

（4）输入缆绳信息（见图8），包括主缆绳与尾索的物理特性、缆绳MBL以及初始拉力。软件内置多种类型缆绳的物理特性数据库，用户可快速选择，也可通过输入参数、自由定义缆绳物理特性。软件会根据用户输入，绘制缆绳的拉力-变形率曲线图。

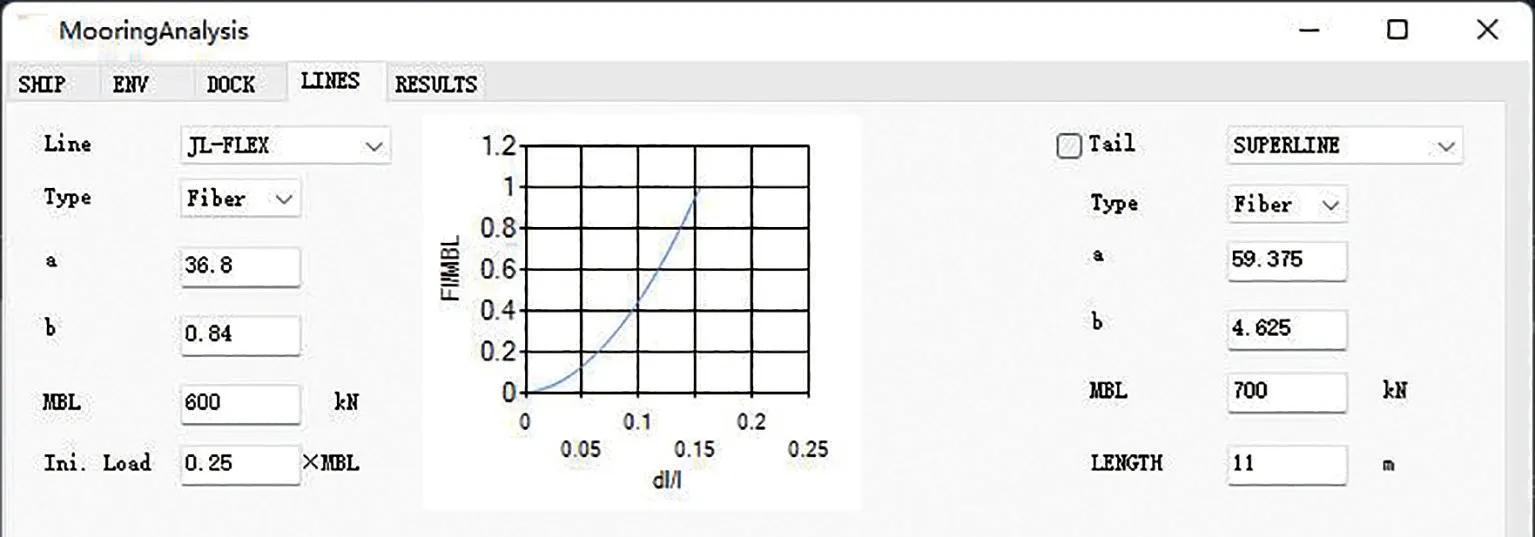
图8 用户输入-缆绳参数

此外，软件可将用户的所有输入另存为独立的系泊计算模型文件，方便保存与传输。

3.2 系泊布置信息

系泊系统的布置信息包括所有缆绳的三维控制点信息、码头碰垫和码头缆桩的布置信息，数据量较大，且在方案优化时需要频繁修改。

在常见的系泊软件中，需要用户读取系泊图纸并在软件中输入所有控制点的三维坐标，效率很低，尤其发生频繁的方案修改时，需要反复进行“图纸修改-读取坐标-修改软件输入”的流程，极易发生数据不同步的错误。

通过定义与CAD 绘图软件的标准接口，可将存储在CAD 图纸中的系泊布置信息直接读取至本软件，节省大量用户时间；系泊图纸发生修改时，其信息也会同步到本软件，保证数据一致性，并非常高效、准确地完成系泊设计的迭代优化。如下页图9展示的用于本软件输入的标准化系泊布置图纸，其形式与用于送审的系泊布置图纸基本一致。

图9 用户输入-系泊布置信息

3.3 软件输出

软件会直接输出所有环境和吃水组合工况的缆绳拉力极值，将其作为系泊设计的“Working Load Limit”，并根据缆绳材质计算“Ship design MBL” （“Working Load Limit”和“Ship design MBL”基于MEG4 中的定义）和缆绳最小破断负荷；同时还会输出计算的中间数据，用户可进一步进行数据分析，或挖掘规律进行针对性的系泊优化等，中间数据包括所有环境和吃水组合下，所有缆绳的受力大小、船体的位移和作用在船体上的环境载荷等，如图10所示。

图10 软件输出-部分输出数据

软件计算结果对于任何的输入修改都会即时响应，即本软件可实现从“设计输入 ”到“设计结果”的即时数据关联。

3.4 软件计算的准确性校核

本软件的计算结果经过多型船和多种系泊方案的计算验证，其计算结果与计算变量之间的影响关系符合一般的系泊规律，且经过与OCIMF 计算方法和Ariane 软件的计算结果进行对比，其计算精度可以满足使用要求。表2为多种计算方法的计算结果对比（缆绳拉力极值）。

表2 多种计算方法的计算结果对比（缆绳拉力极值）

表2中，计算所用环境条件为MEG4 中的基准环境条件。OCIMF 计算方法中，缆绳受力采用等分法并乘以相应系数得到，详细可参考MEG 提供的算法示例。

4 结 语

本文通过对码头系泊系统的分析和合理简化，建立算法和用户界面，完成了一套简单易用、快速且准确的系泊分析软件的开发。本软件的使用可以达到以下目的：

（1）软件较低的使用门槛可以适用于更多的场景和用户；

（2）计算的简便、快速性能够让用户对于系泊优化从被动转变为主动；

（3）软件的目的是建立数据间的关系，系泊系统只是船舶系统的一部分，计算的即时性让用户能够直观看到“设计”与“结果”的数据关联，保证船舶设计的连续性和可靠性；

（4）自主可控的软件有非常好的扩展性，可以直接嵌入到船舶设计大系统中，实现更大范围的系统优化。

在本文软件开发的基础上，下一步将在软件中集成更多系泊设计的知识和经验，逐步实现从“被动”给出计算结果到“主动”提供设计优化建议的改变。