基于零模行波波速量化的高压输电线路双端故障定位方法

王 炜，王全金，尹 力，孙海霞，王 华，侯添钰，梁 睿

（1. 国网江苏电力有限公司连云港供电分公司，江苏 连云港 222004；2. 中国矿业大学 电气与动力工程学院，江苏 徐州 221116）

0 引言

高压输电线路故障会严重影响电力系统的安全稳定运行，其中80%以上的故障为单相、两相接地故障。为了保证及时、准确地定位和清除故障，实际高压输电线路故障定位一般以双端法为主、单端法为辅［1］。双端行波故障定位需要精确的波速，尤其在传输距离长的高压输电线路，行波波头的衰减较配电网线路更加显著，且微小的波速误差就可能导致较大的故障定位误差［2］。

实际线路中，行波波速会随着传播过程衰减，这一过程与线路参数以及行波的频率成分有关［3］。目前大部分行波故障定位方法（例如文献［4］所提方法）通常假设波速是接近光速的恒定数值，这一假设所带来的误差在短距离线路的场景下是可以忽略的，但是在高压输电线路场景下，由于高压输电线路的传输距离较长，波速在传输过程中会发生衰减，这使得行波的初始波速和到达首末端量测装置时的波速出现了明显的差异，此时继续将波速视为恒定值会导致较大的故障定位误差，给故障定位和清除工作带来巨大的困扰。部分学者针对如何消除行波波速的影响开展了研究，并提出了解决方法，但这些方法大多是从定位公式出发，通过公式变换从数学计算层面上消除波速变量（例如文献［5-7］所提方法），没有从根本上考虑波速衰减特性的影响，虽然考虑到了波速不恒定因素，但是依然以波速在传输路径上恒定为前提条件进行计算。进而有学者对行波波速在传输过程中的衰减特性进行了研究，并提出了考虑波速衰减的方法，但是这些方法大多有一定的局限性，例如：文献［8］研究了零模行波波速随故障距离的变化规律，给出了零模行波波速与故障距离的关系式，并以此进行故障定位，但是该方法在求解波速时，因为故障距离不可知，需要进行迭代运算；文献［9］利用故障距离与行波频率的关系以及行波频率与零模波速度的关系构造迭代公式提取零模波速，虽然可以得到较为精确的故障测距结果，但该方法依然需要迭代运算来求解波速，计算量较大。

为了消除行波波速对高压输电线路单相、两相接地故障定位的影响，本文对500 kV 高压输电线路的解耦和行波传播特性进行讨论，研究行波波速衰减规律，量化零模行波传输时间差与零模行波波速的关系；考虑故障点两侧波速差异，提出基于零模行波波速量化的高压输电线路故障精确定位方法。利用PSCAD／EMTDC 对所提方法进行仿真验证，结果表明该方法能够有效提升行波故障定位精度，且不易受过渡电阻的影响。

1 故障行波的传播特性分析

对于传统单回线路，采用卡伦鲍厄相模变换即可提取线路的零模信号，然而随着电力系统的飞速发展，同杆双回输电线路以其走廊资源占用少、传输效率高等优势，已广泛应用于我国500 kV 及以上电压等级高压电力系统中。高压输电线路在双回输电线路情况下的电磁耦合作用更为明显，单回输电线路的解耦方法不再适用［10-11］。为了对双回输电线路进行故障分析，需要对双回输电线路进行解耦。

并列运行的同杆双回输电线路结构如图1 所示，在分析过程中假设线路参数对称［12-13］，每回线的自阻抗为Zs。图中：Zm为相间互阻抗；Z'm为线间互阻抗；UM、UN分别为线路首、末端电源电压。

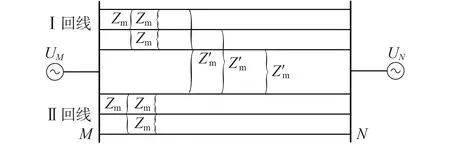
图1 同杆双回输电线路模型Fig.1 Model of double circuit transmission line on same tower

对双回输电线路间的电气量进行解耦后，使用卡伦鲍厄相模变换矩阵进行相模变换，从而得到解耦电气时域量进行故障分析。将线间、相间解耦结合得到的类卡伦鲍厄相模变换矩阵为［14］：

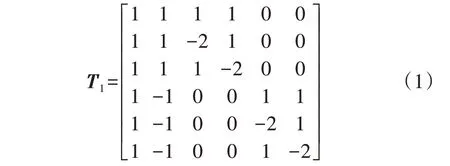
利用矩阵T1对同杆双回输电线路的电气量进行相模变换，从而得到解耦的模量进行故障分析。

线路发生故障后，故障行波在线路上以暂态过程的形式传播。根据导线的电感、电阻、对地电容和电导沿线的分布，可将线路看作是若干个π 形链组成的电路。在某一特定频率下，模量行波波速的表达式为［15］：

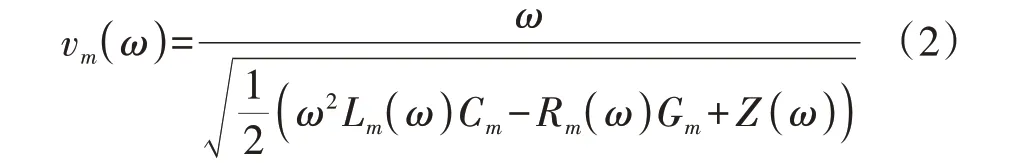
式中：m=0 表示零模行波，m=1 和m=2 表示线模行波；Rm(ω)与Lm(ω)分别为当角频率为ω时的线路电阻与电感；Gm和Cm分别为线路对地电导和线路对地电容，频率对这2 个参数的影响可以忽略不计，因此将其视为常数。由式（2）可以看出，行波波速与频率及线路参数有着紧密的联系，不同频率对应的零模和线模行波的波速也不相同［16-17］，即零模和线模行波的波速都会受到频率的影响而非恒定值。

故障行波信号中含有不同频率的信号，行波波头的幅值可以看作各频率分量波头幅值的叠加求和［17］，即：

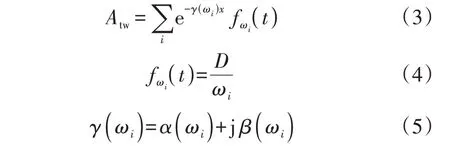
式中：x为行波的传输距离；ωi为行波波头频率分量i对应的角频率；Atw为行波波头幅值；γ(ωi)为频率分量i对应的特征算子；D为阶跃信号的幅值，由故障点过渡电阻、系统电压和线路参数决定；α(ωi)、β(ωi)分别为衰减系数和相位系数，表征零模行波在频率分量i下的衰减速度和相位速度，两者均随着频率的升高而增大。由式（3）—（5）可知，随着传播距离的增加，行波信号中各频率分量幅值的衰减程度不同，频率越高的分量，幅值衰减得越严重。由于零模行波和线模行波有着不同的传输路径，两者的信号衰减情况不一：零模行波经大地传播形成回路，线模行波经相与相之间传播形成回路，且大地阻抗大于线路阻抗，所以零模行波的衰减更为明显。

当行波波头到达首末端检测装置时，由于频率越高的分量速度越快，衰减也越快，波头中高频频段信号首先到达，幅值衰减严重，行波最前端的最高频信号由于幅值低于波头检测装置的阈值，无法触发波头检测装置，所以触发首末端波头检测装置的频率成分为传输速度稍慢的次高频行波分量的叠加。不同故障位置产生的行波有不同的传输时间，由于衰减特性，首末端检测到的频谱也不同，对应的波速便不同，这就导致首末端实际采集得到的行波波速是呈现衰减趋势的。

2 高压输电线路零模行波波速量化

零模行波由于在传输过程中首波头幅值衰减较快，波速随频率的变化也更明显，因此量化零模行波波速的变化，进而应用到行波故障定位方法中，可以有效提高故障定位的精确度。

为获取高压输电线路中故障零模电压行波的传播特性，基于实际高压架空输电线路参数，在仿真平台PSCAD／EMTDC中搭建500 kV同杆双回输电线路依频特性模型，如图2所示。线路型号为LGJ-300／40，线路长度为300 km。在距离线路首端150 km 处设置单相接地故障，采样频率为1 MHz，故障发生时刻为0.08 s，过渡电阻为50 Ω，在故障点后每隔15 km设置1 个行波信号测量点采集六相电压，共设置10个测量点M1—M10。

图2 同杆双回输电线路行波仿真模型Fig.2 Traveling wave simulation model of double circuit transmission line on same tower

故障发生后，对不同位置的测量点采集的电压信号进行解耦得到零模电压初始行波波形，见附录A 图A1。可以发现，由于行波高频分量衰减较快，初始行波波形越来越光滑，符合前文的分析。

双端行波故障定位方法主要是利用行波首波头到达线路首末端的时刻进行故障测距，线路的故障位置不同，行波首波头到达线路两端的时间也不同。以图2 为例，设M为首端，N为末端，首、末端A、B处配备量测设备，假设波头到达首端时刻为t1，到达线路末端时刻为t2，定义首末端传输时间差Δt=t1-t2。

当故障发生在测量点M1时，其距离线路首端更近，则故障行波将更快到达首端，此时有t1t2，Δt＜0；当故障发生在测量点M9时，其距离线路末端更近，则故障行波将更快到达末端，此时有t1>t2，Δt>0。以上分析表明，故障位置距离首端越远，Δt越大。可见，对于同一条线路而言，不同的Δt对应不同的故障位置。此外，故障位置与波速具有一定关系，可以通过拟合的方法提取该关系用于故障定位［10］。则利用传输时间差、故障位置、行波波速这三者之间的一一对应关系，使用可以直接测量获得的Δt代替未知的故障位置，建立Δt与行波波速的关系进行波速提取，可以避免因故障距离未知而引入迭代运算。

基于图2 所示的仿真模型，以5 km 为间隔依次设置故障点，采样频率设置为1 MHz。采用db6小波变换提取第1 层小波细节系数，即行波中频段为250～500 kHz的波形信息，在此频段上零模行波波速变化较大，变化趋势更明显［8］。利用小波模极大值方法识别首末端行波波头计算波速。在PSCAD 中通过仿真分析零模行波波速v0与首末端传输时间差Δt的变化关系，结果如图3所示。

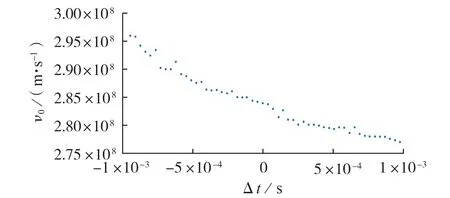
图3 v0随Δt的变化趋势的仿真结果Fig.3 Simulative results of changing trend of v0 along with Δt

由图3 可见，故障发生后，v0随Δt的增加呈单调减小的趋势。为精确刻画v0随Δt变化的函数关系，在MATLAB 中使用最小二乘法对仿真得到的散点图进行拟合，为保证拟合效果，选取指数函数、一次函数、二次函数以及三次函数进行拟合，拟合曲线见附录A图A2，对应的拟合结果见附录A表A1。

考虑到计算的复杂度以及拟合结果的可靠性，选用式（6）所示的三次函数拟合来描述v0随Δt变化的量化函数关系。

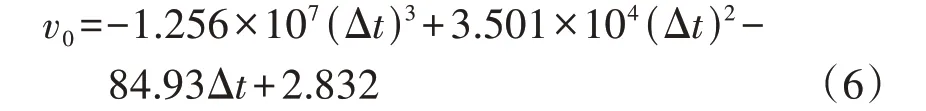
需要注意的是，当线路发生故障时，Δt越大意味着故障位置距离线路首端越远，相应地在图A2中对应的v0越小，因此首、末端分别检测到的行波波头由于具有不同的传输路径和传输距离，其波速衰减程度并不一致，需要各自进行波速的确定。

当故障发生时，定义ΔtAB、ΔtBA分别表示以首、末端为基准的故障零模初始行波波头到达线路两端测量点所需的时间差，且ΔtAB=-ΔtBA。图4 为v0随传输时间差变化的关系曲线，图中vA、vB分别为传输时间差ΔtAB、ΔtBA对应的首、末端零模行波波速，具体如式（7）所示。

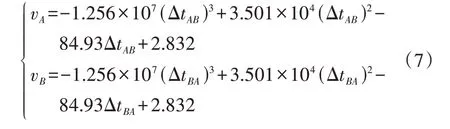
图4 零模行波波速随传输时间差的变化关系曲线Fig.4 Curve of zero-mode traveling wave velocity vs. transmission time difference

3 基于零模行波波速量化的双端故障定位方法

依据上述零模行波波速量化关系和故障点两侧波速选取方法，本文提出基于零模行波波速量化的双端故障定位方法，即在输电线路首、末端的点A、B处装设行波测量装置，当输电线路上发生故障（如附录A 图A3所示）时，故障行波沿输电线路传播，提取线路原始电压信号，然后通过相模变换获得零模电压行波信号，进一步通过小波变换提取零模行波首波头到达首、末两端的时刻tA、tB。

传统双端行波故障定位方法的故障距离计算公式为：

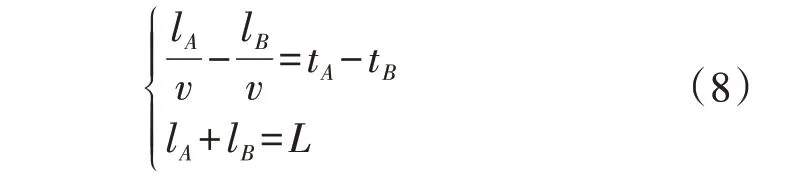
式中：L为输电线路的长度；lA、lB分别为故障点到首、末端测量点A、B的距离；v为选取的行波波速。可以看出，波速是影响双端行波故障定位方法精度的重要因素之一。为了提高输电线路故障定位的精度，基于式（8）所示的故障定位公式，采用通过量化关系获取的波头到两端测量点的不同波速进行故障位置的求解。因此，将式（8）改写为：

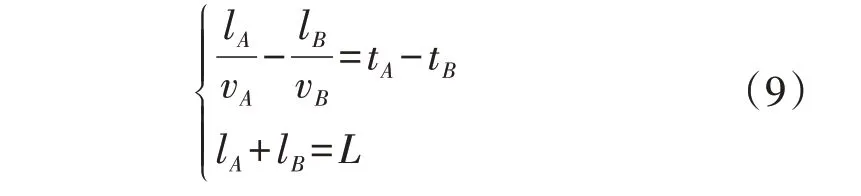
若令零模行波传输时间差ΔtAB=tA-tB，则可将式（9）改写为：

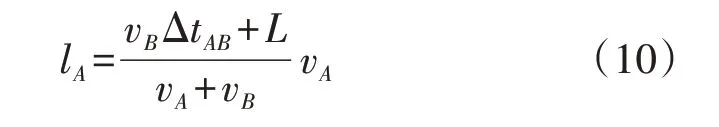
故障发生后，计算得到相应传输时间差，根据拟合得到的零模行波波速与传输时间差之间的函数曲线，求取对应的首、末端零模行波波速，然后将其代入式（10）即可进行故障定位。

综上所述，基于零模行波波速量化的双端故障定位的具体步骤如下：

1）根据实际线路参数搭建输电线路模型，离线拟合零模行波波速与传输时间差的函数曲线；

2）故障发生后，分别提取线路首端测量点A、末端测量点B的原始电压信号，然后依据线路的架设方式采用不同方式对其进行解耦，获得零模电压行波信号；

3）利用小波变换提取零模行波首波头到达首、末两端的时刻tA、tB；

4）计算传输时间差ΔtAB、ΔtBA；

5）根据拟合曲线求取由故障点到达首、末两端测量点的波速vA、vB，将vA、vB代入式（10）求解故障位置。

需要注意的是，考虑到仿真与实际现场的差距，在实际应用时步骤1）可以利用现场试验数据代替仿真数据，以获取更为真实的数据，降低误差，具体实现为：现场试验时，获取两侧波头到达时间差Δt，并计算两侧波速vA、vB，将仿真获得的数据替换为现场试验数据进行拟合，从而获得更真实的零模行波波速随传输时间差变化的关系曲线，其他步骤保持不变。

4 仿真验证

为了验证本文所提基于零模行波波速量化的双端故障定位方法，以某市电网500 kV RS 5237／5238线（同杆双回输电线路）为例，在PSCAD／EMTDC中搭建输电线路分布参数模型，线路长度为105.4354 km。设置距离线路首端37 km 处发生单相接地故障，故障发生时刻为80 ms，过渡电阻为50 Ω，仿真得到的首末端电压信号经过小波变换后提取的零模电压波形见附录A图A4。

分别利用小波模极大值的方法获取首、末端波头到达时间，计算得到相应的首末端传输时间差，将数据代入零模行波波速随传输时间差的变化关系曲线，得到vA、vB，将vA、vB代入式（10）求得故障发生在距离首端37.033 6 km 处，采用式（11）计算得到相对定位误差为0.03%。

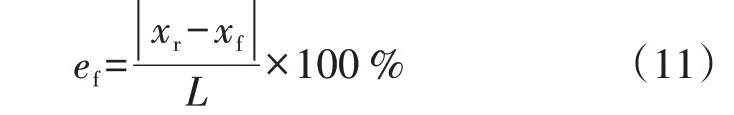
式中：ef为相对定位误差；xr为实际故障位置与首端的距离；xf为故障定位结果。

在线路不同位置处设置常见的单相接地故障、两相接地故障进行仿真，过渡电阻设置为50 Ω，仿真结果如表1 所示。由表可见，在线路不同位置发生单相、两相接地故障时，本文所提方法都有较高的故障定位精度。

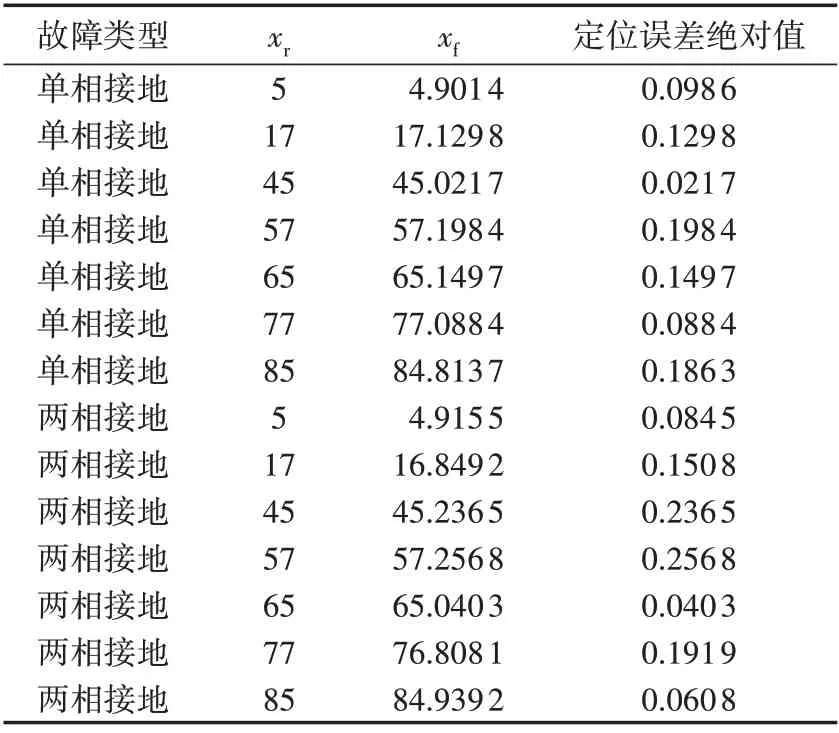
表1 不同故障位置下所提方法的故障定位结果Table 1 Fault location results of proposed method under different fault locations单位：km

为了验证本文所提方法在故障定位精确度方面的优势，将传统双端行波故障定位方法［18］（记为方法1）与本文方法进行对比，其中方法1 的线模行波波速取为经验值2.96×108m／s。在线路不同位置处设置过渡电阻为50 Ω 的单相接地故障，故障发生时刻为0.08 s，仿真时间为0.12 s，故障持续到仿真结束，方法1和本文方法的故障定位结果如表2所示。

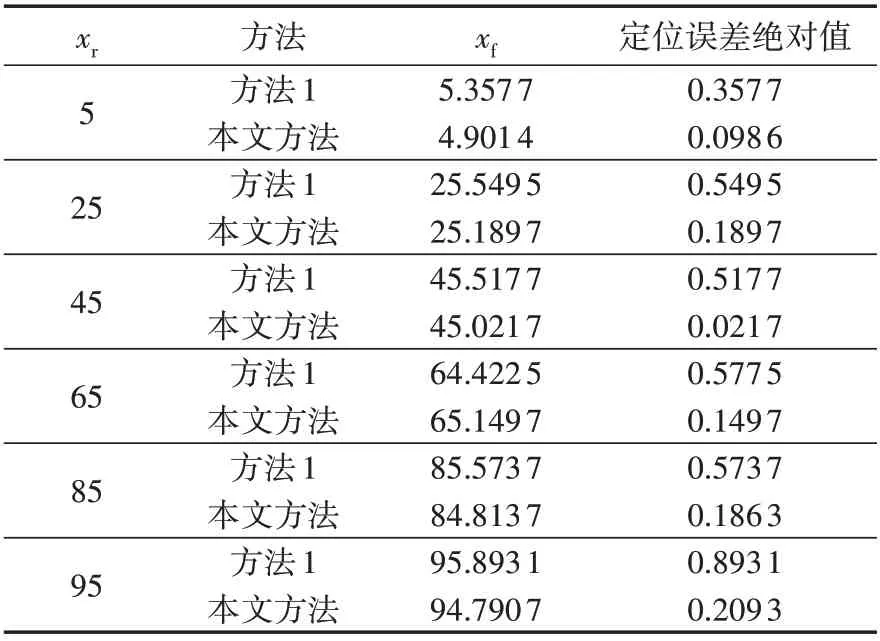
表2 不同方法的故障定位结果比较Table 2 Comparison of fault location results between different methods单位：km

由表2 可知，当输电线路的不同位置发生单相接地故障后，本文所提方法的故障定位误差绝对值均在0.3 km 以内，精度高于传统双端行波故障定位方法。

发生单相接地故障时，过渡电阻的大小也会影响故障定位的准确度。为了验证过渡电阻对本文所提方法的影响，在靠近线路首端和靠近线路末端处分别设置过渡电阻为100、200、500 Ω 的A 相接地故障，对应的仿真结果如表3所示。

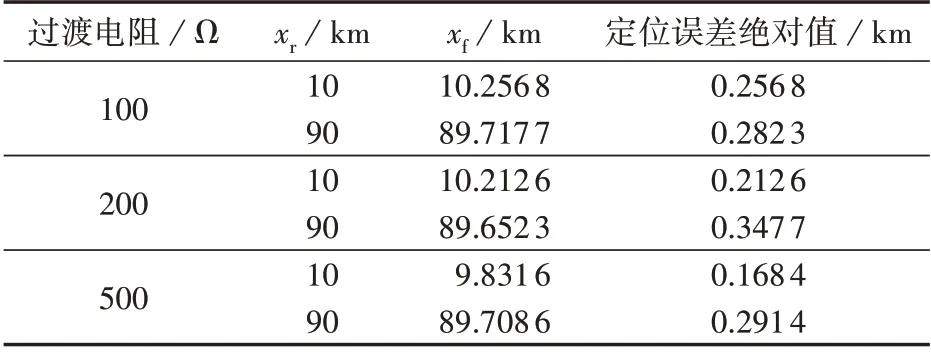
表3 不同过渡电阻下所提方法的故障定位结果Table 3 Fault location results of proposed method under different transition resistances

由表3 所示的仿真结果可知，当输电线路不同位置发生单相接地故障后，在过渡电阻为100、200、500 Ω 的情况下，本文所提方法的故障定位精度都较高，定位误差绝对值控制在了500 m 以内。因此本文所提方法对高压输电线路上不同过渡电阻的单相接地故障均有一定的定位精度。

为验证本文所提方法在不同线路长度下的有效性，分别将线路长度设置为100、150、200 km，在线路不同位置设置过渡电阻为100 Ω 的单相接地故障，得到仿真结果如表4所示。

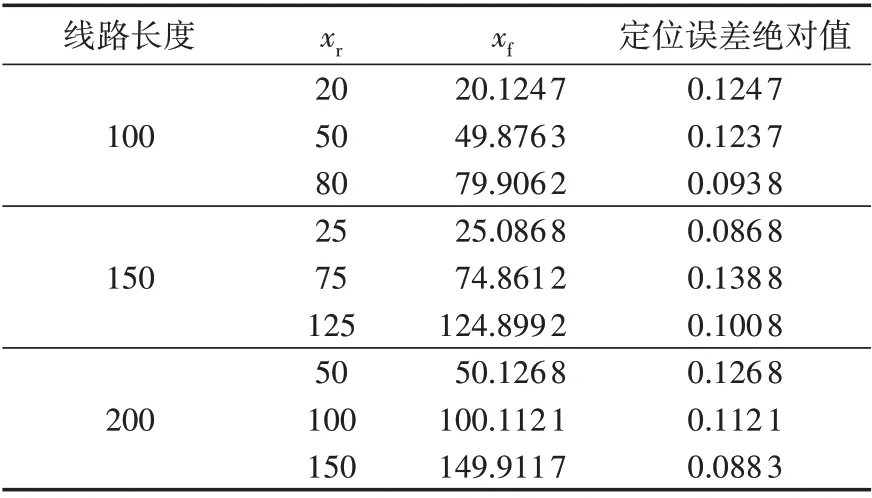
表4 不同线路长度下所提方法的故障定位结果Table 4 Fault location results of proposed method under different line lengths单位：km

由表4 可见，在不同线路长度下，本文所提方法都适用且能保证一定的故障定位精度。

5 结论

本文分析了行波不同频率分量之间传输速度以及幅值衰减的差异，得到输电线路行波波速变化趋势，并提出了基于零模行波波速量化的高压输电线路双端故障定位方法，主要结论如下：

1）行波波速会随着传输过程衰减，当故障发生时，由于故障点两侧故障距离以及行波传输路径的不同会导致两侧的平均波速存在差异；

2）通过三次函数拟合的方法量化了传输时间差与零模行波波速的关系，得到传输时间差与波速的函数曲线，并提出了故障点两侧的波速选取方法；

3）基于故障点两侧行波波速差异和零模行波波速量化关系提出改进的故障定位算法，和现有方法相比，所提方法能够有效减小波速对单相、两相接地故障定位的影响，显著提升了故障定位精度。

附录见本刊网络版（http：//www.epae.cn）。