大扰动后正阻尼单机水电系统频率振荡的近似及适应性分析

王嘉伟，熊鸿韬，刘晓博，杨 滢，张建承，庄文彬，华 文，薛安成

（1. 华北电力大学 新能源电力系统国家重点实验室，北京 102206；2. 国网浙江省电力有限公司电力科学研究院，浙江 杭州 310014；3. 国网浙江省电力有限公司调度控制中心，浙江 杭州 310007）

0 引言

近年来，国内外高水电占比电网在实际运行或试验中，出现了多次复杂的超低频频率振荡事故，威胁着电网的安全稳定运行［1⁃3］。例如，云南电网在试验中，出现了系统负阻尼效应导致的频率振荡失稳问题，以及调速器增强型死区导致系统不存在平衡点，其引起频率在死区附近振荡的问题［4］。另一方面，某大电网仿真表明，在线路N-2 故障下，当故障持续时间为40 ms 时，系统会恢复稳定（系统正阻尼），而当故障持续时间为80 ms 时，系统会发生持续的调速器限幅参与的超低频频率振荡（大扰动后正阻尼的振荡）［5］。目前，超低频频率振荡的数学机理可分为负阻尼振荡、光滑的强迫振荡和切换型振荡［6］。

在负阻尼振荡方面，文献［7⁃8］分析指出，水电机组调速器提供负阻尼导致一次调频过程中小扰动失稳，是造成实际电网超低频频率振荡的直接原因之一。在对应的分析方法上，目前较为常用的是基于时域的状态空间模型的特征根分析法以及基于频域的复转矩系数法。强迫振荡易出现在本身阻尼较弱而外界扰动较大的系统中［9］。文献［10-11］利用端口供给能量法，分析可得超低频频率振荡起振阶段的诱发原因为负阻尼；并利用模态图和快速傅里叶分解法，分析认为持续振荡阶段的特征类似于强迫振荡的全局共振，即发电机之间同相位共振。上述负阻尼振荡和光滑的强迫振荡分别对应于系统负阻尼和弱阻尼时在小扰动后的光滑振荡，其对应于光滑的动力系统，相应的分析方法大多是基于小扰动后电力系统的线性化模型。值得注意的是，调速器中的死区和限幅非线性切换环节也会对振荡特性产生较大影响［4⁃5］。含死区和限幅的电力系统是非光滑动力系统，大扰动后死区和限幅参与的振荡是大范围（全局）的非光滑振荡（即切换型振荡），其相应的数学机理不同，传统光滑系统的小扰动分析方法可能不再适用。

在切换型振荡方面，目前发现了3 种不同类型的切换型超低频频率振荡：一是严重大扰动后具有稳定平衡点（局部正阻尼）的系统，在初始状态偏离平衡点较远时，无法返回平衡点的稳定域而进入非光滑极限环的吸引域时出现的切换型振荡［5，12-13］；二是在扰动后，具有不稳定平衡点（局部负阻尼）的系统轨线发散时，死区、限幅等环节参与形成的切换型振荡［14］；三是扰动后无平衡点的系统出现的死区参与的切换型振荡［4，13］。但是，上述研究仅通过仿真发现了切换型频率振荡这一现象，并定性分析了其随参数变化的非光滑分岔特性，缺少相应的量化分析手段。

考虑调速器死区时，文献［15-16］建立了含死区的分段线性系统模型，通过不同扰动下的解析求解［15］、描述函数［16］等方法，分析了调速器的不同死区类型对单机简化系统稳定性的影响，获得了水轮发电机组的死区影响频率振荡特性的一般规律。进一步，文献［17］定义了扩展描述函数，定量分析了多个死区环节对多机组合系统频率振荡的影响，并提出通过死区配置抑制超低频频率振荡的方法。值得注意的是，上述研究仅分析了单一死区切换环节参与的频率振荡，缺乏对多个不同类型切换环节参与的振荡分析（未同时考虑限幅）。此外，描述函数法是一种近似分析方法，使用时具有一定的假设前提［18］，文献［16-17］直接采用描述函数法，但均未涉及适应性分析。将非光滑系统近似为光滑系统，能否精确近似非光滑单机水电系统的超低频频率振荡，在其他文献中也未见分析报道。

鉴于此，本文在已有研究成果的基础上，针对大扰动后正阻尼的非光滑单机水电系统出现的死区和限幅参与的切换型频率振荡现象，应用分段的描述函数，说明了近似光滑系统的稳定极限环可近似大扰动后正阻尼的非光滑系统出现的切换型振荡。并分析了不同的限幅参数对振荡特性的影响以及描述函数法的适应性。

1 单机水电系统模型及其振荡现象

1.1 含非线性切换环节的系统模型

当电力系统发生超低频频率振荡时，所有机组频率基本保持同相位振荡，因此可以将系统简化为单机系统进行分析［19］。另一方面，文献［7⁃8］研究表明，超低频频率振荡主要与水电机组的一次调频过程不稳定相关。故针对频率振荡问题，本文分析的带负荷单水电机组简化系统（以下简称单机水电系统）忽略了励磁器，仅考虑调速器。

单机水电系统的调速器数学模型如附录A 图A1 所示，其包括调节系统、电液伺服系统、水轮机3个部分，各部分的传递函数分别为：

式中：KW为频率偏差放大倍数；KP、KI分别为比例、积分环节的放大倍数；bp为永态转差系数；KP1为电液转换模块的放大倍数；Ty为接力器时间常数；TW为水锤效应时间常数。进一步，发电机部分的传递函数如式（4）所示。

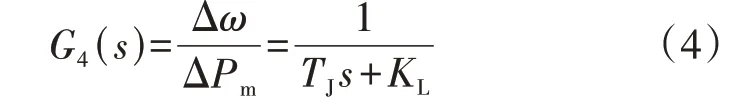
式中：Δω为角频率偏差；ΔPm为机械功率偏差；TJ、KL分别为发电机转动惯量和负荷的单位调节功率。综上，简化单机水电系统线性部分的开环传递函数可表示为：

图A1 中调速器含多个死区和限幅非线性切换环节，本文仅考虑一次调频死区和限幅环节F(x4)，其示意图如图1 所示。图中，切换环节的输入信号x4为角频率偏差的负值；±ε和±λ分别为死区值和限幅值。

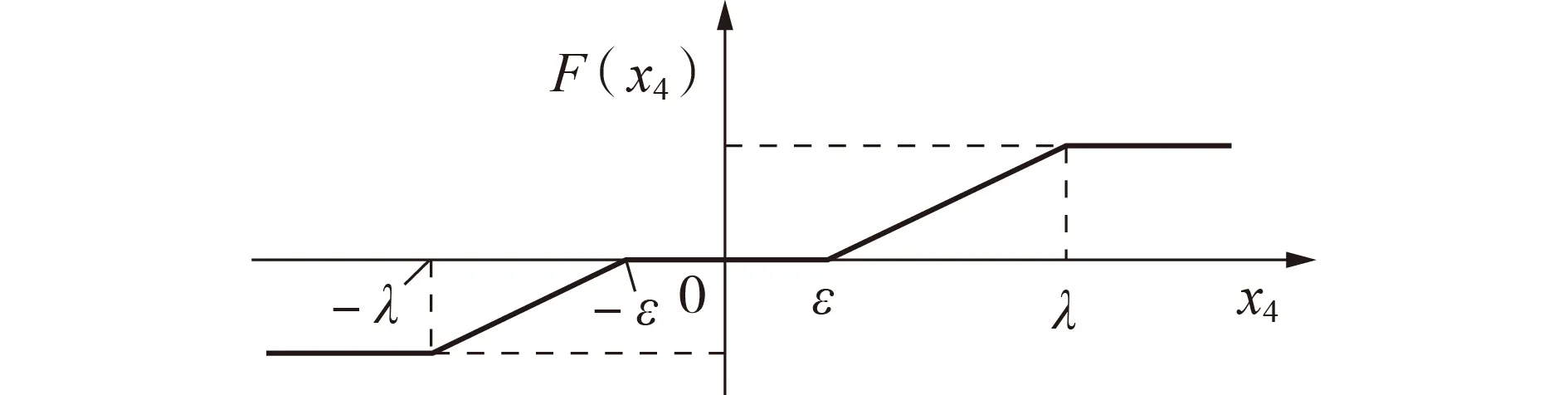
图1 死区和限幅切换环节Fig.1 Switching link of dead zone and limitation

1.2 大扰动后正阻尼系统的切换型频率振荡现象

对于上述单机水电系统，采用实际电网中引发超低频频率振荡事故的某一主要机组的典型参数取值为：角频率参考值ωref=1 p.u.，调速开度参考值Yref=1 p.u.，KW=1.1，KP=5，KI=1，KP1=40，bp=0.03，Ty=13.86 s，TJ=10 s，KL=1.5，TW=1.6 s，ε=0.000 8 p.u.，λ=0.0308 p.u.。

根据文献［12］，当负荷为额定参数，即PL=1 p.u.时，单机水电系统存在稳定的平衡点（局部正阻尼）。当大扰动造成系统初值（即系统的初始状态）在一定范围内波动（即初值偏离平衡点较远）时，系统将发生死区和限幅参与的切换型频率振荡。不同角频率偏差初值下，系统的角频率偏差变化如图2 所示，图中角频率偏差为标幺值。由图可知：当小扰动造成角频率偏差的初值为0.015 7 p.u.（实线）时，系统角频率经调速器的调节，最终角频率偏差为0，这说明频率振荡逐渐衰减，单机水电系统恢复稳定，对应着系统轨线最终收敛到稳定的平衡点；当大扰动造成角频率偏差的初值为0.015 8 p.u.（点划线）时，系统最终发生了死区和限幅参与的频率振荡，其振荡幅值为0.032 5 p.u.，振荡频率为0.1073 Hz。

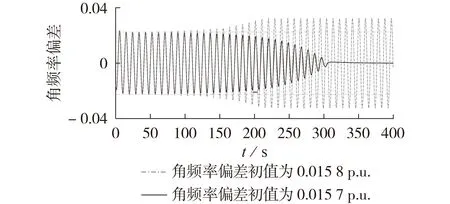
图2 角频率偏差的时域变化Fig.2 Time domain variation of angle-frequency deviation

2 描述函数法

2.1 总体介绍

在进行无外部输入信号非线性系统的稳定性分析时，描述函数法是一种计算非线性系统振荡参数的经典近似方法。假设系统发生振荡时，非线性部分的输入信号为正弦信号，即：

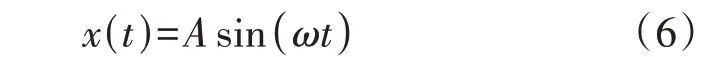
式中：A和ω分别为输入信号的振荡幅值和振荡角频率；t为时间。

在具有静态非线性特性的非线性环节中，当输入信号为正弦信号时，其输出信号是一个与输入信号周期相同的周期函数［18］。将输出信号y(t)用傅里叶级数展开，并忽略高阶项可得：

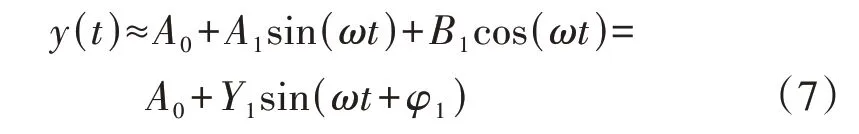
式中：A0为直流分量；A1、B1分别为输入信号基波正、余弦分量的幅值；Y1、φ1分别为输出信号基波分量的幅值和相位。则非线性部分的描述函数N(A)可表示为输出信号的基波分量和输入信号的复数比，如式（8）所示。

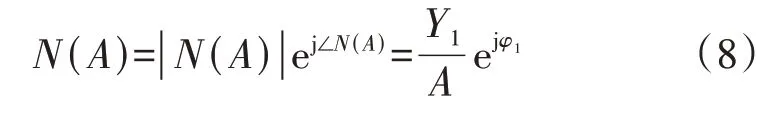
此时，整个非线性系统（非光滑系统）可以在频域内近似为一个单环负反馈控制系统（近似的光滑系统），如图3 所示，图中r、z分别为近似控制系统的输入、输出信号。描述函数法只考虑周期运动变量x、y、z的基波分量，不计高次谐波分量，此时要求系统的线性部分G0(jω)具有较好的低通滤波性能，即在能阻止高次谐波通过时，描述函数法有较高的精度。

图3 频域近似控制系统Fig.3 Approximate control system in frequency domain

2.2 应用准则

根据图3，频域近似控制系统的闭环频率特性为：

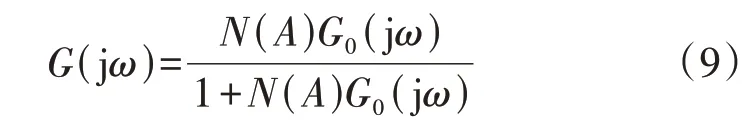
其特征方程为：

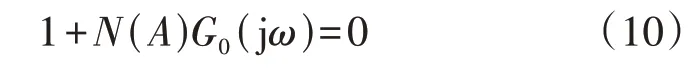
可变化为：

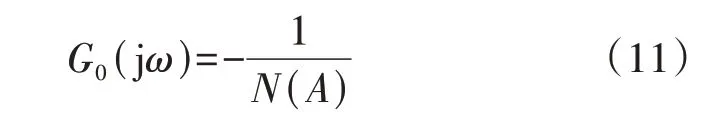
类似于Nyquist 判据的最常见形式［18］，可以通过图4 所示复平面上的G0(jω)曲线和-1/N(A)曲线的相对位置关系来分析频域近似控制系统的稳定性。图中：G0(jω)表示ω从0 增大到+∞的开环频率特性曲线；-1/N(A)表示输入信号幅值A从0 增大到+∞的负倒特性曲线。

图4 描述函数法的判别准则Fig.4 Discriminant criteria of describing function method

1）如果G0(jω)曲线始终包围／不包围-1/N(A)曲线，则表明近似系统不稳定／稳定。

2）如果G0(jω)曲线和-1/N(A)曲线存在交点，则表明近似系统中存在极限环，根据交点的不同，又需进一步区分。

（1）从不稳定区到稳定区的穿出交点（Acr1，ω1）（Acr1和ω1分别为该交点下对应振荡的幅值和角频率）对应的是稳定极限环。在穿出交点附近，若输入信号幅值A>Acr1，则系统运行点位于稳定区，振荡会逐渐衰减；若输入信号幅值AAcr1，则系统运行点位于不稳定区，振荡会进一步发散；两者最终都收敛到穿出交点处的稳定极限环。

（2）从稳定区到不稳定区的穿入交点（Acr2，ω2）（Acr2和ω2分别为该交点下对应振荡的幅值和角频率）对应的是不稳定极限环。穿入交点处的稳定性与输入信号幅值A有关，若振幅在稳定区，则系统振荡逐渐衰减，最终恢复稳定（收敛到稳定的平衡点）；若输入信号幅值在不稳定区，则系统振荡进一步发散，最终收敛到稳定的极限环。

（3）如果2 条曲线为相切关系，那么切点处对应的是半稳定极限环。

3 基于描述函数法的近似分析

3.1 描述函数法的分析结果

在固定参数下，对比基于描述函数法的近似分析结果与实际仿真结果，初步验证描述函数法用于近似分析大扰动后正阻尼的单机水电系统出现的死区和限幅起作用的切换型频率振荡的适用性。

对于图1 所示的死区和限幅切换环节，其输入输出信号为奇对称，故在图2 所示正弦输入信号下，经切换环节的输出信号傅里叶级数展开中，A0=0，B1=0。因此，切换环节的输出信号中不含直流分量，且其描述函数仅含实数部分。死区和限幅切换环节的输入输出信号具有分段特性，故其描述函数也需分段表示，如式（12）所示［18］。

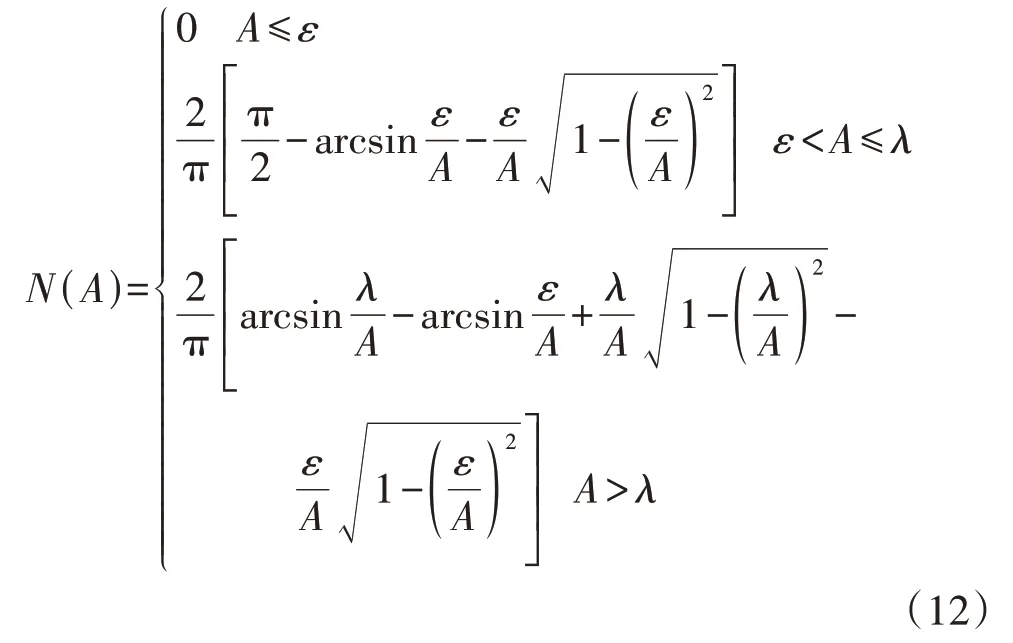
在1.2 节设置的系统参数下，由式（5）、（12），可得到开环频率特性曲线G0(jω)和负倒特性曲线-1/N(A)，在复平面上如图5所示，图中横纵轴刻度值均为标幺值。负倒特性曲线-1/N(A)也分为3段：当A≤0.000 8 时，-1/N(A)在负无穷远处；当0.000 8A≤0.030 8 时，-1/N(A)的第二段由图中圆圈构成；当A>0.0308时，-1/N(A)的第三段为图中直线。负倒特性曲线-1/N(A)与开环频率特性曲线G0(jω)有2 个交点：①圆圈所对应的交点为穿入交点，穿入交点处的振荡角频率为0.673 3 rad／s（0.107 2 Hz），振幅为0.022 6 p.u.，其对应的是不稳定极限环的幅值；②直线对应的穿出交点，穿出交点处的振荡角频率为0.673 3 rad／s（0.107 2 Hz），振幅为0.032 5 p.u.，其对应的是死区和限幅作用的稳定极限环（A>λ）。

图5 开环频率特性和负倒特性曲线Fig.5 Open-loop frequency characteristics and minus reciprocal curves

描述函数法的分析结果表明，本文分析的含死区和限幅切换环节的单机水电系统在稳定平衡点外，同时存在一个不稳定极限环和一个稳定极限环。因此，从系统动力学角度看，根据输入信号幅值的不同，系统表现出不同的稳定性。具体为：当扰动后输入信号幅值较小（小扰动后的输入信号幅值），输入信号幅值处于稳定平衡点的稳定域内部时，该振荡最终平息，恢复稳定（轨线收敛到稳定平衡点）；当扰动后输入信号幅值较大（大扰动后的输入信号幅值）时，输入信号幅值不在稳定平衡点的稳定域内部，而在稳定极限环的吸引域内部，此时，轨线收敛到稳定极限环，即近似控制系统发散形成稳定持续的振荡。

同时，该分析结果与1.2节仿真获得的振荡信息（振幅为0.032 5 p.u.，振荡频率为0.107 3 Hz）接近。因此，在本文参数设置情形下，基于描述函数法的频率振荡的近似精度较好，近似光滑系统的稳定振荡可近似为非光滑系统的大范围（死区和限幅起作用）切换型振荡。

3.2 限幅参数的影响分析

改变非光滑结构的限幅值，近似的描述函数法和仿真法求得的稳定极限环（切换型振荡）对应的振荡频率和振荡幅值对比如表1 所示，表中振荡幅值为标幺值，后同。由表1可得如下结论：

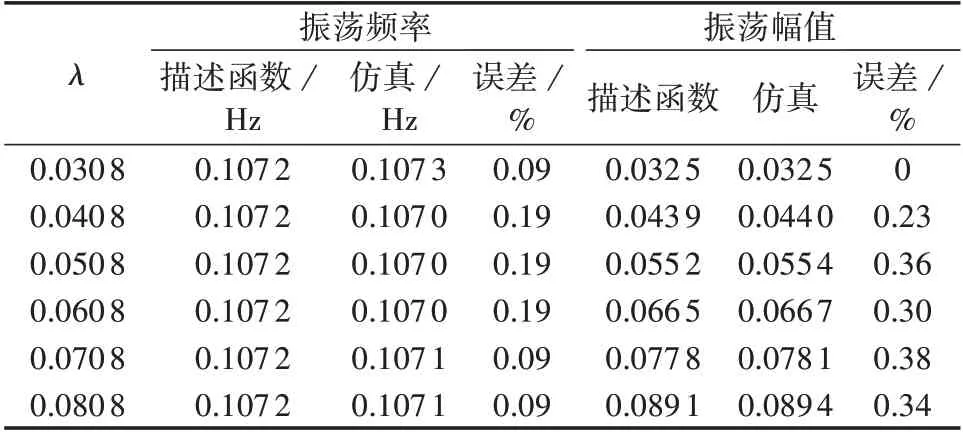
表1 不同限幅下的结果对比Table 1 Results comparison under different limitations

1）基于描述函数法的近似和仿真计算结果，在误差允许的范围内，基本一致；

2）限幅参数变化时，非光滑单机水电系统仿真中切换型频率振荡的振荡幅值变化，而振荡频率基本不变，该现象可通过图5 所示的开环频率特性和负倒特性曲线解释，即限幅参数变化时负倒特性曲线-1/N(A)仍在实轴上，但各处对应的输入信号幅值A发生变化，而开环频率特性曲线G0(jω)不随限幅变化而变化，故2 条曲线的交点对应的稳定极限环，其振荡角频率ω不变，而振荡幅值A变化。

4 描述函数法的适应性分析

本节进一步分析单机水电系统的线性部分的参数变化（线性部分的低通滤波性能变化）时，描述函数法的适应性。与第3 节分析类似，改变一次调频比例积分PI（Proportional Integral）环节的比例增益参数KP，描述函数法和仿真法求得的稳定极限环（切换型振荡）对应的振荡频率和振荡幅值对比如表2 所示，可得如下结论。

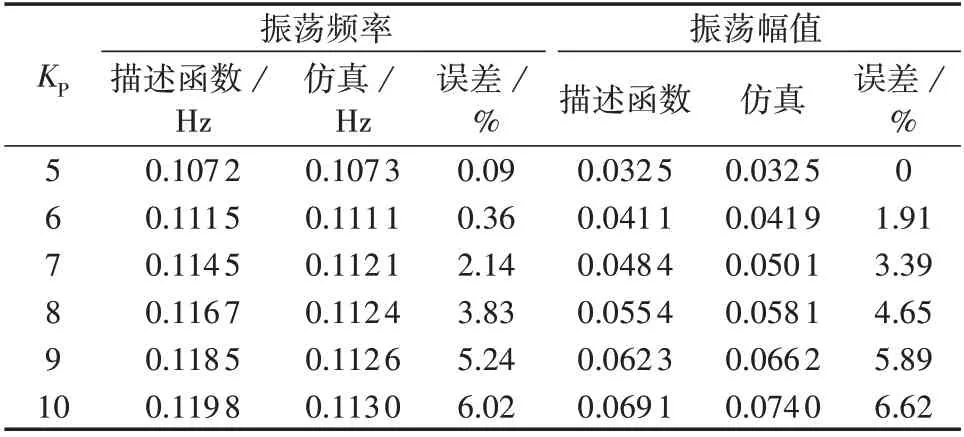
表2 不同KP下的结果对比Table 2 Results comparison under different values of KP

1）当KP变化时，非光滑单机水电系统仿真中切换型频率振荡的振荡频率和幅值均会变化。这是因为当KP变化时，由图5 可知，开环频率特性曲线G0(jω)变化，其与负倒特性曲线-1/N(A)之间的穿出交点（稳定极限环）所对应的振荡频率和振荡幅值均发生变化。

2）对比描述函数法和仿真计算的结果，在KP较小时，二者的振荡频率和幅值基本一致；在KP较大时，振荡频率和幅值误差偏大。表明描述函数法成立的前提可能受到挑战，即系统不具有低通滤波性质。

由于本文分析的切换环节和输入信号均为奇对称，输出信号中主要含有奇次谐波。线性部分G0(jω)的基波项和3 次谐波项的幅值增益的计算结果如表3所示。

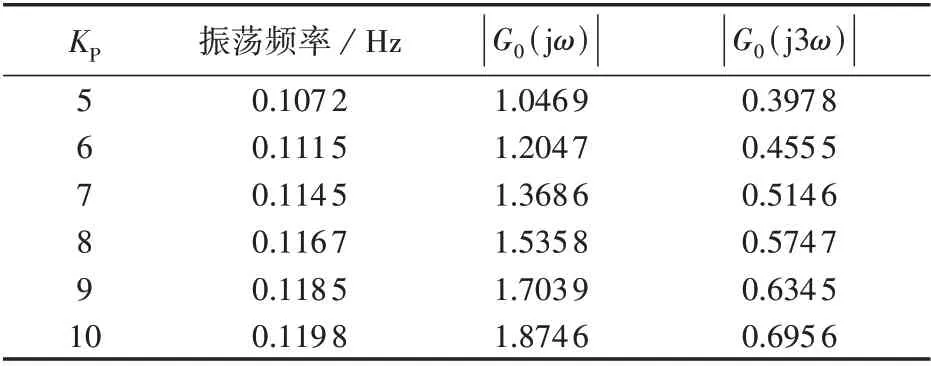
表3 不同KP下的幅值增益Table 3 Amplitude gain under different values of KP

由表2、3 可知：当KP较小时，线性部分的3 次谐波项的幅值增益较小，这说明线性部分的频率特性G0(jω)对高次谐波分量的抑制效果较好，因此，使用描述函数法的分析结果与仿真法基本一致，精度较高；当KP较大时，3 次谐波项的幅值增益变大，这说明线性部分的频率特性G0(jω)对高次谐波分量的抑制效果变差，因此，分析结果的误差也增大。同理可得，当单机水电系统线性部分的积分参数KI和水锤效应时间常数TW变化时，描述函数法的近似分析结果与仿真结果之间的误差也会随3 次谐波幅值的增大而增大，如附录A的图A2、A3所示。

上述分析表明，描述函数法在非光滑系统的分析中仅考虑了基波分量，为近似方法。如果线性部分对高次谐波的滤波性能变差（即3 次谐波项的幅值增益变大），那么基于描述函数法的分析结果与实际情况的差异也将变大。因此，在使用描述函数法时，尤其需要注意系统对高次谐波的滤波性能。

5 结论

针对大扰动后正阻尼的非光滑单机水电系统出现的死区和限幅参与的切换型频率振荡，提供一种基于分段描述函数的近似分析方法，得到主要结论如下。

1）在小扰动后正阻尼的单机水电系统，经调速器调节，系统频率恢复稳定；在大扰动后正阻尼的单机水电系统，会出现死区和限幅参与的切换型频率振荡现象。

2）当参数满足低通滤波条件时，基于描述函数法分析的光滑系统的稳定极限环，可近似对应大扰动后正阻尼的非光滑系统出现的死区和限幅起作用的切换型振荡；且可解释不同限幅参数下切换型频率振荡的振荡幅值变化而振荡频率基本不变的现象。

3）参数变化可能导致单机水电系统在振荡频率附近的滤波性能变差，3 次谐波无法忽略，导致采用描述函数法的近似分析结果的精度也变差。

本文方法主要用于单机水电系统。对于高维的含有不同死区和限幅的实际多机水电系统，在不同扰动下如何确认哪些机组哪些死区和限幅参与振荡，并结合死区和限幅组合分析，还需要进一步研究。

附录见本刊网络版（http：//www.epae.cn）。