适用于次同步振荡分析的直驱式风电场等值方法

袁赛军，郝治国，舒 进

（1. 国网湖南省电力有限公司电力调度控制中心，湖南 长沙 410004；2. 西安交通大学 电气工程学院，陕西 西安 710049；3. 西安热工院有限公司，陕西 西安 710054）

0 引言

随着大规模、高比例、远距离输送的直驱风机PMSG（Permanent Magnet Synchronous Generator）并网，现代电力系统在运行中出现了新型次同步振荡SSO（Sub-Synchronous Oscillation）现象。区别于传统的火电机组和双馈式风电机组，2015 年7 月1 日在我国新疆哈密地区发生的大规模直驱风机次同步振荡事故与机组轴系和输电线路串联补偿均无关，且振荡电流以超同步频率分量为主，因而适用于传统火电机组和双馈式风电机组的次同步振荡相关机理及抑制措施难以指导直驱风机的并网运行［1⁃2］。

阻抗分析法作为近年来兴起的、为国内外学者重点关注的次同步振荡分析方法，被广泛应用于分析直驱风机与弱交流电网之间的相互作用问题［3⁃6］。阻抗分析法的核心原理在于：基于谐波线性化理论，分别建立直驱风机侧和电网侧的小信号线性化阻抗解析模型，然后利用奈奎斯特判据对系统稳定性进行判定［7⁃8］。目前基于阻抗分析法的直驱风机并网次同步振荡相关研究取得了较为一致的结论：从风机侧来看，直驱风机锁相环PLL（Phase-Locked Loop）参数的选取是引发系统次同步振荡的主要影响因素［3⁃5］；从电网侧来看，当电网阻抗增大、电网短路比SCR（Short Circuit Ratio）减小时，直驱风机接入弱交流电网易引发系统次同步振荡，称这一场景为直驱风机并网引发次同步振荡的典型场景。

然而，现阶段研究对象普遍为单台直驱风机，对于整座直驱式风电场和电网的相互作用机理仍然缺乏完整严密的数学分析，其原因在于大型风电场阻抗建模和仿真分析均面临“维数灾”的问题。研究适用于次同步振荡分析的风电场等值方法是实现由单机并网分析到风电场并网分析的必经之路，其包含降阶、适用2 个基本要求。由阻抗分析法的核心原理可知，适用于次同步振荡分析的风电场等值方法评价标准在于降阶模型对原风电场外阻抗特性的逼近程度。同时，为了仿真分析的需要，降阶后的模型最好具有结构保持特征，能够降阶为几台风机的数学模型，而非单台风机的数学表达式。

现有分析风电场与交流电网之间的相互作用的研究思路大致分为如下3 种：①建立详细模型，即对每台风机进行单独建模，相关学者在应用阻抗分析法研究直驱式风电场并网次／超同步振荡相互作用机理时，提出了风电场阻抗聚合方法［9⁃10］，但是聚合阻抗模型阶数随风机台数成比例增加，甚至超过仿真平台节点数限制；②从风机数学模型出发，获得单机降阶模型［11⁃14］，但其缺点在于所得降阶数学模型不再具有风机的结构保持特征；③获得风电场的等值模型，即用1 台或多台等值机来模拟整座风电场［15⁃17］，然而现有等值方案仅从保持风电场电磁暂态特征出发，以风速等指标为分群特征，未拟合风电场外阻抗特性，因而无法适用于风机并网后的次同步振荡分析。

因此，以等值前、后风电场外阻抗特性相一致为目标，本文提出了一种直驱式风电场等值方案，将直驱式风电场等值降阶为具有结构保持特征的等值机，在分群聚合和等值降阶2 个步骤中量化了误差。分别以直驱式风电场含同型号直驱风机和不同型号直驱风机为例，对所提方案所得等值机（群）的阻抗特性仿真结果和原始风电场外阻抗特性扫频结果进行对比。结果表明所提方案等值模型与直驱式风电场原始阻抗模型具有较为接近的外阻抗特性，适用于直驱式风电场并网后的次同步振荡分析。

1 直驱式风电场拓扑及其阻抗模型

图1 为直驱式风电场并网系统的典型布局。每台直驱风机及变流器经箱式变压器（以下简称“箱变”）升压至35 kV后汇集至1条集电线路处，各条集电线路由中压母线汇集送出，将风电经直驱式风电场主变输送至电压等级为110 kV 或220 kV 的高压电网中。

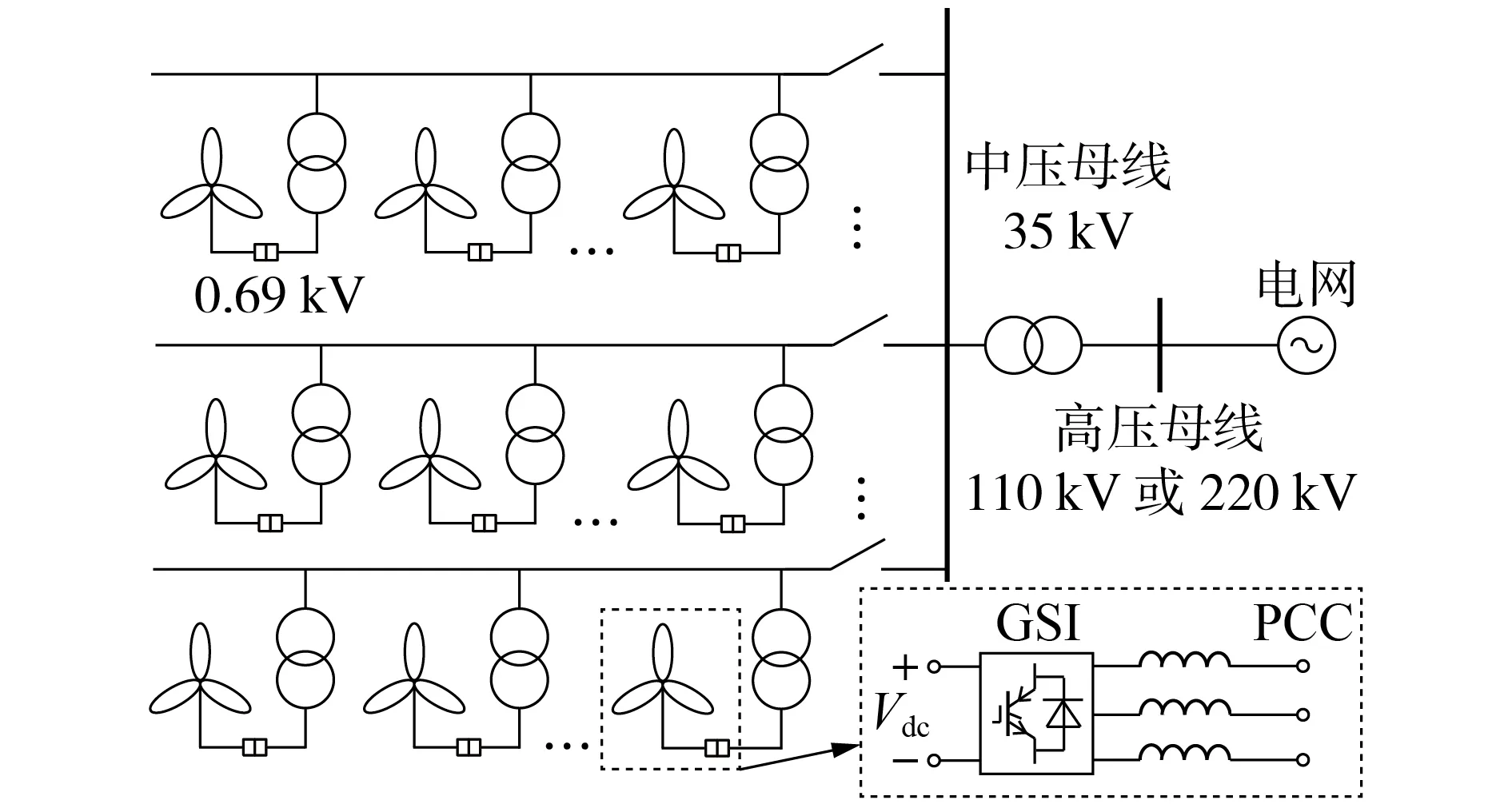
图1 直驱式风电场并网系统的典型布局Fig.1 Typical layout of grid-connected system with PMSG-based wind farm

在分析直驱式风电场并网次同步振荡时，往往将每台直驱风机及变流器简化为图1 虚线框内的电流源型逆变器经滤波电感并网的形式（GSI 为网侧逆变器；PCC为风机并网点；Vdc为逆变器直流母线电压）。定义单台直驱风机序阻抗为从箱变低压侧看进去的端口阻抗，其锁相环传递函数Tp(s)及正序端口阻抗Z(s)表达式分别为［4］：

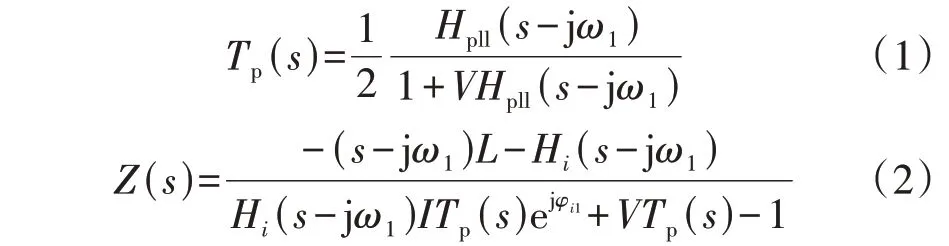
式中：ω1=2πf1为工频角频率，f1为工频；Hpll(s)=(kp+ki/s)/s，kp、ki分别为锁相环比例积分PI（Proportional Integral）调节器比例、积分参数；V为直驱风机机端正序电压幅值；L为变流器出口等效滤波电感；Hi(s)=kip+kii/s，kip、kii分别为电流内环PI 调节器比例、积分参数；I为直驱风机的输出电流；φi1为直驱风机输出电流的功率因数角。

从图1 中可以看出，由于大型直驱式风电场中集电线路的长度、参数各异，在进行直驱式风电场等值时，主要处理的是直驱风机阻抗与集电线路阻抗的串、并联关系。为探究集电线路阻抗对直驱风机机端电压的影响，根据附录A 表A1 所示的某实际直驱式风电场参数，选取一条汇集10 台直驱风机、长度为6.2 km 的集电线路，以100 MW 为基准，计算出工频下折算到35 kV侧的参数如下：集电线路阻抗Z35=0.073 4+j0.051 8 p.u.；箱变阻抗ZT=j0.325 p.u.；额定工况下直驱风机阻抗ZPMSG=-6.67 p.u.。

即使在集电线路汇集直驱风机台数多、直驱风机满发以及集电线路很长这3 种情况同时出现的工况下，直驱风机阻抗也远大于集电线路及箱变阻抗之和。因此，对于实际的直驱式风电场，可假设每台直驱风机机端电压等于直驱式风电场主变低压侧电压，即所有直驱风机之间为纯并联关系，可不计其间复杂的拓扑结构。在该条件下直驱式风电场的聚合阻抗ZΣ(s)的表达式为：

式中：Zk'(s)为第k'台直驱风机的正序端口阻抗；n'为直驱风机总数。

2 基于阻抗灵敏度分析的分群聚合

2.1 阻抗灵敏度分析

分群聚合是直驱式风电场等值的第一步，首先应该衡量不同直驱风机参数对并联阻抗模型阶数的影响，其次应该按照影响程度对不同直驱风机参数进行排序。考虑到式（2）所示的幅频特性和相频特性完全对称于50 Hz，令s'=s-jω1，进行位移变换后展开，忽略s'上标可得：

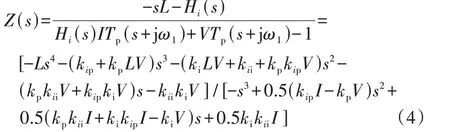
从式（4）可以看出，直驱风机输出电流I只出现在分母，风速与I存在相关关系，因此在计算直驱式风电场并联阻抗时，单纯因风速的差异不会增加直驱式风电场聚合阻抗的阶数。因此，与输出电流相关的风速不应该成为直驱风机分群指标；而锁相环参数kp、ki和电流内环参数kip、kii以及等效滤波电感L将成为直驱风机分群指标，进而影响直驱式风电场聚合阻抗的复杂度。故针对上述5 个参数进行阻抗灵敏度分析，以确定直驱风机分群指标。直驱风机正序端口阻抗Z相对于参数x（kp、ki、kip、kii、L）的归一化灵敏度表达式见式（5）。

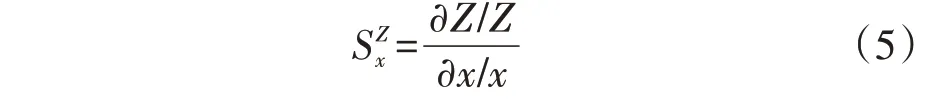
设V=636 V；I=1 847 A；电流内环控制参数kip=0.25，kii=355；锁相环控制参数kp=0.085，ki=32；L=0.15 mH。将上述参数代入式（5），即可计算SZx。根据文献［4］得出的直驱风机-弱交流电网不稳定频率区间及位移变换，作出图2 所示［20，30］Hz 区间内的归一化灵敏度幅频特性及相频特性曲线，该曲线的变化情况可表征参数对直驱式风电场外阻抗特性的影响。由图可知：锁相环参数ki、kp对直驱式风电场的外阻抗特性影响较为显著；而电流内环参数kii、kip对直驱式风电场的外阻抗特性的影响较小；L对直驱式风电场的外阻抗特性的影响在此频段内可忽略不计。且经进一步推导，受锁相环参数ki影响的直驱式风电场的外阻抗特性与受kp影响的直驱式风电场的外阻抗特性的相位差始终为-90°。

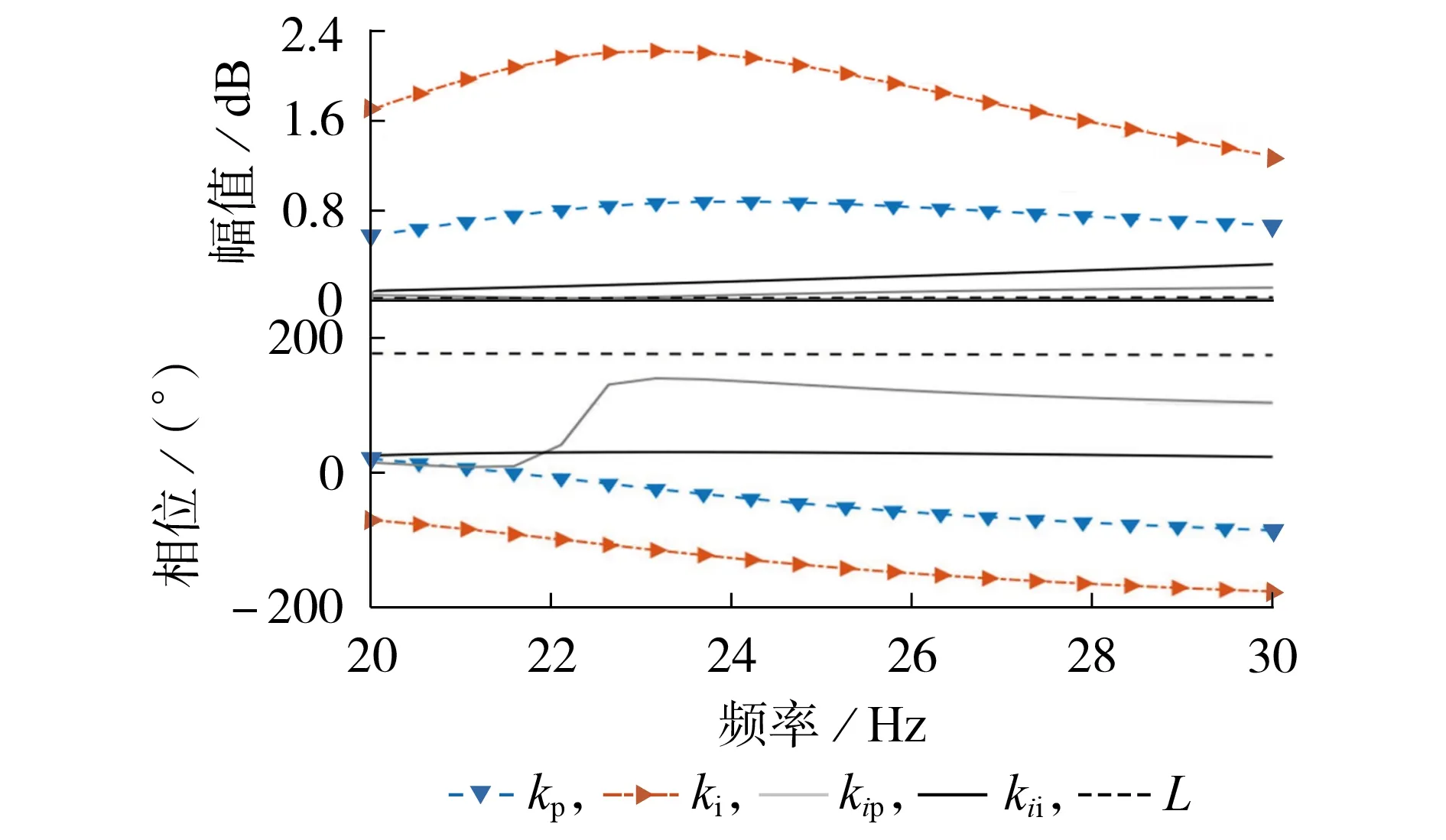
图2 归一化灵敏度的幅频特性及相频特性Fig.2 Characteristics of amplitude-frequency and phase-frequency of normalized sensitivity

2.2 直驱风机分群聚合

从阻抗灵敏度分析结果来看，锁相环参数对直驱式风电场阻抗外特性的影响较为显著，故将其作为分群指标。为清晰起见，以2.1节参数下直驱风机正序端口阻抗Z为对照，将其锁相环比例、积分参数等比例放大后的直驱风机阻抗Z1如图3 所示，阻抗幅值的相对变化量为：

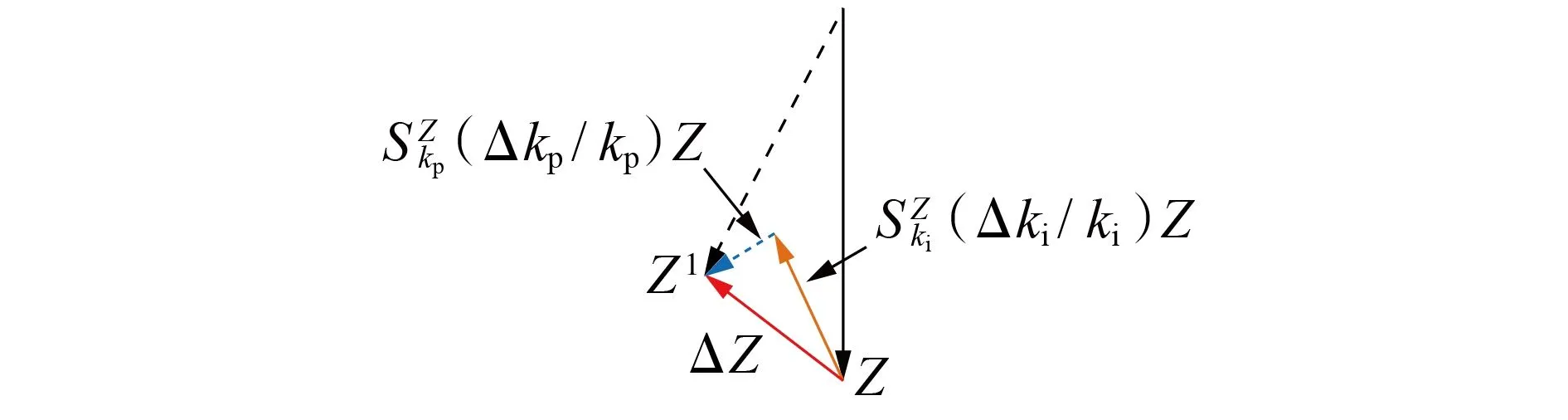
图3 不同锁相环参数下直驱风机阻抗对比Fig.3 Impedance comparison of PMSG under different PLL parameters

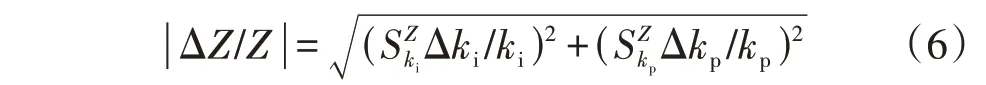
式中：ΔZ为直驱风机锁相环变化带来的阻抗变化量；Δki、Δkp分别为ki、kp的变化量。据2.1 节分析，由于和相频特性始终相差-90°，无论Δki、Δkp如何变化，在［20，30］Hz 区间内，ΔZ/Z总会落在式（6）所示阻抗圆内。综上所述，选取| ΔZ/Z|作为直驱风机的分群指标。

若直驱式风电场控制中心能够获取所有直驱风机的控制参数，则可选取各台直驱风机锁相环参数作为分群指标，对各台直驱风机进行机群划分。显然，为获得较好的等值效果，需使同一机群的锁相环参数呈现明显的中心聚集特征，并建议单个机群中的| ΔZ/Z|不大于5%，这是因为较小的阈值可进一步提高等值精度。

本文选用K-means 算法实现直驱式风电场分群的过程［18］。基于阻抗灵敏度的分析结果，直驱风机分群聚合流程如图4所示。

图4 直驱风机分群聚合流程Fig.4 Flowchart of clustering and aggregation of PMSGs

经过分群后，可以认为同一机群中任意2 台直驱风机由于控制参数差异带来的外阻抗幅值相对误差不会超过5%。值得注意的是，在实际直驱式风电场中不同直驱风机之间较少存在参数I、kp、ki、kip、kii、L完全不同的现象。例如：由于直驱风机变流器批量出厂，同型号的直驱风机L相等；同一批入网直驱风机的并网控制器均采用同一套参数。故式（4）中除了I外，其余参数均相等。按机型和入网批次分群可作为实际工程中的直驱风机分群策略。

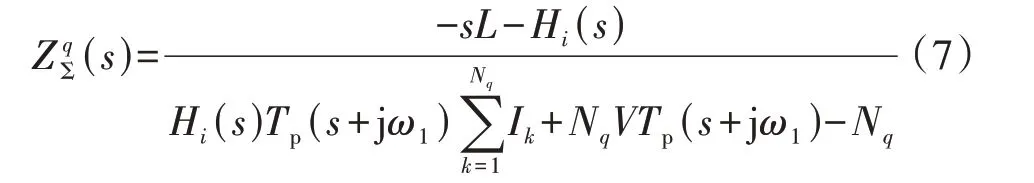
式中：Nq为机群q的直驱风机数量；Ik为机群q中第k台直驱风机的输出电流。从式（7）可以看出，同一机群中的直驱风机在锁相环参数和等效滤波电感参数相等的前提下，Nq并不会影响聚合阻抗表达式的阶数。这说明同一机群中的Nq台风机完全可以用1台直驱风机等效替代，选取合适的参数即可保持等值后的阻抗特性不变。

3 基于遗传算法的直驱式风电场等值降阶方法

数学意义上，大规模直驱式风电场等值过程可转化为对高阶传递函数模型的降阶过程，为满足仿真需要，降阶后的传递函数模型必须为具有式（2）所示结构特征的1 个或多个阻抗并联的模型。常用的模型降阶方法（如平衡截断、Pade 近似等）应用于本文模型时，将出现系数耦合、超定方程求解等问题。

经过上述方法，风电场内的直驱风机可在满足一定误差的条件下分为数群，由式（7）可得同一机群的聚合阻抗。但其格式显然不同于式（2），无法直接得出该机群的等值参数，不具有结构保持特征，需要进一步研究如何将式（7）转换为式（2）所示的参数等值方法。此外，超大规模直驱式风电场中若直驱风机为多批次投产，且厂家类型较多，则其内部直驱风机控制参数差异大，分群聚合后的机群数量可能较多，依然会面临模型阶数较高的问题。

为此，本文提出了一种基于遗传算法的直驱式风电场等值降阶方法，通过建立参数优化模型来获得等值参数。下面对所提方法进行详细说明。

记分群聚合后直驱式风电场的阻抗模型为Z0（s），其可表示为若干式（7）所示聚合阻抗并联的传递函数。设等值后直驱式风电场内共n台等值机，待优化参数为x1、…、xk、…、xn，第k台等值机待优化参数为xk=｛Ik，kp_k，ki_k，kip_k，kii_k，Lk｝。将参数代入式（4），设第k台等值机的阻抗为Z(s，xk)，则n台等值机的总阻抗Zeq(s)为：

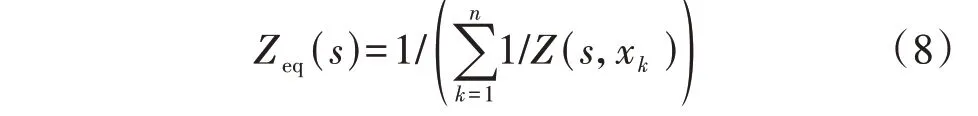
在很大程度上，遗传算法优化效果取决于适应度函数的选取。为保证等值模型和Z0(s)在次同步振荡分析频段具有足够接近的阻抗特性，应该在［0，50］Hz 全频段考察Zeq(s)和Z0(s)阻抗特性的差异性。需特别关注的不稳定频段为［20，30］Hz，以不同频段设置不同采样点的方式进行采样，即［0，20）Hz取10个采样点，［20，30］Hz取30个采样点，（30，50］Hz取10 个采样点。基于此，可以实现在［0，50］Hz 频段内对Z0(s)有较好的逼近效果。此外，采用遗传算法时还应考虑如下因素：工频输出功率的等值，即等值机的总输出电流应等于直驱式风电场总输出电流；控制参数和等值滤波电感均为正数。综上所述，基于遗传算法的参数优化模型如式（9）所示。

式中：f(x)为参数优化函数；sj为第j个离散采样频点；Isum为直驱式风电场总输出电流。

针对直驱风机型号未知或控制参数无法获取的直驱式风电场，通过外加谐波信号扫频的方法实现直驱式风电场外阻抗特性的模拟。尽管此时所得直驱式风电场外阻抗特性是非连续的散点，但是通过本文方法同样可以得到式（9）所示适应度函数，进而实现等值降阶。设置淘汰方式、遗传规则、变异概率等参数后，基于遗传算法选出直驱风机的最优运行参数，并给出等值模型的平均相对误差。

4 算例分析与仿真验证

由于电磁暂态仿真步长为微秒级，本文分别以含5 台相同型号直驱风机和5 台不同型号直驱风机的直驱式风电场为例，基于PSCAD／EMTDC 平台建立仿真模型，运用所提等值方案对该小型直驱式风电场进行等值，并通过扫频模拟直驱式风电场的外阻抗特性，将等值结果与扫频结果进行对比分析，验证等值方案的有效性。

4.1 直驱风机型号相同

假设直驱式风电场内5 台直驱风机型号相同（即除了输出电流外，控制参数和滤波电感参数均相等），5 台直驱风机的输出电流分别为1 800、900、1 500、1 200、750 A，其余参数见附录A 表A1。在模型中省略箱变，5 台直驱风机并联在幅值为565 V 的工频无穷大电源上。

根据式（7），5 台相同型号的直驱风机可以用单台直驱风机等值，为验证这一推论，将上述参数代入式（9），通过遗传算法优化等值机参数。适应度函数随遗传代数的收敛过程如附录A 图A1 所示。由图可知，当种群规模为60、迭代次数约为150 时，单台等值机和5 台相同型号直驱风机的阻抗特性差异在幅值方面很快收敛至1%，这表明对于含有相同型号直驱风机的直驱式风电场，完全可以用1 台等值机等效替代。本算例中得出的等值机参数为：I=6 150 A，kp=0.086 72，ki=32，kip=0.04，kii=82.35，L=0.1465 mH。该算例中等值误差仅为0.6846%。

按照上述参数，在PSCAD／EMTDC 仿真平台分别建立单台等值机和5 台相同型号直驱风机的直驱式风电场的电磁暂态模型，并分别进行仿真扫频。考虑到适应度函数以控制阻抗特性差异的幅值为目标，故此处在［50，100］Hz范围内将等值机与等值前直驱式风电场阻抗模型的相频特性进行对比，如图5 所示。图中，Ztotal为5 台直驱风机并联外阻抗，Zequ为等值机阻抗。由图可知，相同型号1—5号直驱风机尽管输出电流不同（模拟风速不同的实际场景），但其相频特性依旧十分接近。Ztotal与Zequ的相频特性曲线几乎重叠，验证了相同型号的风机可以用单台风机等值的推论，证明了以风速为分群指标、电磁暂态特征保持为目标的传统等值方法并不适用于直驱式风电场并网后的次同步振荡分析。

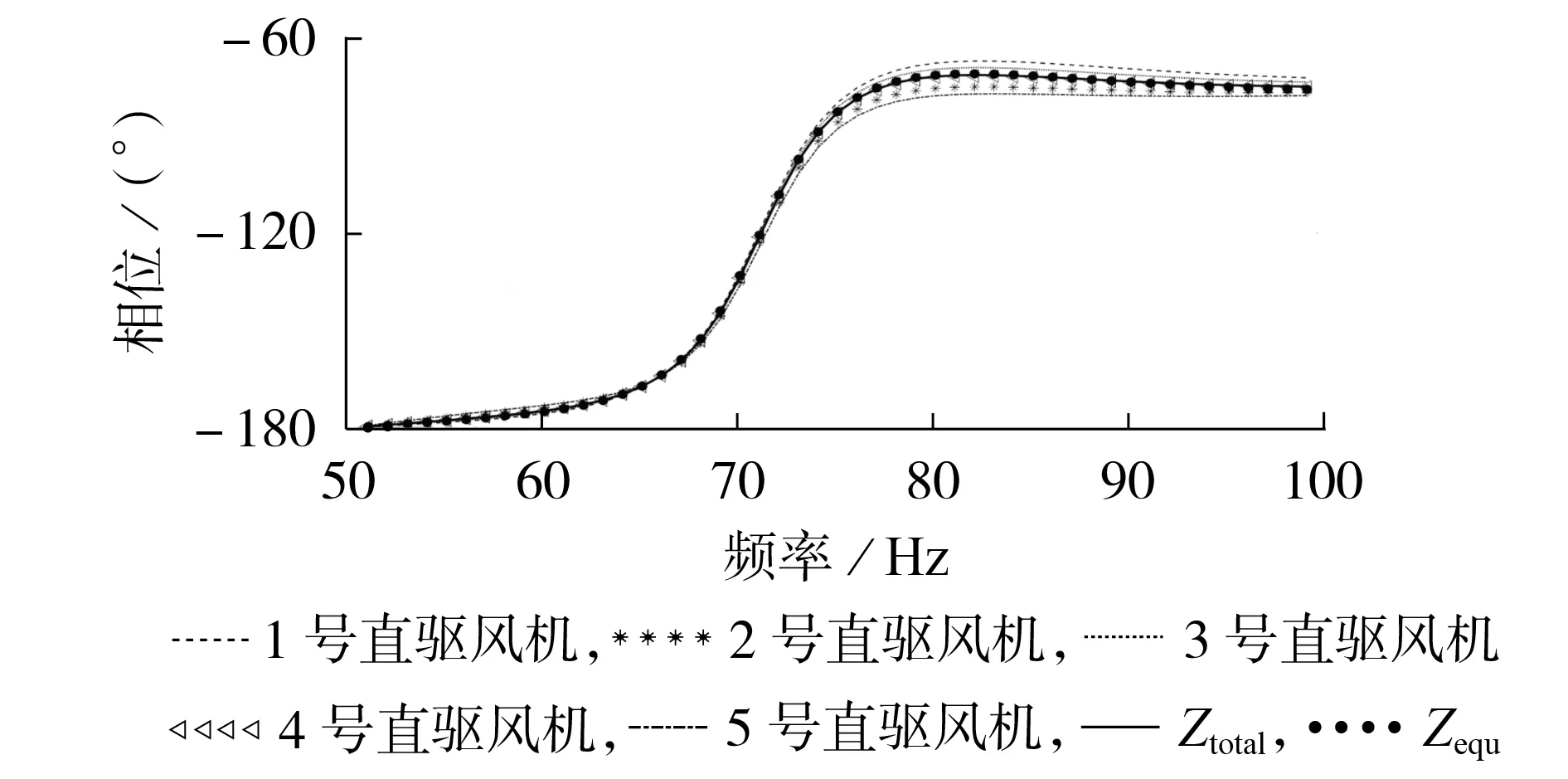
图5 相同型号风机等值前、后的相频特性对比Fig.5 Comparison of phase-frequency characteristics for equivalent model between before and after equivalence of same type of PMSGs

4.2 直驱风机型号不同

假设直驱式风电场内有5 种不同控制参数的直驱风机。由前文分析可知，相同型号机群可以用1台等值机替代，故本节中电磁暂态仿真下5 台等值机参数设置如附录A 表A2所示。为了避免出现“维数灾”的问题，进一步降低等值机台数，将表A2中参数代入式（9），用遗传算法分别优化等值为1、2、3 台等值机的参数，所得降阶后的等值风机优化参数如附录A 表A3 所示。由表A3 可知，当等值机台数分别为1、2、3 时，与原始阻抗模型的幅频特性相比，二者的平均误差百分比分别为10.8%、5.07%、1.89%。

为了验证上述优化参数的实际等值效果，根据附录A 表A2、A3，基于PSCAD／EMTDC 仿真平台分别建立5 台型号不同风机组成的风电场以及等值机台数为1、等值机台数为2、等值机台数为3的风电场阻抗电磁暂态仿真模型，扫频得到其相频特性，对比结果如图6所示，图中Z5to1、Z5to2、Z5to3分别为等值机台数为1—3的等值阻抗。由图可知，不同型号的直驱风机阻抗相频特性差异化明显，其等值降阶具有极大困难。当等值机台数为1 时，其相频特性曲线与Ztotal相比具有明显差异，此时无法实现精确模拟。当等值机台数为2 时，其相频特性曲线能较好地逼近Ztotal的相频特性曲线，且进一步提高等值机台数可以得到更好地实现所提方法的等值效果。

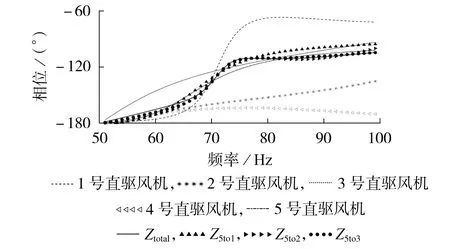
图6 不同型号风机等值前、后相频特性对比Fig.6 Comparison of phase-frequency characteristics for equivalent model before and after equivalence of different types of PMSGs

5 结论

本文基于阻抗法的核心思想，研究了适用于次同步振荡分析研究的直驱式风电场等值方案。首先分析了现有方法的主要弊端，确定等值模型的基本要求。然后提出了基于阻抗灵敏度分析的分群聚合方法，确定了锁相环PI 参数是影响直驱风机外阻抗特性的主要因素，提出了采用K-means 聚类算法的分群方法及按型号分群的实用分群方法。最后利用改进的遗传算法获取等值机的参数，实现了相同型号直驱风机的等值和不同型号直驱风机的降阶。通过仿真扫频对比，证明了本方案所得等值模型完全适用于次同步振荡研究。

附录见本刊网络版（http：//www.epae.cn）。