基于主成分分析的串联电池组故障诊断实用方法

杨启帆，段大卫，李 楠，张玉良，马宏忠

（河海大学 能源与电气学院，江苏 南京 211100）

0 引言

锂离子电池因具有能量密度高、自放电率低、循环寿命长等优势，被广泛应用于电动汽车和电网储能系统［1-2］。近年来，由锂离子电池故障引发的安全事故层出不穷，低安全性成为制约电池发展的首要问题［3］。为了确保电池在不同场景下的安全使用，电池故障诊断研究受到了广泛的关注。然而，目前关于故障诊断的研究大多局限于面向单体电池，面向电池组故障诊断的研究很匮乏。实际上，电动汽车和电网储能系统中成百上千的电池总是以电池组的形式呈现［4-5］，因此开展面向电池组的故障诊断研究至关重要。

电池的单体故障、电池之间的连接故障是电池组中最主要的故障［6］。虽然已有方法分别对电池单体故障［7⁃8］和连接故障［9⁃10］表现出优良的诊断性能，但能否同时兼顾2种故障尚未可知。文献［11⁃12］基于等值电路模型对2 种故障进行了区分，事实上随着电池数量的不断增加，同时涉及大量的物理化学反应过程，为电池组中的每一块电池建立模型并进行精确辨识并不容易，因此这些方法的实用性不强。在实际应用中，电池组的故障仍然是通过电池管理系统提供的阈值法进行诊断［13］。阈值法将实测量与既定阈值进行比较，将超出阈值的实测量记为故障量。实测量一般为电压，而阈值分为绝对阈值和相对阈值，绝对阈值用于监测单块电池的最高、最低电压，而相对阈值用于监测电池间的电压差。阈值法存在以下三方面的缺陷：①无法区分电池单体故障和连接故障；②不能检测未触及阈值的电池单体故障；③阈值固定，未能考虑实测量自身的特点以及多种因素的影响。

在考虑串联电池组内电池电压特点的基础上，本文引入主成分分析PCA（Principle Component Analysis）作为诊断工具。PCA 诊断需要利用历史数据建立模型［14］，而电池实时运行时的电压复杂多变，无法保证历史数据对实时数据全面覆盖，因此为了避免模型失配，提出了PCA 实时建模与故障诊断一体化的思路。PCA 中霍斯林T2（后文简称为T2）统计量和平方预测误差SPE（Squared Prediction Error）统计量的控制限由统计估计法得到，其数值大小取决于数据自身。另外，电池电压之间不存在耦合关系，通过PCA 的变量贡献计算能够准确地判断故障位置。

基于上述PCA 的特性，本文提出了一种面向串联电池组的故障诊断实用方法。首先，设计非硬件冗余的交叉测量拓扑，分别用不同数量的传感器测量电池和连接板；接着，分析组内测量电压的变化特点，利用PCA 提取故障特征并实施诊断；然后，开展实验对所提方法的性能进行验证，同时计及荷电状态SOC（State Of Charge）、健康状态SOH（State Of Health）以及温度差异的影响；最后，利用现场运行数据对所提方法进行测试。

1 故障诊断原理及方案

串联连接是电池组内电池的主要连接形式，由相邻电池的正负极依次连通而成［15］。每块串联电池的电压均可由传感器测量得到，所以开展基于电压的串联电池组故障诊断研究具有普适性。

1.1 交叉测量拓扑

为了区分电池单体故障和连接故障，首先提出了一种非硬件冗余的交叉测量拓扑，如图1 所示。图中：Celli（i=1，2，…）为第i块电池；Li，i+1为Celli与Celli+1之间的连接板；Vi为第i台电压传感器。在测量拓扑中，传感器的测量线与电池的电极直接相连，Vi分别连接至Celli-1的正极和Celli+1的负极，从而保证每块电池仅由1 台传感器测量，且每个连接板由2 台传感器测量。当发生电池单体故障时，故障特征仅传递至单台传感器，而当发生连接板故障时，故障特征会同时传递至2 台传感器，故障位置则需根据接收故障特征的传感器序号进行确定。需要指出的是，相比于目前电池与传感器一对一的测量拓扑，图1 所示的交叉测量拓扑并不需要增加额外的传感器或者扩增电压传感器的量程。

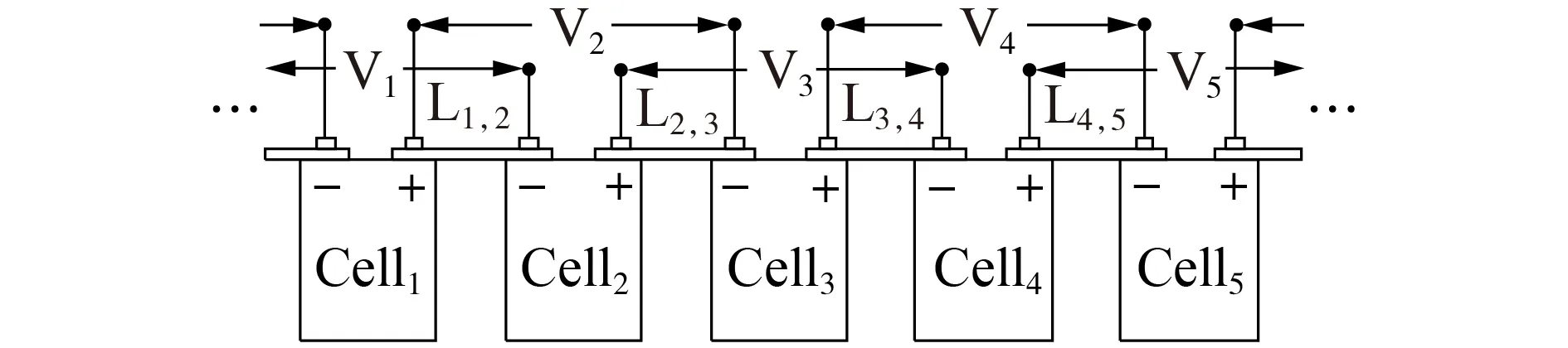
图1 交叉测量拓扑Fig.1 Cross-measurement topology

1.2 基于PCA的故障诊断技术

1.2.1 PCA的理论基础

本文采用PCA 对电池组内的故障特征进行提取，首先对基于PCA 进行故障诊断的主要思想和计算流程进行描述。

主要思想为：采用PCA 将原始数据从高维空间投影至2 个低维子空间，分别为主元子空间和残差子空间。原始数据在主元子空间和残差子空间的投影分别对应原始数据中的主要信息和与主要信息相悖的误差信息。主元子空间的信息可以近似地表达原始数据的信息。根据主元的选取，构建PCA 模型。基于PCA 的故障诊断是根据PCA 模型的T2和SPE 统计量进行的，一般先根据历史正常数据构建PCA 模型，并计算T2和SPE 的控制限，然后将实时数据代入模型计算得到T2和SPE 统计量，如果统计量大于控制限，则认为发生故障。

计算流程如下：令数据矩阵为x=[xi(k)]N×J（k=1，2，…，N；i=1，2，…，J；J为变量个数；N为样本个数），先按照式（1）—（3）对矩阵x进行标准化处理。

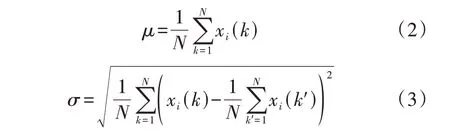
式中：μ、σ分别为矩阵x的第i列xi的均值、标准差；x'i(k)为第k行第i列元素的标准化数值。将标准化数值x'i(k)构成的矩阵记为X，则PCA模型可表示为：

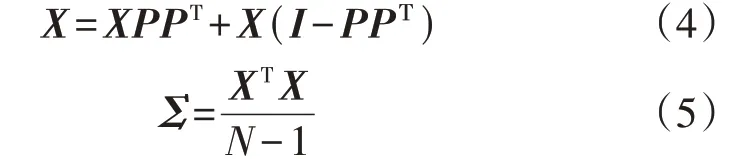
式中：I为单位矩阵；P为负荷矩阵，根据X的协方差矩阵Σ（J×J阶）确定，Σ的计算式见式（5）。式（4）等号右侧的第1 项表示数据向主元子空间的投影，第2 项表示数据向残差子空间的投影。

对Σ进行奇异值分解：

式中：pi（J×1 阶）、λi分别为Σ的第i个特征向量、特征值，且有λ1≥λ2≥…≥λJ。通常采用累积百分比选取前l个pi，则P为：

当检验水平为α（通常取值为95%）时，T2统计量的控制限γT2，lim和SPE 统计量的控制限γSPE，lim分别如式（8）和式（9）所示［16］。

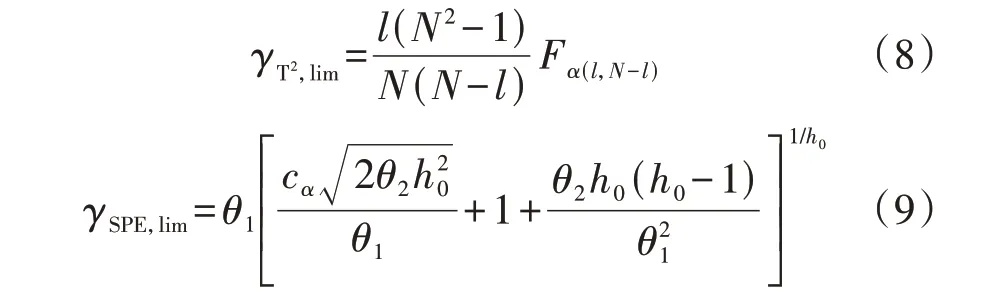
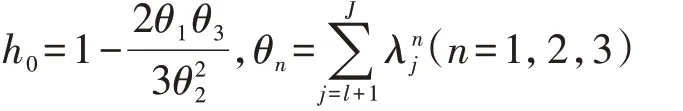
由式（8）、（9）可见，γT2，lim和γSPE，lim的大小是由数据自身特性决定的。

1.2.2 基于PCA的故障诊断

基于PCA 进行故障诊断时，存在统计量选取和模型适配2 个关键问题，本节结合串联电池组内电池电压的特点，对这2个关键问题进行讨论。

5 个串联电池在联邦城市行驶工况下的电压曲线见附录A 图A1。由图可见，高相关性和强多变性为串联电池组内电池电压的两大特点：组内相同型号的电池具有相近的开路电压和内阻，当接收到同一电流指令后，电池电压表现出高相关性；电动汽车的行驶习惯和储能系统的运营方式并不固定，因此电池电压复杂多变。

虽然T2和SPE 都被用于故障诊断，但两者的物理意义有所不同。T2衡量的是变量整体趋势被改变的情况，而SPE 衡量的是破坏变量整体趋势的局部情况。为了便于理解，图2 给出了T2和SPE 用于故障诊断时的区别，其中左图中的点划线表示整体趋势，实线表示趋势的破坏情况。图中，γT2、γSPE分别为T2统计量、SPE统计量。

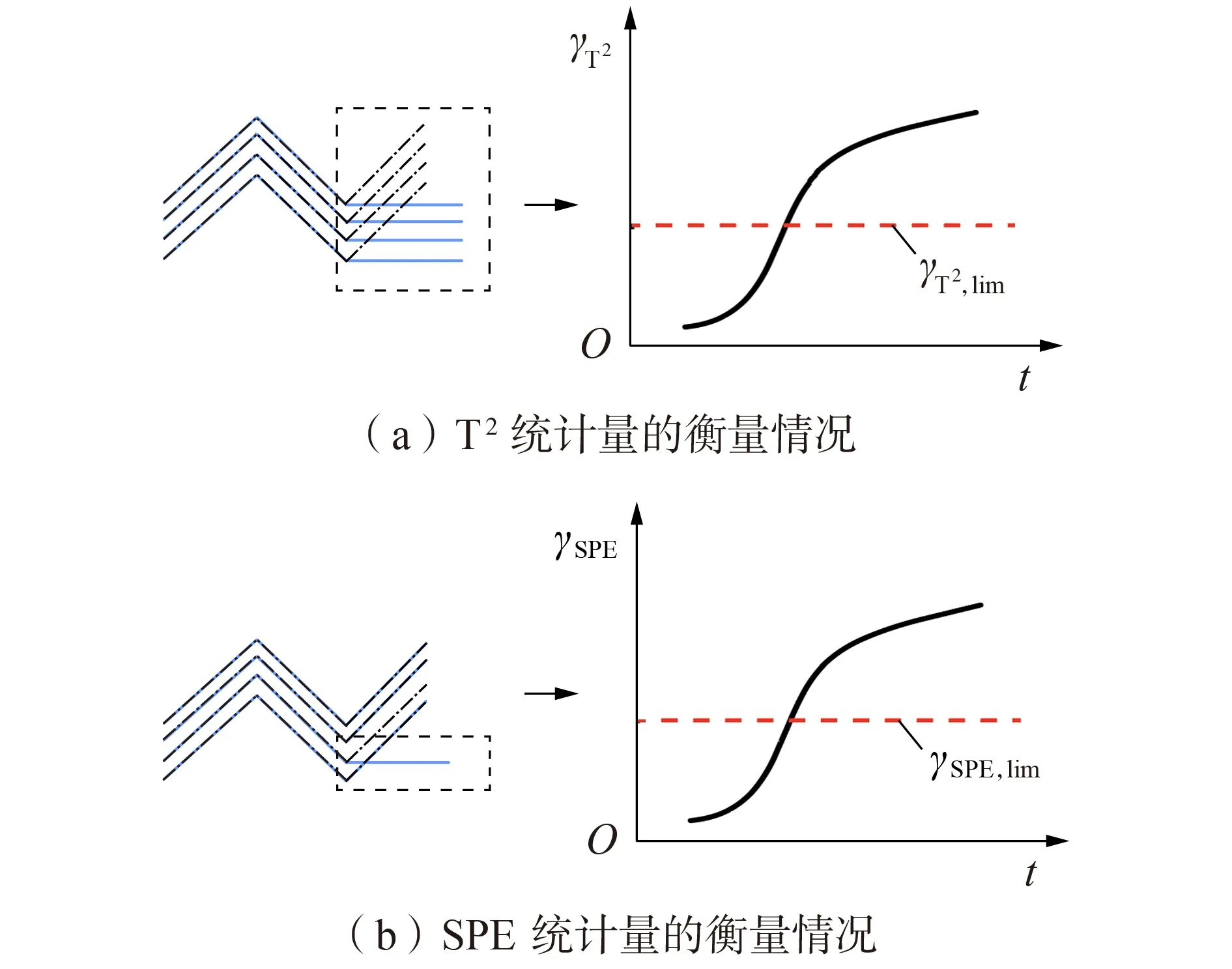
图2 T2和SPE用于故障诊断的区别Fig.2 Difference between T2 and SPE for fault diagnosis

事实上，对于串联电池组中的电池和连接板而言，仅会有1 个或者少数几个发生故障。如果将组内每台传感器的测量电压Vi看作1 个变量，则仅有少数的故障电压表现出不符合高相关性的特点，而整体电压趋势不会被改变，因此选用SPE 统计量进行故障诊断更加合理。令标准化的数据向量为z（1×J阶），则SPE统计量γSPE为［16］：

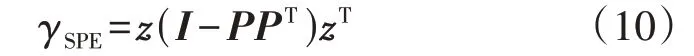
若满足式（11），则表示故障被检测。

进一步地，根据式（12）计算z的每个变量zi（i=1，2，…，J）对γSPE的贡献。

如前文所述，PCA 模型一般由历史正常数据构建得到，这要求历史正常数据足够丰富以确保所建模型能尽可能地适应全部的实时正常数据。然而，电池电压的强多变性决定了历史正常数据无法全面反映实时正常数据的变化，因此PCA 存在模型失配问题。为此，本文提出了PCA 实时建模与故障诊断一体化的思路，即利用实时数据构建的模型来检测实时数据的故障情况。该思路的依据为：①同一组数据可天然避免模型失配；②组内电池电压的强相关性信息唯一反映在协方差矩阵中的最大特征值内，当采用最大特征值对应的特征向量实时构建模型时，模型的故障诊断能力不会下降。

此外，由图A1 还可以看出，多条电压曲线并非完全重合，这表明电池之间存在一定的不一致性。研究结果表明［17］，电池之间的不一致性表现在电压上主要为幅值和偏置的差异，可直观看出图2 中的电压曲线也满足这一特点。但是，根据式（1）—（3）所示的标准化处理过程可知，电池之间的不一致性并不会影响PCA 计算，这是因为幅值和偏置的差异在标准化过程中被消除。

1.3 故障诊断方案

基于交叉测量拓扑和PCA 故障诊断技术，面向组内电池单体故障和连接故障的实用诊断方案流程图如图3 所示，流程在每个采样中断实现。具体的故障诊断步骤见附录B。

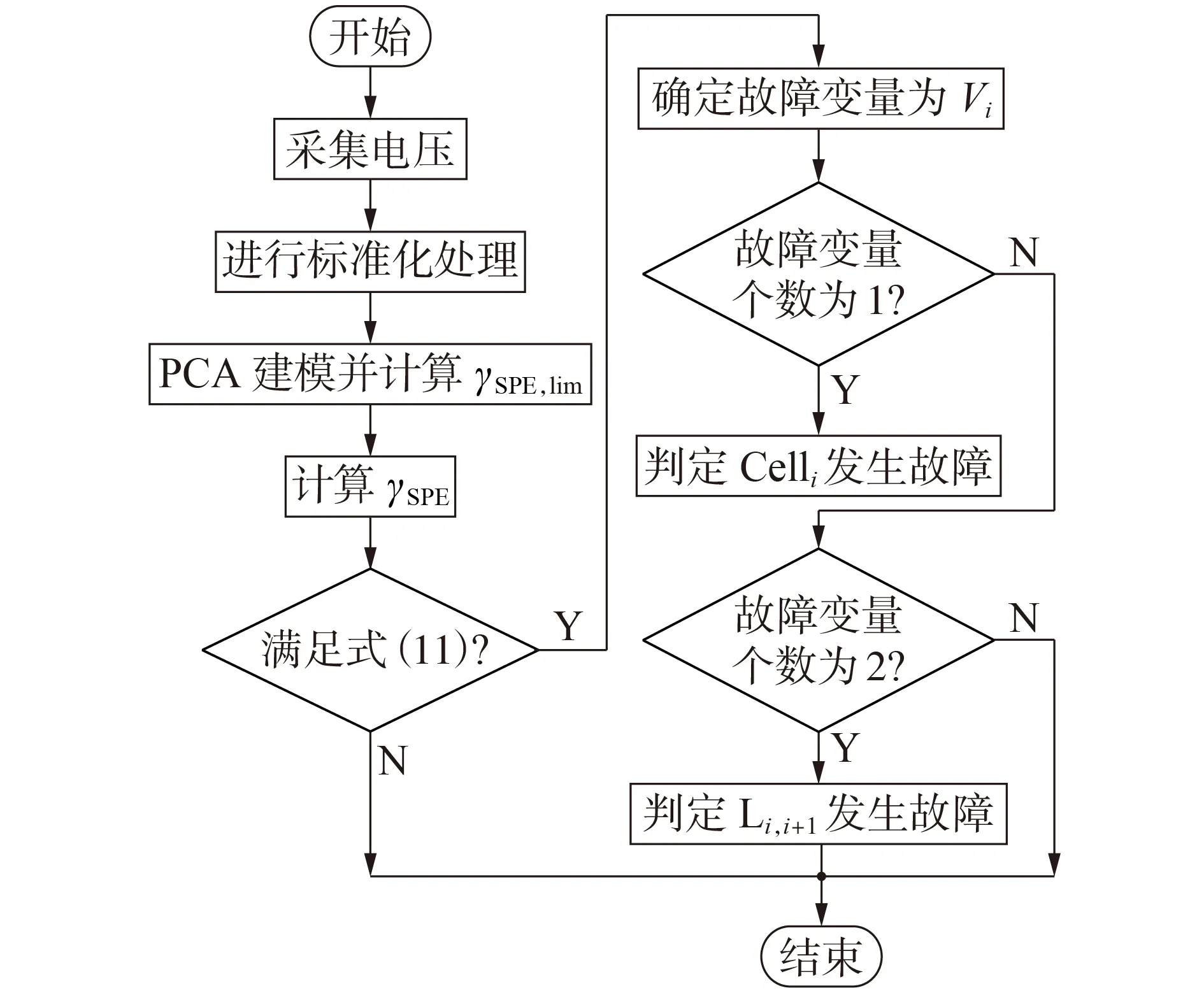
图3 故障诊断流程图Fig.3 Flowchart of fault diagnosis

组内电压的采集数据量由数据窗长决定。具体应用时，窗内数据应能准确地反映电压之间的相关性，通过观测实验数据和现场运行数据，本文将窗长选定为30 个数据点。需要指出的是，基于PCA 进行故障诊断时，故障数据只要出现无法适应模型的情况就能发出动作信号，并不需要故障数据完全填满数据窗，因此故障诊断具有较好的实时性。此外，相较于固定阈值的阈值法，γSPE，lim根据数据特点在每个数据窗内不断更新，这使得本文所提方法的阈值具备自适应调整的能力。

2 实验验证分析

2.1 实验条件

以5 块圆柱型磷酸铁锂电池作为实验对象，参数见附录C 表C1，实验设备见附录C 图C1。利用Arbin测试仪充放电池并测量电池电压，频率为1 Hz。恒温箱将实验温度控制为25 ℃。5块电池通过夹具串联连接，传感器按照图1 所示拓扑布置。每次实验前，电池采用恒流充电至3.45 V 并静止1 h。所有实验均在城市动态行驶工况下进行。实验方法和参数主要参考近5 a的电池故障相关研究［12，18⁃21］。

2.2 故障诊断方案的实用化

正常运行工况下串联电池的电压曲线和PCA故障诊断结果分别见附录D 图D1 和图4。由图D1可知：电池之间存在一定的不一致性，显然基于单一模型的故障诊断方法很难同时兼顾多块电池的状态；大约在197 s 时最大电压差超过0.02 V，如果相对阈值整定过小，则会引起诊断虚警。由图4（a）可知，本文所提方法的阈值γSPE，lim不再固定，而是能够随着数据自适应调整。然而，受到电池不一致性和测量噪声的影响，测量电压存在非相关变化，引起较多γSPE>γSPE，lim的情况。为了保证本文所提方法的实用性，采取2 种实用化手段提高容错能力：①小幅度提高控制限γSPE，lim，即在γSPE，lim的基础上增加ε，并设ε取值为0.01；②采用连续β点的判断逻辑，β取值为3，即当且仅当连续3 次及以上满足式（11）时，才发出故障信号。ε和β的取值说明见附录E。采取实用化手段①后的故障诊断结果见图4（b），可以看出仅存在个别γSPE>γSPE，lim的情况，但均不满足连续3点的判断逻辑，即不满足采取实用化手段②的条件。可见，采取实用化手段后，本文所提方法在正常情况下能够可靠不发出故障信号。

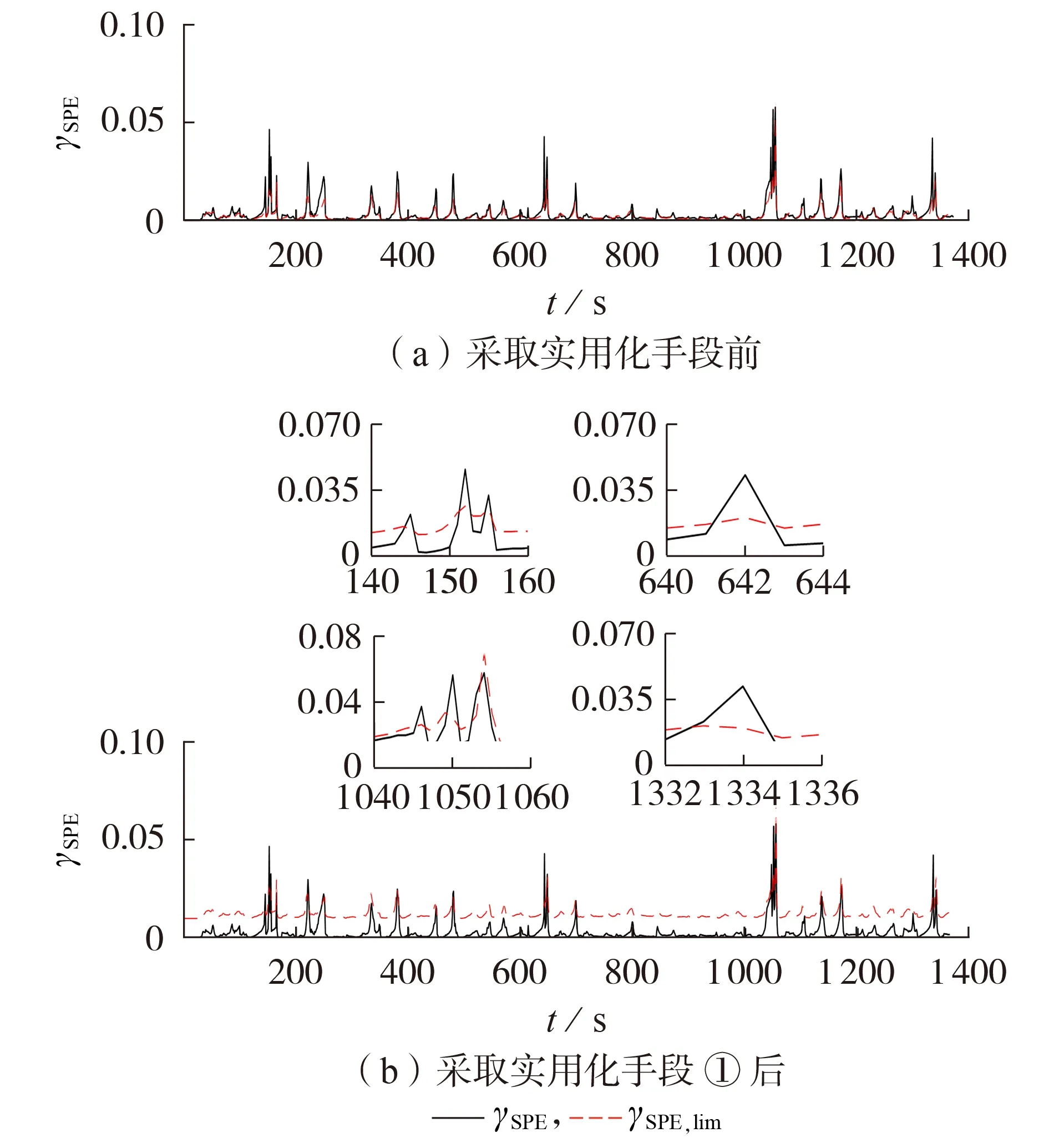
图4 正常运行工况下的PCA故障诊断结果Fig.4 Fault diagnosis results based on PCA under normal operation condition

2.3 电池单体故障

短路是电池的典型故障［22］，本文通过向Cell4的正负极并联5 Ω 电阻模拟短路故障，故障时间为604～720 s，该工况下的电压曲线和PCA 故障诊断结果分别见附录F图F1和图5。

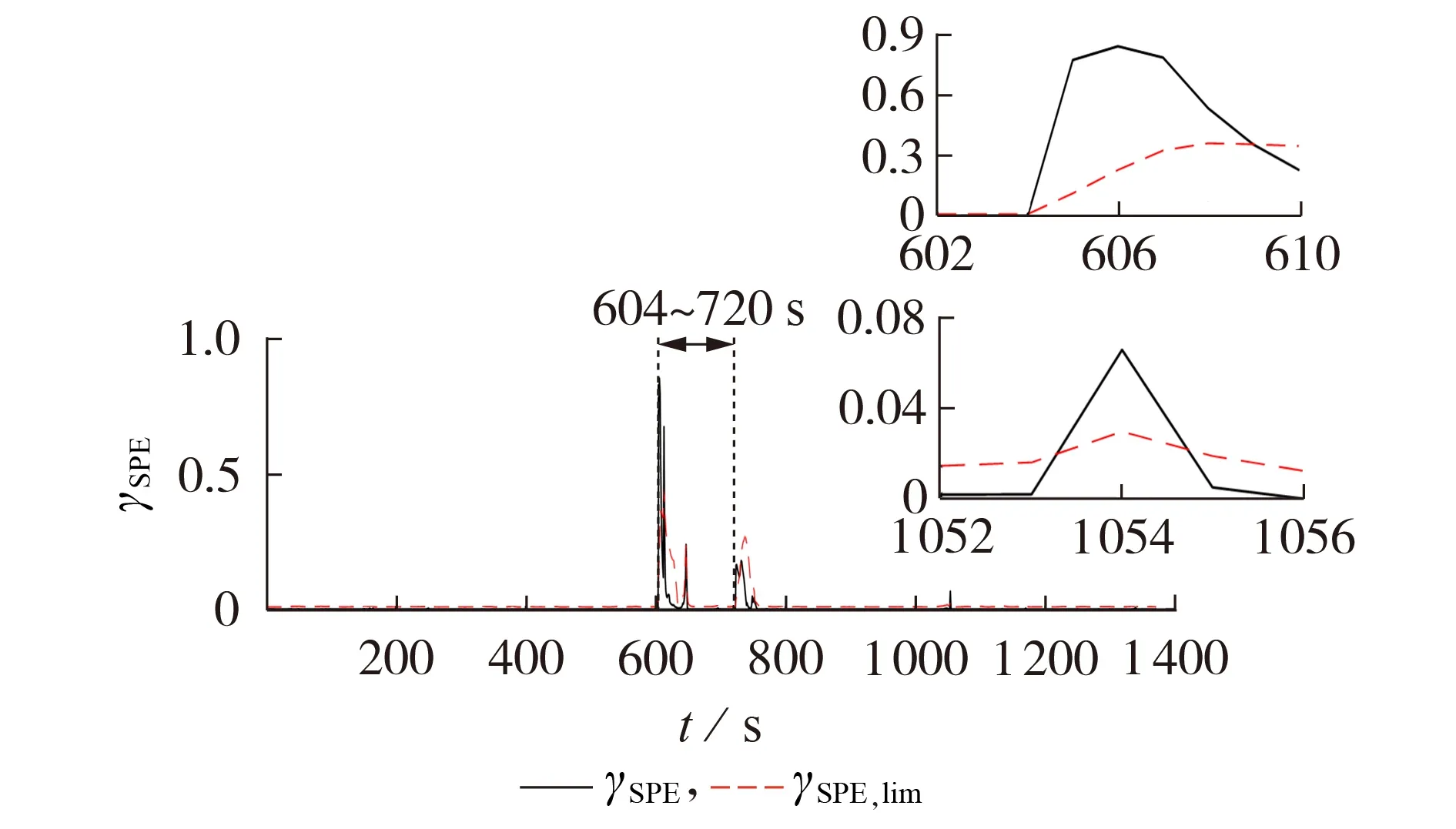
图5 电池单体故障的PCA诊断结果Fig.5 Battery cell fault diagnosis results based on PCA

由图F1（a）可见，V4在604 s时开始下降，故障期间V4降落幅度较小，最小电压值约为3.2 V，仍然高于表C1中的下限截止电压，因此绝对阈值法无法检测该短路故障。由图5 可知，γSPE在604 s 后显著增大并快速超过γSPE，lim，在之后的5 s 内，γSPE始终大于γSPE，lim，由1.3节中的故障诊断方案可知，此时判断串联电池组内发生故障。由图F1（b）可知，604 s 后γSPE，4高于平均水平（γSPE的平均水平由透明平面表示），表明γSPE，4对整体γSPE的贡献最大，因此V4为故障变量。V4由传感器V4测量得到，由图1 所示交叉测量拓扑可知，仅Cell4的故障特征会唯一反映在V4上，因此可以诊断Cell4发生故障。此外，1054 s时出现γSPE>γSPE，lim的情况，不过由连续3 点判断逻辑可知，此时本文所提方法不会发生虚警。

2.4 连接故障

电动汽车在恶劣道路工况下容易发生电池之间的连接故障，造成电池组功率衰退、局部过热等负面影响［12］。通过增大Cell2与Cell3之间连接板L2，3的电阻来模拟连接故障，将L2，3的电阻设定为0.07 Ω，数值约为故障前的2 倍。故障时间为295～600 s 和900～1 371 s，该工况下的电压曲线和PCA 故障诊断结果分别见附录F图F2和图6。

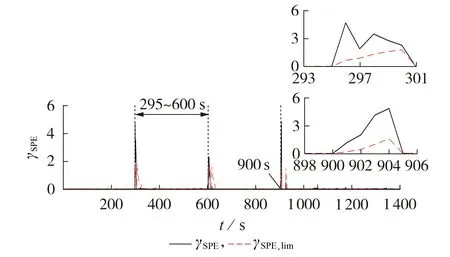
图6 连接故障的PCA诊断结果Fig.6 Connection fault diagnosis results based on PCA

由图F2（a）可知，故障过程中V2和V3同时表现出更加明显的波动，加剧了电池之间的不一致性。由图6 可见，γSPE分别在295 s 和900 s 时开始快速增大并迅速超过γSPE，lim，在之后的5 s 内，γSPE始终大于γSPE，lim，据此可以判断电池组内发生故障。由图F2（b）可知，2 次故障下γSPE，2和γSPE，3均高于γSPE的平均水平，表明V2和V3为故障变量。V2和V3分别由V2和V3测量得到，而L2，3是V2和V3测量的交叉部分，故可以诊断L2，3出现异常。

2.5 影响因素分析

2.3节和2.4节证明了本文所提方法能够可靠地区分电池单体故障和连接故障，本节将进一步对所提方法的性能进行验证，主要考虑SOC、SOH 以及温度差异的影响。文献［19⁃20］对行驶3 a、里程为35 000 km 的电动汽车电池组进行拆解，发现电池之间的SOC 和SOH 差异可分别达到13%和3%。文献［20］分析了温度对电池组功率衰退的影响，并考虑了15 ℃的温差。为此，本文考虑20%的SOC 差异、3.9%的SOH 差异和15 ℃的温差，选用3 块电池（电池A、B、C）进行实验，电池参数见表1。实验中，将电池A 作为参考，电池B、C 用于设置差异，实验参数如表1 所示。SOC 通过控制满充电池的放电时间进行设定，温度通过恒温箱控制。电池A、B为2块具有额定容量的全新电池，电池C为经历过400 次循环的旧电池，容量为3.652 A·h。不同影响因素下的电压曲线和PCA 故障诊断结果分别见附录F图F3—F5和图7。

表1 实验参数Table 1 Experimental parameters

由图F3—F5 和图7 可知：当SOC 差异达到20%、SOH 差异接近4%且温差达到15 ℃时，γSPE均能可靠小于γSPE，lim，这表明本文所提方法对组内电池的SOC、SOH 以及温度差异具有充足的鲁棒性；电池SOC越高，则电压数值越大，SOH越低，则电压波动越明显，低温相较于高温对电池电压的影响更加显著。

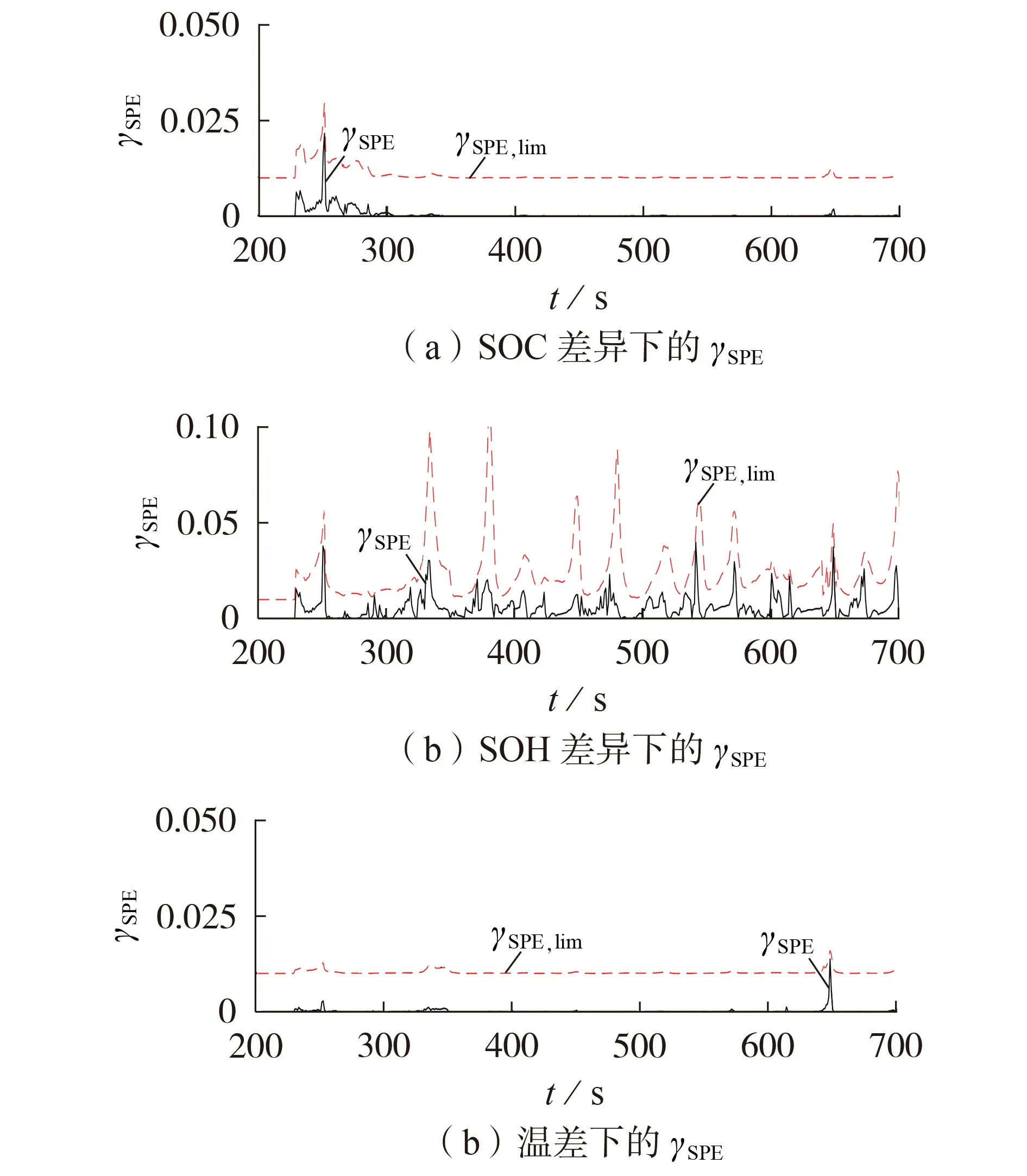
图7 不同影响因素下的PCA故障诊断结果Fig.7 Fault diagnosis results based on PCA with different influence factors

3 现场数据测试

利用某电池储能电站的现场运行数据进行测试。电池组由6 块电池串联而成，电池管理单元对每块电池的电压进行测量以及监测，其中电压过高的一级阈值为3.4 V，报文动作为报警，测量频率为1/30 Hz。现场数据的10 h 运行曲线及PCA 故障诊断结果分别见附录F 图F6 和图8。由图F6 可见，电池电压在6 h 至7 h 内频繁地触碰一级阈值3.4 V，引起电池管理单元多次报警，但由电压之间的相关性可以判断此时并未发生故障，即不应发出报警信号。由图8可见，10 h内的γSPE可靠小于γSPE，lim，表明本文所提方法能够有效避免发生虚警。

图8 现场运行数据的PCA故障诊断结果Fig.8 Fault diagnosis results based on PCA with field operation data

4 结论

本文提出了一种面向串联电池组的实用故障诊断方法，能够准确地区分电池单体故障和连接故障，所得结论如下：

1）综合利用交叉测量拓扑和PCA 提取故障特征并实施故障诊断，所提交叉测量拓扑无需额外增加传感器或者扩展传感器量程，所用PCA 将实时建模与故障诊断一体化，有效避免了模型失配问题；

2）所提方法具备良好的实用性能，无需多电池建模，设定的阈值具备自适应电压变化的调整能力，对阈值法无法检测的电池单体故障有充足的反应能力，对SOC、SOH以及温度差异有足够的鲁棒性；

3）基于实验数据和现场运行数据验证了本文所提的有效性和性能优越性。

附录见本刊网络版（http：//www.epae.cn）。