基于几何关系求解的汽轮发电机定子接地故障定位方法

裴丽秋，杨洪涛，张琦雪，李华忠，许林波，吴礼军，陈 俊，4

（1. 淮浙电力有限责任公司凤台发电分公司，安徽 淮南 232131；2. 南京南瑞继保电气有限公司，江苏 南京 211102；3. 浙江浙能技术研究院有限公司，浙江 杭州 311100；4. 东南大学 电气工程学院，江苏 南京 210096）

0 引言

大型同步发电机定子接地故障定位一直是行业内研究的热点难题［1⁃2］。传统的人工排查方法包括加压观察法、分割法、直流电桥法、开口变压器法等，采用上述方法进行综合判断能较好地实现定子接地故障定位，但存在耗时长、排查效率低、试错次数多等问题，尤其是对于定子槽数较多的发电机，耗时越长，则发电量损失越大。而对于通常采用基波零序电压、三次谐波比率、注入低频信号等原理的继电保护设备［3⁃4］，虽然已在现场得到成熟应用，但只有在发生金属性定子接地故障时基波零序电压定子接地保护才能准确判断故障位置。文献［5⁃7］提出的基于零序方向的选择性定子接地保护虽然能区分故障发生在发电机定子内部还是外部，在一定程度上提高了排查效率，但发电机本体即定子绕组的接地故障定位还有待进一步的研究。发电机定子绕组局部放电在线监测设备［8⁃9］虽然能通过监测局部放电信号量的变化对导体绝缘下降情况进行实时监测，但也无法实现定子接地故障定位功能。因此如何快速地定位定子接地故障，提高排查效率，是现场亟待解决和用户关心的问题。

文献［10］提出了一种定子单相接地故障定位方法，建立了接地故障位置与定子零序电压、定子绕组对地电容及接地电阻间的函数关系，并进行了故障位置的计算，但实现该方法的前提是定子接地电阻为已知且是准确的。文献［11］提出了一种不依赖于注入式定子接地保护原理的定子单相接地故障定位方法，该方法采用定子绕组三相机端、零序电压及发电机组参数之间的关系求解接地电阻值和定子接地故障位置，但其未考虑定子绕组基波电势分布特征、接地变压器短路阻抗等因素的影响，从而导致计算结果存在偏差［12］。文献［13］考虑了定子绕组基波电势分布特征，建立了定子接地故障位置、基波电势及绕组相电势的近似三角函数关系，且假设当绕组电势的相位角θ较小时，存在tanθ≈θ关系，从而计算故障位置，该方法在θ较小，即故障位置靠近机端时具有较高的精度，但故障位置越靠近中性点，误差越大。

本文分析了发生汽轮发电机定子接地故障时，定子绕组基波电势、基波零序电压、接地电阻及零序回路阻抗特征参数之间的关系，并考虑定子绕组内部基波电势分布特征，在同一平面上建立了故障位置至中性点的基波电势与定子基波零序电压、机端绕组相电压等相量间的几何关系，从而计算中性点至故障位置对应的故障角，最终实现了定子接地故障位置及接地电阻阻值的计算。

1 回路分析与基本原理

1.1 等值回路分析

假设故障前发电机以额定电压运行，每相绕组对地电容相等，A 相定子接地故障原理图如图1 所示。图中：T 为接地变压器；EA、EB、Ec分别为发电机A、B、C 相机端绕组相电压；C∑为等效至机端的定子绕组每相对地电容，包括定子绕组本身的对地电容以及与之并联的机端其他设备的对地电容；rn为接地变压器二次负载电阻，其折算至一次侧的阻值为RN；α为定子绕组中性点N至故障点的匝数占一相单分支串联总匝数的百分比；E(α)为A 相定子接地故障点至中性点间的电势；RF为接地电阻。

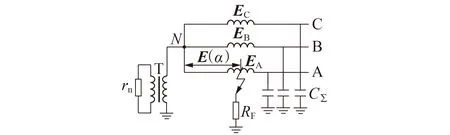
图1 发电机定子绕组单相接地故障原理图Fig.1 Principle diagram of single-phase grounding fault of generator stator winding

考虑到接地变压器为非理想变压器，利用简化短路阻抗一次值ZK=RK+jXK对其进行等效，其中RK、XK分别为接地变压器的短路电阻、电抗。同时忽略发电机定子绕组电阻及电抗，从而对图1 简化得到基波零序等效电路，如图2所示。图中：U0为发电机零序电压；Req、XCeq为零序回路阻抗特征参数。

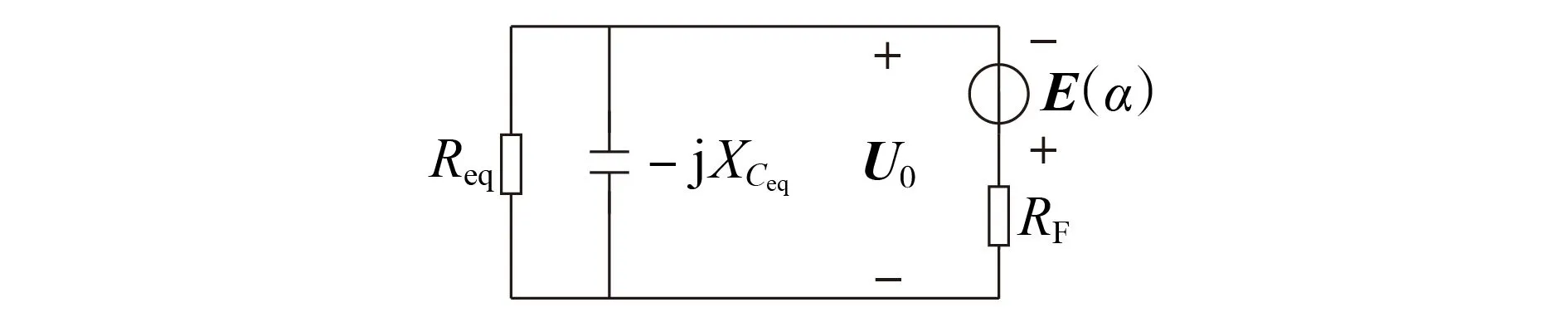
图2 基波零序等效电路图Fig.2 Fundamental wave zero-sequence equivalent circuit

此时发电机零序电压计算公式为：

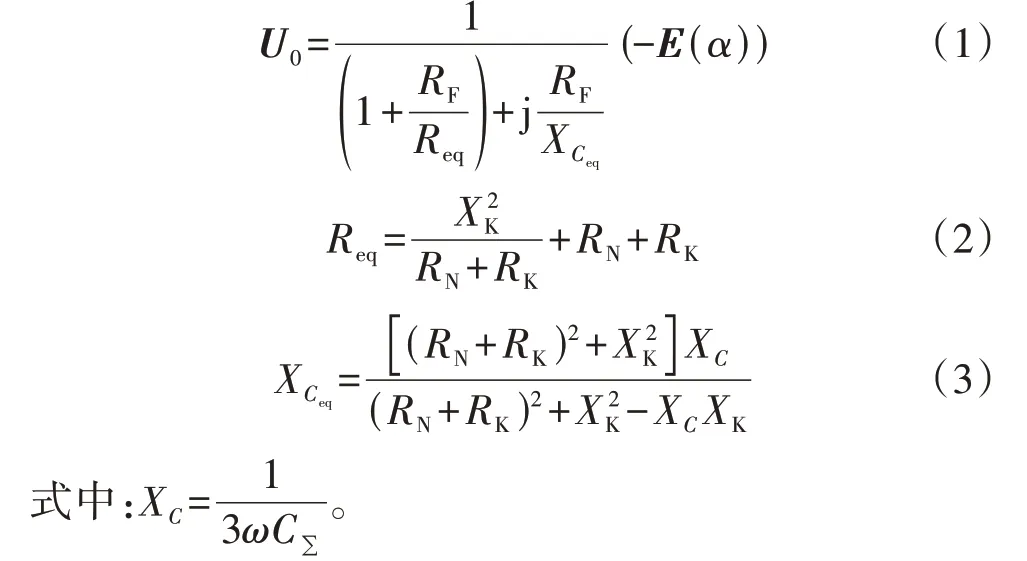
在传统定子接地故障定位方法中，不考虑定子绕组各分支基波电势的分布特征，将E(α)≈αEA代入式（1），推导得到定子接地故障位置α的计算公式为：

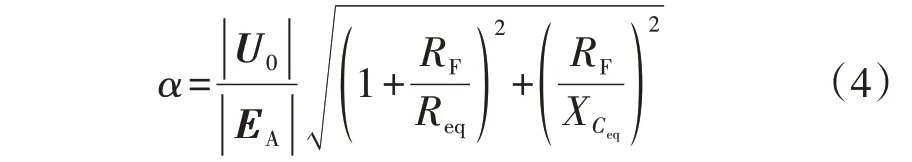
将实测零序电压、接地电阻及故障相绕组电压代入式（4），即可计算出相应的定子接地故障位置。

然而，上述方法未考虑以下2个方面的问题。

1）大型发电机定子绕组内部电势呈现分布特征，存在E(α)≠αEA的情况，以A 电厂660 MW 汽轮发电机为例，发电机定子绕组基波电势示意图如图3 所示。由图可见，定子接地故障点至发电机中性点的电势E(α)与机端绕组电压αEA的相位和幅值存在差别，若采用式（4）进行计算，则将导致计算结果与理论值存在一定误差。

图3 发电机定子绕组基波电势示意图Fig.3 Schematic diagram of fundamental wave potential of generator stator winding

2）计算结果完全依赖于实测接地电阻阻值。由式（4）可知，计算定子接地故障位置需要准确的接地电阻阻值。目前接地电阻阻值测量均采用注入式定子接地保护实现［14⁃16］，当在靠近机端处发生接地电阻较小的定子接地故障时，注入式定子接地保护测量的电压、电流信号中同时存在较大的工频分量，导致注入式定子接地保护实测的接地电阻阻值不准确。另外，对于没有配置注入式定子接地保护的场合，例如发电机中性点不接地或者经消弧线圈接地方式下，该方法也无法直接使用。

1.2 基本原理

根据发电机定子绕组内部基波电势分布特征，从中性点N出发，将其电势相量依次相连，可近似等效为平面上的一段圆弧［17］。以A 电厂660 MW 汽轮发电机为例，假设定子绕组A1 分支内部点E发生接地故障，接地电阻为RF，此时E(α)即为确定值，电压相量间的几何关系示意图如图4所示。图中：点A为A1 分支机端；点D为地电位点对应E(α)对应U0对应EA；A1 分支绕组内部基波电势依次相连后形成圆弧，其圆心为O1，根据定子绕组内部排布情况及文献［17］的方法计算的圆心角∠NO1A，记为β。

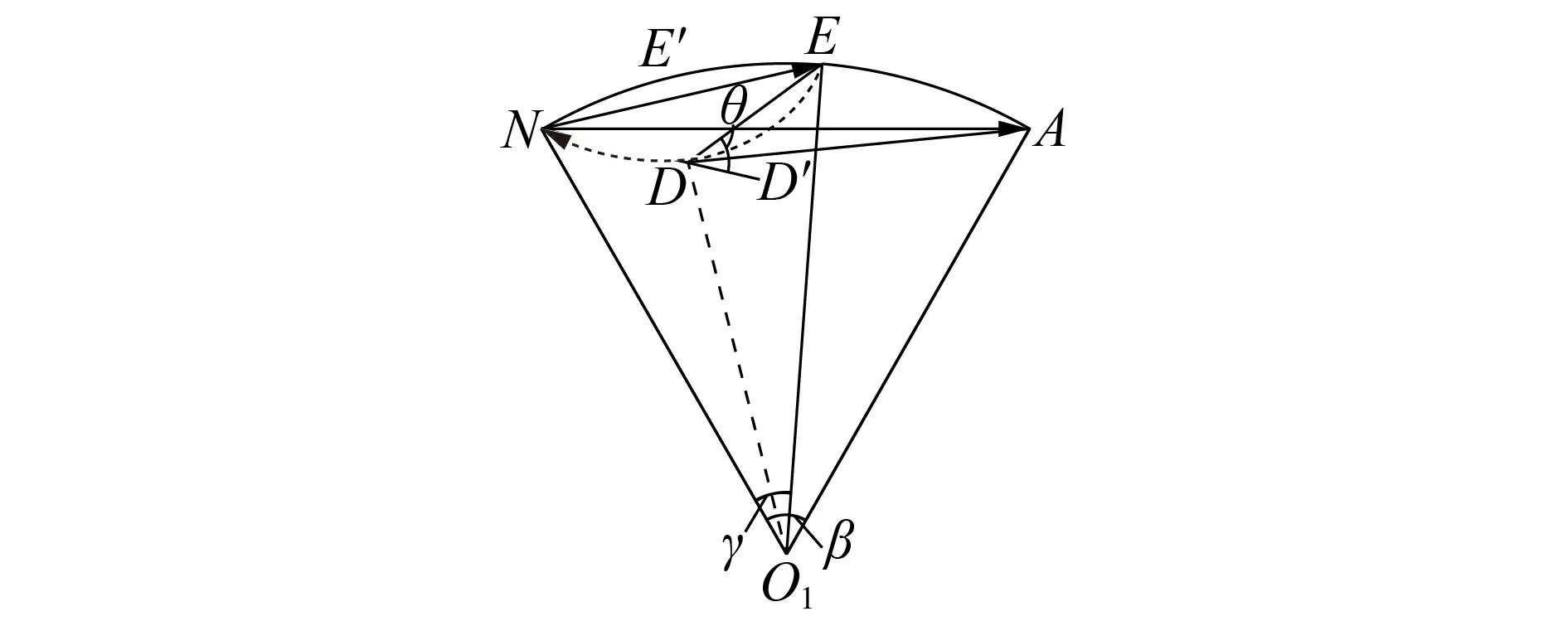
图4 发生定子接地故障时电压相量间的几何关系示意图Fig.4 Schematic diagram of geometric relationship among voltage phasors when generator stator winding grounding fault occurs

根据式（1），当RF在［0，+∞）Ω 范围内变化时，对应U0在［-E(α)，0］范围内变化，U0轨迹（即地电位点D的运动轨迹）是以E(α)为弦的一段圆弧，如图4 中虚线标记的圆弧所示。可知，当RF 越小时点D越靠近点E，当RF越大时点D越靠近点N。根据已知的及零序回路阻抗特征参数值等，计算此时圆弧͡对应的圆心角γ，即故障角。当定子绕组A1分支发生接地故障时，故障位置均会落在圆弧上，若故障点E从中性点N逐渐变化至机端点A时，故障角γ对应的变化范围为［0，β］，以圆弧全长NA对应的圆心角β作为基准（100%），则γ与β的比值即为当前的定子接地故障位置。得到γ后，利用各相量间的关系即可求出E(α)，然后根据式（1）求解对应的RF。

2 定子接地故障定位新判据

由前文可知，求解故障角γ为本文所提基本原理的关键所在，因此本文提出一种基于几何关系求解的定子接地故障定位方法，具体步骤如下。

1）判断定子接地故障相。对于发电机中性点经高阻接地的机组，当其满足Req≤XCeq时，可依据接地故障相电压幅值最低原理，判断出相应的故障相；对于中性点不接地或经消弧线圈接地的发电机，可采用文献［1］介绍的原理实现故障相判别。

2）计算故障角γ。假设A相定子绕组A1分支点E处发生接地故障，如图4 所示，根据已知机端相电压、定子零序电压，可求得。根据圆心角β可得：

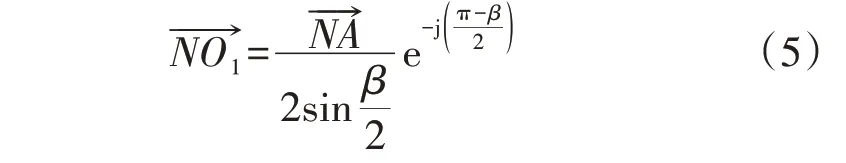
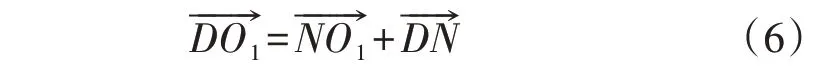
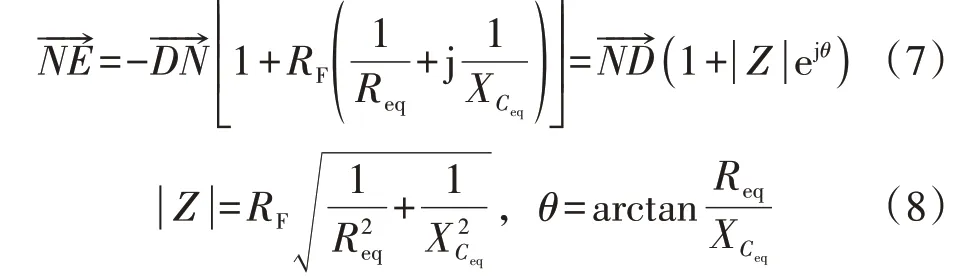
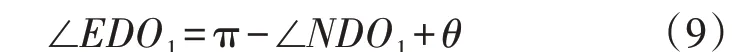
由于点N、E均在圆弧上，即||=||，根据正弦定理可得∠DEO1为：

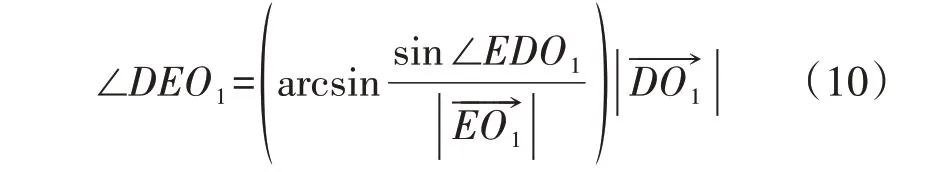
由上述步骤可得∠DO1E=π-∠EDO1，故障角γ=∠NO1D+∠DO1E，从而计算得到γ与β的比值，即为定子接地故障位置。

3）计算接地电阻。由γ可求得为：

A2 分支的定子接地故障位置及接地电阻计算方法以及其他相发生定子接地故障时的计算方法可参考上述步骤，在此不再赘述。

3 仿真分析

为验证理论分析的正确性，以A 电厂660 MW汽轮发电机参数为依据，搭建与实际参数相近的仿真系统进行试验验证，仿真模型如图5 所示，仿真模型的发电机、接地变压器参数如表1 所示。图5 中：Xe为发电机定子漏抗；模型采用多个电压源串联方式表征发电机定子绕组内部基波电势的分布特征，Ea101—Ea114、Ea201—Ea214分别为定子A1、A2 分支绕组内部基波电势，Eb101—Eb214、Ec101—Ec214分别为B相和C 相定子分支内部基波电势。由于每相定子绕组电阻和定子漏抗Xe与零序回路阻抗值相比小很多，在此忽略不计。根据式（2）、（3）分别计算得到Req=3 952.2 Ω、XCeq=4 395.6 Ω。对A 相定子绕组不同位置发生的接地故障进行仿真，为与常规方法进行对比，基于仿真所得数据分别采用式（4）所示的常规方法与本文方法进行计算。由于常规方法的计算完全依赖于准确的接地电阻值，需将已知的接地电阻值代入式（4），同时考虑引入注入式定子接地保护测量电阻正常工程误差范围±10%，故将90%RF与110%RF分别代入式（4）进行计算，得到常规方法的故障位置计算结果范围。下文详细介绍A 相定子绕组不同位置发生接地电阻为5 kΩ 的接地故障时的仿真和计算结果，更多的仿真和计算结果对比如附录A表A1所示。

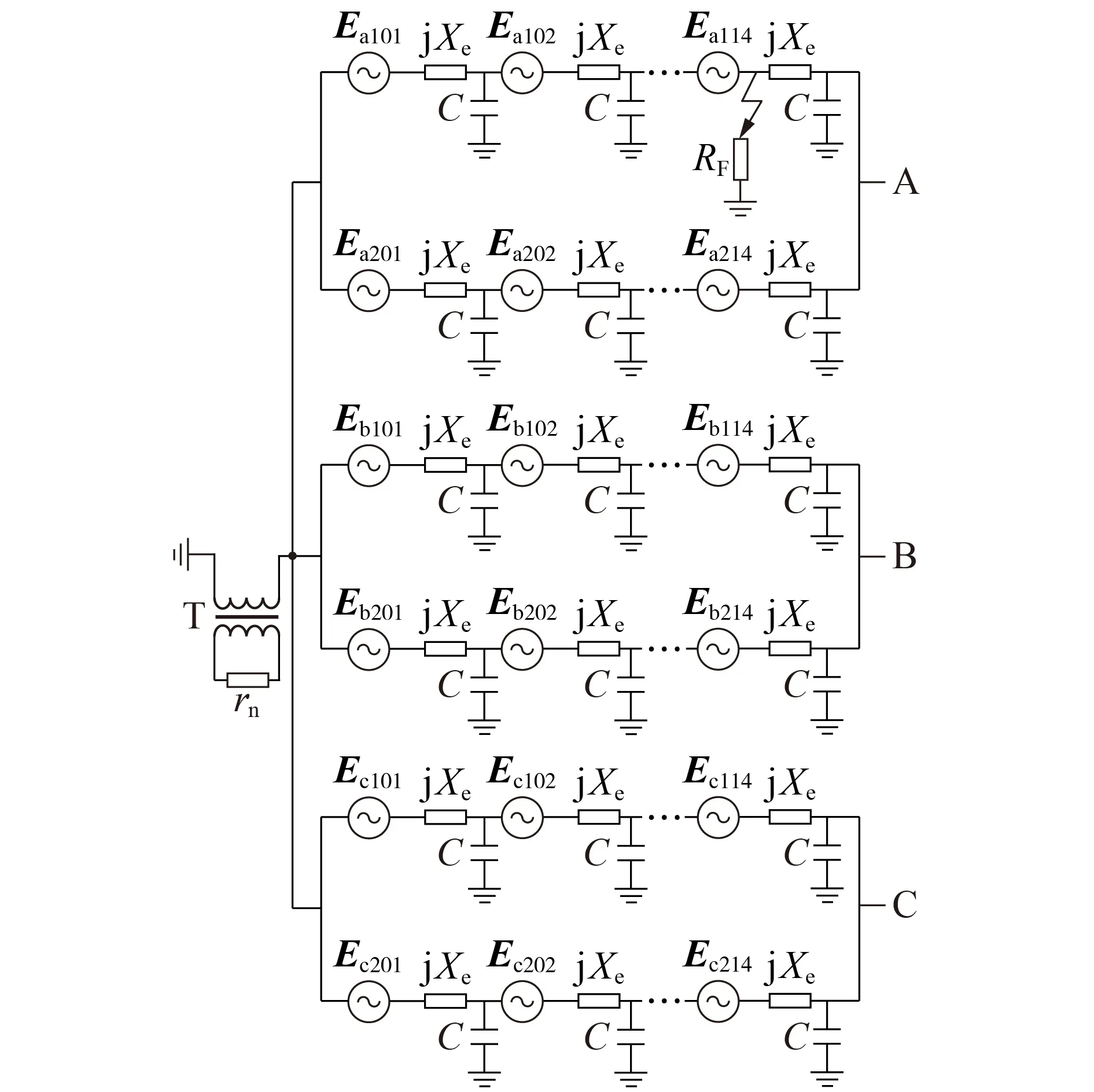
图5 A电厂660 MW汽轮发电机定子接地故障仿真模型Fig.5 Stator grounding fault simulation model of 660 MW turbo-generator in Power Plant A

表1 A电厂660 MW汽轮发电机及接地变压器仿真参数Table 1 Simulation parameters of 660 MW turbogenerator and ground transformer in Power Plant A

1）设置A 相定子绕组A1 分支2 号线棒（故障位置为14.28%）发生接地电阻为5 kΩ 的接地故障，仿真波形如图6 所示。图中，故障位置1—3 分别表示常规方法（110%RF）、常规方法（90%RF）和本文方法得到的故障位置，后同。由图6（b）可见：常规方法对应的故障位置1、2 分别为15.93%、13.99%，则常规方法相对理论值的误差范围为［-0.29%，1.65%］；本文方法对应的故障位置3 为14.28%，相应的接地电阻计算结果为4.990 kΩ。

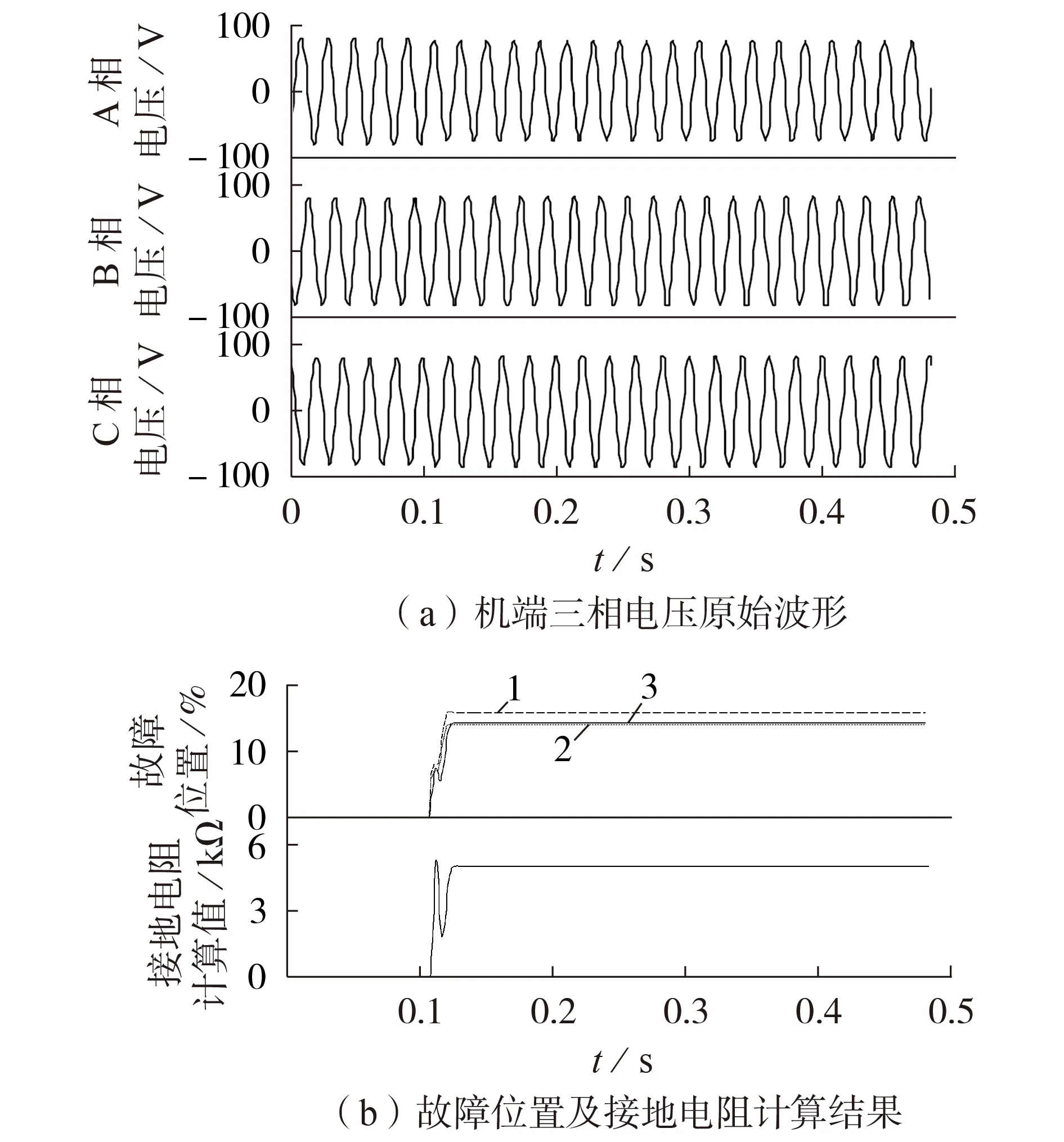
图6 A1分支2号线棒经5 kΩ电阻接地时的仿真波形Fig.6 Simulative waveforms when grounding fault with 5 kΩ grounding resistance occurs on branch A1 2th bar’s end

2）设置A1 分支6 号线棒（故障位置为42.85%）发生接地电阻为5 kΩ 的接地故障，仿真波形如图7 所示。由图7（b）可见：故障位置1、2 分别为47.42%、41.66%，则常规方法相对理论值的误差范围为［-1.19%，4.57%］；本文方法对应的故障位置3为42.84%，相应的接地电阻计算结果为4.992 kΩ。

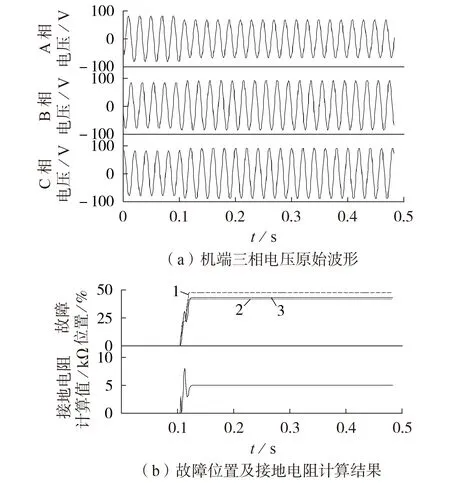
图7 A1分支6号线棒经5 kΩ电阻接地时的仿真波形Fig.7 Simulative waveforms when grounding fault with 5 kΩ grounding resistance occurs on branch A1 6th bar’s end

3）设置A1 分支9 号线棒（故障位置为64.28%）发生接地电阻为5 kΩ 的接地故障，仿真波形如图8所示。由图8（b）可见：常规方法对应的故障位置1、2 分别为69.52%、61.07%，则常规方法相对理论值的误差范围为［-3.11%，5.24%］；本文方法对应的故障位置3为68.03%，其相对理论值的误差为3.75%，这主要是因为本文所提方法中定子绕组内部基波电势为近似等效圆弧，与实际电势存在一定误差，导致计算结果存在一定偏差。

图8 A1分支9号线棒经5 kΩ电阻接地时的仿真波形Fig.8 Simulative waveforms when grounding fault with 5 kΩ grounding resistance occurs on branch A1 9th bar’s end

4）设置A2 分支14 号线棒（故障位置为100%）发生接地电阻为5 kΩ 的接地故障，仿真波形如图9 所示。由图9（b）可见：常规方法对应的故障位置1、2 分别106.6%、93.6%，则常规方法相对理论值的误差范围为［-6.4%，6.6%］；本文方法对应的故障位置3 为99.97%，相应的接地电阻计算结果为4.993 kΩ。

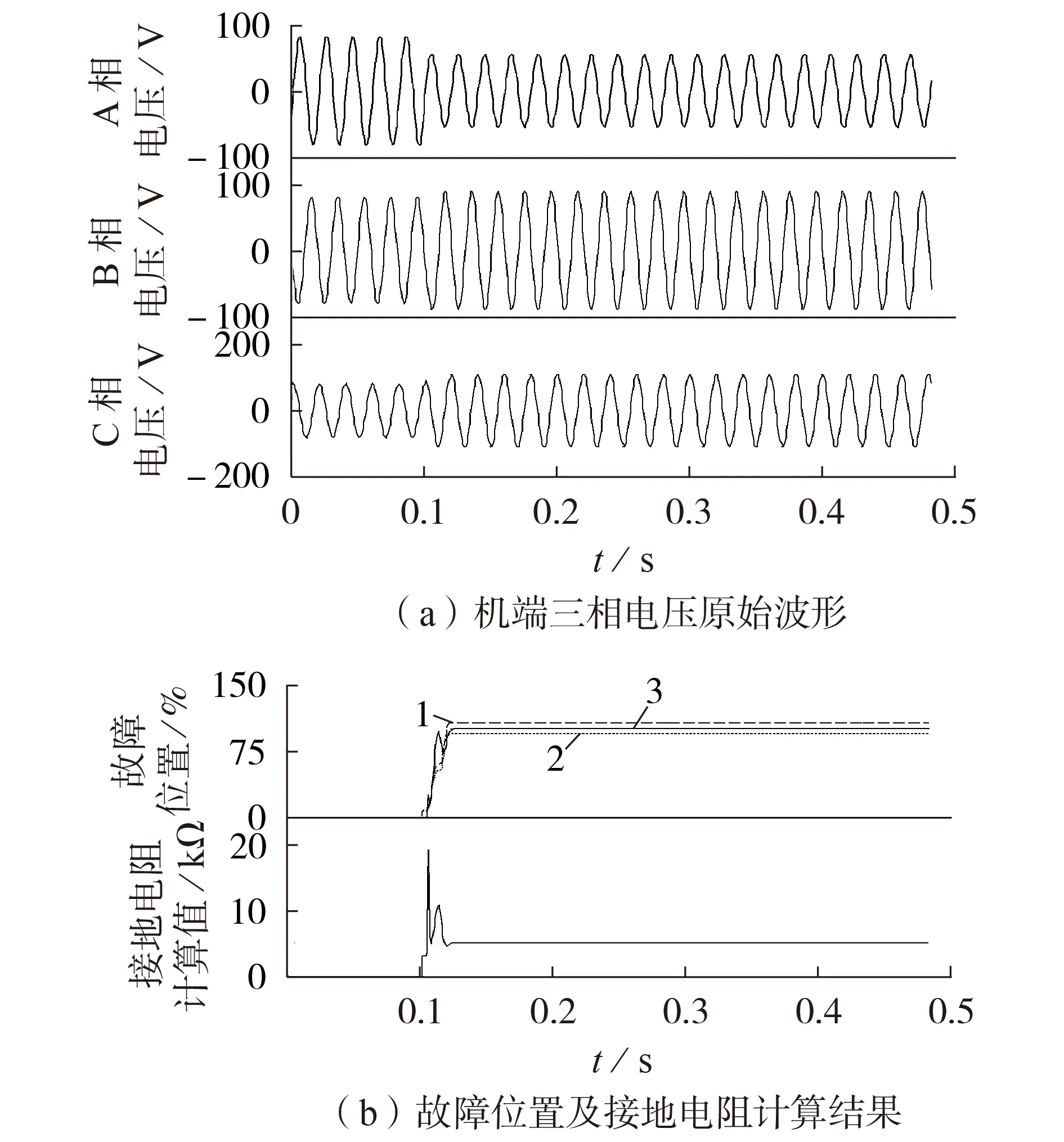
图9 A2分支14号线棒经5 kΩ电阻接地时的仿真波形Fig.9 Simulative waveforms when grounding faultwith 5 kΩ grounding resistance occurs on branch A2 14th bar’s end

通过上述仿真计算，常规方法在测量接地电阻值±10%工程误差范围内，计算结果与理论值存在一定的误差，这主要是由常规方法未考虑定子绕组基波电势分布特征与电阻值测量误差引起，若无法准确测量接地电阻则误差会更大。对于本文方法，其完全不依赖于接地电阻值，计算结果与理论值基本相吻合，虽然由于定子绕组内部基波电势为近似等效圆弧，与实际电势存在一定误差而导致在定子绕组某些位置会出现一定误差，但是若考虑进一步将模型等效细化，则可进一步提高精度。

4 现场案例分析

采用本文方法对多个汽轮发电机定子接地故障案例进行定位分析，接地位置计算结果与实际故障位置基本相符。以国内B 电厂660 MW 汽轮发电机发生的一起定子接地故障为例，介绍故障定位分析情况。该机组设备参数与第3 节的仿真模型参数一致，案例分析结果如图10 所示，发电机C 相电压最低可判定为故障相。由于发生故障时各相电压有所波动，本文方法计算的故障位置变化范围为［53.71%，73.15%］，接地电阻计算结果为5 kΩ 左右。根据现场排查结果，C相第15、16号线棒绝缘均有所下降，大致估算故障位置为［57.14%，71.42%］，则本文方法的计算结果与实际情况基本相吻合，验证了本文方法的正确性。

图10 B电厂发生发电机C相定子接地故障时的案例分析结果Fig.10 Case analysis results of phase-C generator stator grounding fault of Power Plant B

5 结论

本文分析了汽轮发电机定子接地故障下各电气量关系，考虑了定子绕组内部基波电势分布特征，通过建立定子绕组故障位置至中性点的基波电势与定子零序电压、机端绕组相电压等相量间的几何关系，结合零序回路阻抗特征参数，计算中性点至故障位置所对应的故障角，最终实现故障位置及接地电阻阻值的计算，并通过仿真试验及现场故障案例验证了可行性。本文方法简单有效，完全不依赖注入式定子接地保护，即可实现接地位置准确计算，且故障点靠近发电机中性点时精度也较高，能大幅提高发电机定子接地故障定位诊断精度与效率，缩短排查时间。

附录见本刊网络版（http：//www.epae.cn）。