基于振荡波多特征融合的变压器绕组故障诊断方法

周利军，周 猛，李沃阳，陈田东，吴振宇，王东阳

（西南交通大学 电气工程学院，四川 成都 611756）

0 引言

牵引变压器是高速铁路牵引供电系统的核心设备之一，其运行状态与轨道交通运行的安全稳定性密切相关［1⁃3］。根据国际大电网委员会的统计，绝缘破损和绕组变形是造成变压器损坏的常见故障，其中绕组变形故障约占26.6%［4］。变压器绕组变形在短路冲击力的作用下具有累积效性，会造成绕组屈曲、绕组移位、短路等故障，甚至会造成安全事故。因此，有效诊断变压器绕组状态，从而为变压器检修提供参考，对牵引供电系统的安全可靠运行具有重大意义［5］。

目前，国内外学者陆续提出了多种变压器绕组状态检测方法，例如测量绕组等效阻抗的短路阻抗法［6］、监测变压器箱壁振动信号的振动法［7］以及通过变压器绕组网络响应特性判断绕组变化情况的频率响应法FRA（Frequency Response Analysis）［8⁃10］。其中，短路阻抗法能够简单直观地反映绕组的状态，但其能够诊断的信息较为有限，对于绕组的故障类型、故障位置等较难作进一步的深入分析；振动法能够实现变压器状态在线监测，不干扰牵引供电系统的正常运行，但传感器的布置、变压器运行环境等在一定程度上会影响信号的采集和分析；相比于其他方法，基于FRA 的绕组状态检测技术发展较为成熟，国内外已形成相关标准，其通过幅频曲线在低、中、高3 个频段的相似系数综合判断绕组的故障程度。为了进一步提高FRA 故障诊断的准确性，学者们提出了多种维度提取特征参数的方法，例如极坐标图［8］、二值化图像［9］、传递函数［10］方法等。上述研究工作为实现变压器绕组变形的有效检测做出了重要的贡献。

为了进一步提高绕组变形检测的效率，近年来学者们提出了一种基于开关过电压和脉冲频率响应的振荡波法［11⁃14］，该方法不仅能够反映绕组状态变化，而且易实现高压等级测试，拥有较强的抗干扰能力，是现有检测方法的一种有效补充。已有研究建立220 kV 变压器试验平台，开展高压振荡波试验，试验结果表明：振荡波法抗干扰能力强、测试重复性高。在此基础上探究了不同电源参数下振荡波的演变规律，明确了该检测方法下的最优测试技术［11⁃12］。基于有限元仿真建模开展了不同绕组状态下等效电路参数与振荡波变化规律的关联性研究，同时搭建绕组故障模拟平台，验证了该方法对绕组故障的高灵敏性［13⁃14］。但针对振荡波特征提取及故障诊断的系统研究尚未开展。

为此，本文针对变压器绕组的振荡波信号特征提取以及故障诊断方法进行研究与讨论。首先基于振荡波曲线特点提取波形特征；然后通过小波包变换将振荡波转化为时频图，提取颜色矩特征和颜色聚合向量CCV（Colour Coherence Vector）特征；结合故障属性相关特征，通过多特征融合进行绕组故障类型、故障程度以及故障位置的识别；最后在一台等比例牵引变压器模型上模拟轴向移位故障、饼间电容故障以及饼间短路故障，使用提出的多特征融合方法进行分析，并通过粒子群优化-支持向量机PSO-SVM（Particle Swarm Optimization-Support Vec⁃tor Machine）算法识别绕组故障验证了方法的可行性。本文所提方法可为进一步的牵引变压器绕组故障诊断提供参考。

1 振荡波原理

当频率大于1 kHz 时变压器绕组可视为由电阻、电容、电感等分布参数构成的无源非线性电路网络，如附录A 图A1所示。振荡波法是在绕组一端连接高压直流电源对系统进行充放电，在绕组间电容电感效应下电荷无法立即储存或释放，可在绕组另一端获取振荡波信号［11⁃12］。

振荡波测试原理图如图A1 所示。图中高压直流电源电源系统由高压电容、高压直流电源、限流电阻以及绝缘栅双极型晶体管IGBT（Insulated Gate Bipolar Transistor）高频开关组成，具体的充电和放电过程如下［13⁃14］。

1）充电过程：IGBT 高频开关断开，高压直流电源通过高压电容与绕组形成充电回路产生振荡波，一旦充满电，采集端电压就会稳定。

2）放电过程：IGBT高频开关接通，高压直流电源和限流电阻对地短路；高压电容的一个端口直接接地，与电源形成直流回路，另一个端口与变压器绕组串联形成放电回路产生振荡波。根据IEC 60071-2标准可知，相同激励下的暂态响应（即振荡波）与变压器绕组自身属性相关［15］，因此，振荡波可用于变压器绕组的故障诊断。

现场试验所得振荡波如图1所示。由图可见，变压器在周期性的充放电过程中会产生规律性的振荡波，充电与放电过程中的振荡波形具有良好的对称性。本文只针对放电过程的振荡波信号开展研究。

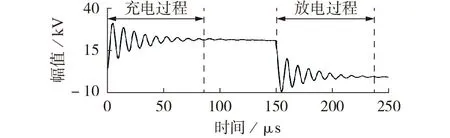
图1 现场试验所得振荡波Fig.1 Oscillating waves of field test

2 多特征融合故障诊断方法

振荡波法是一种比较方法，其利用不同状态下振荡波特征的变化作为故障诊断的依据，为了消除电压等级影响，根据式（1）对振荡波进行归一化处理。

式中：xstd为归一化处理后的振荡波信号；X为测试的振荡波信号；U为电源幅值。

2.1 波形特征

波形特征能够准确描述振荡波曲线特征［16］，如谐振点的振幅、波形形状等，可以有效提取振荡波信息。

1）峰峰值。

峰峰值Vpk是振荡波信号最高值和最低值的差值，它描述了振荡波谐振点振荡的变化范围，具体如式（2）所示。

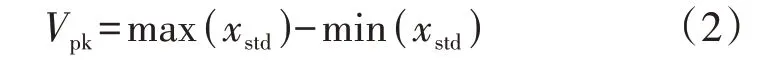
2）峰值因子。

峰值因子VC是振荡波信号峰峰值与有效值的比值，它描述了振荡波振幅在波形中的极端程度，具体如式（3）所示。

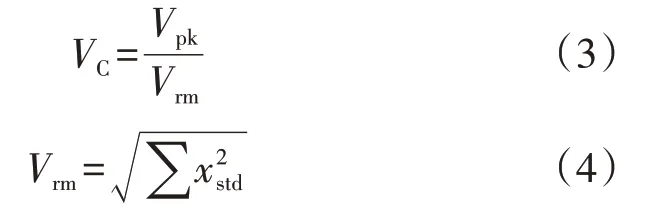
式中：Vrm为振荡波的有效值。

3）波形因子。

波形因子VS是有效值与平均值的比值，它描述的是振荡波整体幅值的变化情况，具体如式（5）所示。

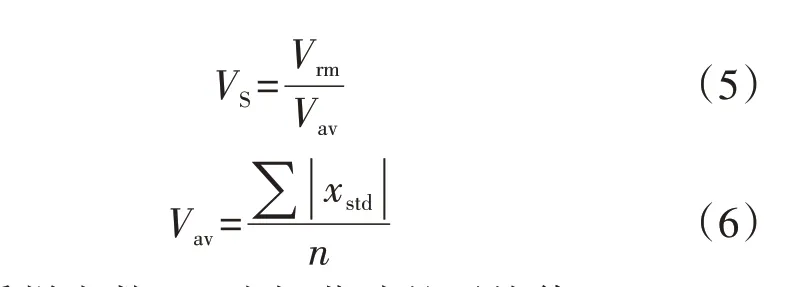
式中：n为采样点数；Vav为振荡波的平均值。

2.2 颜色特征

振荡波是一种非平稳暂态信号，当变压器绕组的故障程度或故障位置发生改变时，振荡波不仅时域波形发生改变，频域信息也会发生相应的变化，联合时域和频域2 个维度进行分析，可以进一步提取振荡波的有效特征。

小波包变换是一种精细、灵活的信号分析技术，可以同时对信号的低频部分和高频部分进行分解，拥有良好的时频分析能力，能够有效提取非平稳暂态信号的时频特征［17］。绕组正常情况下的小波包时频图见附录A 图A2，振荡波信号各频带的能量分布情况可通过颜色的深浅反映，且随着频率的升高，各频段的颜色变化逐渐强烈，能够反映振荡波时频信息。

小波包时频图体现为颜色深浅以及颜色分布情况，由图像颜色特征能有效提取小波包时频图信息。颜色特征的优势在于对图像尺寸、方向以及视角的依赖性较弱，具有较高的稳定性，常用的颜色特征有颜色矩、颜色聚合向量特征［18⁃19］。

颜色矩能够全面描述图像的整体信息，图像颜色信息主要集中在一阶矩、二阶矩和三阶矩，一阶矩描述颜色平均程度，二阶矩描述颜色方差，三阶矩描述颜色偏斜度［18］。

综合图像3 个颜色通道的颜色矩定义特征参数Ci如式（7）—（9）所示。

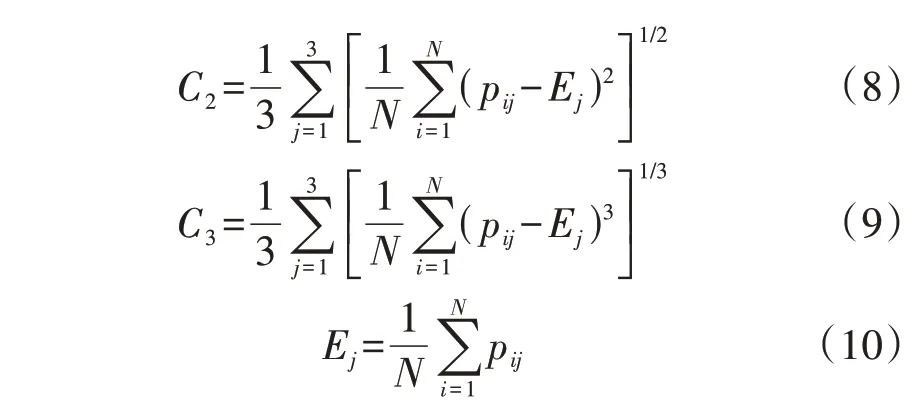
式中：pij为第j种颜色分量的第i个像素值；N为图像总像素数；Ej为第j种颜色分量的像素平均值。

颜色聚合向量根据像素间的连通性划分连通区域，然后通过比较每个独立的连通区域总像素数与定义阈值划分聚合和非聚合像素，从而构建聚合向量，具体计算步骤如下［19］。

1）量化：针对任一颜色分量均匀量化为k个颜色区间，得到k级颜色像素值矩阵。

2）划分连通区域：将重新量化的颜色像素值矩阵根据像素间的连通性划分成若干个连通区域，即如果一个区域C 中所有像素的量化值相等，且区域C 中任意2 个像素点P和P'之间都存在1 条通路，则称C为连通区域。

3）判断聚合性：将颜色像素矩阵划分为多个连通区域，统计每个独立的连通区域C中的像素数NC，根据阈值ε（ε一般为1%N）判断连通区域C 中像素的聚合性，具体如式（11）所示。

4）聚合向量：根据上述判断依据统计各连通区域中的聚合像素D和非聚合像素W，则该颜色分量的C可以表示为＜（D1，W1），（D2，W2），…，（Dk，Wk）>。

5）特征参数：对图像的多个颜色分量进行颜色聚合向量计算，定义距离参数Dstd和Wstd表示不同图像的颜色聚合向量之间的差异，即：

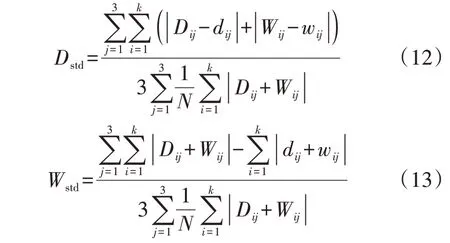
式中：dij为参考图像第j个颜色分量第i级的聚合像素；Dij为比较图像第j个颜色分量第i级的聚合像素；wij为参考图像第j个颜色分量第i级的非聚合像素；Wij为比较图像第j个颜色分量第i级的非聚合像素。

2.3 故障诊断方法

本文为实现变压器绕组故障类型、故障程度以及故障位置的识别，采用多特征融合的方法进行绕组故障诊断。

变压器绕组发生故障时等效电气参数会发生改变，在振荡波信号中体现为波形的相应移动，例如谐振点偏移、振荡幅值变化等。不同故障影响下的等效电气参数变化趋势不同，使得各故障下振荡波波形差异明显，而波形特征能够准确描述曲线形状，因此本文选择波形特征分辨绕组故障类型。

振荡波随着绕组故障程度的加深呈现规律性偏移［13］，在小波包时频图中表现为颜色的整体变化。颜色矩的计算无需对颜色进行量化处理，保证了图像颜色的完整性，从而能够描述图像颜色整体分布情况［18］，因此本文选择颜色矩特征区分绕组故障程度。

变压器绕组的不同位置发生故障时，在小波包时频图中表现为颜色分布位置的改变。颜色聚合向量根据连通区域的划分以及聚合性的判断，能够描述图像颜色分布的空间信息［19］，因此本文选择颜色聚合向量特征识别绕组故障位置。

综上所述，波形特征、颜色矩特征和颜色聚合向量特征分别能够反映绕组故障类型、故障程度和故障位置的信息变化情况，基于振荡波多特征融合的绕组故障诊断流程如图2所示，具体步骤如下：

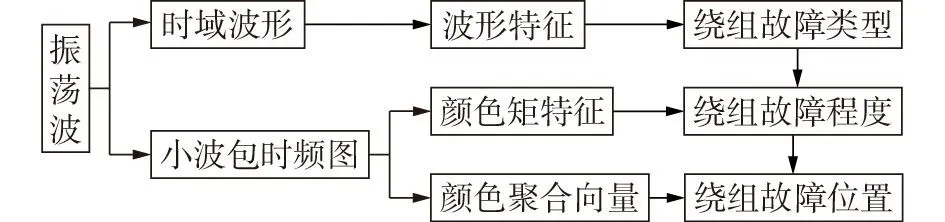
图2 故障诊断流程图Fig.2 Flowchart of fault diagnosis

1）根据振荡波曲线提取波形特征峰峰值、峰值因子和波形因子识别绕组故障类型；

2）根据振荡波小波包时频图提取颜色矩特征Ci识别绕组故障程度；

3）根据振荡波小波包时频图提取颜色聚合向量特征Dstd和Wstd识别绕组的故障位置。

为验证本文所提方法用于变压器绕组故障诊断的有效性，选择识别精度高的PSO-SVM 算法对算法的每一步骤进行智能识别［20］。

3 试验平台

3.1 试验平台搭建

本文搭建了等比例牵引变压器绕组模拟平台，如附录A 图A3 所示。该绕组结构为牵引变压器结构，每相铁芯的芯柱为三绕组结构，铁芯的直径和高度分别为53、530 mm。从铁芯向外分别为牵引绕组（T）、馈电绕组（F）和高压绕组（HV）。试验变压器的各绕组均为18个双饼，每饼匝数为32匝，线饼高度为20 mm。双饼两端采用铜鼻子焊接，饼与饼之间通过高导电黄铜螺母连接以实现不同绕组故障的模拟。

为了验证本文所提变压器绕组故障诊断方法的有效性，针对牵引绕组HV 轴向移位故障、饼间电容故障和饼间短路故障和进行模拟，试验变压器绕组故障设置如附录A图A4所示。

1）轴向移位故障通过在饼间增加一定数量的垫块实现，轴向移位故障程度Δ如式（14）所示［21］。

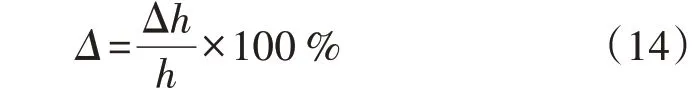
式中：Δh为轴向移位高度；h为绕组总高度，约为450 mm。

垫块厚度约为1.5 mm，模拟1%轴向移位故障需在饼间添加3 个垫块。绕组从顶部到底部的各饼序号分别为1—18，在18 个位置均模拟了故障程度为1%、2%、…、7%的轴向移位故障，共进行126 组试验。

2）变压器绕组发生饼间间距变化、鼓包等故障会引起饼间纵向等值电容变大［22］，可通过在变压器模型的饼间并联电容进行模拟。根据文献［23］提供的解析式计算饼间电容正常值，选取100、150、200、250、300 pF 的电容值模拟饼间间距、屈曲等故障的不同变化程度，共进行90组试验。

3）饼间短路故障通过短接线连接对应饼的铜鼻子接头实现，每种饼间短路故障重复试验5 次，共进行90组试验。

本文将对绕组故障程度以及故障类型开展分析，因此将绕组故障位置分为上端（1—9 饼）和下端（10—18饼）这两部分，将轴向移位故障程度分为轻微（移位1%、2%）、中度（移位3%、5%）和严重（移位6%、7%），将饼间电容故障程度分为轻微（并联电容为100、150 pF）、中度（并联电容为200、250 pF）和严重（并联电容为300 pF）。

3.2 数据解析

基于搭建的变压器绕组故障模拟平台开展振荡波试验，振荡波电源系统参数如下：充电电压为10 V，充电时间为100 μs，开关时间为1 μs，高压电容为2.2 μF。振荡波测试结果如附录A 图A5 所示，图中标记1—3 分别代表故障发生在绕组第1、9 和18 饼。与绕组正常状态下的振荡波形相比，3 种绕组故障下的振荡波形有着明显的变化，且变化趋势不一致：饼间短路故障的振荡波中后部分幅值的变化显著，波形轻微地向左偏移；饼间电容故障体现为波形向右偏移以及幅值的降低，轴向移位故障表现为谐振点从向左偏移逐渐变为向右偏移，同时幅值也有略微降低。由上述分析可以看到绕组在不同故障下的振荡波变化差异性较大，说明振荡波波信号对绕组状态有较高的灵敏性，可通过波形特征进一步描述故障类型。

3 种变压器绕组故障的小波包时频图见附录A图A6，图中红色虚线框内为各故障下的主要变化区域。由图可见：发生饼间电容故障时，在小波包时频图中主要体现为高频段颜色变浅以及能量分布改变；发生轴向移位故障时，小波包时频图集中在低频段发生改变；发生饼间短路故障时，小波包时频图的低频段能量分布变化明显，同时高频段也有一定程度的变化。小波包时频图能较好地描述绕组状态变化，可根据图像进一步提取特征对变压器绕组故障程度、故障位置进行分析。

4 试验结果分析

为了比较绕组在正常和故障状态下的差异性，按照式（15）处理波形特征和颜色矩特征。

式中：Ff、Fh分别为绕组在故障、正常状态下的特征值。

4.1 故障分类

由图A5可以看出，不同故障类型的时域振荡波曲线形状区别明显，通过波形特征可以有效识别绕组故障类型，绕组故障类型特征分类图如附录A 图A7 所示。由图可见，饼间短路故障与其他故障差别明显，饼间短路故障的峰峰值和峰值因子最小值分别为1.54 和1.52，波形因子最大值为1.01，其他故障的峰峰值小于0.92，峰值因子小于1.46，波形因子大于1.20。

根据故障波形特征分析可知，3 种故障在波形特征的三维分布空间具有聚类和分类特性，饼间短路故障属于严重故障，与其他故障区分度明显，轴向移位和饼间电容故障在单一特征值的分布区域具有一定重叠，需通过3 种波形特征所表征的空间位置进行区分。

4.2 故障程度

基于颜色矩特征分析绕组故障程度，结果如附录A图A8所示，具体分析如下。

1）轴向移位故障程度：轻微故障下C1的最大值为-0.02，其他故障程度下C1≥0；中度故障下C1的最小值为0.01，C3的最小值为-0.19；严重故障下C3的最大值为-0.23，其他故障程度下C3≥-0.20。

2）饼间电容故障程度：轻微故障下C1的最大值为0.71，其他故障程度下C1≥0.72；中度故障下C2的最小值为0.44，其他故障程度下C2≤0.43；严重故障下C3的最大值为0.46，其他故障程度下C3>0.46。

根据以上分析可知，不同故障程度的颜色矩特征在三维空间的分布呈现聚类性和一定的分离性，绕组故障程度区分的初步界限如表1 所示。由表可见：轴向移位故障的轻微、严重故障程度可分别通过C1、C3识别，中度轴向移位故障可结合C1和C3与其他故障程度进行区分；饼间电容故障的轻微、中度、严重故障程度可分别通过C1—C3进行识别。

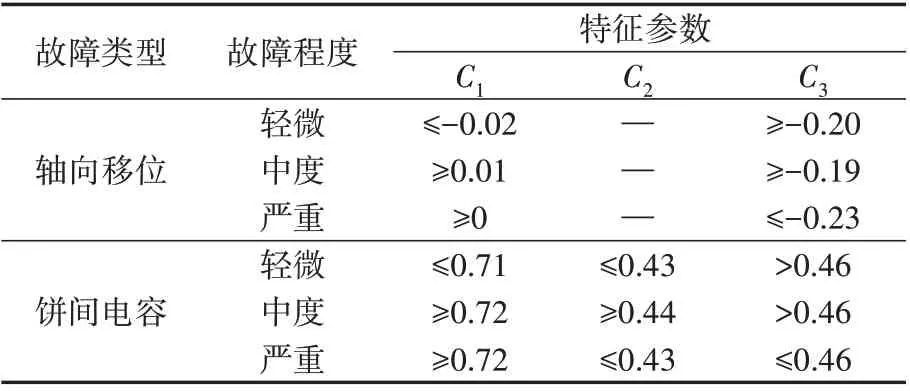
表1 故障程度界限表Table 1 Threshold of fault degrees

4.3 故障定位

基于颜色聚合向量分析绕组故障位置，结果如图3 所示。由图可见：饼间短路故障发生在上端时Wstd>0.6，发生在下端时Wstd＜0.4；饼间电容故障以Wstd=0.4 为分界线，轴向移位故障以Dstd=-0.02 为分界线，从而由颜色聚合向量可识别大部分绕组故障位置。

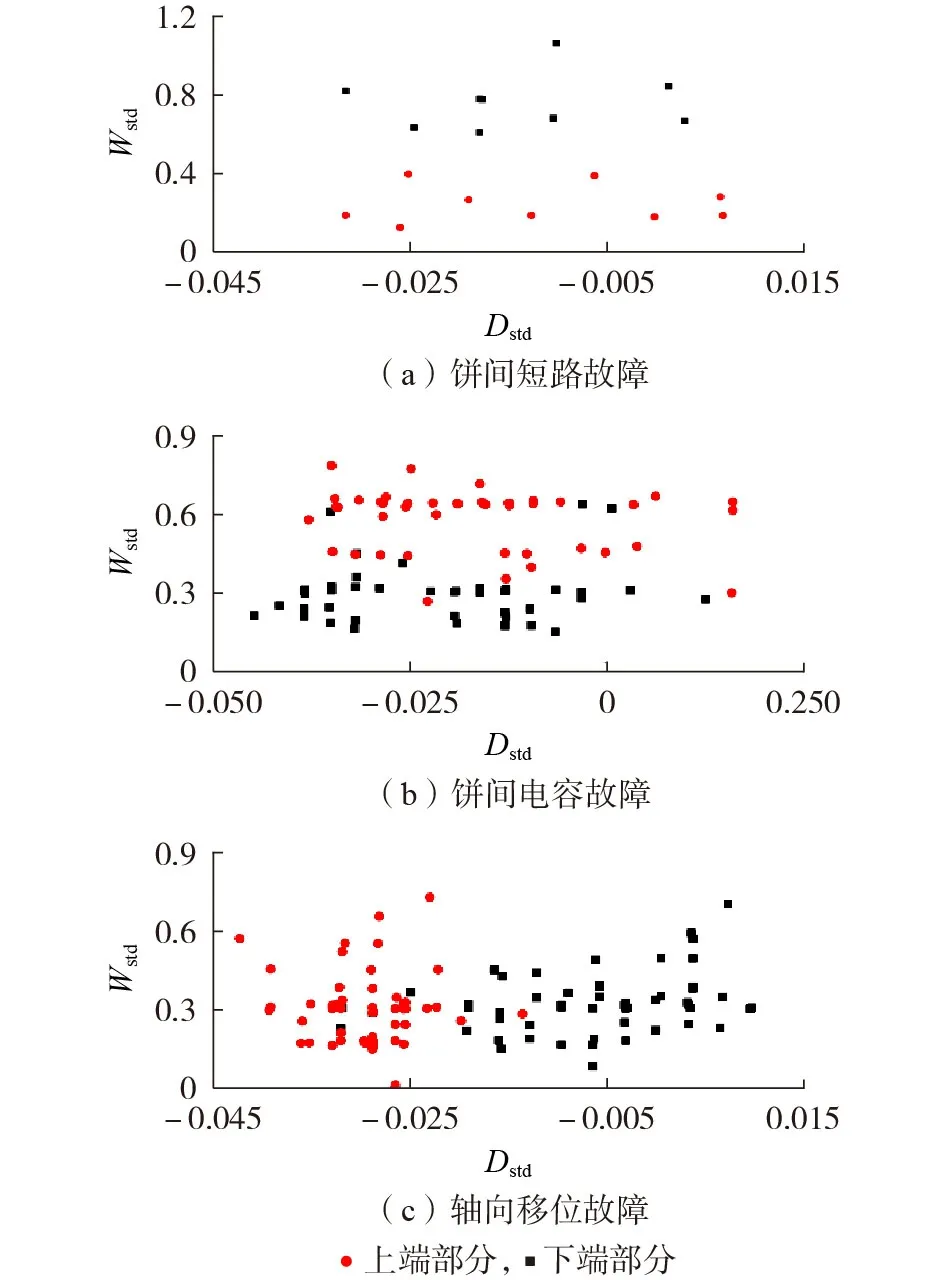
图3 绕组故障位置特征分析Fig.3 Characteristic analysis of winding fault position

根据上述分析可知：不同故障位置的颜色聚合向量特征的分布都具有可分离性，通过Wstd可识别饼间短路和饼间电容故障位置，轴向移位故障位置则通过Dstd进行识别；饼间电容和轴向移位故障对绕组等效参数的影响有限，不同故障位置的分布有一定的重叠。

4.4 故障诊断

根据以上分析，本文所提取的振荡波特征对绕组故障类型、位置、程度都表现出良好的识别性。将试验模拟的306个案例通过PSO-SVM 算法进行故障诊断，训练集和测试集的比例为3∶1，故障识别率取5次故障诊断的平均值，如表2所示，由表可见，绕组故障类型、故障程度、故障位置的识别率均在95%以上。

表2 故障诊断结果Table 2 Results of fault diagnosis

本文所提方法可有效识别变压器绕组故障类型、故障程度、故障位置，为牵引变压器绕组故障检测提供参考。

5 结论

本文提出了一种基于振荡波多特征融合的变压器绕组故障诊断方法，该方法综合了振荡波的时域波形特征和小波包时频图颜色特征，提升了故障诊断的灵敏度，最后搭建变压器平台对所提方法进行试验验证，所得结论如下。

1）轴向移位、饼间电容和饼间短路3 种绕组故障下的振荡波时域波形相比健康绕组的振荡波时域波形呈现出一定的变化规律，轴向移位故障引起波形轻微偏移、幅值小幅下降，饼间电容故障引起波形整体向右下偏移，饼间短路故障使波形出现明显偏移、幅值的变化显著，因此通过波形特征的数值变化可以反映绕组故障类型。

2）3 种绕组下，故障振荡波小波包时频图呈现出差异性，轴向移位故障下小波包时频图以低频段变化为主，饼间电容故障下小波包时频图主要体现为高频段变化，而饼间短路故障下小波包时频图在全频段变化明显，颜色矩和颜色聚合向量特征分别反映了绕组的故障程度与故障类型。

3）波形特征、颜色聚合向量、颜色矩分别针对故障类型、故障程度、故障位置的空间分布具有分离和聚类特性，基于PSO-SVM 算法的绕组故障诊断准确率都在95%以上。

附录见本刊网络版（http：//www.epae.cn）。