分布函数差异化导向的风电功率预测误差气象条件概率建模方法

刘念璋，杨 健，柳 玉，姜尚光，柯德平，孙元章

（1. 武汉大学 电气与自动化学院，湖北 武汉 430072；2. 国家电网有限公司华北分部，北京 100000）

0 引言

随着风电渗透率的不断提高，风电的随机波动性给电力系统的安全、稳定和经济运行带来了巨大的挑战。高精度的风电功率预测对于电力系统的调度控制、安全防御等具有重要的意义与价值［1］。然而，现有的风电功率预测方法不可避免地存在预测误差［2］，较大的预测误差会导致电力系统出现弃风、切负荷等现象。

近年来，国内外对风电功率预测误差的常用处理方法是对其进行统计特性建模，将所得模型的结果叠加到风电功率预测值上，从而获得风电功率概率分布信息，并将其应用于考虑风电不确定性的随机经济调度计算中［3⁃4］。建模过程通常为条件概率分布建模：文献［5］利用经验累积分布函数和非参数回归方法建立各风电功率预测区间的预测误差概率分布模型；文献［6］通过对各功率预测区间的预测误差进行统计分析，利用通用分布模型对其进行建模；文献［7］利用蒙特卡罗双层抽样技术和最大似然估计法建立各风速区间的风速-风电功率联合条件概率分布模型；文献［8］按照风速对历史误差进行聚类，并利用经验分布建立不同风况下的误差概率分布模型。然而，从统计原理角度看，上述文献均未说明预测误差的条件概率模型相较于简单的预测误差频次模型的优势。

事实上，风电的随机波动性是各种复杂天气因素共同作用的结果，预测方法的预测误差与各气象因素密切相关［9⁃10］，因此，可以建立以气象信息为依据的风电功率预测误差条件概率分布［11］，即对气象数据进行分类并建立各类气象数据对应的风电功率预测误差数据的概率模型。值得一提的是，上述风电功率预测误差先验概率知识（即不同气象数据类别对应不同的预测误差概率分布）要能从统计学角度保障其应用价值。

针对风电功率短期预测误差，本文提出一种分布函数差异化导向的气象条件概率建模方法。将历史气象数据聚合成多个类别（气象模式），并建立对应的风电功率预测误差的条件概率模型，该模型可应用于日前随机经济调度中。与现有气象模式分类方法相比，本文方法的主要创新点在于，在气象数据的聚类过程中考虑对应预测误差分布函数的差异性，保证得到的预测误差条件概率模型在应用于随机经济调度时可以取得比简单的预测误差频次模型更好的决策结果，即从统计学角度提升电网的风电消纳水平。

1 风电功率预测误差（气象）条件概率建模的基本思路

从概率论角度而言，应用了更多经验的贝叶斯推理一般要优于简单的频次推理，即相较于风电功率预测误差频次模型，以气象信息为推理依据的风电功率预测误差条件概率模型通常更加有利于解决随机调度决策问题。本文建立风电功率预测误差（气象）条件概率模型的基本思路如下。

1）基于某风电场同一采样时刻的多维历史气象数据（风速、气温、气压等）和历史风电功率预测误差数据（最长提前预测时间为24 h），将历史气象数据进行分类，将每类相似气象样本构成的气象数据集称为一个气象模式，拟合每类气象数据对应的历史风电功率预测误差数据的分布函数，并将其称为风电场这类气象数据或这个气象模式对应的风电功率预测误差条件概率模型。

2）对于数值天气预报NWP（Numerical Weather Prediction）在日前给出的未来某时刻的气象预测结果，通过模式识别将其归属于某个气象模式，并将该气象模式对应的风电功率预测误差概率密度函数PDF（Probability Density Function）作为该时刻的风电功率预测误差条件概率模型。同时，将该条件概率模型的结果与该时刻风电功率预测值相叠加，从而得到该时刻风电场的风电功率分布函数模型。

具体建模流程图如附录A 图A1 所示。不难看出，以气象信息为依据的预测误差条件概率模型在应用于解决随机调度决策问题时的一个关键之处在于气象模式分类提供了有效的先验统计信息。若不考虑气象先验统计信息的有效性，则可能导致所得的不同气象条件对应的预测误差气象条件概率模型间无明显区别，这会使得预测误差气象条件概率建模的思路不会为解决随机调度决策问题提供实质性帮助。举例说明如附录B所示。

基于上述分析，本文提出风电功率预测误差分布函数差异化导向的气象数据模式分类方法，以使得分类后各气象模式对应的预测误差概率密度函数存在明显的差异性，即保证先验的气象模式分类信息对于解决随机调度决策问题是有效的。此外，如同一般的分类问题，分类后的气象数据需要具有良好的聚合特性（即分类边界明显）。图1 为上述分类方法的效果图，图中灰度反映气象样本密集程度。由图可见，在保证分类后气象数据良好的聚合效果下，各模式的风电功率预测误差分布具有明显的差异性，如模式Ⅰ下多数为具有较小预测误差的点，而模式Ⅲ下则相反。

图1 分布函数差异化导向的气象数据模式分类Fig.1 Classification of weather data modes based on differentiation orientation of distribution function

2 预测误差分布函数差异化导向的气象模式聚类与识别

本文选择风电场风机轮毂处的风速、风向、气温和气压构成多维气象向量，利用改进的K-means 算法对该气象向量的历史数据进行聚类，同时，对于NWP 给出的未来某时刻该气象向量的预测值，采用支持向量机SVM（Support Vector Machine）算法对其进行分类识别。考虑到不同季节间气象的差异，对历史数据按季节分箱后得到各季度历史数据子集，再采用该算法进行分类识别，以提高建模精度。

2.1 改进的K-means算法

2.1.1 分布函数差异化导向

传统聚类算法（如K-means 算法）多是以样本自身间的距离作为相似性度量［12］，若将其应用于本文中的气象数据聚类分析，则聚类过程仅涉及气象数据，而不能考虑聚类后各气象模式下的预测误差概率分布特性。如前所述，若各气象模式间的预测误差概率分布差异不大，则气象模式-误差分布的先验信息对解决随机调度决策问题没有实质性帮助。为此，本文以预测误差分布函数差异化为导向，在聚类时引入均方根误差RMSE（Root Mean Squared Error）作为两概率分布间的相似度指标，如式（1）所示。

式中：eRMSE为RMSE；L1、L2为2 个气象模式对应的预测误差概率密度函数曲线，可以分别由这2 个气象模式对应的历史预测误差数据集ΔP1、ΔP2拟合计算得到（如采用MATLAB中的核密度估计函数ksdensi⁃ty）；L1，i、L2，i为两曲线上对应的第i个相同预测误差值的概率密度值；s为采样点数。eRMSE越小，则两概率密度曲线间的相似度越高。

为表征某一聚类结果下各气象模式之间风电功率预测误差概率分布的总体差异程度，本文提出指标累积均方根误差SRMSE（Sum of Root Mean Squared Error），如式（2）所示。

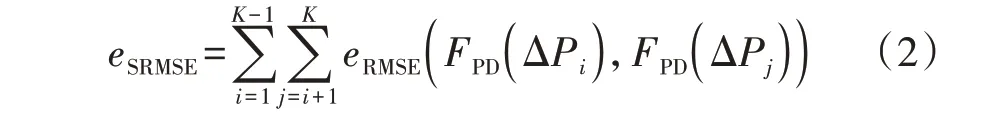
式中：eSRMSE为SRMSE；K为气象模式数；FPD(⋅)为概率密度函数。eSRMSE表征了各气象模式下预测误差概率密度函数曲线间的总体差异程度。本文将SRMSE 最大化作为聚类目标函数，以保证最终聚类结果下各气象模式间的预测误差概率分布有明显区别。

从基本的应用逻辑上而言，一种成熟的商用预测软件（方法）应在多数天气条件下能给出较好的预测结果。过多地聚焦于分布函数间差异的最大化将可能导致分布函数先验信息有效性与合理性之间的失衡，因此，聚类过程还应对聚类结果的合理性进行判断。由图2 中的预测误差概率密度函数曲线可见：高精度的预测误差概率密度函数曲线呈现高窄的形状且函数值集中在0 附近，而低精度的预测误差概率密度函数曲线则较扁平。因此，本文利用反映概率密度函数曲线陡峭程度的峰度系数Kurtosis来衡量各气象模式下预测误差概率密度函数曲线对应的精度水平，如式（3）所示。

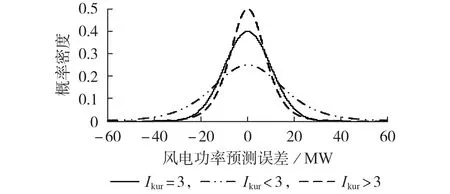
图2 预测误差概率密度函数曲线及其峰度系数Fig.2 PDF curves of forecasting error and corresponding Kurtosis

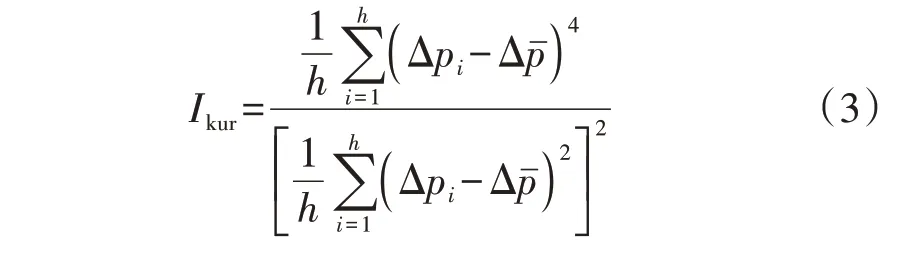
式中：Ikur为计算出的峰度系数Kurtosis；Δpi为某气象模式下预测误差数据集中的第i个样本；Δpˉ为该模式下所有预测误差的均值；h为该模式下预测误差的样本数。本文以3 作为峰度系数Kurtosis 的基准值，定义指标Nkur，表示预测误差概率密度函数曲线的Ikur>3 的气象模式对应样本数之和与总样本数之比，如式（4）所示。

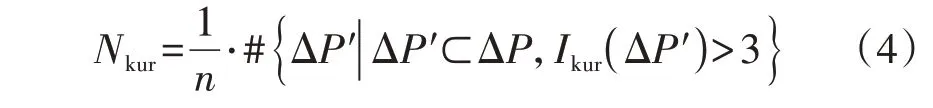
式中：“#”表示对集合中样本进行计数；ΔP为总预测误差数据集；n为ΔP中的样本数；ΔP'为预测误差概率密度函数曲线的Ikur>3 的气象模式对应的预测误差数据集。如果预测误差概率密度函数曲线呈明显的多峰或厚尾分布［13］，则仅以Ikur>3 进行判断可能不够充分，此时可基于标准GB／T 40607—2021《调度侧风电或光伏功率预测系统技术要求》［14］中对风电场短期预测的准确率大于83%的要求进行二次判断来获取指标Nkur。本文中，当Nkur>60%时，认为聚类结果满足预测精度水平较高的气象模式对应的样本占多数的统计特性要求。

2.1.2 聚类参数的选取

在K-means 算法中，聚类数与初始聚类中心的选取会对聚类效果产生直接影响。本文采用肘部法来确定聚类数K，并基于数据密度形成初始聚类中心候选集Wo。

肘部法的原理［15］是在K取不同值时对样本进行K-means 算法计算，随着K的不断增大，样本的误差平方和SSE（Sum of Squared Error）会不断减小，而其减小速率会在理想聚类数处骤减，如附录A 图A2所示，因此，根据SSE-K关系曲线的肘部即可确定理想聚类数。

对于气象数据集W={w1，w2，…，wi，…，wn}，其元素wi为某采样时刻的多维气象向量，则wi的数据密度Ndens(wi)可用以wi为中心、r为半径的球体内所包含的其余样本数来表示，如式（5）所示。

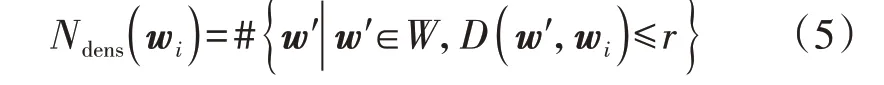
式中：D(w'，wi)为样本w'与wi之间的距离，w'表示W中与wi的距离小于r的样本。

通过设置合理的半径r，选取数据密度大于密度阈值μ的样本点形成初始聚类中心候选集Wo，即可排除异常点、离群点的影响。r一般取为样本平均距离Davg［16］，Davg的表达式如式（6）所示。

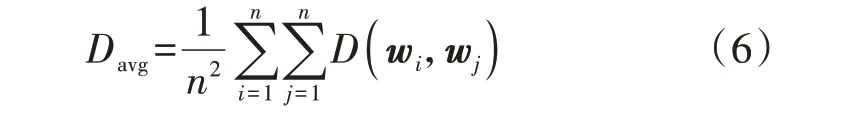
为进一步体现气象数据的局部密度特征，本文取r=Davg/2。由于随着W中样本数的增多，样本数据密度会提高，同时Wo中的样本数应随着K的增大而增加，因此，μ应正比于n/K。考虑到各季度间气候差异较大，气象数据聚合程度不同，若取μ=n/K，则可能导致某季度的Wo为空集，因此，本文在n/K的基础上对各季度的μ采取不同的经验系数进行修正。

2.1.3 算法流程

本文所提改进K-means 算法的基本思想是，通过提供可靠的初始聚类中心，以各气象模式间的风电功率预测误差分布函数差异最大化为导向，以预测精度水平高的气象模式对应的历史样本占多数的统计特性为约束条件，迭代进行经典K-means 算法计算，直到得到有效且合理的气象模式划分结果，具体流程如下。

1）根据某季度下的历史气象数据集W与历史风电功率预测误差数据集ΔP，利用肘部法确定该季度气象模式数K。

2）计算W中各样本点的数据密度，将其与密度阈值μ进行比较得到初始聚类中心候选集Wo，并从中随机选取zmax个点作为第1 个初始聚类中心的候选点集Wo，1（迭代次数z=1）。

3）取Wo，1中的第z个点作为第1 个初始聚类中心O'1，计算Wo中各点与该初始聚类中心的距离，取距离最远的点作为第2 个初始聚类中心O'2，计算Wo中其余各点与初始聚类中心O'1和O'2的最近距离，取距离最远的点作为第3 个初始聚类中心O'3，以此类推，直至求出K个初始聚类中心。

4）基于步骤1）与步骤3）所得聚类数与初始聚类中心，进行经典K-means 算法计算，得到相应聚类结果。

5）基于聚类结果对相应风电功率预测误差数据进行分箱，并分别对各箱误差数据拟合其概率密度函数。

6）校验聚类结果对应的指标Nkur是否大于60%：若是，则转至下一步；否则，返回步骤3），并取Wo，1中下一个点进行计算（z=z+1）。

7）计算聚类结果对应的目标函数SRMSE，比较相邻2 次聚类的SRMSE 大小，保存其值较大者对应的聚类结果。

8）重复步骤3）—7），直到SRMSE 大于阈值λ，即各气象模式间风电功率预测误差概率分布的差异足够大或满足最大迭代次数（z=zmax）。

2.2 基于SVM算法的气象模式识别

基于聚类分析所得的气象分类-误差分布的先验信息，在实际应用时需对NWP 给出的未来某时刻气象向量预测值进行准确分类判断，以提供相应的风电功率预测误差条件概率模型。考虑到SVM 算法在处理气象数据等高维输入空间的非线性分类问题时的高效性［17⁃18］，本文利用该算法对未来预测的气象向量数据进行模式识别。

由于SVM 只能解决二分类问题，当气象模式数大于2 时，采用一对一法［17］。为提高SVM 分类器的分类准确率，对主要影响参数惩罚因子C和核函数宽度θ采用网格搜索与三折交叉验证进行寻优［19］。定义分类准确率Iacc为：

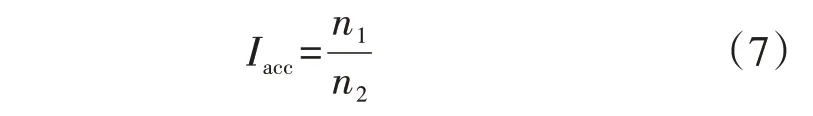
式中：n1为SVM准确分类的气象数据样本数；n2为识别的总气象数据样本数。

3 风电功率预测误差通用分布建模

本文在上述气象数据聚类过程中使用了核密度估计法来得到预测误差的概率密度函数曲线，该方法能真实地反映数据的概率分布情况，具有很高的精度且抗干扰数据能力强。然而，该方法得到的高拟合精度的概率密度函数没有解析表达式，在应用于随机调度决策问题时一般只能采用蒙特卡罗模拟对其进行处理，影响随机调度决策的效率。因此，本文进一步采用通用分布对各气象模式下的风电功率预测误差进行概率分布拟合。相比于正态分布与贝塔分布，通用分布能够对各种概率分布进行解析及准确表征，并且其累积分布函数CDF（Cumulative Distribution Function）可逆，有利于随机调度问题计算效率的提高［6］。

通用分布的概率密度函数表达式为：

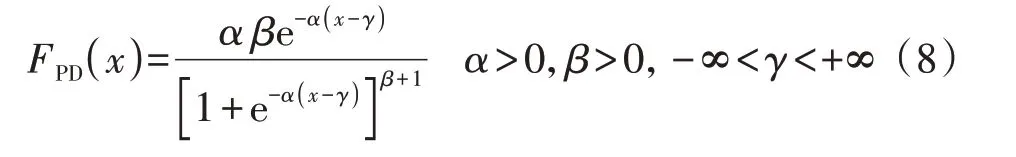
式中：FPD(x)为通用分布的概率密度函数，x为随机变量；α、β、γ为形状参数。基于式（8），可采用非线性最小二乘拟合法求出相应风电功率预测误差概率分布对应的通用分布的形状参数。拟合结果采用决定系数R2以及RMSE进行评估，R2表达式如式（9）所示。R2越接近1，RMSE越接近0，则表明拟合效果越好，模型准确度越高。

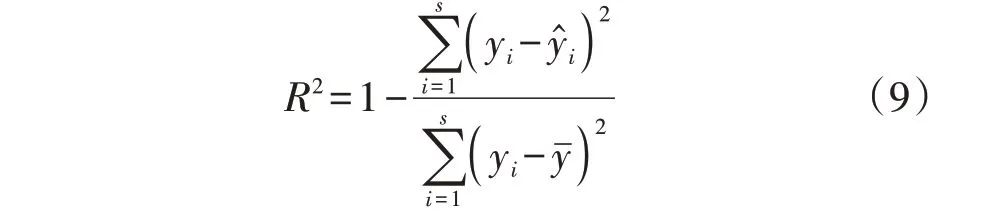
式中：yi为第i个待拟合值为yi的拟合值；yˉ为所有待拟合值的均值。

4 算例分析

本文利用中国华北地区某风电场2018 年全年每15 min 的实测历史气象数据及风电功率预测误差数据进行算例分析，所用数据均已采用删除法与0-1标准化进行预处理。此外，将所有数据按均匀随机采样的方式分成训练集和测试集，数据量之比为4∶1。

4.1 气象数据聚类效果分析

将历史气象数据（训练集）划分为4 个季度下的子集，分别采用肘部法得到各季度的SSE-K关系曲线，如附录A 图A3所示，第1—4季度气象模式数分别取为3、4、3、3。

利用改进的K-means 算法对各季度气象数据分别进行聚类，其中第1—4 季度μ的经验值分别取为n/( 10K)、n/( 6K)、n/( 10K)、n/( 6K)，SRMSE 的阈值λ取为0.02，可得到各季度的聚类效果如附录A 图A4所示，可见，各气象模式下的气象向量样本均有较明显的分群聚集现象，如以第1 季度为例，气象模式1呈现出低风速、东风的特性，气象模式2 为高温、西风，气象模式3 为低温、西风。对各气象模式下历史风电功率预测误差数据进行统计分析，得到对应的预测误差概率密度函数曲线，如附录A 图A5 所示，可见，各气象模式对应的风电功率预测误差概率分布间有较明显的区别。

为进一步验证各气象模式下预测误差概率分布间的差异性，采用经典K-means算法对第3季度的气象数据样本进行聚类，得到多种聚类结果，计算各聚类结果对应的SRMSE，取其中最优的聚类结果与改进K-means 算法的聚类结果进行对比，如图3 所示。在经典K-means 算法产生的多种聚类结果中，其SRMSE 最大为0.019 4，而本文所提改进的K-means算法所得结果的SRMSE 为0.022 7，可见，以分布函数差异化为导向的改进的K-means 算法能得到预测误差概率分布间差异最大的气象数据聚类划分。同时，第1—4 季度聚类结果对应的Nkur分别为60.63%、74.63%、61.77%、60.06%，均在60%以上，这表明满足预测精度水平较高的气象模式对应的历史样本占多数的统计特性要求。

图3 改进的K-means算法与经典K-means算法所得概率密度函数曲线Fig.3 PDF curves obtained by modified K-means algorithm and classic K-means algorithm

4.2 气象模式识别效果分析

基于前述聚类分析结果，对训练集气象数据进行SVM 气象模式识别训练。采用网格搜索与三折交叉验证进行参数寻优，再基于训练结果利用测试集对SVM 的分类准确率进行校验。为避免过拟合带来的训练结果泛化性较差或者欠拟合带来的识别准确率较低，设置C与θ的变化范围均为［2-3，27］，变化步长均为20.5。此外，如果将基于所有数据（包括训练集和测试集）的气象数据分类结果作为标准，则可在测试集上校验训练集得到的SVM 的气象模式识别正确率。表1 给出了利用训练集数据得到的各季度SVM参数寻优及校验结果。

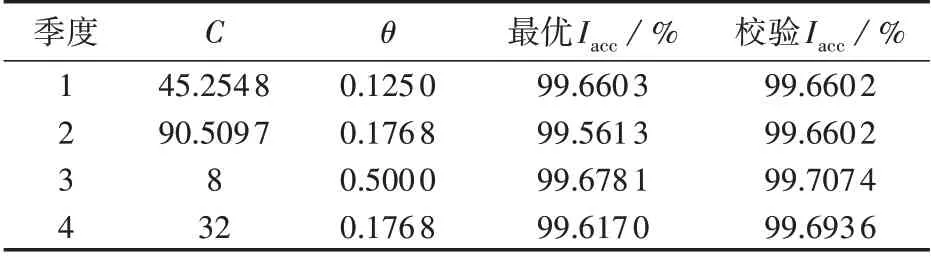
表1 各季度SVM参数寻优及校验结果Table 1 SVM parameter optimization and verification results in each season

由表1 可见，各季度SVM 的最优分类准确率均在99%以上，能满足在实际调度计算时根据NWP信息匹配出相应气象模式的需求。经过SVM 识别后，对测试集下各气象模式对应的预测误差数据进行概率统计，得到的概率密度函数曲线（第1 季度）如附录A 图A6所示。可以看出，同一气象模式下训练集误差数据和测试集误差数据的概率分布较为接近，这也在一定程度上说明了将气象模式作为风电功率预测误差条件概率中的先验条件的正确性。

4.3 通用分布建模结果

基于4.1 节得到的各气象模式下风电功率预测误差概率密度函数曲线，利用通用分布和非线性最小二乘法进行拟合，得到各季度各气象模式下预测误差的通用分布模型参数及对应的评价指标，如表2 所示。取第1 季度各气象模式下预测误差的通用分布概率密度函数曲线与原始概率密度函数曲线进行对比，如附录A 图A7所示。上述结果均表明通用分布可以比较准确地表征风电功率预测误差的概率分布。同时，通用分布良好的解析特性也有利于高效解决考虑风电功率预测误差的随机调度决策问题。

表2 风电功率预测误差通用分布建模结果Table 2 Modeling results of versatile distribution for wind power forecasting error

4.4 基于简单随机经济调度问题的应用分析

本节将进一步通过一个简单的考虑风电功率预测误差不确定性的随机调度决策问题来说明风电功率预测误差分布函数差异化导向的气象模式分类的有效性。为与本文所提的基于气象模式分类的风电功率预测误差条件概率模型进行对比，设置不考虑气象信息的简单统计频次模型（简称对比模型），即各调度时刻的预测误差服从相同的概率分布（由历史预测误差数据拟合得到）。

本节所使用的随机调度决策问题是一个理想化的单时间断面随机最优潮流问题，数学描述如下：

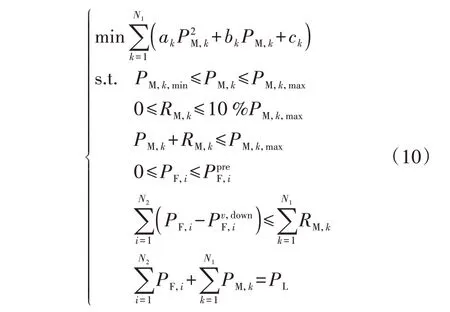
式中：N1为火电机组数；ak、bk、ck为第k台火电机组的燃料成本系数；PM，k为第k台火电机组的出力；PM，k，min、PM，k，max分别为第k台火电机组的最小、最大出力；RM，k为第k台火电机组的上备用；PF，i为第i座风电场的出力；为第i座风电场的风电功率预测值；N2为风电场数；为置信度v下第i座风电场的出力分布范围下界（零出力对应的置信度为100%）；PL为系统总负荷。该决策问题可描述为：给定某一置信度下风电场出力的下限，在满足发电-负荷平衡的要求下，调整火电机组的出力来实现尽可能小的燃料费用（即尽可能多地利用风能）。火电机组出力越低，则认为风电出力越高，风电调度出力与出力下限的差距越大，将有可能无法满足火电机组最大备用要高于该差距的约束条件，此时系统可能会损失负荷。可以看出，该决策问题的解决依赖于对某一高置信度下风电出力下限的准确估计。

根据上述模型，本文以包含1座风电场和6台火电机组的7 机系统为仿真对象，火电机组参数如附录A 表A1 所示。风电场的数据来自于前述中国华北某实际风电场的实际数据并进行适当的容量折算。基于该风电场2018 年3 月24 日至3 月31 日的历史气象数据及风电功率预测实际值，在8 d 中，每15 min进行1次总共进行768次随机最优潮流计算。分别采用2 种模型估计风电场出力下限（置信度取为0.95），结果如图4 所示。引入历史风电功率实际值作为对比，实际值位于2 种模型所估计下限以上的概率（下限覆盖率）如表3 所示。下限覆盖率越高说明所估计下限的可信度越高。可见，对比模型由于未进行分布函数差异化导向的条件化建模，所估计的下限更低，从而覆盖率更高，但2 种模型对应的下限覆盖率相差较小且均在97%以上，即均具有较高的可信度。同时，排除由预测值较低而导致的基于2 种模型所估计的下限均为0 的情况，8 d 内基于本文模型所确定的风电功率下限更优的比例达到88.44%。这表明本文模型在保证结果可信的同时也能满足准确性的要求，即预测误差的建模精度更高。

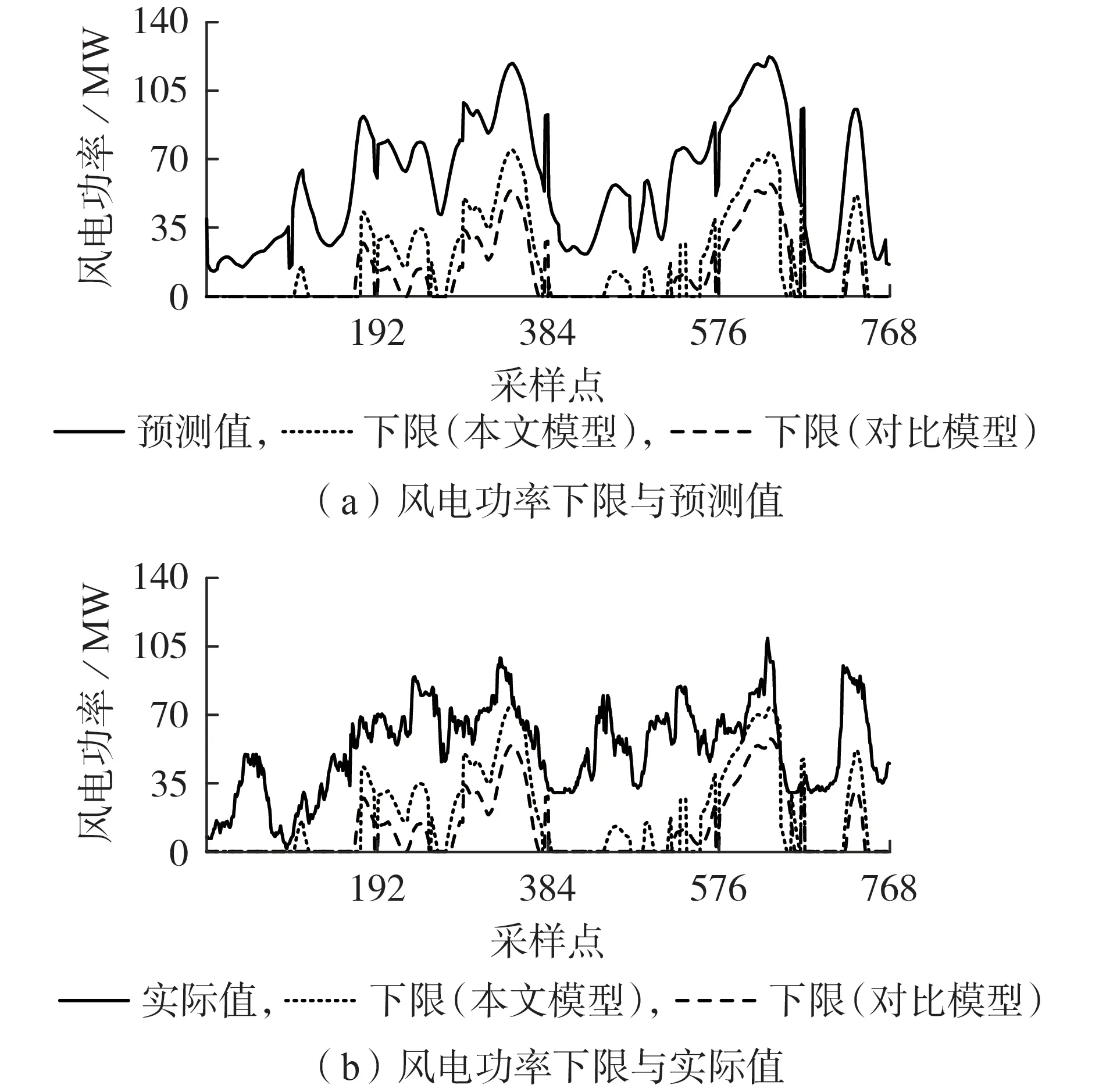
图4 2种预测误差概率模型得到的风电功率下限Fig.4 Lower limits of wind power obtained by two probability models of forecasting error

表3 随机调度决策问题的计算结果Table 3 Calculation results of stochastic dispatch and decision making problem

图5 与表3 给出了2 种模型的调度结果。可见，对比模型在风电功率预测值较高时所确定的风电功率调度值均明显低于风电功率预测值（由于基于预测误差概率分布给出的风电出力下限均较低），而本文模型在多数情况下给出的可信的风电出力下限均接近风电功率预测值（即不需要过大的火电备用容量），从而决策的风电调度值均为预测值。采用本文模型进行随机调度决策计算时，系统风电消纳量相比对比模型增加了495.67 MW·h。

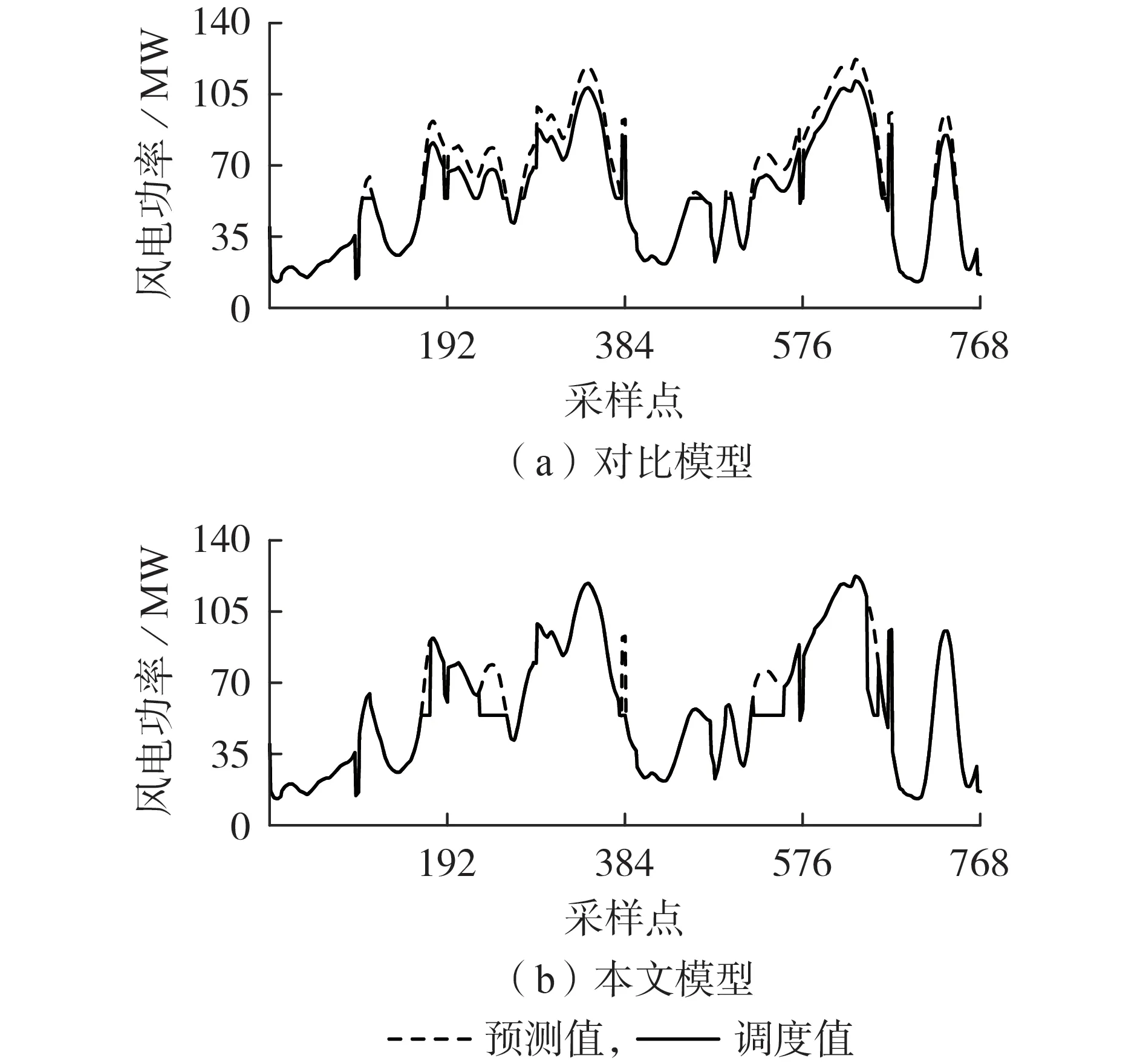
图5 2种预测误差概率模型得到的风电调度曲线Fig.5 Wind power dispatch curves obtained by two probability models of forecasting error

综上所述，基于分布函数差异化导向的风电功率预测误差气象条件概率建模方法，能保证用于随机调度决策的气象模式-误差分布先验信息的有效性，因此，能从统计学角度提升系统消纳随机性风电的水平。

5 结论

本文考虑气象对预测精度的影响，提出一种分布函数差异化导向的风电功率预测误差气象条件概率建模方法，得到的主要结论如下。

1）先验信息对于随机调度决策问题的价值在于条件概率分布本身的差异性。算例表明，相较于不区分预测误差区别的统计频次建模方法，以分布函数差异化为导向的风电功率预测误差条件概率建模方法在应用于随机调度决策时可以获得统计意义上更优的调度结果，提升风电消纳水平。

2）气象条件与风电功率预测精度紧密相关，可以基于气象和风电功率预测误差数据挖掘二者的对应关系。基于实际数据的仿真分析表明，以风电功率预测误差概率分布函数差异性最大化为目标，多维气象数据具有良好的聚类特性，验证了气象数据作为预测误差水平先验条件的有效性。

附录见本刊网络版（http：//www.epae.cn）。