基于相对几何不变性的点云粗配准算法研究

陈亚超，樊彦国，樊博文，禹定峰

1.中国石油大学（华东）海洋与空间信息学院，山东 青岛 266580

2.哈尔滨工程大学 水声工程学院，哈尔滨 150001

3.齐鲁工业大学（山东省科学院）山东省科学院海洋仪器仪表研究所，山东 青岛 266061

配准技术的研究主要是从特征提取、粗配准算法、精配准[1-3]算法三个方面去改进提高[4]。而精配准对初值具有较高要求，所以在大数据场景下亟需一个效率高、精度高、稳定性强的粗配准算法。点云粗配准中匹配对获取主要依靠点云的局部特征，Rusu等提出了著名的点特征描述子（point feature histogram，PFH）[5]和快速点特征描述子（fast point feature histogram，FP‐FH）[6]，算法兼具特征差异性和运行效率；而在近年也涌现出了差异性更强的SHOT（signature of histograms of orientations）[7]，RoPs（the rotational projection statis‐tics）[8]等描述子。由于不同描述子的特性，产生了多种点云粗配准算法，Aiger等[9]提出著名的四点一致集（4-points congruent sets，FPCS）算法，算法依据两点对的仿射不变性，寻找稳定结构，但算法要求较高，参数难以设置，稳定性差。而后Rusu等提出采样一致性初始配准（sample consensus initial alignment，SAC-IA）[6]算法，依靠随机采样一致性算法和FPFH描述子获取配准初值，算法计算量大，且控制参数较多。针对此算法，Bu‐ch等[10]在SAC-IA随机选点的基础上考虑了几何距离，加快了算法速度，但仍需定义大量控制参数。近年来，国内学者也对粗配准算法有大量研究，张晗等[11]在SAC-IA基础上考虑点位间角度特征，提高了配准效率；刘世光等[12]提出基于边界带查找的FPCS改进算法，使得FPCS算法更加稳定；侯彬等[13]对现有的特征描述子进行了粗配准对比，分析了特征描述子的适用情况；在配准效率问题上，研究者们也提出了多种基于关键点提取的粗配准算法，但大部分粗配准算法仍需设置大量控制参数，稳定性较差。

根据以上研究进展与分析，为了解决粗配准算法稳定性差及控制参数难以设置等问题，本文提出一种基于关键点的相对几何不变性特征的粗配准算法（keyrelative geometric invariance initial alignment，K-RGI），算法为了在大数据下的可用性，采取对关键点进行匹配对选取的策略，通过关键点提取算法获取一定量的点云，应用FPFH特征进行最邻近匹配对初步筛选，然后通过在源点云与目标点云上的对称候选寻点策略及两组匹配对连接边的2-范数比例不变性，精确获取可靠的匹配对，最后通过奇异值分解（singular value decomposition，SVD）算法求解多元线性最小二乘目标函数。实验结果表明，本文算法相比传统粗配准算法，时间和精度都有显著提升，且参数更易设置，在真实场景下，算法表现优异。

1 点云粗配准相关原理

1.1 数据预处理

激光扫描仪获取的点云数据一般都是无序散乱的，而获取过程中不可避免地存在许多冗余点和噪声点，且真实场景需要海量点云数据进行表达，所以直接获取的原始数据需要经过预处理过程得到便于计算的数据结构和体量，如图1所示，通常点云预处理包括拓扑邻域的建立、法线计算、点云噪声去除、点云数据量压缩等过程。拓扑邻域采用kdtree（k-dimension tree）数据结构进行构建，便于最邻近搜索。法线计算主要依靠目标点邻域范围内的最小二乘拟合平面求出，一般通过邻域最小特征值方向近似代替。点云噪声去除分为离群点与噪声浮点，离群点采用统计滤波算法，浮点采用双边滤波[14]算法。点云数据压缩则构建点云整体的八叉树结构，通过立方体内密度去除冗余点。

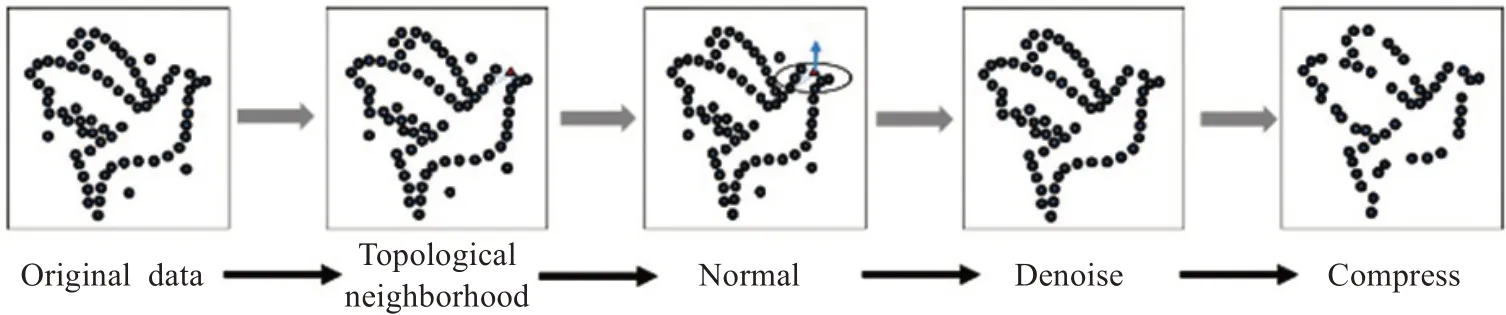
图1 点云预处理流程示例Fig.1 Example of point cloud preprocessing process

1.2 关键点提取

常用的关键点提取包括八叉树结构数据过滤法，内部 签 名 法（intrinsic shape signatures，ISS）[15]，Har‐ris3D[16]关键提取法、尺度不变特征变换（scale-invariant feature transform，SIFT）[17]等，针对不同提取算法特点，八叉树结构过滤法属于区域降采样以获取更少量的点云数据，但并不能剔除平面点，而SIFT计算需要强度属性，对于一般的点云数据并不适用，所以结合ISS与Har‐ris3D的算法特点，两者均通过特征值与关键点的相关关系进行筛选，适用范围广，且计算简单，对于点云关键点提取步骤，两种算法通过合理的参数设置均可适用于提取边缘点或角点。

ISS主要通过控制计算点邻域范围内特征平面与关键点的关系进行提取，通过计算局部邻域范围内坐标协方差矩阵的特征值，对其排序后设置阈值，ε1和ε2控制关键点输出条件：

Harris3D则是从Harris2D提取算法衍生而来，关键点提取依据为一定大小的立方体轴向移动，相应体内点数量变化情况。在Harris2D算法中，通过各向灰度梯度值描述变化，针对点云描述，Harris3D[16]采用各点法向量类比梯度，则变化矩阵M为：

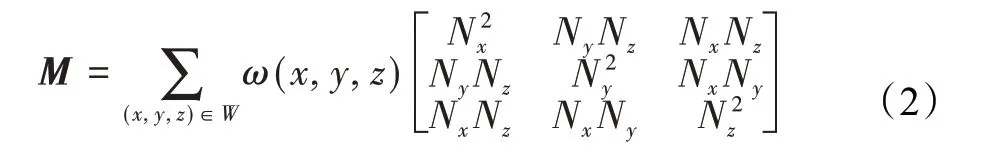
式中，W为滑动立方体，ω为窗体函数，表示不同窗体的权重，Nx,Ny,Nz表示点法向量的轴向分量。

进而可计算Harris3D响应值控制关键点输出条件：

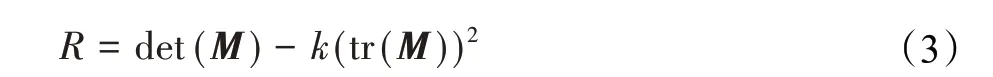
式中，R为Harris响应值，det为矩阵的行列式，tr为矩阵的迹，k为常量用于扩大响应值区别。

1.3 点云粗配准基本原理

点云配准即两个点云数据，点云源数据S与点云目标数据T，主要依靠求得一定量的匹配对，构建以下目标函数，求取齐次旋转矩阵R：

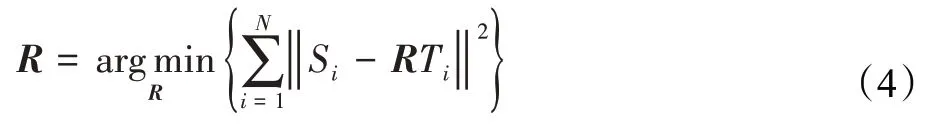
式中，R为4×4的旋转平移齐次矩阵，N为源点云与目标点云匹配对的数量，Si、Ti为第i个匹配对在源点云与目标点云中的坐标值。

为了能够准确获得配准结果，需要寻找三个以上的正确匹配对，以满足三维空间的坐标转换。配准需要通过局部邻域特征进行最邻近匹配，其中具有代表性的SAC-IA算法，使用FPFH作为特征匹配描述子，通过随机选择点机制和迭代计算机制寻找合适的旋转矩阵，主要步骤如下：

（1）计算源点云与目标点云各点的FPFH描述子。

（2）在S源点云中选择3个以上的随机样本点，同时确保它们的成对距离大于用户定义的最小距离dmin。

（3）对于每个样本点，在T目标点云中找到直方图与样本点直方图相似的点列表。从这些中，随机选择一个将被认为是样本点的对应。

（4）计算由样本点及其对应关系定义的刚性变换，并应用变换矩阵计算源点云变换后与目标点云的误差度量，若不符合要求，回到（2）重新随机选择，直到达到误差要求或迭代最大数。

由算法过程可知，SAC-IA算法的随机机制使得参数设置较为困难，迭代机制使得匹配对查找过程若出现匹配对错误将降低计算效率，目前基于特征匹配下的粗配准算法仍然以随机与迭代机制为主要计算框架，粗配准算法中本质的随机与迭代机制是阻碍效率与精度的关键。

2 基于相关几何不变性的粗配准算法（K-RGI）

本文配准算法则以更精准快速地获取匹配对及更易设置控制参数为目的，受源点云与目标点云匹配对之间几何特性的启发下，提出基于相关几何不变性的粗配准算法（K-RGI），算法主要思想是从关键点中利用计算量小差异性强的FPFH描述子进行初步匹配对筛选，而后通过多步策略剔除错误对，获取更精确的匹配结果，该算法能够有效快速获取匹配对的核心点在于三大策略的提出：

（1）对称候选寻点策略

对称候选点剔除指在源点云中某点Si寻找目标点云中特征直方图最邻近的n个候选点T1,T2,…,Tn，记Tj为Si的第j个候选点，再对称通过目标点云中的候选点T1,T2,…,Tn分别查找其在源点云中特征直方图最邻近的n个点得到TSj1,TSj2,…,TSjn，记TSj为Tj的对称候选点，若TSj1,TSj2,…,TSjn中至少存在一个与Si为同一点，取相应候选点为匹配对应点，得到匹配对{Si,Tj}，若不存在则无对应匹配，如图2所示。

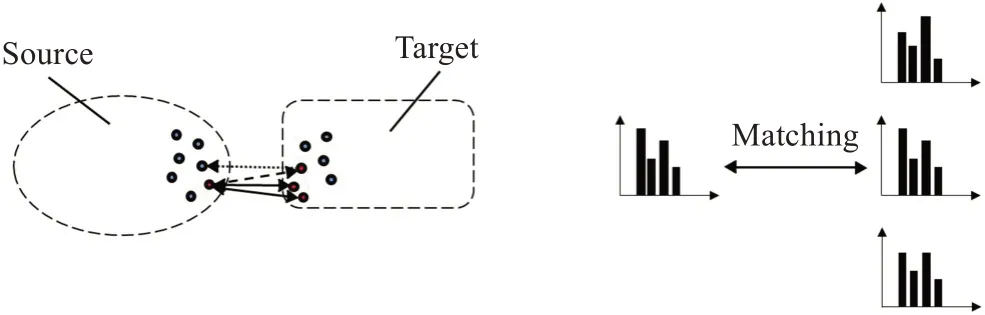
图2 对称候选寻点示例Fig.2 Example of symmetric candidate point elimination

（2）相对几何不变性筛选策略

相对几何不变性指若存在正确的两组匹配对{S1,T1},{S2,T2}，满足条件：

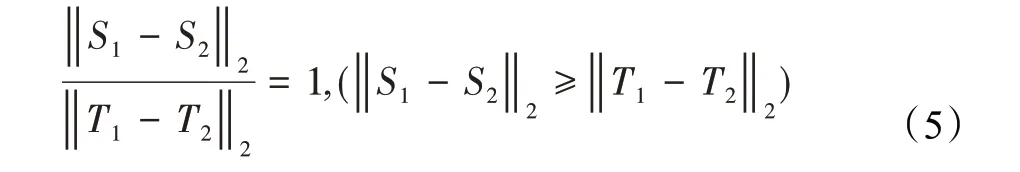
式中S1、S2表示源点云的两点，T1、T2表示目标点云的对应点，‖‖2表示向量2-范数。如图3所示，由于点云数据的无序散乱性，及点云采集结果的不唯一性，无法找到完全正确的匹配对，但考虑到误差影响，实际中正确的匹配对的公式（5）结果仍然在1的小范围内，因此，只需要判断筛选出的匹配对按公式（5）计算后是否保持在比例阈值中即可。

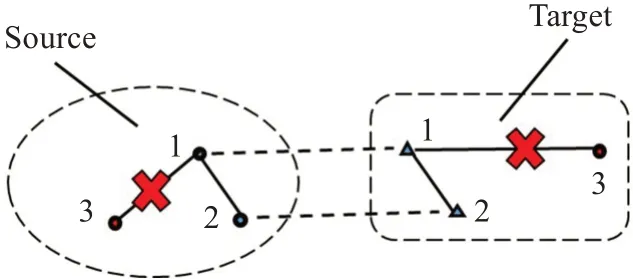
图3 相对几何不变性示例Fig.3 Example of relative geometric invariance

对于三维空间来说，仅仅使用两组匹配对并不能完全说明匹配正确，所以实际计算中将匹配符合公式的两组匹配点分别列为候选点并对应计数，由于正确的匹配对在计算过程中会多次被使用形成稳定的多边形非共面几何结构，所以当统计数大于计数阈值时，匹配对则可信任，阈值根据数据量自定义设置。

（3）重叠区域连续性搜索策略

针对几何不变性，需要确定一种查找策略，而不是随机选取两点进行计算，如图4所示，通过点云数据观察，可发现重叠区域在局部范围内都是连续的，匹配对必然存在于重叠区域，所以通过匹配对连续性，本文提出待匹配点的空间邻域搜索策略，即在现有匹配对中，在源点云中建立源匹配点的稀疏kdtree结构，通过每个源匹配点的k邻域感知野，k设置为源匹配点总数的倍数，分别与其邻域点连接，计算公式（5）并依据结果计数统计。

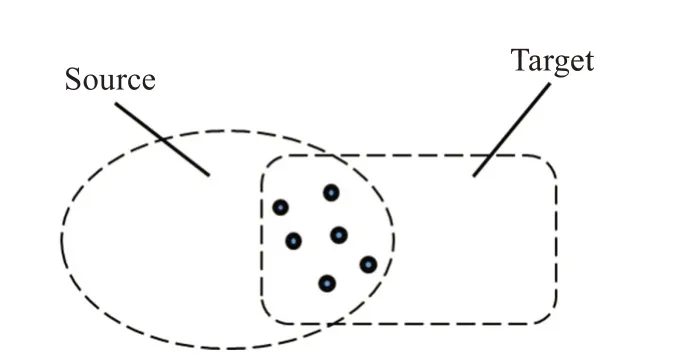
图4 重叠区域匹配对连续性示例Fig.4 Example of matching pairs of overlapping regions

由点云配准原理可知阈值的选取对结果尤为重要，K-RGI三大策略中对称候选阈值表达了对特征描述子匹配结果的信任程度，当点云数据特征不明显时，可调整到较大阈值，当数据特征差异明显时，可设置较小阈值，取3~5个候选数在准确率和运行时间平衡上更为通用。几何比例阈值表达了匹配对之间的几何差距程度，采用去单位化的比例形式阈值比传统的绝对阈值更加方便有效，按实际精度要求设置即可，一般设置为1.01~1.03。感知野倍数阈值表达了对重叠区域的预估程度，根据实际数据重叠的预估程度设置源匹配点倍数为0~1之间，对于无法预估重叠的未知数据及对运行时间的考虑，一般设置0.5倍即可。计数阈值表达了匹配对准确程度，感知野区域越大，匹配点的总计算次数越多，若匹配点被统计的次数越多，则结果越准确，一般设置2~3次即可保证大部分匹配对是正确的。

当匹配对确定后，由于粗配准不需要完全精确的配准结果，后续只需利用3个以上的匹配对求解点云配准目标函数，常用的计算方法有奇异值分解法（SVD）和LM（Levenberg-Marquardt）法，对于多元线性最小二乘方程，两种方法求解结果一致。

综上所述，基于相关几何不变性的粗配准算法（KRGI）的算法描述为：

（1）设置对称候选阈值，几何比例阈值，感知野倍数阈值，计数阈值并输入源点云与目标点云，进行预处理。

（2）通过ISS或Harris3D算法提取源点云与目标点云的关键点。

（3）分别计算源点云与目标点云中关键点在原数据基础上的FPFH描述子。

（4）利用特征直方图最邻近搜索与对称候选寻点策略，筛选初步匹配对。

（5）构建筛选后的源匹配点的kdtree结构，利用重叠区域连续搜索策略，对各计算单元通过相对几何不变性得到候选匹配对，并进行计数统计。

（6）选择计数大于计数阈值的匹配对，若大于三对则利用SVD或LM算法求解目标函数，若匹配对数量不足则返回步骤（2）提取更多关键点。

3 实验结果与分析

3.1 实验概述

以Intel core i7，2.5 GHzCPU，8 GB内存的Linux虚拟机作为实验平台，应用PCL（point cloud library）[16]库对Stanford实验室提供的含有437 645个点的Dragon三维数据进行算法实验对比。为解释关键点引入的必要性及更客观地验证实验对比结果，根据特征和方法的不同选用对比算法，通过对工业软件及近年科研成果相关调研，为突出实验的综合性与前沿性，采用非关键点提取的SAC-IA-FPFH[6]算法、SAC-IA-SHOT[6-7]算法、SAC-IA-PRE[10]算法及关键点Harris3D[16]算法提取下的K-SAC-IA-FPFH算法、K-SAC-IA-SHOT算法、K-SACIA-PRE算法、K-SAC-IA-FEA[11]算法、K-FPCS[9]算法和本文算法K-RGI。各算法控制参数数量如表1所示，本文算法K-RGI实验参数设置为通用型数值，其中对称候选阈值为3，几何比例阈值为1.01，感知野倍数阈值为0.5，计数阈值为2，另外八种算法参数值设置为PCL源码的默认值。从表中可观察到本文算法比其他算法参数设置数量减少了2~3个，且部分参数设置从绝对距离改进为比例设置，对于尺度不同的数据参数更易设置。

表1 粗配准算法控制参数数量表Table 1 Control parameters quantity of each coarse algorithm

3.2 误差与效率分析

为比较粗配准算法的匹配误差与效率，采用Dragon数据随机执行旋转平移，通过对比其初始位置获得实验结果如图5所示，各算法在相同参数设置一致情况下，本文算法表现良好，证明了算法的有效性，为进一步对比实验细节，对各算法的旋转误差，平移误差及时间效率进行对比，结果如图6、图7所示，图6误差结果表明本文算法相比其他算法具有较高配准精度，且证实了FPFH特征描述子时间和特异性上的优势，而图7结果表明，引入关键点能显著提高计算效率且本文算法在效率上同样优于大部分粗配准算法。

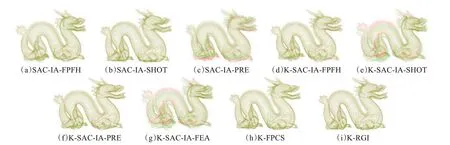
图5 龙点云配准效果Fig.5 Registration effect of dragon point cloud

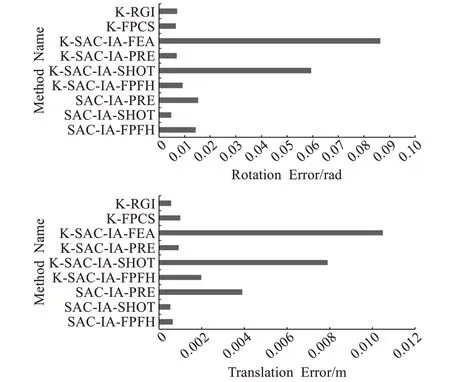
图6 粗配准算法旋转与平移误差对比Fig.6 Comparison of rotation and translation errors of coarse registration algorithms

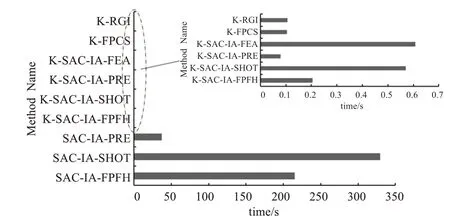
图7 粗配准算法时间效率对比Fig.7 Comparison of time efficiency of coarse registration algorithms

3.3 算法稳定性分析

为进一步说明算法稳定性，采用关键点提取下的粗配准算法，通过多次实验观察结果变化，调整迭代次数为500~5 000次，旋转平移误差及时间效率变化如图8、图9所示，实验结果表明，当迭代次数设置较少时，传统算法可能出现算法误差偏大问题，设置过多又会导致时间效率低下。由于传统算法的随机机制，算法稳定性较差，而本文算法在误差和效率方面均能保持稳定结果，证明了本文算法的稳定性优于其他算法。

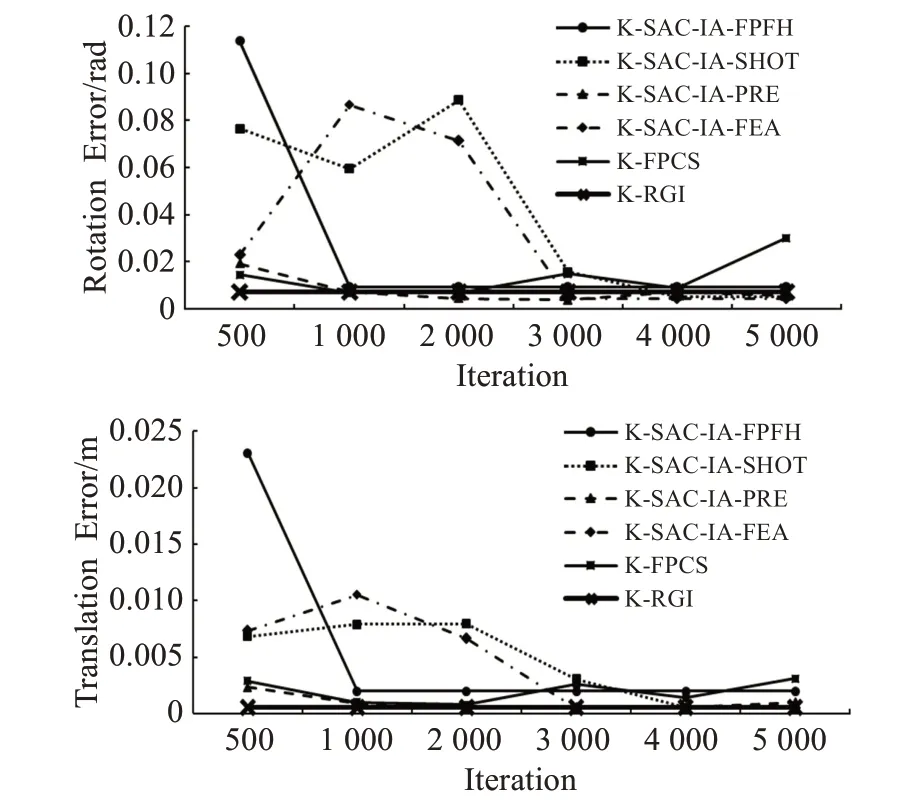
图8 粗配准算法旋转与平移误差对比Fig.8 Comparison of rotation and translation errors of coarse registration algorithm with number of iterations

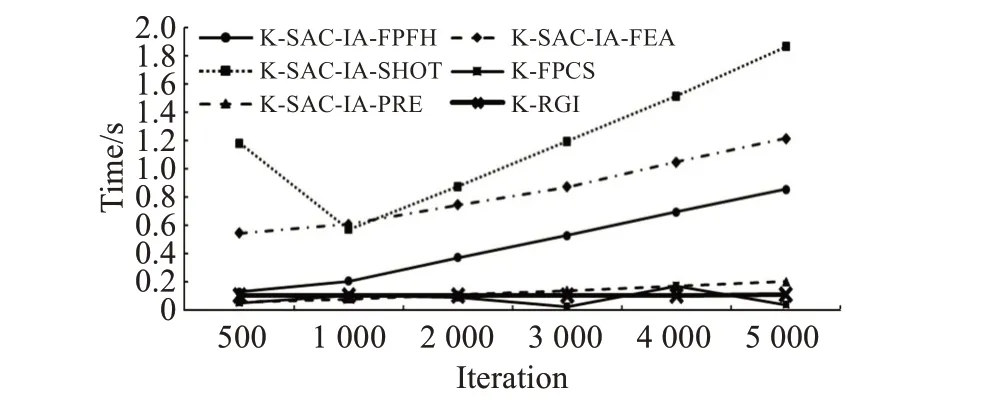
图9 粗配准算法随迭代次数的时间效率对比Fig.9 Comparison of time efficiency of coarse registration algorithm with number of iterations

3.4 真实场景粗配准分析

为验证关键点提取下的粗配准算法的实际应用效果，采用PCL提供的含有103 266个点的真实牛奶扫描数据进行再次实验，分割提取其中一个牛奶盒，并作随机旋转平移，在仅有30%重叠率及桌面和其他物品干扰下，进行部分粗配准实验对比。如图10所示，图10（e）结果表明由于点云结构未满足FPCS算法要求而导致计算失败，图10（f）表明本文算法结果具有良好的配准效果，能够稳定地应用到真实场景中。

图10 牛奶点云配准效果Fig.10 Registration effect of milk point cloud

4 结束语

提出在关键点提取下的基于几何不变性的粗配准算法，与传统算法实验结果对比表明，本算法在参数设置及稳定性上具有显著优势，在精度及效率上高于大部分粗配准算法。在实际应用场景及使用者角度提供了一个在时间和精度上能够满足需求，参数设置更简单，稳定性更强的粗配准算法。

粗配准算法仍然存在需要用户自定义设置参数的问题，不利于工业自动化应用，因此，下一步工作是在现有信息中尽可能通过算法获得自适应参数，简化操作流程。