分层学习的边缘计算资源调度粒子群优化算法
胡晓敏,陈镇填,李 敏,2
1.广东工业大学 计算机学院,广州 510006
2.广东工业大学 信息工程学院,广州 510006
随着物联网行业的发展,智能移动设备的数量快速增长,相应的智能移动应用服务程序也越来越多,在教育、商业、游戏、安全和医疗保健等各个领域都有相关的智能移动应用程序[1]。这些应用程序要求设备提供较高的服务质量,如低延迟、数据安全和隐私保护,并且一台智能移动设备上往往会运行多种应用程序,对设备的硬件条件,特别是设备的计算能力和电池容量提出了较高的要求。然而,智能移动设备具有便携性和移动性的特点,其硬件条件无法满足应用程序的服务质量需求。边缘计算技术为解决智能移动设备在计算资源和能耗上的需求提供了手段。
边缘计算是指在网络边缘执行计算的一种新型计算模型[2],通过使用部署在网络边缘的设备(如工作站、通信基站等)对终端设备(如智能家居、移动设备等)产生的数据进行处理,由边缘计算设备提供计算能力,大大降低了对终端设备的硬件要求。如何更有效地利用边缘计算设备的资源,降低终端设备的能耗,成为了边缘计算资源调度的核心问题。针对这一问题,越来越多的研究人员通过研究计算卸载决策(computation offloading decision)和资源分配(resource allocation)这两个方面来减少设备的能源消耗。Yang等人[3]在一个多服务器,多用户设备构成的计算模型中,针对移动设备能耗问题提出了改进的分支定界算法,从卸载决策和计算资源这两方面进行优化,降低移动设备的能源消耗。Guo等人[4]则提出了一种基于计算算法的遗传算法(genetic algo‐rithm based computation algorithm),用于多服务器和多用户设备组成的边缘计算模型的能耗优化问题,通过卸载决策,信道分配和资源分配这三个方面来降低用户设备的能源消耗。Huang等人[5]提出多用户合作的移动边缘计算卸载系统,移动设备不仅可以将计算任务卸载给边缘服务器完成,也可以选择卸载给其他空闲的移动设备。为了降低移动设备计算能耗,作者提出了一种基于蚁群算法的双层优化方法,对移动边缘计算中的任务卸载决策和资源分配问题进行联合优化,在满足延迟约束下使得所有移动用户的总消耗最小化。
在边缘计算能耗优化问题上需要对多方面资源进行合理的调度,如网络信道分配、数据分流比例和计算资源分配,并且还会考虑最大延迟等多方面约束。因此边缘计算的能耗优化问题是一个复杂的非线性规划问题[6],传统的数学优化算法无法在合理的时间内得到其最优解。
模拟自然界群体协作寻优的群体智能算法,凭借其强大的全局搜索能力和寻优能力,更少的计算代价和更快的收敛速度被广泛应用。其中粒子群优化算法具有收敛速度快,设置参数少等特征,是求解一些实际工程问题的首要选择。根据利用粒子群算法优化计算卸载问题的方式,已有的做法可以分为三类:第一类是对粒子群算法的操作进行改进。如Adhikari等人[7]提出的加速粒子群算法,使用全局最优个体来更新个体的速度和位置,目的是提高算法的收敛速度。Deng[8]和Wang[9]等人改进了粒子群算法的惯性系数计算公式,根据粒子的适应度值动态地改变惯性系数。第二类是把粒子群算法与其他进化算法相结合。如Chen等人[10]将粒子群算法与遗传算法相结合,解决卸载深度网络中间层的决策问题。第三种是利用粒子群算法解决任务卸载问题中的子问题。如Zhou等人[11]为解决超密集异构网络中的计算卸载问题,先采用遗传算法进行粗粒度搜索,再用粒子群算法进行细粒度搜索得出最优的计算卸载决策。Xue等人[12]提出粒子群和遗传算法相结合的算法用于大型深度神经网络的迁移决策问题,提出层合并上传算法解决上传问题。Liu等人[13]则将概率任务卸载问题分解成多个无约束子问题,使用粒子群算法去求解每个子问题从而得到概率任务卸载问题的最优解。
然而,上述提到的研究中都只是研究如何降低智能移动设备端的能耗和网络传输的能耗,很少将边缘服务器端的能耗作为优化目标。对于提供云计算服务的企业来说,他们需要考虑如何充分利用服务器的计算资源,降低服务器的能耗,增加机器的使用时间,减少企业成本。受此启发,针对优化资源配置,减少设备能耗问题,本文对与计算任务和计算能耗的相关参数进行建模,将降低服务器能耗作为优化目标之一,提出了与移动设备计算能耗、数据传输能耗和边缘服务器计算能耗相关的总能耗公式,并且增加了对边缘服务器相关计算资源的限制作为新的约束条件,如边缘服务器的存储约束,最大能耗约束和CPU周期约束。
本文采用粒子群算法对总能耗优化问题进行求解,优化每台移动设备对于移动设备的计算速度,下载数据功耗,数据卸载百分比和剩余网络带宽占这四个参数的取值,更合理分配计算资源使得总能耗最小。针对粒子群存在容易陷入局部最优和种群多样性低等问题,本文引入分层学习策略对算法进行改进,通过分层学习的方式保存种群粒子的多样性和提高算法全局搜索能力,并将改进的算法称为基于分层学习的粒子群算法(levelbased learning swarm optimizer,LLSO)。
1 问题建模
1.1 系统模型
考虑到智能移动设备有限的计算资源,无法按需求完成计算任务,需要将部分或者全部计算任务传输给边缘服务器处理,因此提出了用于联合优化的计算分流系统模型,如图1所示。在图1中,假设存在M台智能移动设备和S个支持上行和下行功能的传输通道,M台智能移动设备可以通过S个传输通道发送自己的计算数据和接受边缘服务器的计算结果,并且传输通道之间不存在干扰。优化算法会收集智能移动设备和边缘服务器的硬件资源信息,并且收集移动设备需要运行的计算任务和相关约束,在满足所有约束条件的情况下,如计算延迟约束,移动设备和服务器的最大能耗约束等,决定每台设备最优的执行方案,合理地调整计算资源和规划计算任务卸载比例,从而能够消耗最少的移动设备计算能耗,传输能耗和边缘服务器计算能耗。
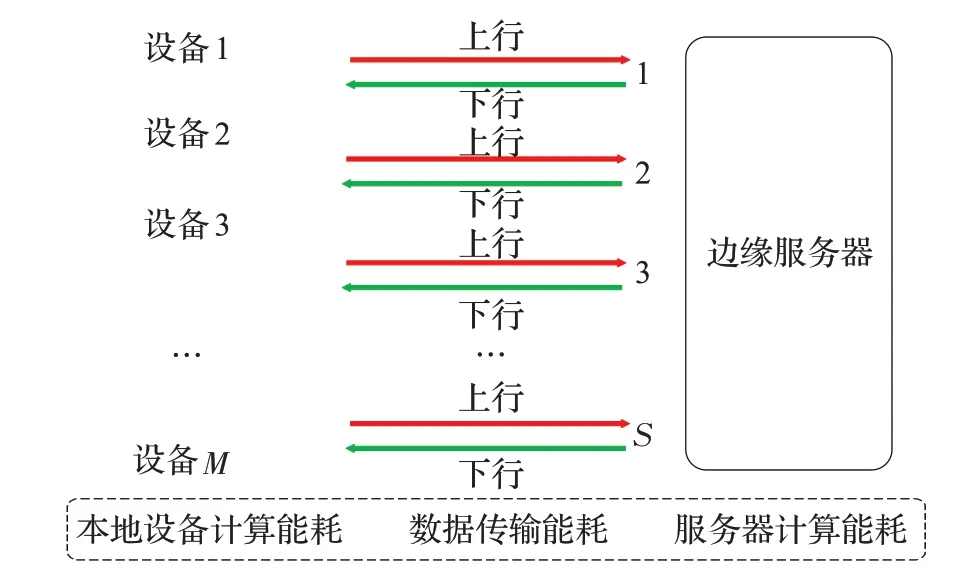
图1 计算卸载系统模型Fig.1 Computation offloading system model
1.2 能耗优化建模
智能移动设备和边缘服务器的总能耗是由每台智能移动设备的本地计算能耗ELm,服务器处理每台智能移动设备分流数据产生的计算能耗ECm以及数据传输过程产生的传输能耗ηm这三个方面构成,计算公式如下:
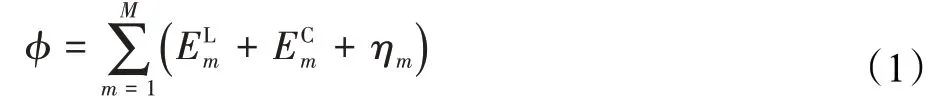
每台智能移动设备的本地计算能耗ELm与设备的计算功率和工作时长有关[14],用PLm表示单台智能移动设备的计算功率,用tLm表示单台智能移动设备的工作时长,因此可以得到本地计算能耗ELm的计算公式为:

以上公式中计算功率与智能移动设备的计算速度有关。用fm表示编号第m台智能移动设备的计算速度,单位cycle/s,因此,智能移动设备的计算功率可以通过下面的公式计算得到:

其中,kL为智能移动设备芯片结构相关的一个常数,其值与移动设备的硬件条件相关。
工作时长与智能移动设备需要处理的计算数据量和数据复杂性相关,数据量越多,数据的复杂性越大,计算速度越慢,需要的工作时长就越长。根据文献[15],使用Im表示第m台智能移动设备需要计算的数据量,使用一个常数α来表示所有计算数据的复杂性。由于模型中会将部分数据分流到服务器去计算,因此使用λm表示第m台智能移动设备在本地计算的数据量占总数据量的比例,其取值范围为[0,1]。根据以上关系,可以得到智能移动设备的工作时长计算公式如下:

单台智能移动设备的计算能耗根据公式(2)~(4)化简之后如下所示:

可见单台智能移动设备的计算能耗与智能移动设备芯片结构,智能移动设备的计算速度,需要计算的数据量和数据的复杂性有关。假设每台智能移动设备的电池容量有限,用ELmax表示每台智能移动设备能够用于计算的最大能耗,因此每台移动设备在处理数据所消耗的能源需满足:

与智能移动设备本地的计算能耗类似,边缘服务器的计算能耗也是通过边缘服务器的功率P和计算时间tCm的乘积计算得来,经相同的推导和化简后如公式(7)所示。在公式(7)中,用ECm表示服务器处理第m台智能移动设备分流数据产生的计算能耗,而第m台智能移动设备会保留λm的数据量在本地计算,所以服务器需要处理的数据量是(1-λm)·Im。具体公式如下:
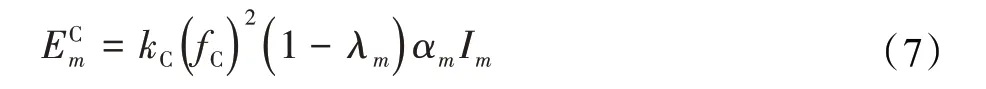
其中,kC是与边缘服务器芯片结构相关的一个常数,fC表示边缘服务器的计算速度这两个参数都与服务器的硬件条件相关。用ECmax表示服务器的最大能耗限制,因此,服务器在处理所有移动设备的数据产生的能耗要满足:
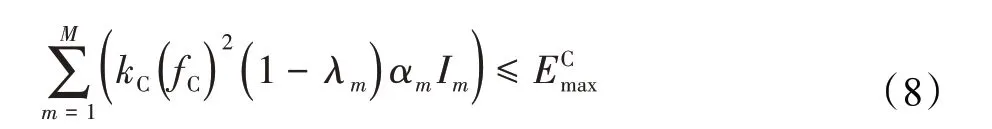
同时,对于边缘服务器接收M台智能移动设备传输过来的总数据量也有一定的限制,通过服务器最大CPU周期数Amax和服务器最大内存存储空间Gmax来表现,具体约束如下:
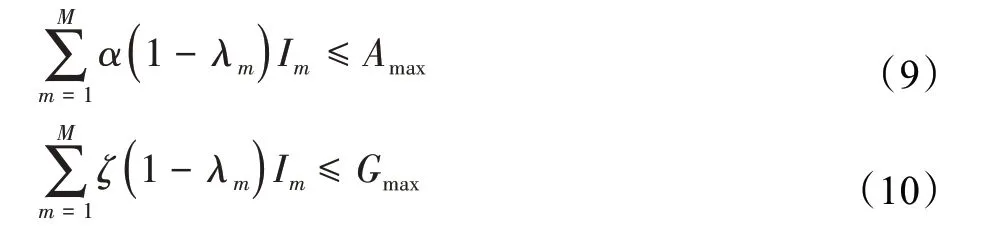
其中,α表示数据量的复杂性,而ζ表示每比特的数据所占用的内存空间。
对于第m台智能移动设备在传输数据到服务器的过程中的数据传输能耗ηm计算公式如下:
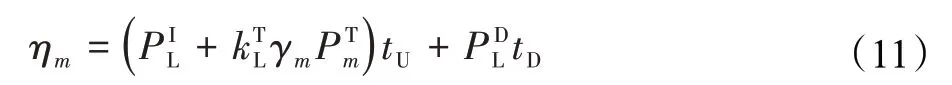
这个公式求和的两个部分分别代表数据传输中的上行链路能耗和下行链路能耗。其中,PIL表示智能移动设备的闲置功率,kTL表示智能移动设备传输数据的增强系数,PTm表示智能移动设备传输数据的功率,PDL表示智能移动设备下载数据的功率,下标L代表这些参数跟本地智能移动设备相关。
γm表示第m台智能移动设备在每条传输通道上所占用的带宽比例,其取值范围为[0,1],为确保最大限度地利用带宽,γm需要满足:

tU表示智能移动设备上传数据所需要的时间,tD表示数据从服务器传回智能移动设备的时间。tU、tD分别通过以下公式计算:


其中,RUm和RDm分别表示上行链路的和下行链路的信道传输速率,β1、β2分别表示在上传和下载数据过程中的额外开销。
数据传输能耗与传输时间有关,而数据传输时间跟信道传输速率相关。信道传输速率与数据占用的信道带宽W,数据传输功率PT和噪声干扰功率N0相关。在数据传输过程中存在干扰而导致信道衰弱现象,假设该模型的数据传输信道为瑞利衰落信道。根据文献[14],上行链路和下行链路的传输分别在不同的频率上进行。数据传输之间的路径损耗用(dm)-v表示,dm表示第m台智能移动设备到服务器的距离,v则表示路径衰减指数。h1、h2分别表示上行链路和下行链路的信道衰减系数。因此,链路的信道传输速率为通道数量S,传输带宽占比γm,链路带宽W,与数据传输功率衰减和噪声干扰有关的对数函数的乘积。上行链路的速率RUm和下行链路的速率RDm的计算公式为:
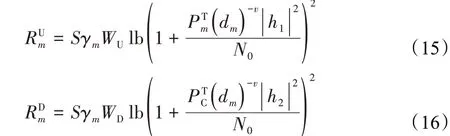
其中,S表示通道数量。WU和WD分别表示上行链路和下行链路的带宽。PTC表示服务器的传输数据的功率,N0表示高斯白噪声的功率。以上这些参数的取值都与对应的物理网络设备有关。
智能移动设备将部分数据分流给服务器完成计算的时间tC的计算如公式(17),该时间包括数据上传时间tU、数据下载时间tD和服务器处理第m台智能移动设备数据的时间tCm这三部分。

其中,上传数据时间tU和数据传回时间tD由公式(14)和(15)计算得到,而服务器处理数据的时间tCm与需要处理的数据量有关,具体计算公式如下:
大多数智能移动设备上的应用程序都有相应的延迟需求,最大完成时间包含两个方面,一方面是智能移动设备本地计算的时间tLm,由公式(4)计算得到,另一方面就是智能移动设备将部分数据卸载到服务器完成计算的时间tC。由于这两方面的计算是并行进行的,花费时间较多的那部分时间视为该计算任务的最终完成时间,因此该计算任务的最终完成时间需要满足:

其中,Lmax表示应用程序的延迟限制,即智能移动设备处理数据的最大完成时间。
2 基于分层学习的粒子群算法
粒子群算法因为其结构简单,收敛速度快等特点,受到国内外大量的研究,并应用到与各种实际问题中[16-17]。但是在解决复杂的约束问题时,粒子群算法存在容易陷入局部最优和缺失种群多样性等问题。因此,本文采用了分层学习的策略来对传统的粒子群算法进行改进,提出了利用基于分层学习的粒子群算法(levelbased learning swarm optimizer,LLSO),来提高PSO面对复杂优化问题时的全局搜索能力和种群多样性。
2.1 优化目标函数
本文的优化目标是最小化如公式(1)所示的所有本地设备的计算能耗,数据传输能耗和边缘服务器计算能耗的总和。由于同时还需要满足各种约束,如延迟约束,服务器存储约束,移动设备和服务器最大能耗约束以及传输网络的带宽约束,本文将所有的约束条件转化成对应的惩罚函数,因此优化目标是最小化总能耗和惩罚函数值的和,即:

其中,Ω表示所有惩罚函数值的总和,N为正整数,表示惩罚函数的权重,x代表问题的解。
惩罚函数Ω的计算方式如下:
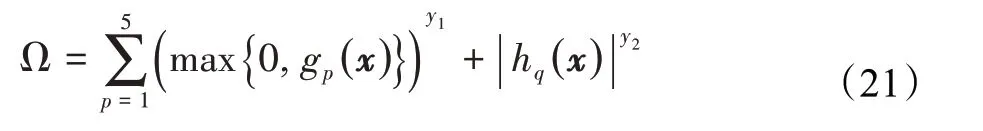
其中,y1、y2为指数常量,分别取值为2和1。gp(x)表示不等式约束的惩罚函数,p=1,2,…,5。hq表示等式约束的惩罚函数,具体公式如下:
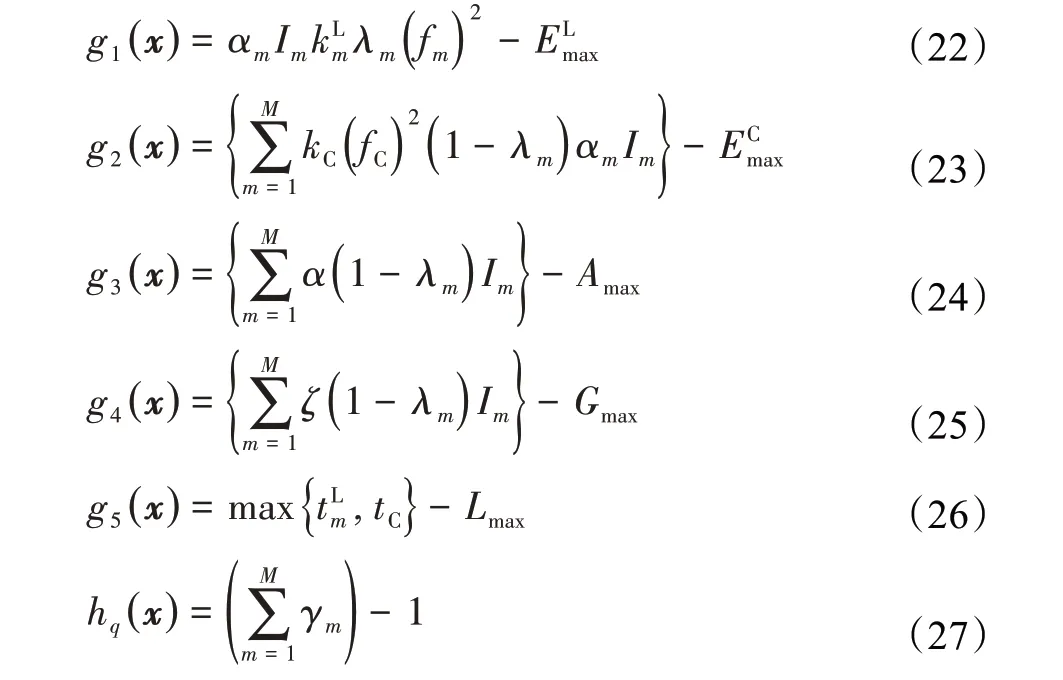
公式(22)到(27)分别是由移动设备最大能耗约束(6),服务器最大能耗约束(8),服务器CPU计算周期约束(9),服务器存储约束(10),延迟约束(19)和带宽约束(12)转化的各类惩罚函数。对于不等式约束,如果差值小于0,说明没有违反约束情况,惩罚值设为0,若差值大于0,说明违反了约束条件,将差值设为惩罚值。对于等式约束,差值不等于0表明违反约束,并用差值的绝对值表示惩罚值。
2.2 个体编码
LLSO算法的解向量x表示当前所有智能移动设备的资源分配情况,由智能移动设备相关的四个参数构成:智能移动设备的计算速度fm,智能移动设备下载数据的功耗PTm,计算数据卸载百分比λm和剩余网络带宽占比μm。假设智能移动设备的数量为M,向量x的长度是4M,其中第1到M的元素存放每台智能移动设备的计算速度fm,接下来的M个元素存放智能移动设备的功耗PTm,接着存放M个分流百分比λm,最后的M个位置存放 参 数 μm,最 终 向 量x的 编 码 方 式 如 下x=(f1,f2,…fM,PT1,PT2,…,PTM,λ1,λ2,…,λM,μ1,μ2,…,μM)。算法通过不断迭代优化,调整设备的计算功率参数,数据卸载比例以及传输网络带宽比例,最终输出的结果就是能耗最低的资源分配方式。同时LLSO算法中每个粒子会维护一个速度向量v。速度向量v是保存每个粒子的速度,表示资源分配变化的范围,向量v的长度也是4M,分别存放着每台智能移动设备不同参数对应的不同速度值。
2.3 算法流程
在算法开始运行前会先进行初始化粒子操作,在四个参数不同的取值范围内随机生成一个浮点数。四个优化参数对应取值范围为fm∈[0,fmax],PTm∈[0,Pmax],λm∈[0,1],μm∈[0,1]。其中fmax表示智能移动设备的最快计算速度,Pmax表示智能移动设备最大传输功率。在初始化完成后,会先将参数μ换算成每台智能移动设备真实的带宽占比γ,计算方法如下,其中γ1=μ1:
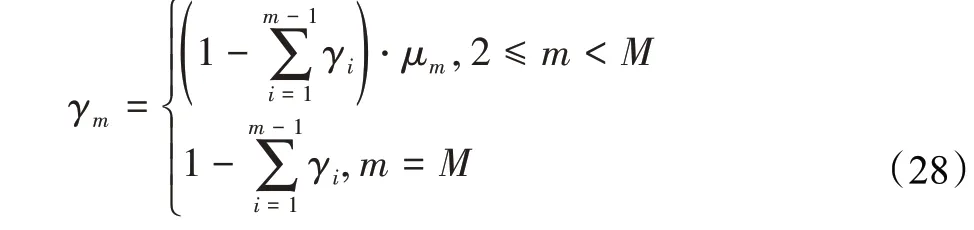
换算完成后,还会对参数λ和参数γ之间的数据关系进行一个判断:如果当γ的值为0时,说明某个智能移动设备没有使用带宽通道去传输数据给服务器计算,表示所有数据必须在智能移动设备上计算,因此需要将对应的参数λ的值修改为1。最后更新粒子群的全局最优粒子。
在进化的过程中,不同适应度的粒子在局部寻优和全局寻优中有着不同的作用[16],因此将它们区别开来,根据适应度的不同划分不同的层次。分层学习策略先将种群按照适应度值的大小进行排序并进行分层操作,层数较低的粒子在进行更新操作时,学习的对象是层数较高的任意一个粒子。这种方法促使粒子向比自身更优的粒子学习,同时也保留了搜索的多样性。
假设种群的数量为NP(number of particles),将该种群按照适应度的大小分为NH(number of height)层,每一层用Hi(1≤i≤NH)表示,那么划分到同一层的粒子数量为HS(height size),并且HS=NP/NH。如图2所示,将初始化之后的种群按照目标函数值从小到大进行排序,然后按顺序每HS个粒子划分为一层,其中前HS个粒子划分为第一层H1,最后HS个粒子划分到最后一层HNH。
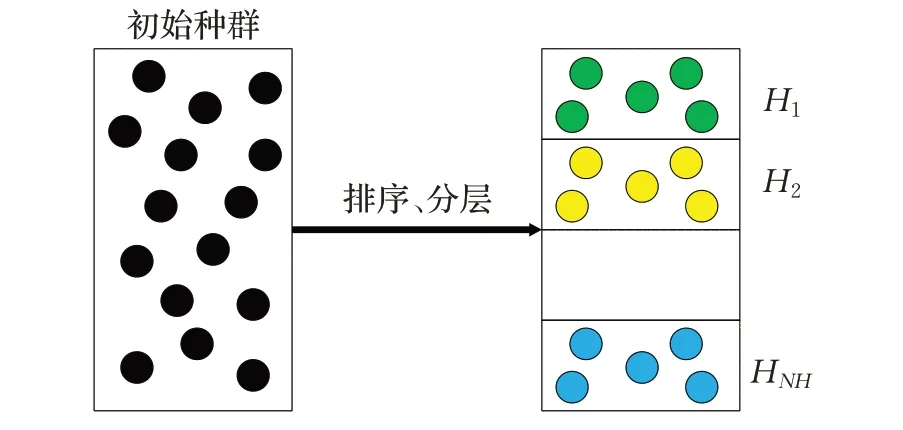
图2 分层学习策略Fig.2 Strategy of level-based learning
在分层操作完成后进行算法的个体更新操作,与传统的PSO算法按下标顺序更新粒子不同,LLSO算法是从层级最低,即位于HNH层的粒子开始更新,再更新层级较高的粒子。在更新操作中,假设位于第i层中的第j个粒子xi,j,1 其中,r1、r2、r3都是在[0,1]中随机生成的随机数,而ϕ是控制参数,主要影响粒子xl2,k2的更新效果,其取值范围在[0,1]。 LLSO算法的伪代码如算法1所示。第1行初始化粒子群,在参数的取值范围内随机生成浮点数,第2行根据公式(20)计算每个粒子的适应度值,并初始化全局最优粒子。第4到15行是算法的迭代优化过程:第5行进行分层操作,第6到13行对每个粒子进行更新操作,对于每个待更新的粒子,首先选取层级较高的两个粒子,再根据公式(29)、(30)更新该粒子的速度信息和位置信息,最后再更新粒子的适应度值。第14行在更新完粒子后重新比较每个粒子的适应度值,更新全局最优粒子。第16行输出最终的优化结果。 算法1基于分层学习的粒子群算法 输入:种群大小NP,分层数量NH,控制参数ϕ,最大适应度评估次数MAX_FES 输出:全局最优个体 1.初始化粒子群,计算每层划分的个体数量,令fes=0 2.计算种群中所有粒子的适应度值,初始化全局最优粒子 3.fes+=NP; 4.while fes 5. 按照粒子适应度值大小进行分层操作; 6. For i=NH to 2 do 7. For j=1 to HS do 8. 随机选取层级较高的粒子xl1,k1,xl2,k2作为进化榜样; 9. 根据公式(29)、(30)更新粒子xi,j的速度信息和位置信息; 10. 计算粒子新的适应度值; 11. End For 12.fes+=HS; 13. End For 14. 更新全局最优粒子; 15.End while 16.输出全局最优个体 为了验证LLSO算法在解决边缘计算资源调度问题上的性能,本文将使用LLSO算法用于移动设备的能耗优化问题。实验会测试LLSO算法对于不同移动设备数量情况下的优化性能,因此本次实验中智能移动设备的数量的取值范围为[5,10]。而本次实验的模型参数,即目标函数中与智能移动设备和服务器相关的常数参数,根据文献[18-19],做出以下设置,如表1所示。 表1 目标函数参数默认值Table 1 Default values of parameters of objective function LLSO中引入了两个参数,分层的数量NH和控制参数ϕ。NH大小影响进化过程中种群的多样性,控制参数影响着粒子xl2,k2在进化过程中的影响力,而该粒子具有更多的全局寻优潜力。因此这两个参数会影响LLSO算法的整体表现,根据文献[17],将这两个参数设置为NH=4、ϕ=0.4。种群数量NP=100。 同时为了验证LLSO算法在优化结果和优化速度上的优势,本文选择其他具有代表性的启发式算法对同一个问题同时进行优化,并比较它们的优化结果。选取的算法如下:模拟退火算法(SA)[20]、遗传算法(GA)[21]、粒子群算法(PSO)[22-23],基于模拟退火的粒子群算法(SA-based PSO,SAPSO)[24]和基于遗传模拟退火的粒子群算法(genetic simulated-annealing-based particle swarm optimization,GSP)[25]。对比算法的参数设置如下:根据文献[25],GSP算法中的初始温度参数设为108,降温速率为0.95,变异概率为0.01,惯性权重的取值范围为[0.4,0.95],加速因子1.496,学习因子0.5。SA算法的初始温度为108,降温速率为0.95。GA算法中的交叉概率为0.8,变异概率为0.01。根据文献[26],PSO算法中加速因子c1为1.85,加速因子c2为2,惯性权重的取值范围为[0.38,0.99]。 表2的数据是六种算法在不同数量的移动设备的情况下独立运行100次的能耗优化的结果,每种算法在目标函数评价达到200 000次时停止优化,并且用可行解概率来表示每种算法在100次独立运行中得到可行解次数百分比,即可行解惩罚值为0的结果。从表2的结果可以看出,在100次独立运行中,本文提出LLSO算法的能耗优化结果比其他五种算法的优化结果较好,并且在所有不同移动设备数量情况下LLSO算法的可行解概率都能达到100%。当移动设备数量较少时,如M=5和M=6时,所有算法都能求出可行解,其中GA和GSP算法的能耗平均值与LLSO算法比较接近,但LLSO算法的能耗优化结果最低。当移动设备的数量增多时,如M=9和M=10时,SA和PSO这两种算法的可行解概率都低于20%,说明这两种算法在移动设备数量较多的优化模型中已经无法适用,GSP、GA和SAPSO四种算法的可行解概率低于90%,而LLSO算法的可行解概率仍是100%。 表2 六种算法在不同移动设备数量的优化结果Table 2 Optimization results of six algorithms in different number mobile devices 图3展示的是六种算法在六种不同移动设备的情况下的能耗优化收敛趋势图,其收敛曲线展示的是100次独立运行的平均值收敛情况。从图中可以看出LLSO算法在所有情况下的平均优化结果都优于其他五种算法,在20 000次评价次数的时候已经接近收敛。GSP算法与LLSO的收敛趋势比较接近,但GSP算法的优化结果没有LLSO算法好。GA算法的收敛速度最快,在第5 000次迭代的时候就接近收敛,收敛结果与GSP算法相同。当移动设备数量较少时,GA算法的优化结果与LLSO算法的优化结果相近,相差不到0.1,但当移动设备数量增多时,优化结果的差距逐渐增大,当M=10时,LLSO算法的优化结果比GA算法提高10%左右。SA、PSO和SAPSO算法与LLSO算法相比优化结果较差,并且在M大于7时这三种算法的收敛曲线出现波动,说明这三种算法在移动设备数量较多时无法优化出满足约束条件的结果,导致能耗值收敛曲线出现上升的现象。 图3 六种算法能耗值优化收敛图Fig.3 Energy consumption optimization convergence diagram of six algorithms 图4展示的是六种算法在不同移动设备情况下100次独立运行的能耗优化结果的分布情况。从图中可以看出,LLSO算法的结果最好,优化结果分布最为集中,说明LLSO算法的表现稳定,并且能耗平均值和中位数都比其他四种算法较低。GA算法和GSP算法的结果分布情况相近。而SA、PSO和SAPSO算法的优化结果分布较差,其中PSO算法在不同数量移动设备情况的优化结果的分布范围比其他算法的大,可以看出PSO算法的优化结果不稳定。 图4 六种算法优化结果分布对比Fig.4 Comparison of optimization results distribution of six algorithms 随着物联网行业的发展,智能移动设备越来越普及,但是移动设备因其便携性和移动性的特点,使得移动设备无法满足对于计算资源要求较高的应用程序。而边缘计算技术为解决这一问题提供了解决方案,通过将部分任务分给边缘服务器完成来满足应用服务的计算需求。而如何制定计算卸载决策,合理分配资源,成为边缘计算资源调度中一个挑战。因此本文提出了一种移动设备计算卸载模型,通过调整计算卸载的比例和计算资源的分配,使得所有移动设备和边缘服务器消耗的总能量达到最小,并使用基于分层学习的粒子群算法来优化这一问题,并通过对比实验证明该算法比其他优化算法获得了具有更低的能耗的解。本文的未来工作包括设计新的搜索模式用于算法求解大规模问题,提高移动设备数量较多时算法得出可行解的能力。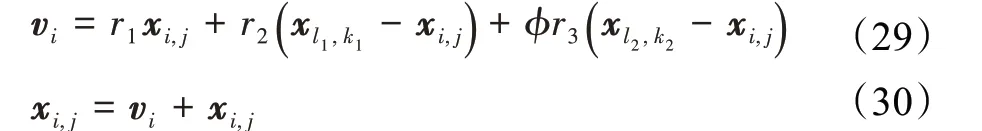
3 实验
3.1 实验介绍和参数设计
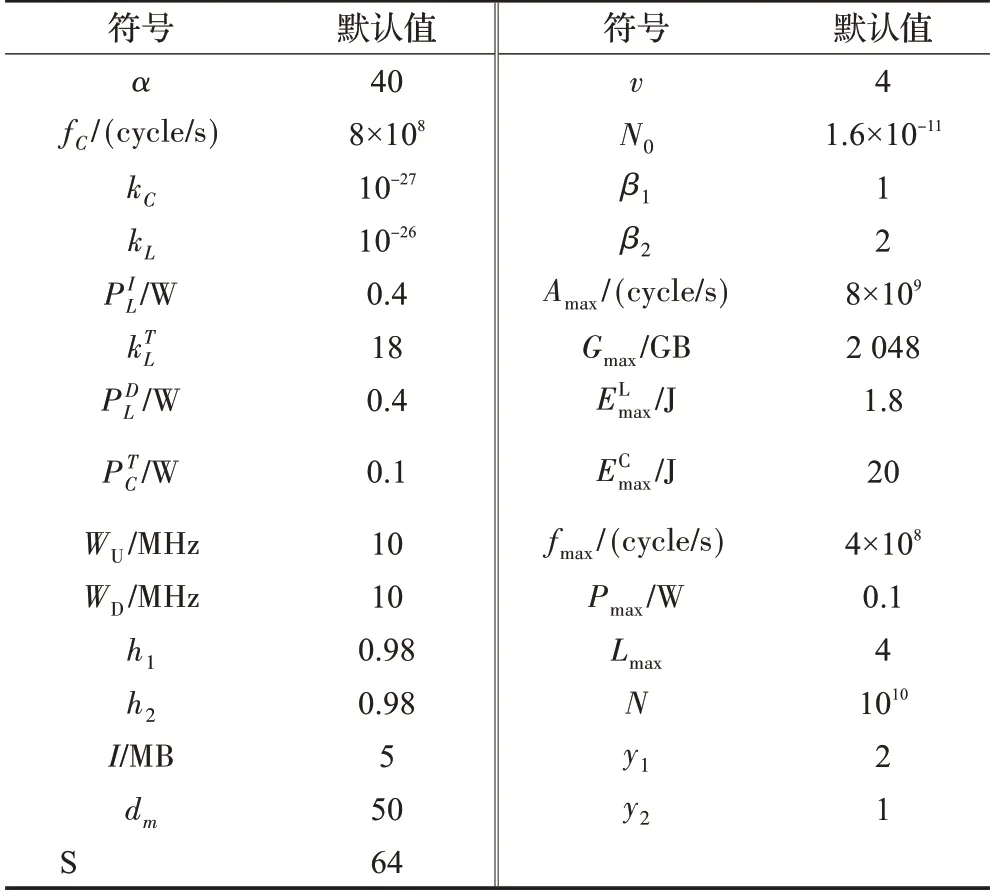
3.2 实验结果
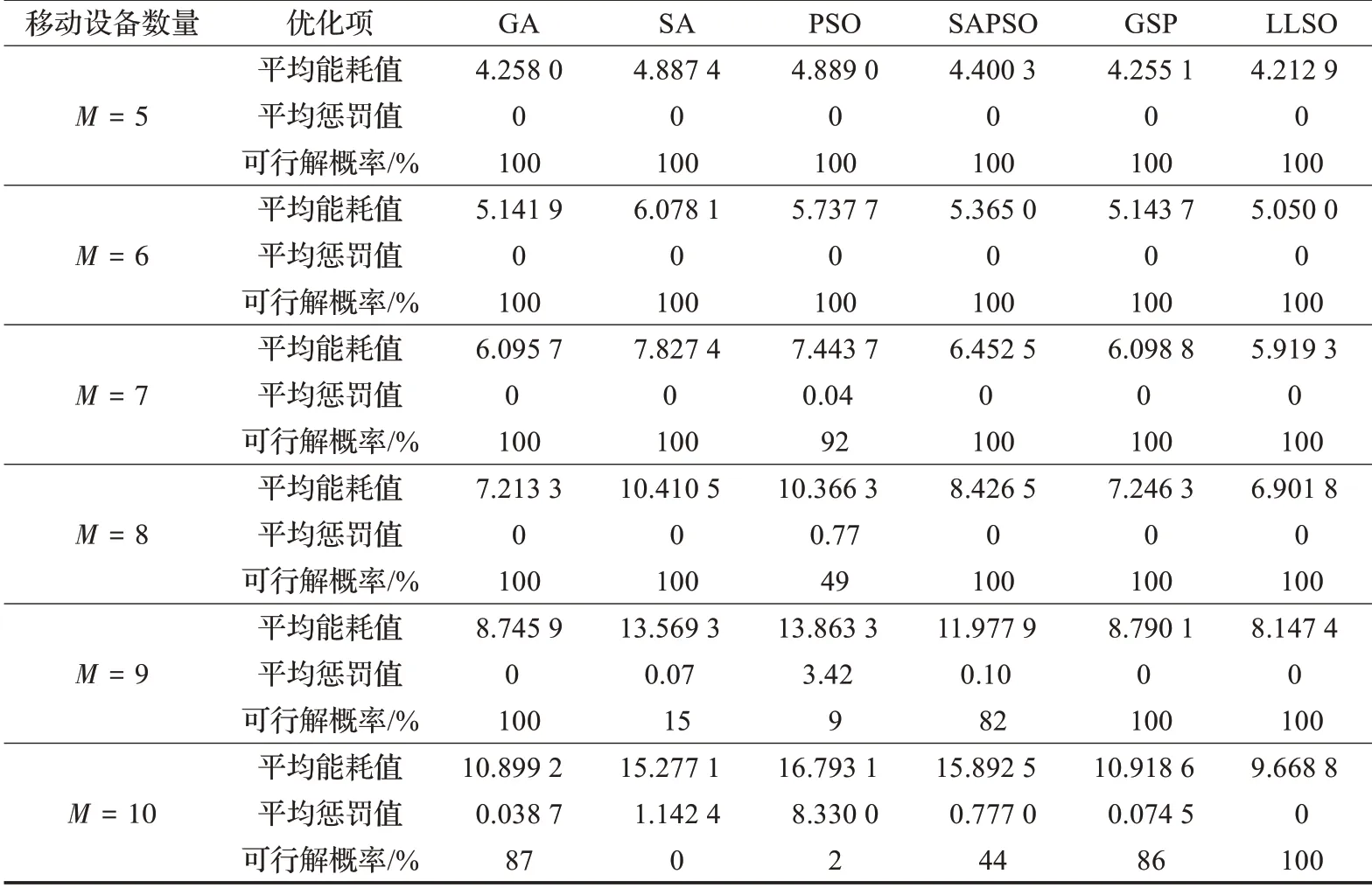
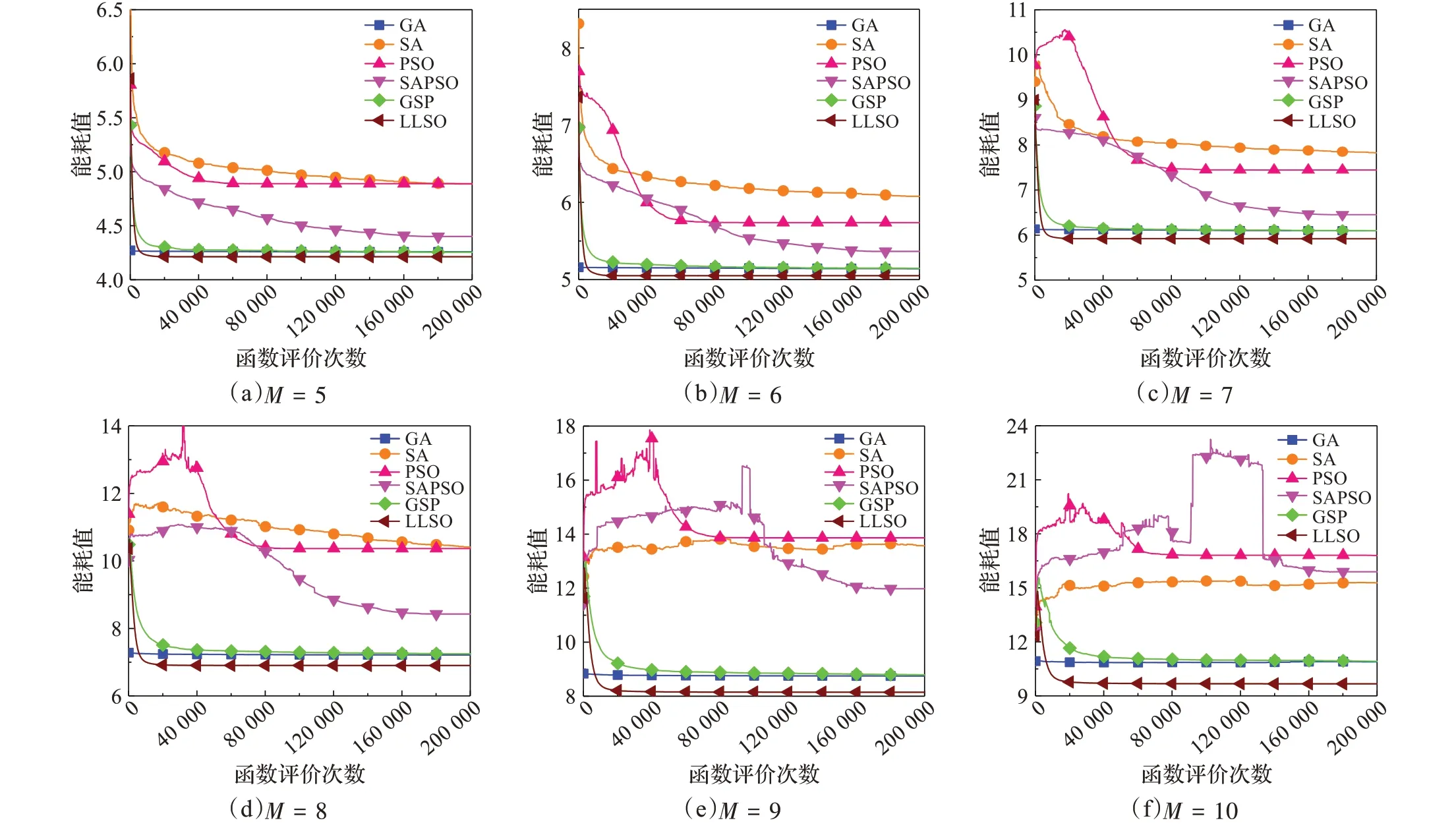
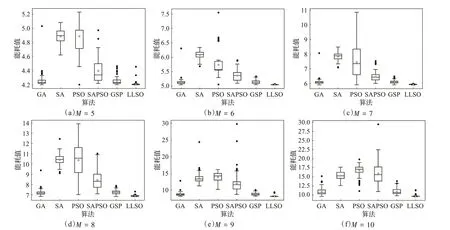
4 结束语

