三阶非线性边值问题正解的存在性

张丽，闫善文

（黑龙江八一农垦大学理学院，大庆 163319）

1 问题与主要定理

在泛函分析理论以及实际问题的推动下，微分方程边值问题的研究发展十分迅速。越来越多的学者利用一些著名的不动点定理和上下解方法等理论工具,研究微分方程边值问题正解的存在性和多重性[1-6]，并且随着研究的深入，出现了许多研究方向如：奇异边值问题[7-12]，流体问题中的边值问题[13-16]，带算子的微分方程边值问题[17-18]，脉冲边值问题[19-20]等。

研究如下形式的三阶非线性边值问题

这里参数ρ＞0。

首先，给出正解定义。

定义1称函数u（t）为边值问题（1）的一个正解，如果它满足

其次，假设如下：

（H4）对几乎所有的t∈（0，1），f(t，u)关于u≥0单调非增。

最后，在上述假设条件下，得到本文的主要结果。

定理1假设（H1），（H2）或（H1），（H3）成立，则边值问题（1）至少存在一个正解。

定理2假设（H1），（H3），（H4）成立，则边值问题（1）存在唯一的正解。

在假设（H1），（H3），（H4）之下，f(t，u)可以有适当的奇性，例如f(t，u)=满足（H1），（H3），（H4）。

2 预备工作

设C[0，1]是[0，1]上全体连续函数构成的Banach空间，记

容易知道（2）等价于下述的积分方程

这里给出Green函数G（t，s）形式

若ν（t）是（3）的一个正解，令u（t）=Jν（t），则容易导出u（t）是（1）的一个正解。

引理1∀s，t∊[0，1]有

证明 利用Taylor公式易知

因此

在C[0，1]中定义锥K为：

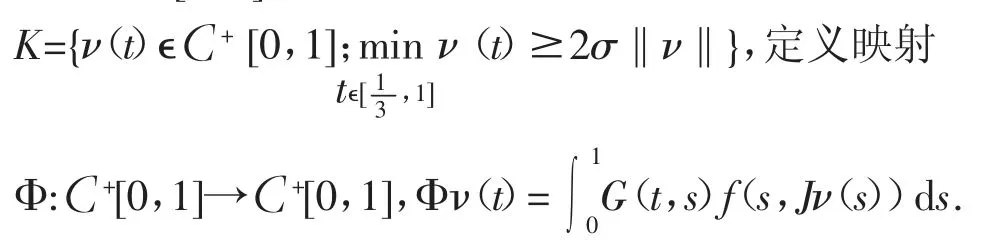
引理2 Φ：K→K全连续。

证明∀ν∊K，由引理1知

于是

因此Φν∊K，即Φ（K）⊂K。

另外，记D是C+[0，1]中的任何有界集，Φ（D）一致有界且等度连续，由Ascoli-Arzela定理的应用可知，Φ（D）是相对紧的，又Φ是连续算子，故Φ：K→K是全连续的。

为寻找Φ在K中的非零不动点，需要下述的锥不动点定理，参见[21]。

引理3（锥不动点定理）设E是Banach空间，K是E中的锥，Φ：K→K是全连续算子，记Kr={u∊K；‖u‖＜r}，

（i）如果对任何u∊∂Kr，及任何0＜λ≤1都有λΦu≠u，则i（Φ，Kr，K）=1；

3 定理1的证明

假设（H1），（H2）成立.由（H2）知可选择ε∊（0，μσ）及r＞0，使当0≤u≤r时有

f（t，u）≤（μσ-ε）u.

下证∀ν∊∂Kr，0＜λ≤1有λΦν≠ν.若不然，则存在ν0∊∂Kr及0＜λ0≤1使λ0Φν0=ν0.由映射Φ的定义知ν0（t）满足

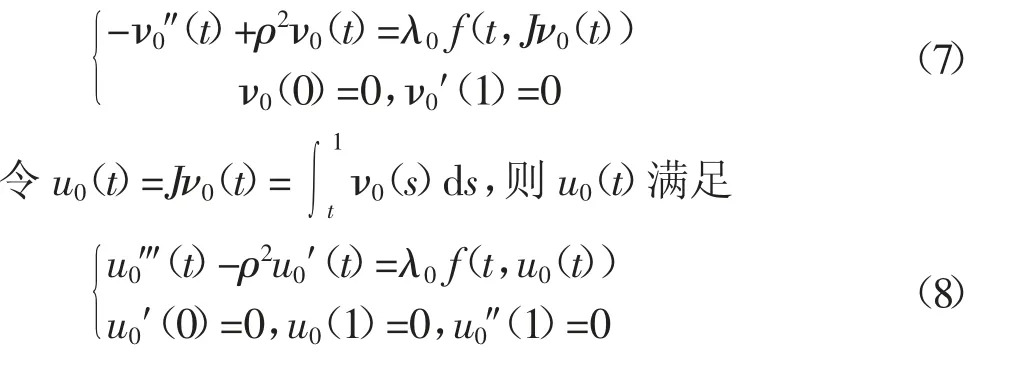
由于

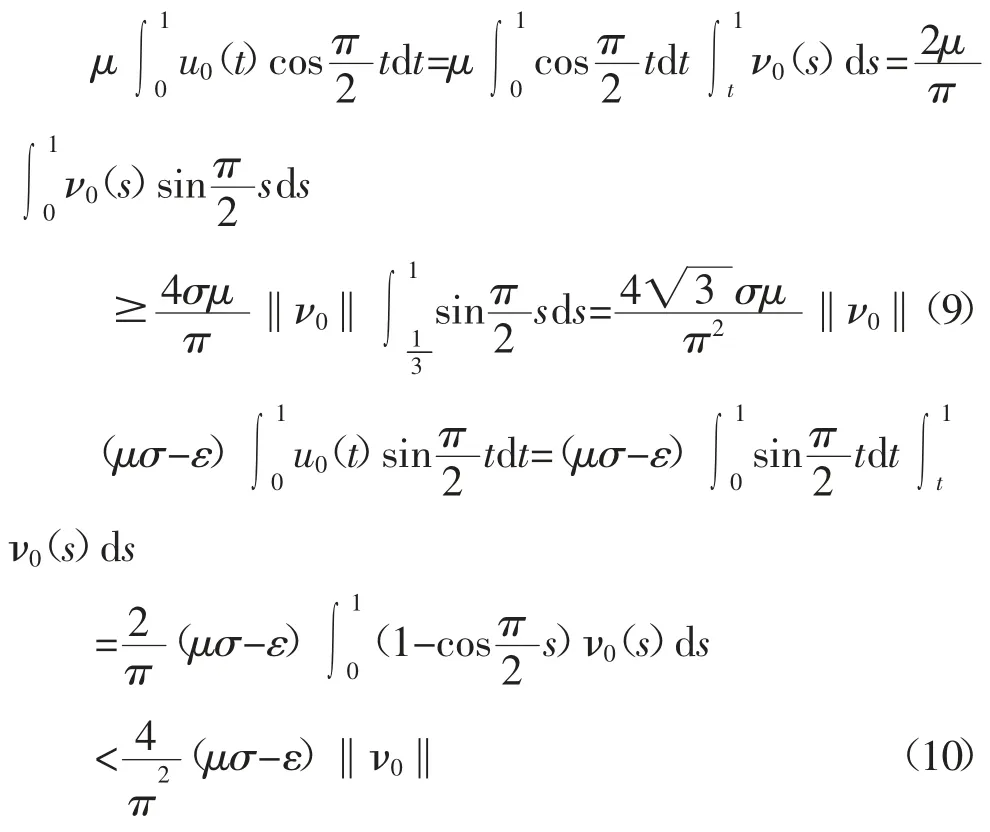
因此有

即有

这是矛盾的，根据引理3知i（Φ，Kr，K）=1.

再由（H2）可知，存在ε＞0及H＞0，使当u≥H时

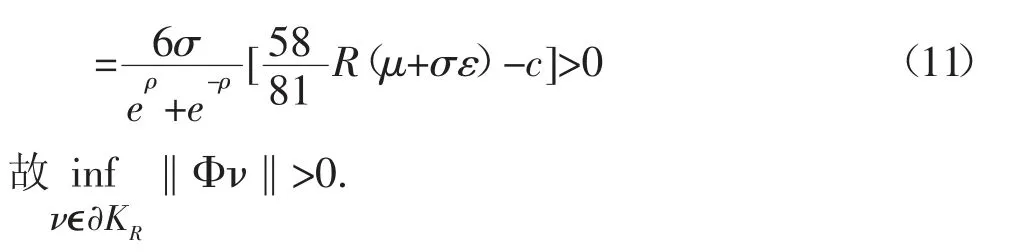
下证∀ν∈∂KR，λ≥1都有λΦν≠ν.若不然，则存在ν0∈∂KR，λ0≥1，使λ0Φν0=ν0，即ν0（t）满足（7）式，再令u0乘以（8）式两边并在[0，1]上积分得到

另外有

于是有

i（Φ，KR，K）=0.

根据不动点指数的可加性知

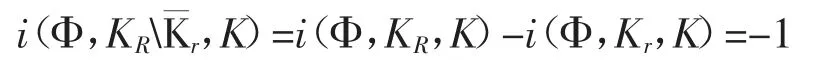
假设（H1），（H3）成立。由（H3）知存在ε＞0及r＞0，使当0≤u≤r时有，因Jν于是，与（11）式的计算相类似可得故

现证∀ν∈∂Kr，λ≥1，有λΦν≠ν.若不然，则存在ν0∊∂Kr及λ0≥1，使λ0Φν0=ν0。于是ν0（t）满足（7）式，令u0（t）=Jν0（t），则u0（t）满足（8）式。以乘（8）式两边并在[0，1]上积分得到

与（12），（13）两式的计算类似可得

因此有

即μ＞μ+σε，结果矛盾。故由引理3知i（Φ，Kr，K）=0。

再由（H3）可知，存在ε∊（0，μσ）及H＞0，使当u≥H时有f（t，u）≤（μσ-ε）u，令则有f（t，u）≤（μσ-ε）u+c，∀u≥0。

与（9），（10）两式的计算类似可得

因此有

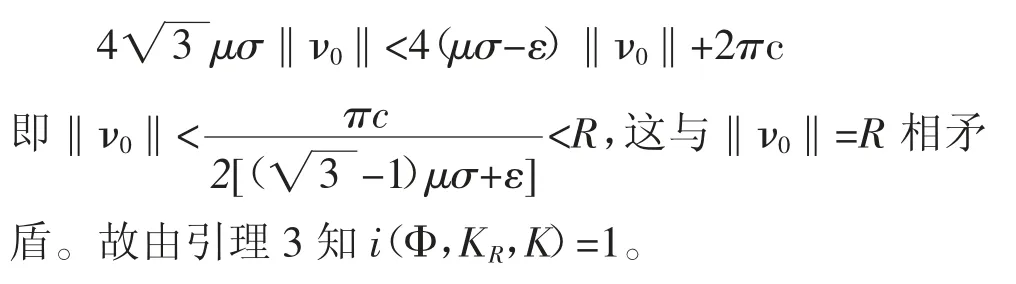
再由不动点指数的可加性知

4 定理2的证明

设u1（t）和u2（t）都是边值问题（1），（2）的正解，令u（t）=u1（t）-u2（t），则u（t）满足

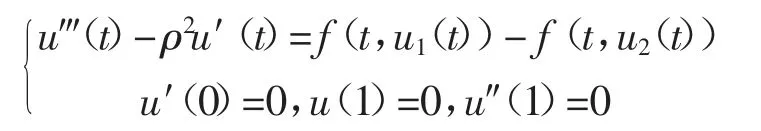
现证明在区间[0，1]上ν（t）=0。否则由ν（0）=0知，在（0，1]上ν（t）≠0。

若ν（1）＜0，由ν（0）=0知存在0≤ɑ＜1，使在（ɑ，1]上ν（t）＜0，ν（ɑ）=0，于是在[ɑ，1]上ν（t）满足

由此可得

此处

由于在（ɑ，1]上ν（t）=ν1（t）-ν2（t）＜0，有Jν1（t）-Jν2

这与ν（t）＜0相矛盾，故ν（1）=0。

若有t0∊（0，1）使ν（t0）＜0，则存在0≤ɑ＜t0＜b≤1，使在（ɑ，b）内ν（t）＜0，ν（ɑ）=0，ν（b）=0。我们断言在[b，1]上ν（t）=0。若不然，则存在t1∊（b，1）使ν（t1）≠0可设ν（t1）＜0，由于ν（b）=ν（1）=0，于是存在区间[c，d]⊂（b，1），使在（c，d）内ν（t）＜0，ν（c）=0，ν（d）=0，不妨设c=b，d=1于是在[b，1]上ν（t）满足

由此可得

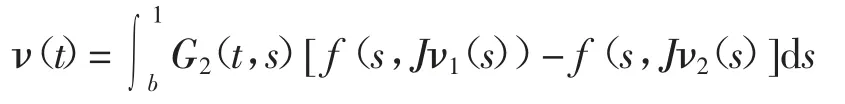
这里

由于在（b，1）内，ν（t）=ν1（t）-ν2（t）＜0，故Jν1（t）-

这与在（b，1）内ν（t）＜0相矛盾。

综上可知，在[ɑ，b]上ν（t）满足

因在[b，1]上ν（t）=0，故

因此f（t，Jν1）-f（t，Jν2）≥0，t∊[ɑ，b]。于是可导出

其中

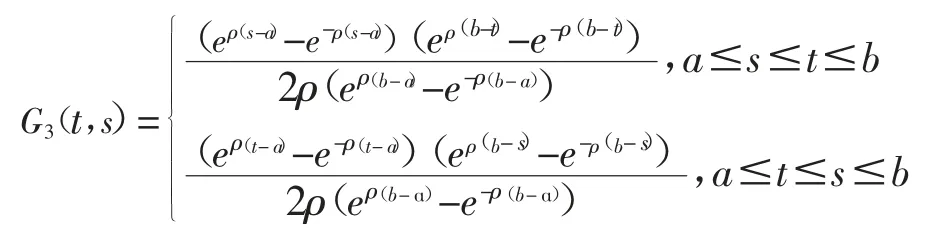
这与在（ɑ，b）内ν（t）＜0相矛盾。

5 结论

研究了含参数三阶非线性边值问题u‴（t）-ρ2u′（t）=f（t，u（t）），（0＜t＜1，ρ＞0）；u′（0）=0，u（1）=0，u″（1）=0正解存在性。首先给出了该问题正解存在的充分条件；其次构造了此问题的Green函数，利用Green函数的性质，在适当的空间上定义映射，将积分方程转化为算子方程，进而将该边值问题转化为等价的积分方程；最后利用锥不动点定理证明正解的存在性。