美英早期几何教科书中与圆有关的角
刘梦哲 汪晓勤
(华东师范大学教师教育学院 200062)
1 引言
圆心角、圆周角和弦切角的概念及相关定理是“圆”一章的重要内容,深刻揭示了圆中的弧、弦、角之间的关系.《义务教育数学课程标准(2022年版)》指出,要求学生理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论[1].
在已有的教学设计中,张安军基于学生所学习过的垂径定理,从圆的轴对称性引出圆的旋转对称性,从而探究弧、弦、圆心角之间的关系[2].高建成基于学科大概念对圆周角的教学进行重构,由圆心角类比圆周角,由此形成定义,从分类讨论中提炼模型,由此证明定理[3].林秋华在圆周角定义的基础上,得到弦切角的定义,并从动态的角度引导学生发现、归纳得到弦切角定理[4].可见,在实际教学中,教师会让学生通过观察,给出圆心角、圆周角和弦切角的定义;通过探究圆的旋转不变性,发现弧、弦、圆心角之间的关系;通过分类讨论并利用三角形外角定理,证明圆周角定理.
HPM视角下的数学教学对于学生理解知识、掌握技能以及增进对数学过程与方法的理解起到了十分重要的作用[5].然而,手头无史料却成为阻碍教师在教学过程中开展HPM实践的一大原因.教师对圆心角、圆周角和弦切角的历史知之甚少,相关的HPM课例付之阙如.鉴于此,本文聚焦圆心角、圆周角和弦切角,对美英早期几何教科书进行考察,希望从中获得恰当的教学素材和思想启迪,为今后的课例研究提供参考.
2 早期教科书的选取
本文选取1829—1948年间出版的87种美英早期几何教科书作为研究对象,以20年为一个时间段进行划分,其出版时间分布情况如图1所示.其中,对于同一作者再版的教科书,若内容无显著变化,则选取最早的版本,若内容有显著变化,则将其视为不同的教科书.

图1 87种美英早期几何教科书的出版时间分布
关于圆心角、圆周角和弦切角的内容主要位于“圆”“直线和圆”“角度测量”“圆和正多边形”等章节中.其中,圆心角和圆周角的概念大多出现在“圆”一章的“定义”一节,圆心角定理大多出现在“圆心角”一节,而圆周角定理和弦切角定理大多出现在“角度测量”一节.
3 圆心角的概念
在58种给出圆心角概念的教科书中,定义方法可以分为邻边定义、静态定义和顶点定义3类,具体分类情况见表1.
4 圆心角定理
所谓圆心角定理,即在同圆或等圆中,相等的圆心角所对的弧相等,相等的弧所对的圆心角相等.因此,证明圆心角定理需证明以下两个命题:
命题1 在同圆或等圆中,相等的圆心角所对的弧相等;
命题2 在同圆或等圆中,相等的弧所对的圆心角相等.
4.1 命题1的证明
·叠合法

图2 命题1的证明
·弧弦关系法

·比例法
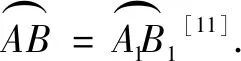
4.2 命题2的证明
·叠合法
类似于证明命题1的方法,通过平移和旋转使两扇形重合后同样可以证明命题2.有46种教科书采用了叠合法,其中27种选择从半径重合出发,14种选择从弧重合出发,5种仅提及使用这一方法.


·弧弦关系法
·反证法
通过假设在同圆或等圆中,等弧所对圆心角不相等,再利用命题1中的结论即可导出矛盾.有3种教科书采用了这一方法.


图3 利用反证法证明命题2
·比例法
有2种教科书采用这一方法.在同圆或等圆中,因为圆心角所对的弧相等,即两弧的比值为1,而圆心角的比值等于其所对弧长的比值,所以两弧所对圆心角也相等[11].
·圆周角法

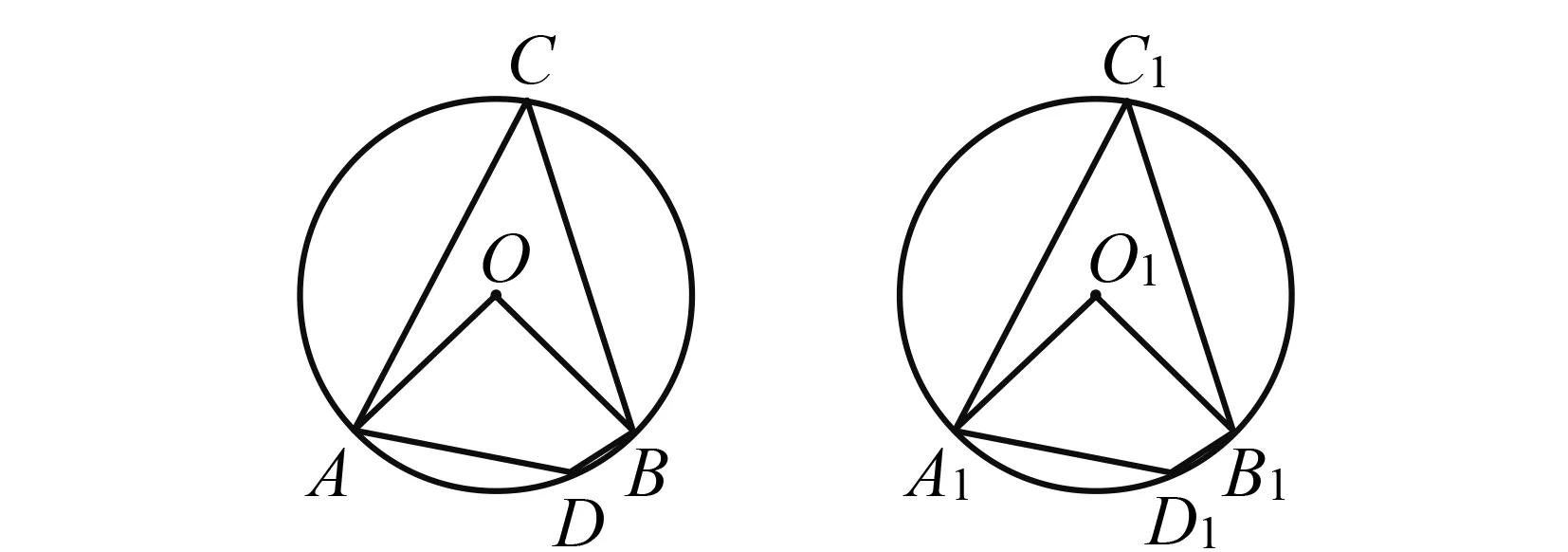
图4 利用圆周角法证明命题2
·逆定律法
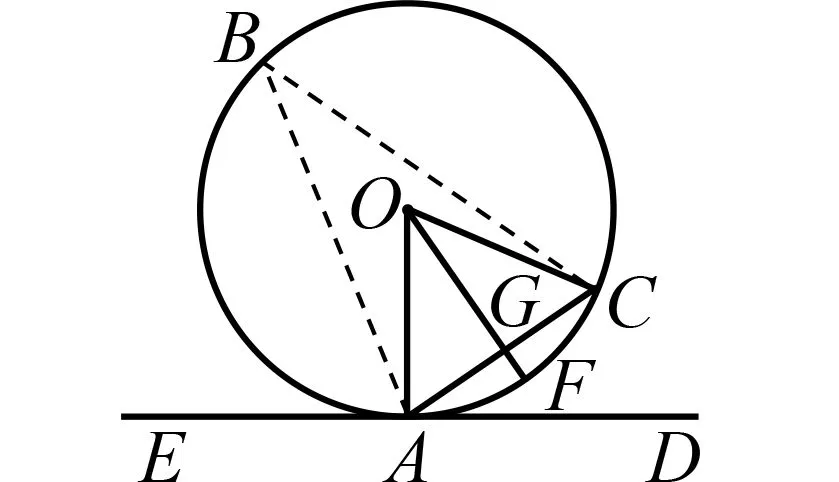
所谓逆定律(law of converse)是指:若A>B⟹X>Y,A=B⟹X=Y,A 在87种美英早期教科书中,除5种没有给出圆周角概念外,其余82种教科书通常将圆周角称为an inscribed angle或an angle inscribed in a circle,并给出了详细解释.圆周角概念的定义方法可以分为静态定义、邻边定义和动态定义3类.表2是圆周角概念的定义分类情况. 表2 圆周角概念的定义分类 在87种美英早期教科书中,78种教科书将圆周角定理表述为:圆周角等于其所对弧的一半;9种教科书将其表述为:一条弧所对的圆周角等于这条弧所对圆心角的一半.后者与现行教科书给出的表述相一致.其中,证明上述定理的方法可以分为三角形外角法、平行线法以及弦切角法3类. 在给出圆周角定理证明过程的86种教科书中,有93%的教科书利用了三角形外角定理.如图5,在⊙O上任取一个圆周角∠BAC,于是可以分三种情况进行讨论,即圆心O在∠BAC的边上、内部以及外部[17]. 图5 利用三角形外角法证明圆周角定理 如图5(1),即圆心O在∠BAC的边AB上的情况.连结OC,因为OA=OC,所以∠BAC=∠C,于是,由三角形外角定理可知,∠BOC=∠BAC+∠C=2∠BAC.对于图5(2)的情况,因为∠BOD=2∠BAD,∠DOC=2∠DAC,故∠BOC=2∠BAC.同理,对于图5(3)的情况,也可得∠BOC=2∠BAC. 图6 利用平行线法证明圆周角定理 有3种教科书采用了平行线法,即过圆心作圆心角一边的平行线,进而完成证明.对于圆周角一边过圆心的情形,如图6,过圆心O作OE∥AC,于是∠BAC=∠BOE,∠C=∠COE.又因为OA=OC,所以∠BAC=∠C,于是∠BAC=∠BOE=∠COE,故∠BOC=2∠BAC.其他两种情形的论证同6.1节[18]. 图7 利用弦切角定理证明圆周角定理 另一种方法为Grund所采用.如图7(2),因为∠BOA=2∠BAE,∠COA=2∠CAD,2(∠BAE+∠BAC+∠CAD)=360°,故得∠BOC=360°-(∠BOA+∠COA)=360°-2(∠BAE+∠CAD)=2∠BAC.[11] 在87种美英早期教科书中,并没有直接给出弦切角的概念,而只是在弦切角定理中有所提及.其中,有54种教科书在定理或证明中将弦切角定义为由一条切线和一条过切点的弦所夹的角;有32种教科书将弦切角定义为由切线和弦所夹的角,但没有指出弦切角的顶点在圆周上,而是在图中指明弦切角;剩余1种教科书中没有弦切角定理. 相比于弦切角概念的单一表述,弦切角定理的证明方法则非常丰富.所谓弦切角定理,即弦切角的大小等于它所夹的弧所对圆心角的一半,等于它所夹的弧所对的圆周角.在84种给出弦切角定理证明的教科书中,证明方法可以分为圆周角法、平行线法、垂径定理法和动态法4类. 有超过半数的教科书在证明弦切角定理的时候,不约而同地用到了圆周角定理的3个推论,即 ①同弧或等弧所对的圆周角相等,②直径所对的圆周角是直角,③圆内接四边形的对角互补. 图8 利用圆周角法证明弦切角定理 图9 利用平行线法证明弦切角定理 图10 利用垂径定理法证明弦切角定理 图11 利用动态法证明弦切角定理 综上所述,在与圆有关的角这一主题上,美英早期教科书为我们呈现出圆心角、圆周角和弦切角的多种定义方式以及圆心角定理、圆周角定理和弦切角定理的多种证明方法,这些方式或方法为今日教学带来了诸多启示. 第一,在引入圆心角、圆周角和弦切角的概念时,可以先让学生尝试从这几个角的名字出发进行描述,随后向学生指出圆中这三个角的位置并让学生予以补充,最后教师对不同的定义方法进行总结和完善.这样循循善诱的教法,一方面给予了学生今后自学概念的方法,更重要的是让学生体会知识的发生过程,有助于构建知识之谐. 第二,在证明圆心角定理、圆周角定理以及弦切角定理时,教科书上单一的证明方法可能会束缚学生的思维,形成思维定势,这并不符合创新性人才培养的要求.教师可以引导学生一题多思、一题多解、一题多变,在掌握课本上的证明方法之后,开展小组探究活动,尝试使用不同的工具来证明这些定理.一方面,“头脑风暴”式的数学课堂有利于培养学生数学发现和创造能力,提高学生分析问题和解决问题的能力,最终开拓学生的思路,发展学生的智力.另一方面,学生在探究中能加深对于这几个定理的理解,在豁然开朗时体会到成功所带来的喜悦,有助于营造探究之乐. 第三,抽丝剥茧,深入挖掘定理证明背后的数学思想.例如,采用叠合法证明圆心角定理中的类比思想、利用三角形外角定理证明圆周角定理中的分类讨论思想、采用平行线法证明弦切角定理中的化归思想等,无疑是数学课堂上的宝贵思想养料.这一切不仅使原本枯燥的定理学习变得精彩纷呈,同时还有助于培养学生的数学抽象、逻辑推理、直观想象等核心素养,有助于彰显方法之美、实现能力之助. 第四,在介绍圆心角、圆周角和弦切角的概念及定理时,可以借助微视频,展示各国数学家探索这三类角的概念和有关定理的过程,追溯知识源流,呈现多元文化.与此同时,数学家对于数学真理的不懈追求与热爱,有助于激发学生学习数学的兴趣,体会数学背后的理性精神,最终达成德育之效.5 圆周角的概念

6 圆周角定理
6.1 三角形外角法

6.2 平行线法

6.3 弦切角法


7 弦切角及弦切角定理
7.1 圆周角法



7.2 平行线法

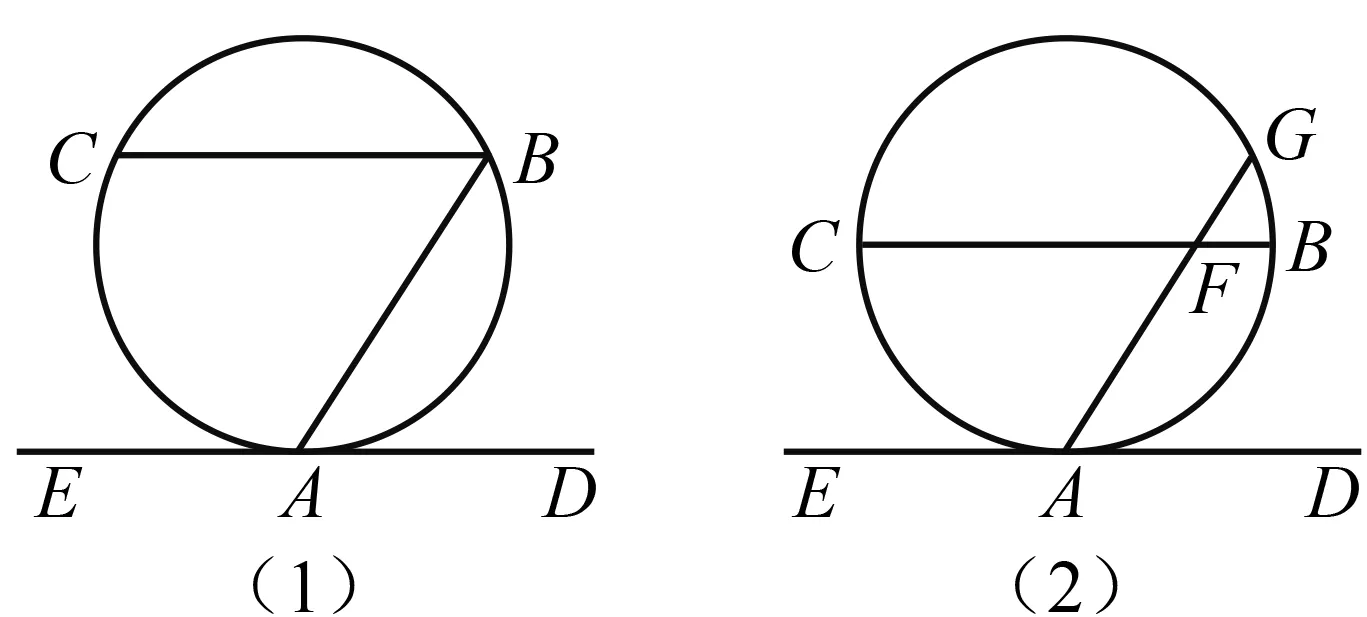

7.3 垂径定理法

7.4 动态法


8 教学启示

