有结构地学习三位数乘两位数笔算

文|许含英

三位数乘两位数是在两位数乘两位数、三位数乘一位数的基础上学习的，如何有结构地学习三位数乘两位数笔算？可以安排以下教学活动。

一、复习：唤起已有经验

有A、B 两款篮球，价格分别是45元、145 元。如果买12 个A 款篮球，一共要多少钱？

独立列式计算。反馈时，结合情境，复习竖式每一步表示的含义。引导回顾竖式计算的方法：把45×12 拆分成45×2和45×10 分别计算积，再把这两个积相加，也就是两步乘和一步加，先分后合。

二、探索：促进代数推理

如果买12 个B 款篮球，一共要多少钱？145×12。算一算，写出计算过程；想一想，每一步表示的含义。

学生独立练习后，全班交流。

方法一：145×12=145×2×6=290×6=1740。

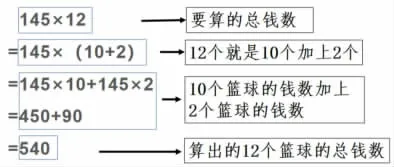
方法二：145×12=145×（10+2）=145×10+145×2=1450+290=1740。

借助情境理解每一步的含义。12 个篮球的总钱数是145×12。12 个篮球的总钱数是10 个篮球的钱数（145×10）加上2 个篮球的钱数（145×2）。

方法三：列竖式计算。

学生说竖式计算的过程。师生交流讨论，明确竖式计算方法：

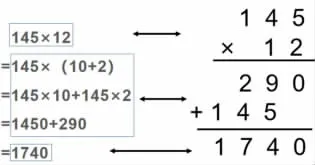
先用个位上的2 乘145，表示2 个一乘145，得到290 个一，290 是2 个篮球的价钱；再用十位上的1 乘145，表示1 个十乘145，得到145 个十，145 代表1450，0 可以省略不写，5 与十位对齐，1450 是10 个篮球的价钱。再把290 和1450 相加得到1740，也就是12 个篮球的价钱。

把横式与竖式的计算过程对应。

三、比较：沟通方法联系

出示横式和竖式，有什么相同和不同？

师生讨论得出：第一个乘数不同。计算方法相同，都是先用两位数个位上的数去乘，得到几个一，再用两位数十位上的数去乘，得到几个十，最后把两次乘得的积加起来，都是先分后合，结构相同。

四、练习：巩固算理算法

排球105元，手球198元，足球290元。

1. 李教练买了15 个球，大约用了3000 元。他买的可能是（ ）球。

2. 如果要买34 个排球，需要多少钱？

3.如果要买24 个足球，需要多少钱？

以上教学，学生经历“观察、思考、推理、比较”的学习过程，有结构地探索三位数乘两位数的笔算方法，有效进行算理和算法的迁移，发展运算能力和推理意识。