基于传统拼合方式的胶合木柱轴压试验研究

程小武,余泓睿,史明炎,孙小鸾,陆伟东

(南京工业大学 土木工程学院,江苏 南京 211800)

无论是在古代还是现代,大截面的木构件一直是很难获得的。为了解决这个难题,北宋年间成书的《营造法式》卷三十中就已经提出了由小材拼合成大材的方法。梁思成[1-2]率先对《营造法式》进行了研究,并留下了诸多著作供后人参考。

根据榫卯节点连接方式可以分为公母榫、直榫、燕尾榫、管脚榫、馒头榫和搭扣榫6大类[3],并且同种榫卯结构在不同方向荷载下具有不同的力学性能[4]。透榫和燕尾榫节点在改变摩擦因数的情况下,破坏模式、延性、承载力均没有发生明显变化[5],对于燕尾榫来说,榫高、榫长和摩擦因数对其初始转动刚度和极限弯矩承载力的影响最大[6]。在不同角度下的燕尾榫连接中,其中连接抗拉强度最大的是正交连接[7],并且燕尾榫的拉压、剪切破坏一般发生在榫头与卯口[8]。

关于木柱的轴压性能研究基本上是以试验为基础,有限元模拟进行验证,最后理论值与试验值对比,其中包括内置H型钢外包胶合木的组合柱[9]、压缩木销连接拼合柱[10]、由规格材(SPF)组成的空心木柱[11]、落叶松胶合木短柱和长柱[12]的轴压试验。

霍亮亮等[13]得到了由铁杉规格材加工成的交叉层合木柱(CLT)构件的轴压稳定系数公式。Wei等[14]主要研究了CLT和层板胶合木柱(GLT)的轴压特性。Malhotra等[15]对以可靠性为基础的拼合柱极限状态设计公式发展进行了描述。Kimble等[16]通过提出影响因子(Cs)来修改规格材中弹性模量的下限。Bryant等[17]得出影响组合柱极限承载力的主要因素是单根木材的性能、整体几何尺寸、节点刚度、试验加载方式。王龙等[18]通过对传统木结构柱脚模型施加集中力来模拟竖向荷载,最后对比了试验和有限元模型的滞回曲线。谢启芳等[19]利用ABAQUS软件对4种受损程度的木柱进行了有限元分析。文献[20-21]运用有限元模拟了振动台试验,并得到了大量的数据用来分析其加固效果。Lartigau等[22]基于胶合木植筋节点的试验破坏模式和有限元应力云图，提出了新的节点设计方法。

祝恩淳等[23-24]在基于各国木结构设计规范中稳定系数的计算方法上,提出了新的适用于各类木产品构件的稳定系数统一公式以及钢板螺栓连接承载力计算式。Li等[25]拟合了竹制复合材料柱的稳定系数-长细比曲线,并提出了相应计算式。Theiler等[26]针对木柱的轴压和偏压承载力提出了一种基于应变的计算方法。Jumaat[27]以矩阵级数法对组合柱进行了计算。

目前,国内外对木柱的研究多是以利用化学结构胶拼合原理一次制成的现代胶合木为主,其中对拼合柱的研究也是以原木拼合成的圆柱为主,对胶合木柱拼合的研究较少。为研究传统木结构拼合方法在现代木结构建筑中的应用,本文进行了一系列的试验来研究燕尾榫连接的拼合柱的轴压性能,将长细比、暗鼓卯榫高作为试验变量,结合试验结果综合分析了各参数对拼合柱轴压性能的影响。

1 试验

1.1 试件材料

拼合柱的柱体采用北美花旗松,榫卯连接件采用澳洲桉木,均符合《胶合木结构技术规范》[28]的设计要求,其中,北美花旗松、澳洲桉木的密度和平均含水率分别为0.52、0.71 g/cm3和12.4%、14.0%,具体物理力学性能见表1。

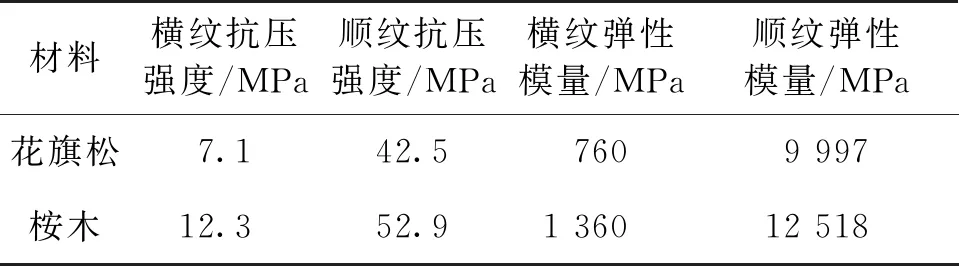
表1 花旗松和桉木物理力学性能

1.2 试件设计

为了研究长细比(λ)和暗鼓卯榫高(h0)对拼合柱极限承载力的影响,本试验共设计了7组,并加上1组相同截面尺寸的GLT组作为对比,以《营造法式》中合柱鼓卯两段合为参考,确定相应构件的尺寸,所有试件截面尺寸均为240 mm×240 mm,具体分组及尺寸见表2。

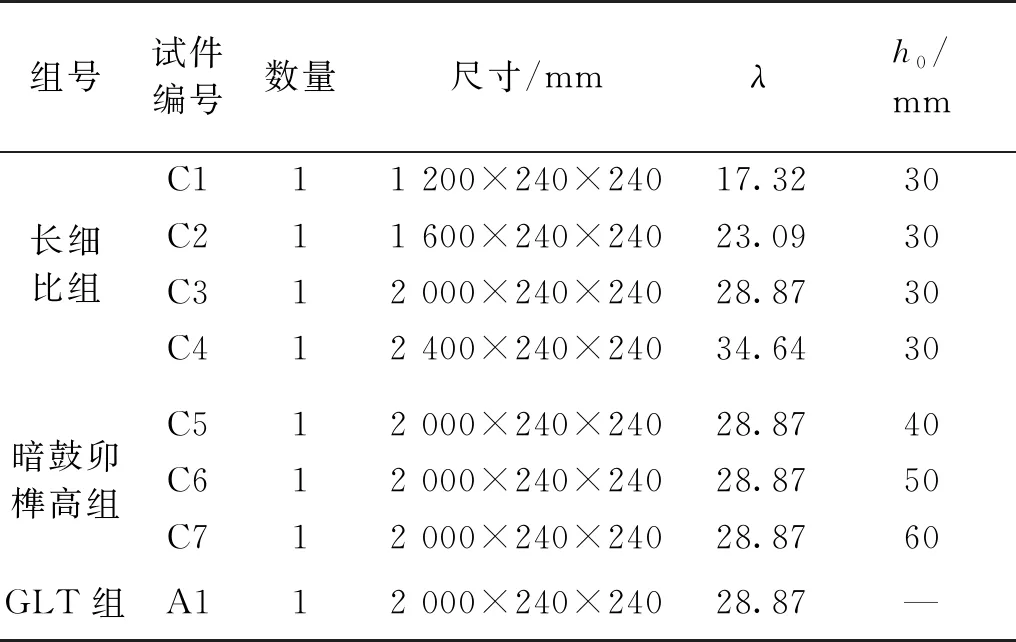
表2 轴压试件参数

《营造法式》中合柱鼓卯图样中有二段合、三段合、四段合,即对应由2、3或4根圆木拼成一个完整的柱身。鼓卯有明有暗,明鼓卯用在柱面或柱底；暗鼓卯用在柱心,鼓卯底广面狭,另一段作榫则面广底狭,从而榫卯相合。

明鼓卯、暗鼓卯、儹楔样式见图1,具体尺寸和数目见表3,表3中数目为试验中所有拼合柱所需鼓卯和儹楔的数量。

图1 鼓卯和儹楔示例

表3 燕尾榫和儹楔尺寸和数目

在上述试件全部加工完成后,依次按照安装暗鼓卯、安装儹楔、合柱、安装明鼓卯的顺序完成木柱的拼合,具体拼合顺序如图2所示。

图2 拼合顺序

1.3 试验设备与加载方法

轴心受压试验使用的加载装置是量程为20 MN的电液伺服作动器。试件顶端通过加载板连接球铰,底端抵靠于反力基座,因此整个加载过程可看作一端铰接、一端固支。试验加载装置示意图如图3所示。

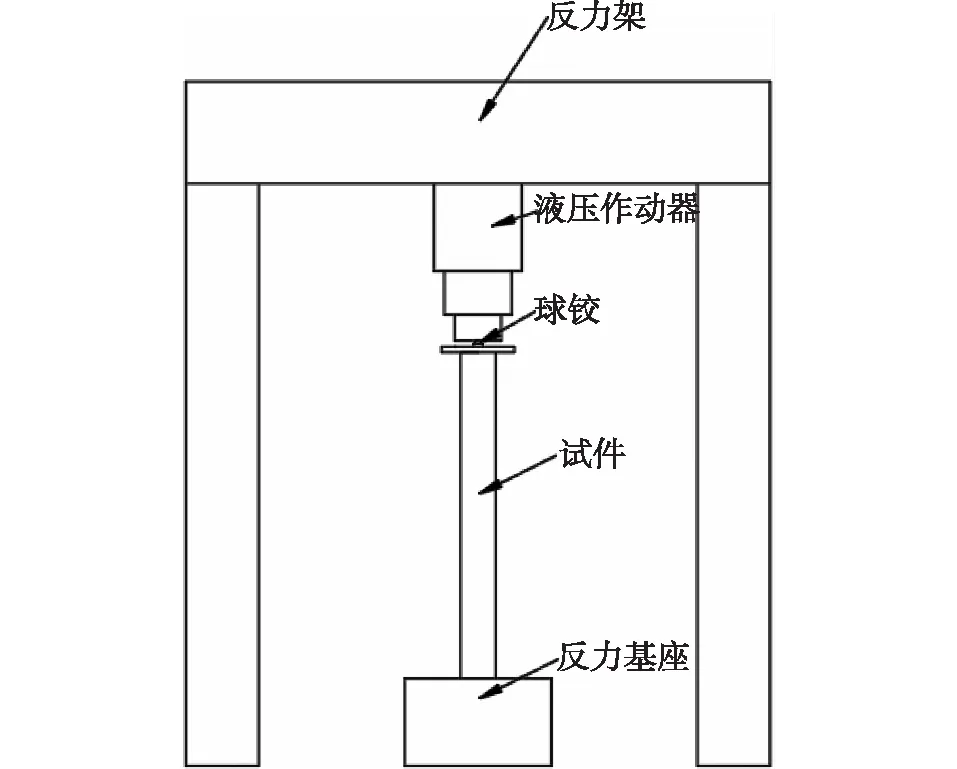
图3 试验设备示意图

本试验使用BX120-50AA型应变片测量拼合柱和GLT的应变,在拼合柱的每个侧面柱中、距离两端200 mm处各贴1个纵向应变片,在拼合柱非拼合面柱中粘贴1个横向应变片,共计14个。使用量程为100 mm的拉杆式位移计测量试件的水平位移,选择试件的一组相邻面,分别在其柱中、距离两端200 mm处各放置1个位移计,共计6个。应变片和位移计的布置如图4所示。

L为试件高度

在正式加载前,对拼合柱进行了几何对中和物理对中,几何对中是保证球铰加载板、试件几何中心、反力基座三者中线在同一条竖线上;物理对中参考《木结构试验方法标准》[29]，即先对试件预加载,然后再正式加载。应变箱采集仪以5 s/次的频率采集相对应的应变和位移,正式加载采用位移加载,加载速度为1 mm/min,匀速加载至试件破坏。

2 试验结果

2.1 破坏模式

在加载初期,试件表面无明显破坏现象。随着荷载的逐渐增大,试件表面的褶皱和纵向裂缝越来越多,试件内部发出的纤维挤压声越来越大;当荷载降低至峰值荷载的80%左右时终止试验,最后得到拼合柱两种典型的破坏模式:横向裂缝和纵向裂缝破坏,结果如图5所示。

图5 拼合柱的典型破坏模式

这两种破坏模式出现在包括A1组在内的全部试件的轴压试验现象中,属于木柱轴压典型的破坏模式,由此可知:拼合柱和GLT的破坏模式主要是强度破坏。本次轴压试验结果的汇总见表4。

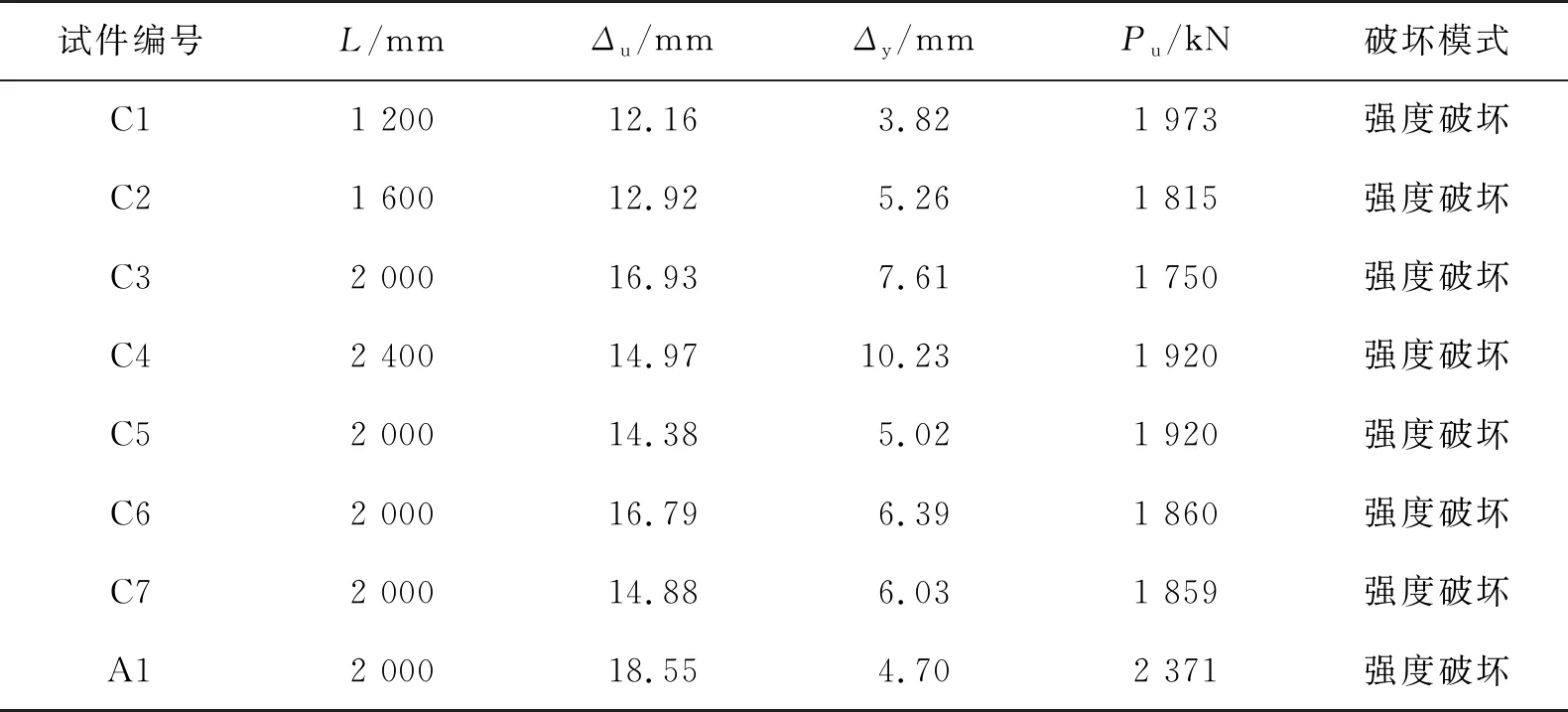
表4 轴压试验结果统计表

2.2 荷载-位移曲线

为了便于直观比较,将荷载-轴向位移曲线、荷载-柱中侧向位移曲线分为长细比组、暗鼓卯榫高组,其中GLT组绘制于暗鼓卯榫高组中。

荷载-轴向位移曲线如图6所示。由图6可知:各试件都经历了弹性、弹塑性、塑性3个工作阶段;拼合柱的极限承载力可达到GLT组的73.81%～80.98%。图7和8分别为长细比组和暗鼓卯榫高组的荷载-柱中侧向位移曲线,其中拼合柱有拼合面和非拼合面两种侧面。由图7和8可知:在加载前、中期,试件均没有出现明显的侧向变形；当荷载加载到极限承载力的85%左右时,试件侧向位移骤然增大,且随着荷载的增大而逐渐增大;试件的非拼合面位移与相应的拼合面位移相比,高出60%左右，并且随着长细比的增大,试件的侧向位移也随之增大。

图6 荷载-轴向位移曲线

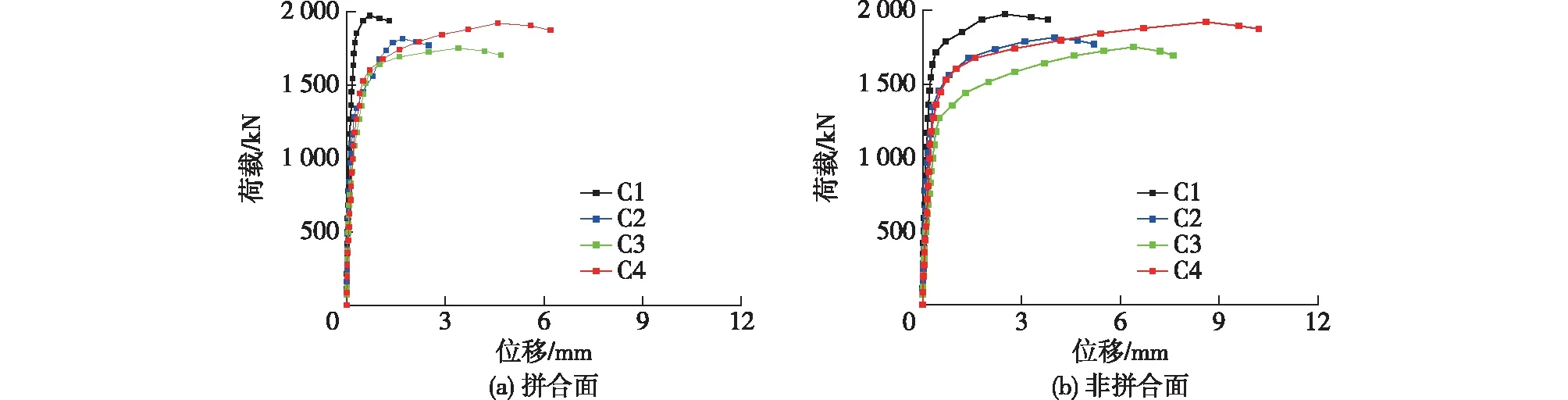
图7 长细比组荷载-柱中侧向位移曲线

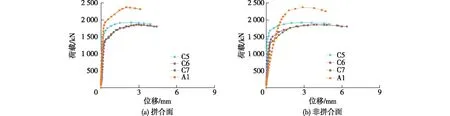
图8 暗鼓卯榫高组荷载-柱中侧向位移曲线

2.3 荷载-应变曲线

假定拉、压应变分别为正和负值,则各试件的荷载-应变曲线如图9所示。

由图9可知:拼合柱轴心受压的应变最大值随着长细比的増大,呈现先不变后逐渐减小的趋势；暗鼓卯榫高对试件的荷载-应变曲线影响不显著。

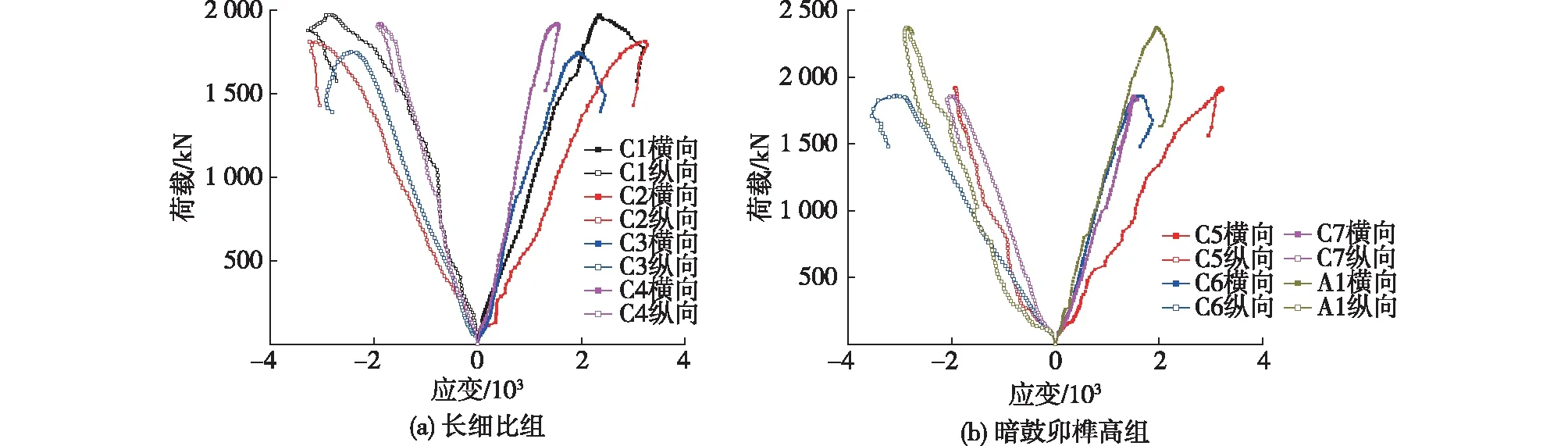
图9 荷载-应变曲线

3 有限元模拟结果

由于多个部件之间存在的接触较多,在模拟分析时会发生变形,因此本文选用八节点六面体线性减缩积分(C3D8R)实体单元,该单元适用于变形且不易自锁的部件模拟。在全部试件的模拟分析中,胶合木柱体选择边长为20 mm的单元网格进行划分,燕尾榫、儹楔选择边长为5 mm的单元网格进行划分。

为了更接近试验结果,位移加载速度设置为1 mm/min;试件底端边界条件设置为完全固定,顶端边界条件设置为轴向位移有自由度;将模型顶面耦合于上方一点,并对其施加边界条件,使其进行位移加载。

接触主要包括暗鼓卯榫连接两段柱体的接触、两段柱体之间的接触、明鼓卯连接两段柱体的接触,其中法向面面接触设置为“硬接触”,切向面面接触设置为“各向同性”,摩擦因数设置为0.45。

3.1 应力及位移云图

使用ABAQUS软件模拟试验,得到了各组试件的应力及位移云图。图10为试件C3的应力和位移云图。由图10可知:各组试件的应力云图大致相同,整个模型除了明鼓卯附近和少部分位置,绝大部分柱体已经达到了屈服荷载,最大应力主要存在柱底部的明鼓卯中部头榫处。由于木材本身各向异性,各组试件的位移云图各不相同。

图10 整体变形云图(C3试件)

3.2 试验和模拟结果对比

图11和12分别为长细比组和暗鼓卯榫高组的荷载-位移曲线。将8组轴心受压试验数据与有限元模拟结果汇总于表5中。由表5可以得出:轴向位移、柱中侧向位移、极限承载力的误差平均值分别约为10.27%、7.49%和5.84%。

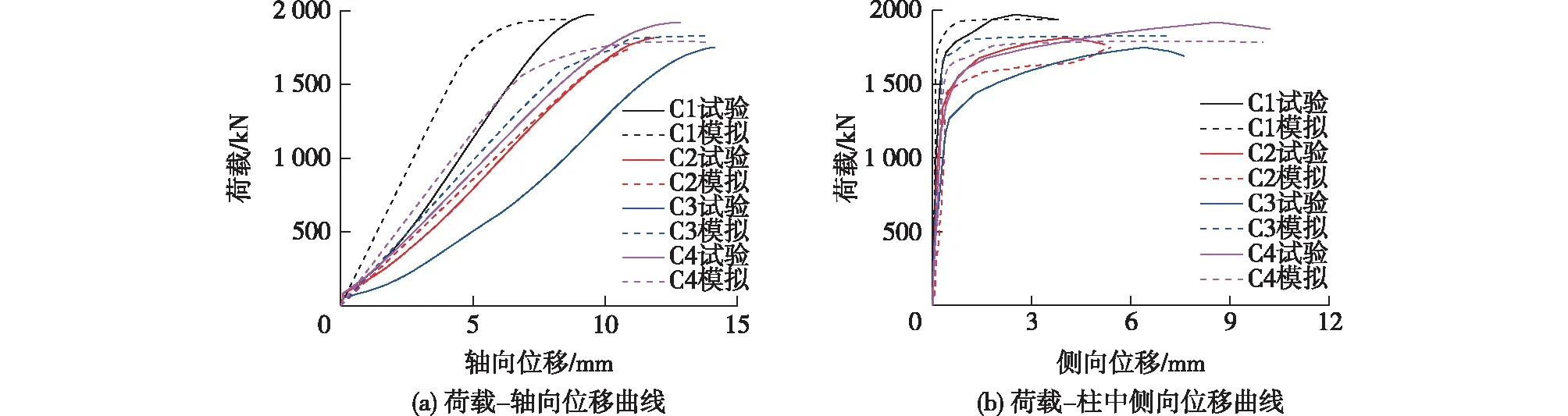
图11 长细比组荷载-位移对比曲线

4 极限承载力计算

拼合柱的极限承载力理论值是根据《木结构设计标准》[30]《美国木结构房屋国家设计标准》[31]《欧洲木结构设计标准》[32]《加拿大木材工程设计标准》[33]计算所得,并与模拟值进行对比,以研究现有规范对拼合柱的适用性和准确性。

4.1 极限承载力试验值与理论值对比

极限承载力有限元模拟和试验结果的误差基本在10%以内(表5),因此，可将有限元模拟结果代替试验值与计算值进行对比,具体结果如表6和图13所示。

表5 模拟与试验结果对比

由表6和图13可以看出:有限元模拟结果和4种木结构规范标准计算值曲线的趋势大致相同,但各国木结构规范标准计算结果均大于有限元模拟结果，这是由于各国理论计算值是以GLT的设计参数计算得到的,并且没有提及使用燕尾榫连接时的调整系数(φc),因此φc的推出是有必要的。

图13 模拟结果与各国规范对比

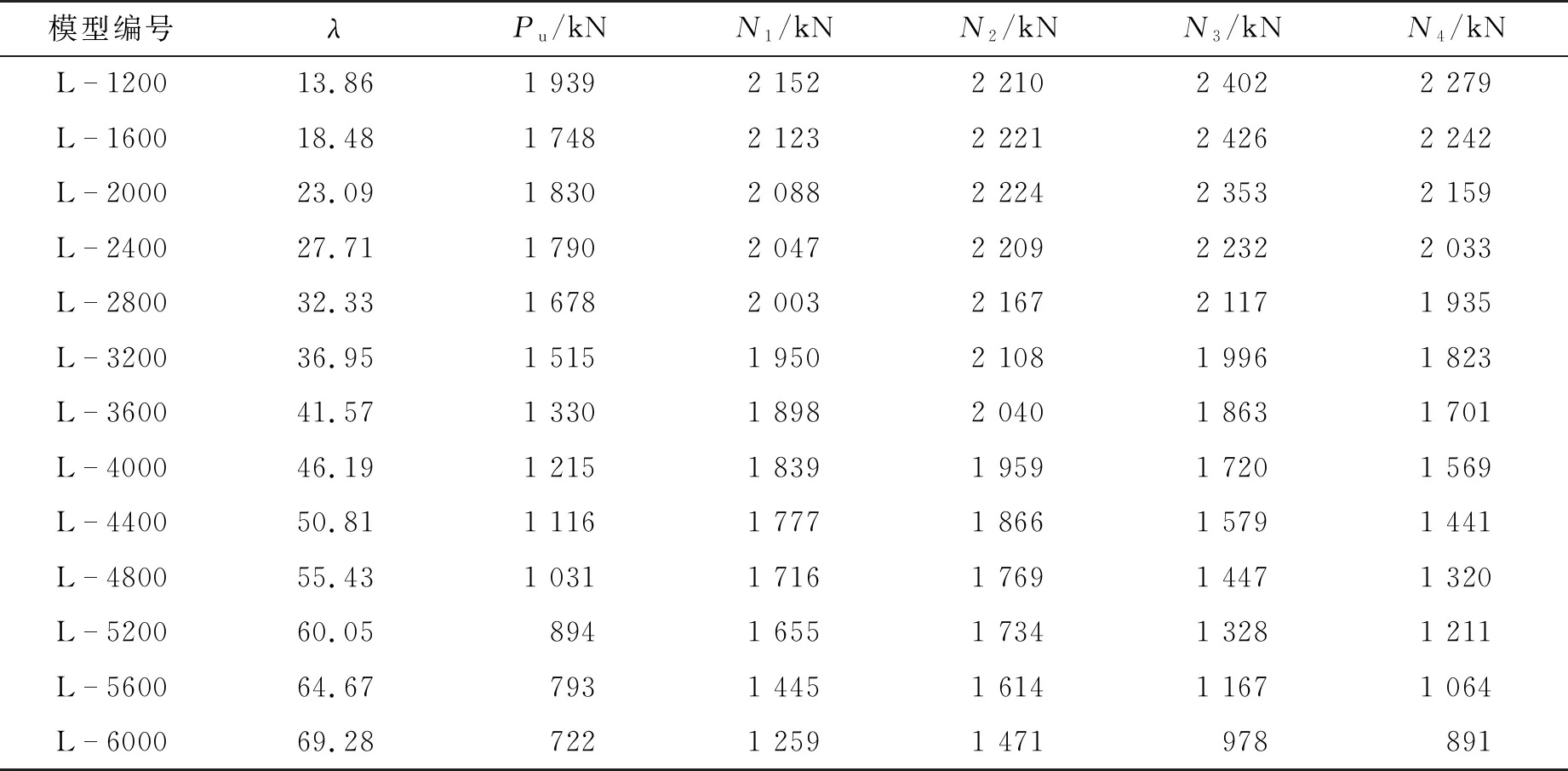
表6 拼合柱极限承载力计算结果

4.2 调整系数计算式

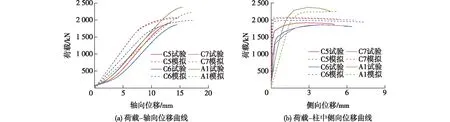
图12 暗鼓卯榫高组荷载-位移对比曲线

由表7和图14可以看出:经过调整后的各国理论值与有限元模拟值更为吻合。调整后的欧洲和加拿大理论值更加接近有限元模拟值,而调整后的中国和美国理论值在长细比较小时比较保守,长细比较大时偏大。

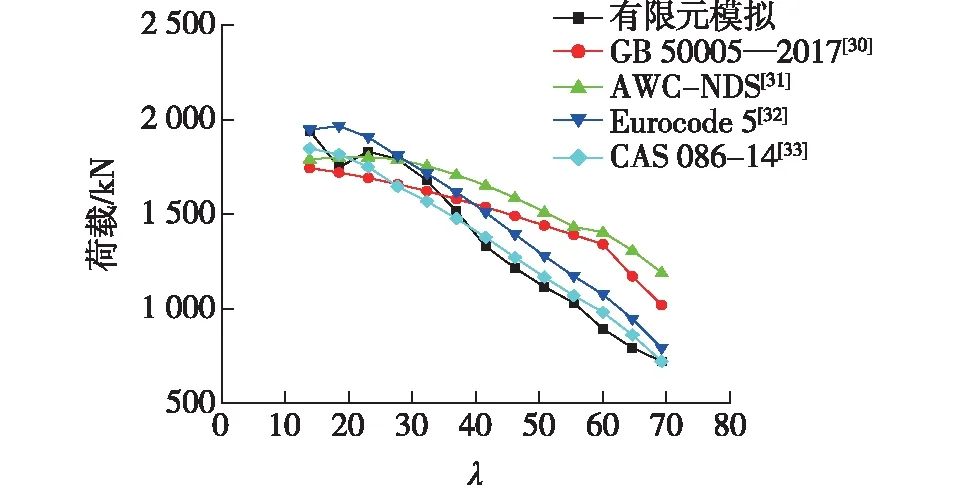
图14 模拟结果与调整后的各国规范计算结果对比

图15为由模拟结果得出的调整系数与长细比的关系。由图15可知:随着长细比的增大,调整系数逐渐减小,由此拟合得出调整系数与长细比的经验公式,如式(1)所示。

(1)

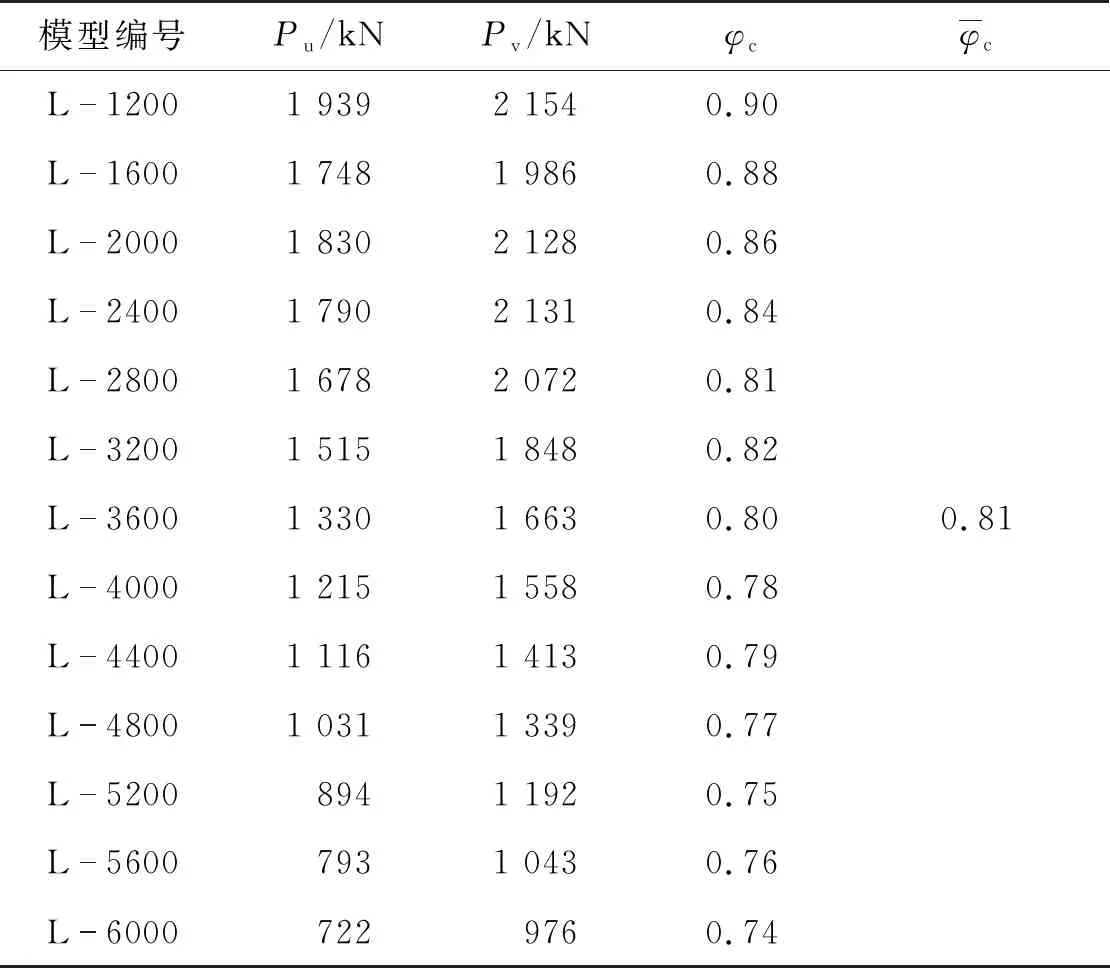
表7 调整系数计算结果

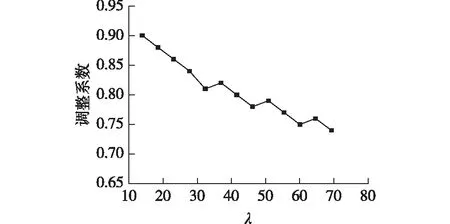
图15 调整系数-长细比曲线

综上所述,拼合柱的极限承载力计算值可由木结构规范标准理论值与调整系数相乘得到,拼合柱的极限承载力计算式如式(2)所示。

Nc=N1φc

(2)

式中:Nc为木结构设计标准理论值。

5 结论

通过对拼合柱进行轴压试验、有限元模拟、理论验证、推出调整系数等,研究拼合柱的轴压力学性能,主要结论如下:

1)拼合柱和GLT的主要破坏模式均为强度破坏,拼合柱的极限承载力可达到GLT的73.81% ～ 80.98%,随着长细比的增大,拼合柱的轴向位移和侧向挠度也随之增大,峰值荷载和峰值竖向应变随之减小,暗鼓卯榫高对拼合柱的影响不显著。

2)有限元模拟曲线和试验曲线大致吻合,并且轴向位移误差约为10.27%,柱中侧向位移误差约为7.49%,极限承载力误差约为5.84%,说明有限元模拟结果较为可靠。

3)现有拼合柱计算方法均无法准确预测使用燕尾榫连接的拼合柱的极限承载力,取拼合柱极限承载力模拟值与GLT极限承载力模拟值的比作为调整系数,并将模拟结果与调整后的各国规范计算值对比,绘制出调整系数-长细比曲线,可总结出φc的计算式。