爆炸载荷作用下网壳结构动态响应研究进展

朱精忠,周丰峻,李九一,周金仁,赵 辉

(1.中国人民解放军军事科学院 国防工程研究院,北京 100850;2.江苏省响水县公安局,江苏 盐城 224600;3.中国人民解放军32378部队,北京 100850)

网壳结构是一种在国内外颇受关注并有广阔发展前景的空间结构,大量用在体育场馆、歌剧院、火车站、机场航站楼以及地面雷达天线罩等各种民用或军用工程领域(图1和2)。网壳结构是将杆件沿着某个曲面有规律地布置而组成的空间体系,其受力特点与薄壳结构类似,是以“薄膜”作用为主要受力特征的,即大部分载荷由网壳杆件的轴向力承受[1]。随着大跨度网壳结构的出现及其在大型公共建筑中的广泛应用,如何解决网壳结构在阵风和地震等随时间变化的载荷作用下的非线性动力学行为问题变得迫在眉睫,因而也越来越受到研究者的关注。除阵风和地震载荷外,爆炸载荷也是网壳结构的一个威胁来源,和平时期,由于人员聚集在民用的大跨度网壳建筑结构中,因而容易成为暴恐袭击的首选目标;战争时期,针对雷达天线罩等大跨度网壳结构设备的打击能决定战场的胜负。因此,对此类大跨度网壳结构进行抗爆防护研究具有重要的理论和现实意义。

图1 国家大剧院

图2 地面雷达天线罩

爆炸载荷下,常用的网壳结构动态响应的研究手段有:试验检测、理论分析和数值模拟。研究对象无论是足尺结构、缩尺模型结构还是一般结构构件,试验检测往往都能够为研究人员提供丰富且有用的试验数据,但是试验测试耗材昂贵、试验成本高,且在工程实际应用中,多数情况下受环境条件制约,很难开展试验检测。理论分析通常是基于弹性板理论、Timoshenko梁模型和单自由度模型等理想化模型建立的,这些理论可以为研究人员提供结构构件的损伤定位,帮助其制定相应的损伤判据,但理论分析往往不能真实地反映实际情况下复杂的爆炸载荷和结构条件。而数值模拟方法可以缩短设计时间和降低设计成本,在试验检测无法完成的情况下,可以通过数值模拟对各个区域和测点进行应力和位移分析,但在模拟分析过程中,往往要对边界条件和材料属性进行简化,且计算量和计算精度受设备限制。近些年来,随着计算机的高速发展,使用数值计算方法来预测网壳结构的动力响应越来越普遍。本文对已有的网壳结构稳定性分析和爆炸载荷理论进行了回顾,综述了网壳结构在动载荷作用下采用数值方法研究响应的发展、特点和应用。

1 网壳结构稳定性分析的理论研究进展

随着工程技术的发展,网壳结构的设计在不断优化,在追求大跨度的同时,力求厚度薄和质量轻。与此同时,网壳结构稳定性计算和验证已成为重点研究的问题。近几十年,国内外学者对在动力载荷作用下的网壳稳定性问题开展了大量研究[2-5],使网壳结构的动力稳定性理论得到长足发展,并取得丰硕的成果。

在20世纪70年代之前,由于数值计算方法和计算机计算能力的局限性,无法对具有成千上万个自由度的网壳结构进行有效数值模拟,一般都是借助于连续化理论将网壳转化为连续壳体结构(拟壳法),通过特定的解析方法,从而求出壳体结构的稳定承载力,但连续壳体的稳定性理论本身并未完善,仅对少数壳体(如球面壳)才可以获得实用的公式。为了求得球面壳体稳定性承载力,von Karman等[6]首次指出,薄壳结构不稳定屈曲后的性能是导致该类结构线性理论和试验结果之间存在巨大差异的决定因素。在此后对网壳结构稳定性的研究中,研究者们受此启发进行了大量的理论探索,并且在俄罗斯著名数学家Lyapunov提出的经典运动稳定性理论的基础上,研究者们提出了网壳结构动力不稳定性判别准则[7-8]，应用该准则,使得结构刚度矩阵行列式的取值问题得到了解决,因而网壳的稳定性能够很容易地通过刚度矩阵的正定或负定来判断。通过这些标准,将更有利于人们理解网壳结构动力不稳定问题的基本概念；但是,由于网壳结构过于复杂,在实际工程问题中,该准则很难得到一个定量的结果。因此,Shen[9]和郭海山等[10]系统分析了网壳结构动力稳定性的研究方法,提出了动力响应全过程曲线的概念,并结合结构的时程响应曲线,提出了网壳结构在地震等复杂载荷作用下的动力稳定性实用判别方法。

Kassimali等[11]通过分析关节位移为任意值的欧拉公式,考虑了3种随时间变化的力函数,即无限长的阶跃载荷、有限长的三角形载荷和正弦载荷,对空间铰接杆系结构的几何非线性动力稳定性进行了分析,给出了结构在这些载荷下的变形曲线。Kim等[12]考虑有阻尼作用存在时,针对阶跃载荷作用下壳体结构的动力失稳问题进行了研究。Karagiozova等[13]对在轴向冲击载荷下圆柱壳的屈曲特性进行了系统化的研究,通过理论分析、试验研究和数值模拟相结合的手段得到了失效模式与冲击速度及被冲击物动态力学性能之间的关系。Gioncu[14]综述了解决网状壳体屈曲问题的最新技术。Han等[15]对焊接空心球面节点的刚度特性及其对单层球面网壳稳定性能的影响进行了探讨,给出了焊接空心球节点初始刚度的理论和实用公式,并分别得到了弹性和弹塑性临界位移和转角。Yu等[16]研究了在强震作用下,网壳穹顶子结构对破坏行为的影响。Zhi等[17]综合考虑全过程分析和材料损伤积累,系统地研究了单层网壳在突加载荷、简谐作用和地震作用下的动力性能和破坏模式;同时,为了分析不同的失效机制,提出了基于模糊综合评判理论的失效模式识别技术,并通过实例验证了该方法的可行性。Fan等[18]在考虑构件的初始曲率带来的几何缺陷后,对单层网状穹顶弹塑性稳定性进行了研究。对于按我国规范设计的球面网壳,Cui等[19]利用同步自回归模型(SAR)评估了其整体失稳承载力概率分布和可靠度,结果表明：整体失稳的临界载荷系数对初始几何缺陷的假定形状和分布模型敏感。Orlando等[20]研究了浅层双稳态规则金字塔桁架的静力和动力屈曲,给出了考虑大位移、大转动、小应变的金字塔浅桁架非线性静力和动力分析的精确公式。

沈世钊[21]对2 800余例实际尺寸网壳结构进行了载荷-位移全过程分析,从理论上总结了网壳结构稳定性的变化规律,并且提出了网壳结构稳定性验算的实用公式。范峰等[22]综述了国内外半刚性节点及半刚性节点单层网壳结构已有的研究成果,并指出对半刚性节点网壳结构的动力稳定性等方面有必要进行更多、更深入试验和理论研究,以推动半刚性节点单层网壳结构的实际工程应用。石瑛莉[23]基于拆除构件法对湖南长沙高铁新城吾悦广场的屋面采光顶网壳结构抗连续倒塌进行了分析和研究。李海旺等[24]通过冲击试验的方法,用落锤单层撞击 Kiewitt-8(K8) 型网壳模型,研究了在撞击作用下 K8 型单层网壳的动力稳定性,这是国内外大跨空间结构领域较早的关于结构抗冲击的研究。王多智[25]对Kiewitt-6(K6) 型单层球面网壳进行了缩尺模型试验,并将试验结果与数值结果进行比较,验证了其建立的网壳结构冲击响应方法的正确性。林莉[26]研究了在网壳结构中经常使用的钢动态本构模型和失效模型,得出了网壳结构在冲击动力下的响应特点及失效规律。苏倩倩等[27]以拉格朗日方程为基础,提出了一种适用于简支梁和K8型单层球面网壳，在三角形爆炸载荷作用下动力响应的计算方法。胡晨晞[28]综合考虑几何和材料非线性、冲击接触以及边界条件等因素,对单层网壳结构在物块碰撞作用下的冲击响应,提出了计算网壳结构最终位移响应的拟壳法和直接计算方法。朱钊辰等[29]采用基于等效Marshall模型的精细化构件模型，进行了结构动力响应分析,并对一个缩尺K6型网壳模型进行振动台试验和有限元模拟,结果表明：基于等效 Marshall 模型的精细化构件单元可以准确模拟构件受力状态的动态变化过程,既能精确模拟构件的实际受力状态,又能最大程度提高计算效率。

从目前的研究来看,有关网壳结构在爆炸载荷作用下的理论研究偏少,且目前大多数的研究都是针对规则的网壳结构(如K6、 K8型网壳结构),但是对于一些具有特殊用途的新型空间网壳结构在爆炸载荷作用下的动力响应的研究尚未形成体系[30]。

2 爆炸载荷研究概况

空中冲击波的载荷属性取决于许多因素,包括炸药的质量和形状、爆炸时炸药与被炸物体之间的距离以及网壳结构的几何和材料特性等。本节简要概述爆炸载荷的传播、计算及数值分析手段的研究进展。

2.1 爆炸载荷的传播

爆炸是指物质状态突然的发生物理或化学变化,并伴有运动和能量释放[31]。爆炸问题可分为内部问题、外部问题、组合问题和边界问题。内部问题研究在释放能量的物质中所发生的过程;外部问题讨论在药包周围介质中所发生的过程;组合问题研究的是和外部问题相同的过程,但过程是发生在释放能量的介质中;边界问题讨论爆炸波和物体之间的相互作用[31]。网壳结构在爆炸载荷下的动态响应属于边界问题。

炸药一旦被引爆,就会产生一个高度压缩的局部区域,并迅速膨胀。爆炸反应开始后,爆轰波以6～8 km/s的速度通过未反应的爆炸材料,固体爆炸材料被有效地转化为热的高压气体,其瞬时最高温度约为3 000 ℃,峰值压力高达40 GPa。由于高压的作用,气态爆轰产物迅速膨胀到原来装药体积的4 000倍左右[32]，气体的快速膨胀几乎瞬间将周围的空气压缩成冲击波。冲击波在传播过程中的空间压力分布如图3所示。冲击波是一种高压压缩波,它以比声速更快的速度在空气、水或其他介质中传播。冲击波在空气中传播的一个显著特征是,冲击波阵面会在所有气体动力条件下引起几乎瞬间的阶跃变化,包括静态压力、密度、流速和温度[32]。

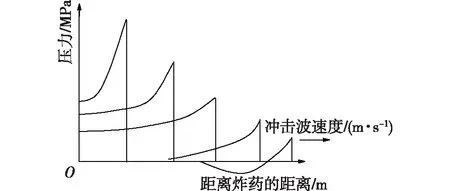
图3 爆炸冲击波的传播[32]

在空气中,炸药爆炸后,冲击波产生的压力瞬时上升,然后迅速衰减,其超压-时间曲线如图4所示。由图4可知：该曲线显示正超压随时间呈指数衰减,这可以使用修改的Friedlander表达式[33]来计算,如式(1)所示。

图4 理想空气中的爆炸超压时程曲线

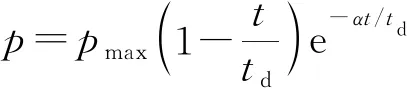
(1)

式中:p为瞬时超压;pmax为t=0时的峰值超压,即冲击波刚开始到达时的激波阵面压力;td为正压相持续时间;α为比例系数。

与理想爆源产生的冲击波不同,非理想爆源产生的冲击波具有作用面积大、时间长、超压低、冲量大的特点[34-35],冲击波效应与爆炸源的性质密切相关。

2.2 爆炸载荷的计算

在实际应用中,常用三硝基甲苯(TNT)当量来描述炸药的质量,可以通过量纲分析和爆炸比例定律,得到比例距离(Z)[37],这是一个带有量纲的空间距离参数,如式(2)或(3)所示。

(2)

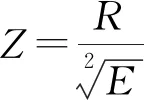
(3)

式中:R为被炸物体距爆炸源中心的距离,W为炸药质量,E为炸药能量。

在任何关于爆炸波形成的物理研究中,都说明爆炸源的重要参数为总能量和能量密度,即单位体积或单位质量的能量,因此,在理论研究中,使用E进行计算要比使用W好。在工程应用中,炸药质量更易获得,所以一般使用W。

在空气爆炸中,pmax是主要的研究对象，可以通过试验发现以及结合理论分析,从而得到经验公式。一些学者总结了pmax的经验公式,其中应用比较广泛的是Henrych公式,如式(4)所示。

(4)

我国《国防工程设计规范(草案)》中,也提出了相应的计算公式,如式(5)所示。

(5)

此外,也有学者是通过试验研究爆炸波在不同介质中的传播规律,从而总结出在不同介质中爆炸波的主要基本参数随传播距离变化的规律[38-40]。

当炸药在空中爆炸时,在爆心正下方冲击波的传播方向与地表垂直,冲击波阵面后的空气质点也以很高的速度随着波阵面运动,向着目标(地面)传播的冲击波被称为入射冲击波[41]。当入射冲击波与固壁平面相遇后,固壁平面附近的空气压力提高,这种状态将逐渐反向向上传播,形成反射冲击波；冲击波垂直于固壁平面入射时,发生的反射为正反射,反射冲击波经过后的区域由于经历了两次冲击波的作用,该区域压力明显增大,对于在空气中传播的强冲击波,反射压力通常为入射压力的8倍，甚至更大；当冲击波阵面与固壁平面成一定角度入射时,则发生斜反射。随着离爆心投影点距离的不断增大,入射角度越来越大,当反射波阵面赶上，并与入射波阵面贴合,成为一个合成波时,这种反射现象成为马赫反射,该合成波被称作马赫波。对于正反射,可以通过理想气体状态方程联立求解,得到空中反射冲击波超压计算公式,如式(6)所示。

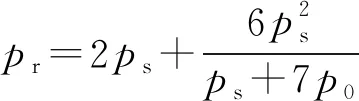
(6)

式中:pr为冲击波的反射超压,ps为入射超压,p0为空气中未发生扰动时的大气压力。

对于规则反射,可采用经验公式计算反射超压,如式(7)所示。

(7)

式中:φ为入射角。

2.3 爆炸载荷的数值分析手段

除了通过试验总结经验公式外,还可以通过流固耦合算法(FSI),在计算机软件中模拟爆炸波与引起结构内部运动或变形的目标结构的相互作用,流固耦合算法在理论、计算和试验上都得到了广泛研究。计算分析爆破载荷效应的常用软件有 ABAQUS 、 ANSYS/LS-DYNA和AUTODYNA等。

Chafi等[42]提出了一种能够预测爆炸波与结构相互作用问题相关方面的计算方法,包括爆炸波在介质中的传播和结构在爆炸载荷作用下的响应,提出了如何通过任意拉格朗日-欧拉多材料公式的移动网格,将流体作为移动介质来模拟流固耦合；如何使用拉格朗日公式在可变形网格上处理该结构。Teich等[43-44]推导了一个新的耦合模型,该模型考虑了流固耦合算法和周围空气产生的气动阻尼,是在与质量和结构刚度相关的等效黏滞阻尼比的基础上建立的。卢红琴等[45]采用ANSYS/LS-DYNA 有限元软件,对中国人民解放军后勤工程学院的坑道试验模型进行数值模拟,通过比较数值模拟和试验值,发现二者结果比较吻合,说明了数值模拟方法的可行性。张如林等[46]基于ANSYS/LS-DYNA 软件、Arbitrary Lagrange-Euler(ALE)算法和流固耦合理论建立了爆炸冲击波的数值分析方法,通过对数值结果与试验数据、经验公式计算结果的比较分析,确认了数值技术的有效性。高轩能等[47]应用ANSYS/LS-DYNA有限元软件建立了模拟TNT爆炸的数值计算模型,并进行了空爆冲击波超压等数值计算,通过数值计算、经验公式和试验结果的对比分析,验证了计算模型和参数取值的可信性。Cui等[48]结合有限差分法(FDM)和物质点法(MPM)的优点,提出了一种耦合有限差分物质点方法(CFDMP),在激波管问题和二维氦气爆炸模拟中，验证了该算法的准确性和高效性,并对空气爆炸载荷作用下混凝土板和钢板的动力响应进行了数值模拟,数值结果与已有的试验结果以及文献报道的结论相吻合。聂源等[49]采用SPEEL高精度冲击物理显式欧拉动力学软件模拟海平面(p=101.325 kPa)上装药和在不同温度、湿度环境中的爆炸过程,得到不同温度、湿度环境下冲击波超压峰值、正压作用时间和冲量,进一步分析爆炸冲击波参数的计算模型。吴赛等[50]采用ANSYS/LS-DYNA软件建立了多组不同药量TNT的爆炸模型,并将结果与TM5-1300、Henrych以及Baker公式计算结果进行比较分析,通过多次试算分析,给出了自由空气中建立TNT爆炸模型时由比例距离选用网格尺寸的依据,分析了爆炸相似律立方根表达式的适用性及适用条件,并得到了比例距离为0.1～3.0时，自由空气中TNT炸药超压峰值的简便计算公式。

在爆炸载荷方面,主要分析其在复杂曲面结构上，时间和空间的分布特点和不同于规则曲面结构的变异性特征,但目前还缺乏详实的试验数据作为依据,可以用来指导大跨度空间结构防爆设计的外爆炸载荷模型的研究进展缓慢。

3 网壳结构数值研究进展

结构在载荷下的动力响应,只有在载荷简单、理论简化或者边界条件特殊的情况下,才可以求得解析解[51]。在实际工程中,由于网壳复杂的几何形状,通常无法通过数学解析求解获得结构的载荷和力学特性。因此,更多研究者选用数值方法来获得不同结构在不同类型载荷和边界条件下的解。近年来,爆炸载荷作用下构件或结构动态响应的数值模拟取得了重大进展。数值模拟爆炸载荷下构件或结构的动态响应克服了试验带来的一些限制；此外,高速计算技术的快速发展，使得快速、高保真的计算分析成为可能,这也促进了数值建模方面的重大进展。

目前,要对各向异性板壳结构进行静力和动力分析,最常用的数值方法是有限元方法(FEM)。FEM自诞生以来,在工程计算中一直占据着主导的地位,其应用已扩展到各个工程领域。在FEM中,连续体被分成有限数量的单元,每个单元的行为由有限数量的参数指定,整个系统作为其单元集合的解,可以根据适用于标准离散问题的程序来获得[52]。FEM可以模拟爆轰过程、爆炸波在空气中的传播[53]以及随后与目标的相互作用[54]。Carrera[55]综述了多层、各向异性、复合材料板壳结构的现有理论和有限元模型。Noor等[56]对用于预测夹层板壳结构响应的各种计算模型进行了分类。

Xiong等[57]在ANSYS软件中建立了K6型铝合金节点单层网壳的有限元模型,讨论了具有半刚性和刚性节点的K6型壳体的屈曲性能,并且根据8 000多个壳体模型的有限元计算结果,提出了带节点的铝合金板壳体弹塑性屈曲载荷的理论计算公式。Tomei等[58]在考虑几何缺陷的情况下,通过开发特定的子程序来评估自己以前提出的一些网壳结构优化方法的有效性,并对不同的案例进行了数值分析。Yan等[59]利用 ANSYS 软件对8种不同网格形式的网壳进行了几何和材料非线性分析,研究了构件屈曲与结构整体屈曲之间的相互作用。Sun等[60]利用一种基于模态能量判别准则的改进一致缺陷模态法(CIMM)，计算网壳结构屈曲载荷,其中最小的屈曲载荷就是网壳结构的屈曲能力。Zhu等[61]提出了用于非线性屈曲分析的修正一致缺陷法，用于网壳结构设计的基于机器学习的缺陷结构非线性屈曲载荷折减率预测方法。

范峰等[62]利用计算冲击载荷响应的ANSYS/LS-DYNA通用有限元软件,对135个K8型网壳算例进行了分析,得出了应力、竖向变形、网壳的塑性发展、冲击持时等重要结构响应的规律。黄明[63]运用 ANSYS/LS-DYNA建立了精细化的K8型单层球面网壳有限元模型,在外爆条件下,采用流固耦合算法进行研究,考察了炸药当量、爆炸点位置、杆件截面、矢跨比、支承条件、屋面板厚度、屋面载荷及屋面板形式等参数对结构动力响应的影响,总结出网壳结构会出现结构无损伤、局部凹陷、局部破坏、整体倒塌4种响应模式。夏明等[64]在试验数据基础上,采用 AUTODYNA 软件,建立了爆炸冲击波与140面体伪随机网壳结构相互作用的数值仿真模型,针对3种距离的空中和地面爆炸(共计6种工况),计算并分析了网壳结构的特征表面超压,得出了伪随机网壳结构的超压峰值分布规律，结果表明：作用机制由于受到结构伪随机特性的影响，与传统网壳结构相比，存在明显差异。董晓鹏等[65]利用ABAQUS有限元软件，对柱承式网架结构在连续两次爆炸载荷作用下的动力响应进行了数值模拟,提出了几种提高网架支座抗剪承载力的加固措施。翟希梅等[66]以ANSYS/LS-DYNA有限元软件为平台,建立了中心TNT爆炸载荷作用下40 m跨度的K8型单层球面网壳精细化有限元模型,研究了结构矢跨比、TNT炸药当量等对结构响应的影响,结果表明:增大结构矢跨比和屋面板的厚度,结构的动力响应程度降低。马加路等[67]基于ANSYS/LS-DYNA建立了爆炸中考虑附属结构(檩托、檩条、铆钉和屋面板)影响的40 m单层球面网壳结构有限元模型,从结构的全局响应出发,选择了网壳中节点最大相对位移和不同屈服程度杆件比例,作为单层球面网壳动力响应的衡量标准,结果表明:结构矢跨比、杆件截面、屋面板厚度和屋面活载荷对于网壳动力响应的影响程度依次降低,弹性模量等材料属性的影响可以忽略。杨帆等[68]采用显式动力有限元软件AUTODYNA对20和40 m跨度的K8型单层球面网壳,在外爆载荷下的动态响应进行了研究,将网壳结构按环数进行分区设置测点,发现单层球面网壳在外爆载荷下主要经历两次冲击波载荷,最大节点位移出现在第一次冲击载荷作用时。顾磊等[69]采用 ANSYS 有限元分析软件对单层球面网壳结构进行稳定性分析,考察了杆件初始缺陷和杆件失稳对网壳结构稳定性的影响规律；对杆件轴力和杆件失稳传导进行分析,发现网壳结构的整体破坏源于单根杆件的率先屈曲和杆件失稳的迅速传导。关博心等[70]基于多物质的任意拉格朗日-欧拉(ALE)算法,考虑下部支撑结构的作用,发现结构的最大位移并没有出现在顶点处,而是在结构的第4环,并且在结构对称方向上的节点产生的位移是不同的。

目前,使用ANSYS/LS-DYNA、AUTODYNA、ABAQUS等商用软件进行爆炸载荷下网壳结构的动态响应数值模拟分析,主要考虑结构矢跨比、TNT炸药当量、杆件截面、屋面板厚度和屋面活载荷等对结构响应的影响,此外,新型伪随机网壳结构的超压峰值分布以及考虑下部支撑结构作用的网壳结构最大位移点与一般规则网壳的动力响应存在差异。在结果和计算效率两方面,各种数值方法之间存在比较大的差异;在网壳结构防爆方面,也仅仅是提出增加防爆墙这一简单措施,而未对结构本身如何进行优化提出改进措施。

4 结论与展望

本文以网壳结构为研究对象,系统地综述了网壳结构在动载荷作用下的动态响应。首先,概述了已有的网壳结构稳定性理论研究的发展历程;其次,简单介绍了针对不同结构构件和结构整体在不同类型载荷和边界条件下应用的数值方法类型,综述了空中爆炸载荷理论分析方法的研究进展,系统介绍了爆炸载荷作用下网壳结构动力响应的数值计算方法的发展、特点及应用；最后,提出了目前研究中存在的不足以及有待进一步探索的问题,以期为网壳结构的抗爆防护设计提供参考,从而提高我国网壳结构抗毁伤能力。

1)网壳结构在爆炸载荷作用下的动态响应理论研究偏少。鉴于大跨网壳结构复杂、体型庞大,其数值计算耗时巨大,且国内外缺少网壳结构的爆炸试验结果可对目前的爆炸数值响应模拟结果进行验证,对此,开展网壳结构在爆炸载荷作用下动态响应的理论研究具有重要的意义。

2)对于一些具有特殊用途的新型空间网壳结构在爆炸载荷作用下的动态响应的研究尚未形成体系。以往的研究大都针对规则的K6、K8型网壳结构,然而,具有特殊用途的新型空间网壳结构，由于其壳面单元的伪随机分布特性,与规则网壳结构相比,二者外形迥异,无法采用面对称的简化数值模型分析计算,对其在爆炸载荷作用下的动态响应研究的文献较少。因此,开展新型伪随机网壳结构在爆炸载荷作用下的动态响应的研究,有利于提高网壳结构的抗毁伤能力,补齐短板。

3)在冲击波与破片载荷联合作用下,网壳结构动态响应作用机制尚未取得突破性研究进展。在炮弹装药质量一定的前提下,在爆炸过程中,炸药的化学能转化为冲击波爆轰产物以及破片的动能。冲击波与破片载荷联合作用下，网壳结构的毁伤机制更加复杂。如何有效提高网壳结构的抗爆能力仍是一个巨大的挑战。

4)在使用数值模拟方法对网壳结构在爆炸载荷作用下的动态响应研究中,目前主要止步于研究网壳结构的响应特征,而未对结构在防爆方面有任何改进。笔者认为,可以在数值模拟的基础上,嵌入一些软件模块,对结构进行优化设计,得到研究结构破坏响应特征的模型。