基于排队长度估计的网联车辆节能车速规划方法

张春涛，冷江昊，王博，孙超,，周星宇

（1. 北京理工大学 机械与车辆学院, 北京 100081；2. 北京理工大学 深圳汽车研究院, 广东, 深圳 518000）

车辆的节能行驶以提高车辆动力系统效率、降低行驶能耗需求为目标[1]. 非网联车辆的节能行驶方法通常关注于动力系统[2]或辅助设备[3]的优化，以在满足车辆行驶需求的前提下，降低行驶能耗. 相较之下，依托于智能交通系统的网联车辆，可以预先规划其行驶车速曲线，优化行驶能耗需求. 网联车辆通过车用无线通信技术(V2X)与智能交通系统实现信息交互，丰富的交通时空信息使得网联车辆具备了极大的节能行驶潜力[4]. 随着网联车辆的推广，节能行驶中的车速规划问题，日渐成为研究的热点问题. 基于时空交通信息对道路环境进行建模，是构建车速规划问题的关键，也将影响车速规划方法的节能效果. 根据行驶场景的差异，道路环境可分为高速道路环境和城市道路环境.

高速道路环境中，主要的影响因素包括道路坡度、车速、车流量等. LIM 等[5]以各路段的平均车速表示道路状况，构建车速规划问题；HUANG 等[6]基于宏观交通流模型和各路段的车流数据，预测各路段的交通状况，规划出能耗最优的车速曲线. 在高速道路环境中，宏观车流状态稳定，使用宏观交通流模型能够准确地对车流进行描述.

相对于高速道路环境，信号灯的存在使得城市道路环境更加复杂多变. 合理的规划车速，避免车辆在信号灯路口停车，将显著降低车辆行驶能耗[7−8].然而，仅考虑信号灯的城市道路模型过于理想化，忽略了其他车辆对路口实际通行状态的影响. HE 等[9]假设各路口的排队长度和消散时间已知，将车流排队引入为速度规划问题的约束. DONG 等[10]假设路口的排队长度已知，结合车辆动力学模型对车流排队消散时间进行了预测. 然而，直接获取排队长度对交通检测设备的分辨率、安装位置等具有较高要求，同时，夜间、雨雪、雾霾等状况下，交通检测设备的精度难以得到保证. 相较而言，目前被广泛用来采集道路车流量、车速信息的地磁线圈具有精度高、稳定性强的优点，但地磁线圈不能直接获得排队长度[11]. 在仅利用车流量和车速信息的情况下，YANG等[12−13]假设道路车流量恒定，基于冲击波理论对排队长度进行分析，得到适用于单路口和多路口的节能驾驶策略. 然而，实际交通环境中，道路的车流量是动态变化的.

由上述研究可见，对于具有连续信号灯交叉口的城市道路环境，信号灯交叉口的通行状态是车速规划问题的首要约束. 信号灯相位和排队长度是影响信号灯交叉口通行状态的两个主要因素. 然而，地磁线圈仅能检测路段的车流量、车速等数据，无法直接检测排队长度. 此外，对于信号灯控制下的不稳定车流，直接使用Lighthill- Whitham- Richards (LWR)模型和冲击波理论计算排队长度会产生明显偏差[14].因此，针对网联车辆在仅安装地磁线圈的道路环境中的节能行驶问题，如何利用获取的车流量和车速数据对动态变化的排队长度进行实时、准确地估计是一个亟待解决的关键问题.

针对上述关键问题，文中通过数据驱动的方法，构建不稳定车流条件下排队长度计算的参数化函数，对排队长度进行估计. 在此基础上，面向网联车辆在多信号灯交叉口道路的节能行驶问题，采用车流排队和信号灯联合建模的方式描述各个路口的实时通行状态，并基于车辆动力学模型，构建车速曲线规划问题；进一步地，利用提出的解耦变换求解方法对车速规划问题实现高效求解，获得参考车速曲线，引导网联车辆进行节能行驶.

1 总体架构

文中采用分层控制的方法实现网联车辆的节能行驶. 网联车辆的分层控制方法包括上层全局车速规划和下层局部运动控制. 文中的创新点集中于上层全局车速规划问题的研究中.

全局车速规划，可概括为最优控制问题的构建和求解两个步骤. 如图1 所示，根据获取的车辆状态信息和道路、交通信息构建最优控制问题的约束. 具体地，对于连续信号灯交叉口的车速规划问题，最优控制问题的约束包括车辆动力学约束、道路约束和交通约束. 其中，道路约束包括道路拓扑结构、道路限速等静态约束；交通约束主要考虑信号灯约束和车流排队约束. 车流排队具有动态变化的特性，对其准确估计是约束构建的关键. 约束构建完成后，将其和节能行驶的任务目标相结合，形成车速曲线优化问题. 在分层控制中，上层全局车速规划的输出为全局车速曲线.

图1 节能行驶方法的分层控制示意图Fig.1 Hierarchical control diagram of eco-driving

下层的局部运动控制根据安全车间距约束实时计算最大安全车速，以实现安全的节能行驶. 具体地，若某一时刻上层的全局参考车速不超过最大安全车速，则控制车辆按照参考车速行驶；若全局参考车速超过最大安全车速，则控制车辆按照最大安全车速行驶.

2 路口队列估计

2.1 参数化函数构建

根据冲击波理论，信号灯路口的排队长度由上游路段的车流状态和信号灯的红灯时长决定. LWR模型描述了稳态车流的车流量、车速、车流密度之间的关系. 应用LWR 模型和冲击波理论计算排队长度时，需将路段划分为路段微元，以保证每个路段微元内部的车流状态稳定. 这种方法需要获取各个路段微元的车流状态，对道路的智能化水平要求较高.

根据通用近似定理，神经网络可以对任意的函数关系进行拟合. 相比于反向传播神经网络，径向基神经网络具有更好的泛化性能，且具备全局逼近能力，是一种性能优越的前馈神经网络[15]. 文中采用径向基神经网络函数，对路口排队长度和路口上游车流量、车速、红灯时长之间的函数关系进行拟合. 获得不稳定车流情况下，路口排队长度的计算函数式.具体步骤为：

首先，构建用于路口排队长度估计的径向基神经网络. 径向基神经网络是一种具有“局部映射”特性的前馈网络，由输入层、隐含层和输出层构成. 文中采用高斯函数作为隐含节点的激活函数，其输出如式(1)所示.

式中：ui为隐含层第i个节点的输出；σi为高斯函数的标准差；ci为均值. 隐含层节点的输出到输出层节点的输出为线性映射关系，如式(2)所示.

式中：yk为输出层第k个节点的输出；wki为隐含层第i个节点到输出层第k个节点的权值系数；θk为输出层的阈值；n为隐含层节点数.

然后，将道路的历史车流量、车速、红灯时长数据和对应的排队长度数据作为训练数据集，对构造的径向基神经网络进行训练. 其训练过程包括自组织聚类和监督学习2 个阶段. 第1 阶段，设定隐层节点数，采用K-means 聚类算法确定各隐层节点的径向基函数的数据中心；第2 阶段，采用梯度下降法更新输出层的权值. 经比较，文中将隐层节点数设为350. 训练完成后，得到排队长度关于车流量、车速、红灯时长的参数化函数，如式(3)所示.

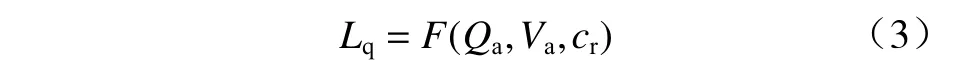
式中：Lq为最大排队长度；Qa为路段上游的车流量；Va为路段上游车流的平均车速；cr为红灯时长. 最后，利用训练得到的径向基神经网络和实时采集的路段上游车流量、车速、红灯时长数据，计算路口的排队长度.

2.2 队列估计结果

文中在SUMO 仿真软件中，随机生成了训练数据集和测试数据集，验证在不稳定车流条件下，采用径向基神经网络计算路口排队长度的效果. 具体如下：

仿真设置：一段长度为2 000 米的双车道道路，1 000米处有一信号灯交叉路口. 仿真总时长为86 400 s，等时间间隔地设置了4 种信号灯配时方案，对应的信号灯周期和红灯时长分别为(65 s, 35 s)，(90 s, 45 s)，(110 s, 55 s)，(120 s, 65 s). 在交叉口前100 m 处设置了线圈探测器，用于采集车流的车流量、车速数据；在交叉口前方200 m 范围设置了摄像头传感器，用于采集路口的排队长度；两种传感器的采样间隔均为3 min.

对于道路车流，文中做了以下假设：①两个车道的车流量大小和分布完全相同；②红灯时段产生的车流排队能够在其后的绿灯时段内完全消散；③车流中的车辆为同一类型，具有相同的动力学参数；④车辆的驾驶员类型相同，随机分配不完美驾驶系数以体现驾驶风格的差异. 设定车流的目标车速为道路限速，每个车道的车流量在[100, 1 000](veh/h)的范围内随机变化. 随机选取90%的数据作为训练集，其余数据作为测试集.

排队长度的计算结果如图2 所示. 在信号灯的控制下，整个路段处于不稳定状态，因此以整个路段作为路段微元，直接基于冲击波理论进行排队长度估计产生了明显偏差. 而径向基神经网络则表现出了良好的排队长度估计效果，其在训练数据集和测试数据集上的均方根误差（RMSE）分别为8.27 m 和9.39 m.

图2 车流排队的估计长度与实际长度对比图Fig.2 Comparison diagram of estimated queue length and actual queue length

3 节能行驶方法

3.1 车辆运动学和能耗模型

文中采用离散的车辆纵向运动学模型来描述车辆运动状态之间的关系.

式中：x为车辆的位置；v为车辆的速度；a为车辆的加速度；t为时间；∆t为采样时间间隔.

文中采用TANAKA 提出的一种电动车辆瞬时能耗计算的解析模型作为网联电动车辆的能耗模型[16]. 在此模型中，瞬时能耗被表达为速度和加速度的函数. 瞬时能耗由两部分组成：第1 部分是用于驱动车辆行驶产生的能耗；第2 部分是电机的热量损失. 总的能量损耗可根据式(6)和式(7)计算得到.

式中：r为线圈电阻；Ka为直流电机固有电枢常数；ϕ为电枢上的磁通量；N为齿轮减速比；R为轮胎半径；m为整车质量；k为风阻系数；μ为滚动阻力系数.

当车辆的加速度a(t)小于0 时，此能耗计算模型也可以表示制动能量回收的过程.

3.2 车流排队和信号灯联合建模

车辆行驶路线上存在p个信号灯，其位置用si表示，i=1,2,···,p. 文中将信号灯简化为红灯和绿灯两个相位，其持续时间分别用和表示，并规定信号灯的初始相位为红灯相位. 各信号灯初始时刻的相位偏置用表示，由此可得车辆行驶时间t与信号灯周期循环时间ci的转换关系，如式(8)所示.

式中：cT为信号灯的循环周期；mod 为取余运算. 考虑车流排队现象的存在，用附加信号灯来表示车流排队对交叉口通行状态的影响. 附加信号灯的位置由2.1 节得到的最大排队长度Lq和排队长度估计的RMSE 确定：

排队消散阶段，车流的状态相对稳定，可基于冲击波理论计算车流排队的消散速度：

式中：ω为车流排队的消散速度，对于固定的路口，消散速度可视为常数；Qc为道路最大通行能力；ρc为道路最大通行能力下的车流密度；ρd为堵塞车流密度. 根据消散速度和最大排队长度，可确定附加信号灯各相位的时间长度，如式(11)所示. 由以上对车流排队的定量估计，结合冲击波理论，可得到由车流排队产生的车辆时空禁行区域，如图3 所示.

图3 信号灯和车流排队联合建模示意图Fig.3 Joint modeling diagram of traffic queuing and traffic signal

式中：qr为附加信号灯的红灯时长，qg为附加信号灯的绿灯时长.

3.3 车速规划问题构建

节能行驶中的车速规划问题，以减少车辆能耗为主要目标，同时应兼顾车辆的行驶效率. 文中设计了包括能耗积分项和速度偏差积分项的代价函数,如式(12)所示. 其中，速度偏差积分项用于惩罚过低的行驶车速. 控制变量为车辆的加速度，状态变量为车辆的位置、车辆的速度和车辆行驶时间，控制变量和状态变量之间满足车辆动力学描述的等式约束(4)和(5). 同时，车速规划问题还需满足由信号灯和车流排队引入的不等式约束，如式(13)所示.

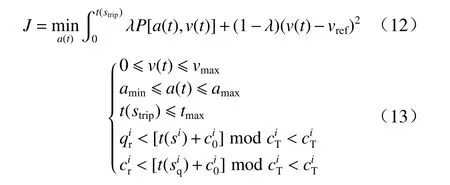
式中：vref为道路限速；λ为能耗的权重系数；strip为行程总长度；vmax为道路限速；amin和amax为最大制动减速度和最大加速度；tmax为行程最大允许时长.

3.4 解耦变换求解方法

在文中，连续信号灯路口的车速规划问题被描述为最优控制问题. 对于复杂的最优控制问题，采用多重打靶法将其近似转换为一个非线性规划问题，可以高效地获得数值解. 然而，信号灯约束表现出时空耦合的性质，破坏了状态变量可行域的连续性，使得多重打靶法的使用变得困难. 针对此问题，文中提出了一种2 阶段的车速规划解耦变换求解方法. 第1阶段，通过求解最优绿灯通行曲线，确定各路口的信号灯通行区间；第2 阶段，将连续路口车速规划问题转化为多阶段单路口车速规划问题进行求解.

第1 阶段：最优绿灯通行曲线的求解. 采用文献[17]中提出的递归搜索算法确定各信号灯路口的可通行时间窗口. 将每个可通行时间窗口离散为m个可通行时刻. 假设车辆在相邻路口间以匀速行驶，则由代价函数中的能耗积分项，可得到相邻路口间各通行时刻的转移代价函数值. 由此构建出一个“最短路径选择问题”，采用动态规划算法对此问题进行求解，得到最优绿灯通行曲线.

第2 阶段：多阶段最控制问题的求解. 基于上述得到的最优绿灯通行曲线，确定对应的各路口最优通行时间窗口. 以道路交叉口为分界点，将连续路口车速规划问题转化为多阶段车速规划问题. 获得的多阶段车速规划问题具有和原问题相同的形式. 但在每一阶段，状态变量的取值范围缩小为

时空耦合的信号灯约束被终端约束所代替：

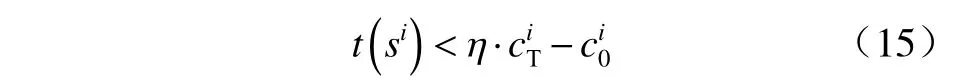
同时，附加信号灯约束解耦为

式中：η为最优通行时间窗口对应的信号灯循环周期数. 各阶段的车辆状态满足连续性约束：

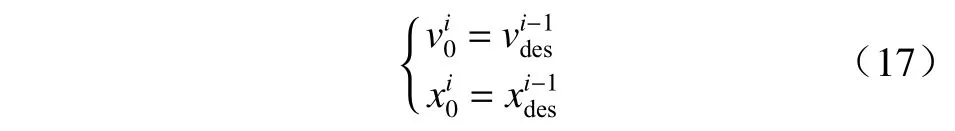
将原始最优控制问题解耦为多阶段最优控制问题后，采用多重打靶法将其转换为非线性规划问题.针对非线性规划问题，文中采用内点法对其进行求解，获得最优车速曲线.

4 仿真结果和对比分析

4.1 仿真设置

文中在SUMO 仿真软件中构建了城市道路环境，仿真道路由具有8 个信号灯路口的2 车道道路组成.差异化地设置了路口间距和信号灯相位以提高仿真场景的复杂度，信号灯的位置和相位记录在表1 中，车辆和道路参数记录在表2 中. 仿真步长△t设置为1 s，道路车流采用2.2 节中所述的车流. 如2.2 节所述，在每个路口上游设置线圈传感器，在路口前方区域设置摄像头传感器，用于采集交通数据. 在仿真过程中，基于实时车流数据，使用2.2 节训练得到的径向基神经网络估计各个路口的队列长度. 网联车辆将在不同车流强度下行驶，以检验节能行驶方法的性能.

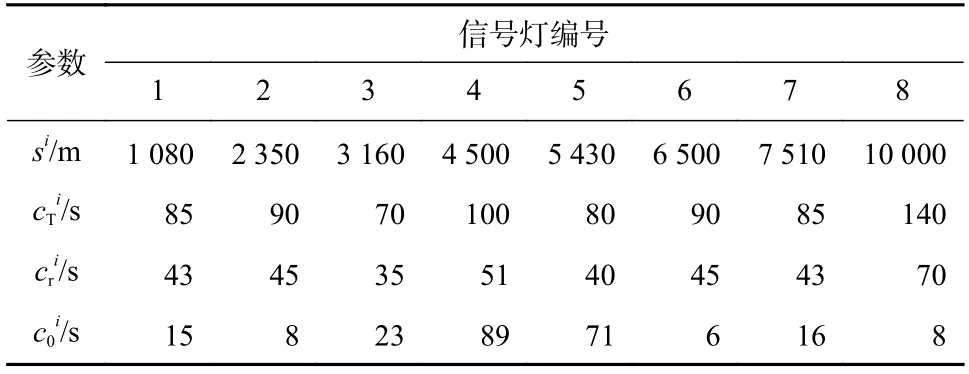
表1 信号灯的位置和相位参数Tab.1 The parameter of traffic signal

表2 车辆和交通参数Tab.2 The parameter of vehicle and traffic

对于同样的车流强度，网联车辆分别采取以下3 种车速规划方法：①以道路最大限速为参考速度，记为ECO-Baseline，为文中的基准方法；②文献[18]中采用的仅考虑信号灯的车速规划方法，记为ECOLight；③文中提出的同时考虑信号灯和路口队列的车速规划方法，记为ECO-Queue.下层的车辆运动控制均采用改进的Krauss 跟驰算法对参考车速曲线进行跟踪，同时保证车辆的行驶安全. 统计每车道的道路车流量为200、400、600、800 veh/h 时，网联车辆的运动状态. 文中中，节能行驶方法的评价指标包括：①行程能耗；②行程时间；③怠速时间；④规划次数. 为了客观地比较各种车速规划方法的性能，本研究设定：当车辆无法跟随参考车速通过当前信号灯且车速为0 时，需要对参考车速进行重新规划，并将车速规划次数作为车速规划方法的评价指标.

4.2 结果分析

4.2.1 求解稳定性分析

在不同车流强度下，分析上层全局车速规划的求解稳定性. 在一台配置了英特尔i7-9750H、CPU 基频为2.60 GHz 的笔记本电脑上，求解车速规划问题.其中，使用开源计算工具箱Openocl 对解耦得到的多阶段车速优化问题进行求解. 各阶段的控制间隔数均取50 时，车速规划问题的求解时间依次为4.25 s、5.09 s、5.74 s、4.23 s.由此可见，所提出的车速规划解耦变换求解方法具有稳定的求解时长.

图4 展示了车流强度在200～800 (veh/h)范围内车速规划问题的求解结果. 结果表明，文中所提出的车速规划方法，能够根据道路车流强度的变化，稳定地求解出最优车速曲线. 同时，基于解耦变换求解方法，顺序实现了信号灯通信区间选择，以及优化绿灯通行曲线两个目标，满足了信号灯和附加信号灯的时空耦合约束.

图4 不同车流强度下ECO-Queue 方法计算的参考轨迹Fig.4 Reference speed profile calculated with ECO-Queue method under different traffic volume

4.2.2 策略性能对比

在不同车流强度下，采用不同上层车速规划方法时，网联电动车辆的各项性能评价指标如下表3和表4 所示. 由表3 可见，相比于ECO-Baseline 策略，由于考虑了信号灯约束，ECO-Light 策略降低了2.98%～35.39%的行驶能耗. 随着道路车流强度的增强，ECOLight 策略的节能效果逐渐衰减. 而在应用ECO-Queue策略时，得益于对车流排队的充分考虑，节能行驶方法适应了实时变化的路口通行状态. 相比于ECO-Light策略，ECO-Queue 策略不仅降低了40%以上的能耗，同时，能耗消耗量在不同的车流强度下较为稳定.

表3 行程能耗和行程时间Tab.3 Consumption and trip time

表4 怠速时间和规划次数Tab.4 Idling time and planning counts

如表3 和表4 所示，相比于ECO-Baseline 策略，ECO-Light 策略和ECO-Queue 策略的行程时间略微提升.ECO-Light 策略和ECO-Queue 策略的目标是通过实现车辆的无怠速行驶，保证车辆的行驶效率. 如表所示，在无车流的理想环境中，两种方法均实现了无怠速行驶. 但在车流强度逐渐增强的过程中，由于ECO-Light 策略未考虑车流排队的延误影响，车辆在实际行驶过程中的怠速时间大幅增加，极大降低了车辆的行驶效率. 相比之下，在仿真环境中，ECOQueue 策略始终可以实现无怠速运行，保证了车辆的通行效率.

由表4 可见，由于ECO-Light 策略未充分考虑车流排队的影响，使得下层局部运动控制难以跟踪参考速度轨迹. 当车辆由于车流排队的延误，导致在下游信号灯路口停车时，原参考车速曲线已无参考价值，需要重新进行车速规划. 相比于ECO-Baseline 策略，ECO-Queue 策略可以显著减少重规划任务的执行次数，提高节能行驶方法的鲁棒性.

4.2.3 行驶曲线分析

下面以每车道的车流量为600 veh/h 时，网联电动车辆分别采用ECO-Light 和ECO-Queue 两种策略的实际行驶曲线为例，对文中所提出的节能行驶方法进行进一步分析.

如图5 所示，ECO-Light 策略根据信号灯位置和时序信息生成了参考车速曲线. 尽管理论上该曲线可以引导车辆在绿灯时段通过各个信号灯路口，但由于车流排队的存在，车辆需在路口前方制动以保持安全的车间距，从而产生减速行为，偏离参考车速曲线，且增加了能量消耗. 在使用ECO-Queue 策略时，充分考虑了车流排队的影响. 因此车辆能跟随规划出的参考车速曲线平稳地通过各个信号灯路口. 尽管由于排队长度的估计误差导致车速产生了微小波动，但ECO-Queue 策略依旧展现出更好的节能行驶效果.

图5 不同车速规划策略下的位置和车速曲线Fig.5 Position and speed profile with different speed planning method

如图5 所示，在使用ECO-Light 策略时，规划阶段输出了较为激进的参考车速曲线. 但由于车流排队延误影响的不断累积，车辆无法跟随参考车速曲线在相应的信号灯通行区间通过路口. 车辆在路口的停车，导致了参考车速曲线失去引导作用. 此时，必须重新进行车速规划，以更新参考车速曲线. 如图所示，从车辆出发时刻起，ECO-Light 策略执行了3次车速规划. 相比之下，得益于对道路环境更充分的建模，ECO-Queue 策略增强了节能行驶方法的鲁棒性. 对于图示的短距离行程，仅进行1 次车速规划即可引导车辆平稳到达终点.

5 结 论

本研究考虑车流动态变化的城市道路环境，提出了一种基于排队长度估计的节能行驶方法. 基于数据驱动的方法构建了用于排队长度计算的参数化函数(径向基神经网络)，提升了不稳定车流条件下排队长度估计的准确性；基于车流排队和信号灯的联合建模，构建了适应不同车流强度的最优控制问题；基于全局优化方法和多重打靶法设计了车速规划问题的解耦变换求解方法，保证全局优化性的同时，降低了问题的计算复杂度. 仿真结果表明，相比于未考虑车流排队的节能行驶方法，文中所提出的结合宏观交通信息的节能行驶方法具有更好的节能效果，并显著增强了节能行驶方法的鲁棒性. 本研究中的节能行驶方法可应用于智能交通系统覆盖范围内的网联车辆，提高其行驶经济性.