某埋头式弹丸动态冲击挤进特性的研究

常人九，薛晓春，余永刚

（南京理工大学 能源与动力工程学院，江苏，南京 210094）

埋头弹药是一种采用特殊装药结构的新型弹药，弹丸全部缩在药筒内部，整体呈标准的圆柱状，其对于提高武器系统结构紧凑化和威力都具有重要的意义[1]. 但是埋头弹药的特殊结构也使弹丸发射过程发生了重大变化，传统火炮弹丸初始嵌入膛线时速度很小，而对于埋头弹武器，弹丸前期需在药筒内自由滑动一段距离，至弹带接触身管起始部止，在嵌入膛线时已经具有相当大的速度. 因此，埋头式弹丸挤进坡膛过程是一个极其复杂的强动态冲击过程，涉及到弹带材料塑性大变形及接触面的复杂受力现象，且行程和时间都很短，试验可直接测量的参数非常有限. 目前，埋头弹内弹道理论仍是基于瞬时挤进等基本假设将其简化处理，可较好地指导工程实践. 随着现代化武器的发展，弹带挤进过程对于火炮内弹道性能都有显著影响，然而，由于目前瞬时假设简化了弹丸克服拨弹力后挤入膛线前的复杂运动过程，瞬时挤进理论难以准确描述埋头式弹药动态冲击挤进过程，因此需要进行埋头式弹药的动态冲击挤进过程的研究.

已有较多针对传统弹丸挤进过程的研究，但是针对埋头式弹丸的动态冲击挤进过程的研究较少.吴志林等[2]采用关于弹丸挤进阻力的线性函数，数值研究了双头弹初始挤进阻力及最大挤进阻力对弹头初速和最大膛压的影响规律. 王育维等[3]引入了弹带挤进阻力关于弹丸行程的分段线性函数，建立了某大口径火炮两相流内弹道模型. 段吉员等[4]计算了某口径平衡炮的弹带挤进压力，并将挤进时期内弹道诸元与忽略挤进过程的内弹道诸元进行了对比，重点分析了弹带挤进时期的内弹道特性. 彭志国等[5]对火炮坡膛涂油条件下的弹带挤进状态进行了分析，并计算得到了弹带挤进摩擦因数表达式. 邱从礼等[6]针对某火炮弹炮配合后弹丸存在较长自由行程的特点，建立了弹丸挤进阻力的计算模型.TAO[7]将弹带变形阻力公式耦合到弹丸挤进时期的运动方程中，建立了考虑弹带挤进过程的内弹道数学模型.孙河洋等[8]考虑了经典内弹道方程组和弹带挤进过程的耦合效应，借助显式非线性有限元算法对不同坡膛结构下弹带挤进过程进行了数值模拟. 丁传俊等[9]建立了弹炮热力耦合有限元分析模型，采用显式有限元方法对弹丸挤进过程及随后的内弹道过程进行了数值模拟，且通过与试验结果的对比，验证了模型的准确性. 孙全兆等[10]建立了弹带挤进坡膛的有限元模型，通过数值模拟研究了弹带变形及刻槽形成过程，并分析了弹带动态挤进阻力变化规律. 李淼等[11]将弹丸起始运动内弹道方程的解作为边界条件，利用显式方法对弹带挤进过程进行了热力耦合计算. 曹学龙等[12]采用有限元方法建立了包含坡膛的全身管模型，数值分析了弹带变形过程和弹丸膛内运动规律. 邹利波等[13]建立连续挤进模型，分析了单发或连发条件下坡膛的受力磨损情况，以上述各位学者主要通过对各个工况下的常规弹药的挤进过程进行有限元分析，并总结出其挤进阻力的相关变化规律. 对于埋头式弹药的研究仅通过内弹道方程组来研究其性能，并将挤进过程简化为瞬态冲击. 为了能更加准确描述其挤进时期对内弹道性能的影响，本论文针对埋头式榴弹，在借鉴常规式弹药挤进分析方法基础上，构建了弹带动态挤进过程中的高冲击、强摩擦和大变形接触的有限元模型，并通过与相关试验结果对比，验证了模型的有效性. 然后，结合埋头弹药二次点火及火药程序燃烧的特殊性，数值研究了埋头式弹丸冲击挤进过程中的应力变化特性及弹带刻槽形成机理.

1 物理模型

1.1 发射系统结构

埋头弹药主要由底火、中心传火管、主装药、速燃药、可燃导向筒、弹丸及药筒等部分组成，如图1所示. 底火位于埋头弹底部，弹丸位于药筒前部的可燃导向筒中，在弹丸底部放有少量速燃药，速燃药与底火之间通过中心传火管连接，主装药分布在传火管与导向管的四周. 埋头弹与常规弹药的最大不同之处在于，埋头弹药的发射装药和弹丸是一个整体，弹丸位于药筒中，可在导向筒内自由滑动，通过设计合理的装药结构，可保证弹丸入膛动作的准确性与可靠性.

图1 埋头弹药结构示意图Fig.1 Diagram of buried ammunition structure

埋头弹药发射系统的理想工作状态是：底火击发后先点燃速燃药（一次点火），速燃药燃烧产生的气体推动弹丸沿可燃导向管自由滑动，并同时点燃可燃导向筒和部分主装药，待弹丸嵌入膛线时，可燃导向筒完全破裂，主装药被全面点燃（二次点火），产生的燃气推动弹带挤入坡膛，并继续沿身管运动. 也就是说，弹带在嵌入膛线时，弹丸先期已在药筒内自由滑动一段距离. 因此，弹带会以一定的一次上膛速度，在弹底压力的作用下动态冲击挤入坡膛，本文研究的对象为某40 mm 埋头式榴弹，弹带为紫铜材料，坡膛锥度由2 段组成：第一段的锥度为1/17.60，第二段的锥度为1/17.33，膛线采用24 条等齐膛线，深度为0.6 mm.

1.2 埋头式弹丸冲击挤进过程

由于埋头弹药采用的是二次点火和火药程序燃烧的新原理，因此，其挤进过程与普通弹丸存在较大的差异，图2 为本文所研究的某40 mm 埋头式榴弹在一次点火的先期作用下，弹带起始嵌入坡膛时的相对位置图. 此时，弹丸已经具有一定的速度u0，弹带凸台与坡膛紧密接触，可燃导向筒已完全破裂，主装药被全面点燃，弹丸开始以一次上膛速度u0与弹底2 次点火燃气压力综合作用下，克服挤进阻力向前挤进运动，弹带在膛线和身管的挤压下发生弹塑性变形产生凹槽，待弹带全部挤进身管膛线，整个挤进过程结束.

图2 挤进开始时弹带与坡膛的相对位置示意图Fig.2 Schematic diagram of the relative position of the cartridge belt and the slope bore at the beginning of engraving

2 有限元计算模型

2.1 基本假设

由于弹带挤进坡膛时其塑性变形很大，受力情况十分复杂，所涉及到的影响因素也较多. 因此，在考虑挤进动力学过程主要特点的基础上，作出如下基本假设：

①初始时由弹带凸台与坡膛接触定位，假定弹带的初始应力和初始变形为0；

②对身管和弹体施加刚性约束，仅考虑弹带材料变形，忽略身管和弹丸本体的应变；

③不考虑弹丸的动不平衡，假定弹丸质心与身管的轴线共线；

④不考虑挤进过程中身管的后座运动、忽略弹丸前端空气阻力及重力;

⑤假定弹丸与身管没有热交换，挤进过程中弹带材料的变形是绝热过程.

2.2 有限元网格模型

以某40 mm 口径埋头弹火炮坡膛及榴弹、紫铜弹带为研究对象，采用有限元前处理软件建立8 节点六面体的三维有限元实体模型，如图3 所示. 划分网格时采用网格扫掠法，由于弹带是挤进成形的关键部位，对其进行加密处理，多次计算结果表明弹带单元网格大小为0.2 mm，弹丸和身管单元网格大小分别为0.8 和0.5 mm，整体模型网格数量为232 795，弹带网络94 240 时，可以保证计算精度且计算时间较少. 由于本文重点研究弹带挤进坡膛的过程，因此在建立身管模型时，采用了截短身管模型.

图3 身管及弹带有限元网格Fig.3 Body tube and bullet band finite element mesh

2.3 材料模型

本文研究的榴弹弹带材料为紫铜，为了描述其在挤进过程中出现的大塑性变形、损伤、应变硬化、应变率硬化及温度软化等现象，引入了Johnson-Cook本构关系模型. 该模型是一个经验性的黏塑性模型，是由JOHNSON 和COOK[14]在1983 年提出的，用于解决高应变率和高温问题上的材料本构关系，包括了用以描述塑性变形和断裂过程的Johnson-Cook 塑性模型及损伤失效模型[15].

Johnson-Cook 塑性模型为应变–应力关系，可表示为：

式中：σ为von Mises 屈服应力；A为准静态实验下的屈服强度；B、n为应变强化参数；C为经验性应变率敏感系数；m为温度软化指数； εp为 等效塑性应变；ε∗为量纲一等效塑性应变率；T*为相对温度，通过下式可求得：

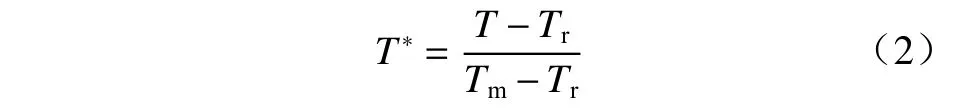
式中：Tr为参考温度（一般为室温）；Tm为材料的熔化温度.

弹带材料模型的断裂与失效由下列累计损坏法则判定：

式中Δε为加载过程中有效塑性应变增量.

Johnson-cook 初始损伤准则中通过等效塑性应变εf定义初始损伤：

式中：应力三轴度 σ∗=p/σeff，其中p为静水压力，σeff为等效应力；d1～d5为Johnson-Cook 模型中相关计算的紫铜材料常数，反映了应力三轴度、应变速率以及温度对材料失效的影响，由实验仿真拟合测定. 当D=1 时则判定材料此时已经发生断裂失效，仿真计算中通过对材料单元的删除来模拟失效. 本文所涉及的紫铜材料，其Johnson-Cook 模型的各参数[13]如表1 所示. 且由于主要研究弹带的变形过程，因此将弹体与身管模型设置为刚体模型，其材料采用炮钢材料各参数[16]如表2 所示.

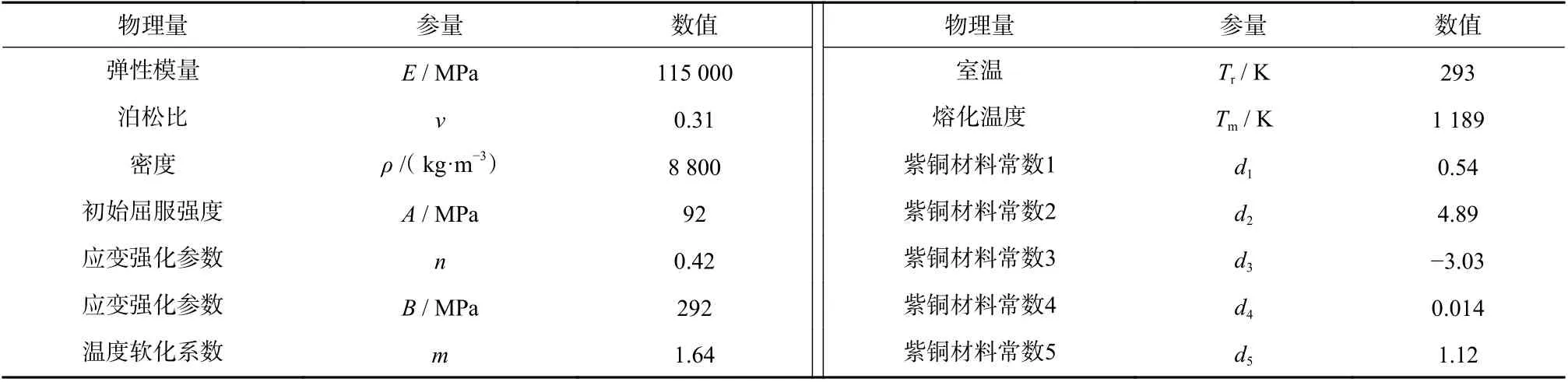
表1 紫铜材料本构模型参数Tab.1 Constitutive model parameters of copper materials

表2 炮钢材料本构模型参数Tab.2 Constitutive model parameters of steel materials

2.4 Mie-Gruneisen 状态方程

由于弹带的挤进过程是一种金属材料在高温、高压、高应变率条件下的材料动态行为，弹带运动过程中静水压的变化则通过Mie-Gruneisen 状态方程来描述.

当材料受压缩时，其静水压力为

式中：c为体积声速；S1、S2、S3为曲线的斜率系数；γ0为Gruneisen Gamma 系数；α为对γ0的一阶体积修正；E0为初始单位动能；ρ0为材料初始密度.

2.5 初始边界条件

埋头式榴弹的紫铜弹带与坡膛之间定义为面–面侵蚀接触，采用库伦模型描述其摩擦作用，动摩擦因数取0.1. 而紫铜弹带与弹体之间为自动接触，将紫铜弹带固定在弹体上. 同时，对身管采用全自由度约束，仅允许弹丸沿身管轴线方向平动与转动. 将试验测得的弹底燃气压力作为动载荷施加于弹丸底部，提供弹丸向前运动的动力. 由于埋头式弹丸的特殊性，在挤进开始时就有一定的速度. 因此，结合内弹道方程组，内弹道参数如表3 所示，并带入计算，得到弹丸开始挤进时期的初始速度为25 m/s，并加载于弹体和紫铜弹带上.

表3 内弹道相关计算参数Tab.3 Internal ballistics related calculation parameters

3 冲击挤进过程的数值模拟结果及分析

运用LS-DYNA 动力显式(dynamic explicit)求解器对上述有限元模型进行仿真分析. 求解器采用了拉格朗日算法显示求解. 并基于单元方程式与沙漏控制，避免计算过程中产生的单元网格畸变问题.

3.1 计算方法可靠性验证

为了验证仿真计算模型的可靠性，本文将某40 mm常规榴弹模拟挤进实验结果与使用该模型进行同样条件挤进过程的计算结果进行对比. 图4 为本次实验所采用的Phantom v710s 型高速摄影仪，实验中利用该高速摄影系统对弹丸在挤进过程中的位移变化进行了记录，如图5 所示，并采用压力测试系统获得了挤进时期膛内压力的变化规律. 同时将实验测得的坡膛处压力作为验证计算时的初始边界条件，采用上述已建立的有限元模型对本次常规弹药的模拟挤进实验进行数值模拟.

图4 高速摄影仪器Fig.4 High-speed photographic instrument

图5 实验过程图Fig.5 Experimental process diagram

图6 和图7 分别为挤进时期弹丸行程的数值仿真及挤进结束后弹带形态与实验结果对比图. 通过对实验过程分析可知，弹丸在15.3 ms 开始运动，即在15.3 ms 时弹底压力达到其起动压力，而在17.0 ms弹丸已经进入身管全深膛线，完成了挤进过程. 所以，选择从15.0～17.0 ms 处取值进行实验与仿真计算结果的对比. 由图6 可见，两者位移变化的一致性较好，15.2 ms 时，弹带开始出现变形，弹底压力大于弹丸受到的阻力，弹丸开始沿身管轴线挤入坡膛，16.0 ms时，弹丸速度显著提升. 整个时间范围内，数值计算与试验得到的弹丸位移最大误差出现在17.0 ms，其相对误差为5.06%，产生误差的原因有以下几点：①弹丸位移是通过高速摄影拍摄弹丸前端刻度后，图像处理得到，可能存在人工测量误差；②实验时炮膛内润滑导致实际摩擦因数与仿真存在一定误差；③弹带材料强度实际与理论值存在一定误差. 综上，最终导致仿真结果稍低于试验结果，但在误差允许的范围内，且由图7 可知，挤进完成后的弹带形态与实验也相同，因此，所采用的计算模型能够较为准确预测弹丸挤进过程.

图6 位移对比图Fig.6 Comparison diagram of displacement

图7 挤进完成后弹带变形对比图Fig.7 Comparison chart of the deformation of the projectile belt after engraving is completed

3.2 弹带变形及刻槽形成规律分析

在上一节计算模型验证的基础上，本节采用相同的计算模型以某40 mm 埋头式榴弹的试验弹底压力和弹丸一次上膛速度作为模型初始边界条件进行实际射击条件下埋头式弹丸动态冲击挤进过程的数值仿真. 图8 为埋头式榴弹弹带变形应力云图，从中可以看到弹带变形形态以及刻槽的形成过程.

图8 埋头式弹丸弹带变形应力图Fig.8 Deformation stress diagram of projectile belt at deceleration stage of projectile

由于埋头式弹药结构的特殊性，其挤进运动过程与常规弹丸也有明显差别，由图8 可知，埋头式弹丸的挤进过程可分为3 个阶段：在0～0.9 ms，处于挤进初期，该阶段可燃导向筒还未完全破裂，弹丸主要以一次点火后期获得的初速度冲击挤进坡膛，弹带一端受到坡膛内壁面挤压，表面应力超过其屈服强度92 MPa，产生塑性变形，至0.9 ms 时，部分弹带已进入膛线起始部，由于膛线起始部的阳线凸出量逐渐变大，因此这部分弹带与阳线接触位置需不断发生大变形才能挤入膛线，导致其受到的应力也逐渐增加，最终弹丸速度下降至0；在0.9～1.5 ms，处于挤进中期，由于该阶段为二次点火初期，主装药燃气作用下弹底压力还不足以克服挤进阻力，弹丸处于停止阶段；在1.5～2.3 ms，处于挤进后期，该阶段主装药全面燃烧，火药燃气推动弹丸开始加速冲击挤入坡膛，弹带与膛线接触部分随着阳线凸出量的增加而逐渐产生大量塑性变形，并最终失效形成刻槽；2.3 ms后，弹带完全挤入身管全深膛线，挤进过程结束.

为了深入探究紫铜弹带在冲击挤进时期的刻槽形成机理，分析了材料在塑性大变形之后的断裂失效模式与相关特征点应力应变量的变化. 图9(a)与图9(b)分别为2.2 ms 时，弹带材料的内部应力三轴度和内部Lode 参数云图，其中应力三轴度可反映出弹带所处的应力状态，而Lode 参数为排除球形应力张量对塑性应变的影响，从而反映应力特征的参数，通过观察用来考虑应力状态对韧性断裂的影响[17].

由图9(a)和图9(b)的弹带中部横切面参数云图可知，紫铜弹带直接受膛线冲击挤压摩擦的区域应力三轴度均小于0，而Lode 参数主要小于0 或者接近于0，这就意味着弹带在挤进过程中，其表面材料发生断裂失效的模式主要是以剪切失效为主. 而弹带前端面及弹带凸起处表层区域的应力三轴度大于0，表明该区域由于摩擦阻力的作用，弹带材料受到了与膛线切向方向相反的拉伸作用. 从弹带刻槽纵切面的参数云图可看出，该区域应力三轴度大都处于小于0 的状态，Lode 参数几乎都接近于0，也就是说该区域弹带材料主要是处于被压剪的状态.

图9 埋头式弹丸弹带内部变形参数云图Fig.9 Cloud map of internal deformation parameters of countersunk projectile belts

图10 为纵向特征点应力、应变关系图，如图10（a）所示，a、c、e3 点为弹带刻槽处纵向特征点，b、d、f为弹带非刻槽处纵向特征点. 由图10（b）与图10（c）可知，初始时刻，弹带表面受挤压，a、b2 点应力上升，且应力波传播，导致内部c、d、f、e各点应力也不断上升. 然而，由于f、d点位于弹带非刻槽处，因此其应力快速下降至0. 且随着弹带不断挤入坡膛，表面一层逐渐失效被切除，因此a、b2 点应力在后期始终为0，而c、d、f、e点应力、应变值整体呈现出升高的趋势，由于d、f点位于弹带非刻槽位置，因此其应力值在后续变化较小，而c、e2 点应力最终也下降至0，表现为被身管阳线刻蚀形成刻槽.

图10 纵向特征点应力及应变曲线Fig.10 Longitudinal landmark stress and strain

综上分析，可进一步得到弹带材料在冲击挤进时期的变形与刻槽形成机理. 即：起始弹带以一定初始速度冲击坡膛，期间弹带部分受坡膛挤压，且随着其表面应力的增大，经过弹性与塑性变形后，进入膛线起始部. 之后在二次点火作用下，主装药燃气不断产生，弹底压力升高，推动弹丸向前运动，弹带材料与阳线接触部分逐层以剪切失效形成刻槽，其一部分材料被阳线推到弹带后方，另一部分被挤入阴线.

4 弹丸冲击挤进过程的阻力特性分析

图11 和图12 分别为仿真模拟计算得到的冲击挤进过程中埋头式榴弹的位移、速度、加速度及弹带冲击挤进阻力随时间变化的曲线图. 其中弹丸冲击挤进阻力是利用牛顿第二定律，由弹底压力、弹丸挤进加速度及弹丸质量计算得到.

图11 内弹道参数曲线图Fig.11 Internal ballistics parameters curve

图12 弹带挤进阻力曲线图Fig.12 Curve of resistance to belt engraving

由图12 可知，在挤进过程中，弹丸首先以一次点火时期可燃导向筒的速度25 m/s 开始挤入坡膛，此时弹带表面发生非常大的变形量并逐渐损伤失效，因此挤进阻力增加，且该挤进阻力远大于弹底压力，从而导致弹丸挤进加速度为负值，挤进速度不断降低直至0，弹带挤进的变形速率也降低，而挤进阻力又包含了由材料变形产生的阻力. 因此，挤进阻力也逐渐降低. 当弹丸速度下降为0 时，其行程达到了10.7 mm.之后，弹丸进入停止运动阶段，弹丸挤进阻力基本保持不变. 但是，随着主装药的不断燃烧，弹底压力快速增加，弹带开始不断冲击坡膛，并发生大变形、损伤失效，因此挤进阻力在这个过程中又逐渐增加. 但在1.6 ms 时，弹底压力大于弹丸挤进阻力，弹丸再次加速冲击挤入坡膛. 由于该过程中，弹底压力上升较快，弹丸加速度也上升很快，膛线开始快速刻蚀弹带. 随着弹丸逐渐挤入身管全深膛线，弹带变形量逐渐减小，弹丸挤进阻力也逐渐减小. 由此可知，弹丸最大冲击挤进阻力并不出现在弹带完全挤入身管全深膛线的时刻，而是在弹带开始出现大变形与损伤失效的过程中.

采用高斯公式对弹带冲击挤进阻力曲线进行拟合，图12 为拟合后的阻力曲线图，为能够得到更好的拟合结果，对曲线采用了分段拟合的方法，拟合公式如下：

可决系数R2用于测定多个变量之间关系密切程度的指标，其值越大表明拟合曲线的拟合程度越强，用以下公式计算为

式中：F为根据拟合方法所采用的回归方程计算出的估计值；为样本平均值.

计算得出2 条曲线的R2值分别为0.979 17 和0.915 22，说明其拟合公式能够很好地表示阻力与时间之间的数学关系，可以应用于此工况下埋头式榴弹内弹道参数计算.

5 结 论

通过建立埋头式榴弹动态冲击挤进过程的三维有限元模型，并采用Johnson-Cook 本构关系模型描述其中紫铜弹带材料的大塑性变形、损伤、应变硬化及温度软化等现象，揭示了弹带材料的变形规律及断裂失效模式，并分析了埋头式弹丸冲击挤进过程的阻力特性，得到如下结论：

①通过对比某40 mm 常规榴弹挤进过程的数值计算与试验结果，得到两者的最大位移相对误差为5.06%，在误差允许的范围内，验证了仿真计算模型的正确性，说明所建立的数理模型能够准确预测埋头式榴弹的动态冲击挤进过程.

②埋头式弹丸的冲击挤进过程主要分为3 个阶段：初期的减速冲击挤入坡膛阶段，该阶段弹带表面的应力不断上升，经历了弹性变形到塑性变形的过程并产生损伤失效，且在挤进阻力作用下弹丸速度逐渐降低至0；弹丸静止阶段，该阶段弹底压力还不足以克服弹带挤压变形与摩擦阻力，弹丸处于静止状态；后期的加速冲击挤入坡膛阶段，该阶段随着主装药不断燃烧，弹底压力大于弹丸挤进阻力，弹带再次加速冲击挤入坡膛，并在相应区域逐层剪切失效形成刻槽. 当紫铜弹带完全挤入身管全深膛线时，整个动态冲击挤进过程结束.

③埋头式榴弹在冲击挤入坡膛过程中，挤进阻力呈现出强烈的非线性变化规律，在起始冲击挤进坡膛时，弹丸初速度较大，弹带发生变形，冲击挤进阻力增加，但是随着弹丸逐渐挤入身管全深膛线，弹带变形量逐渐减小，弹丸冲击挤进阻力也逐渐减小.

④运用高斯公式对计算所得的阻力与时间的关系进行拟合，并引入可决系数对所拟合出的曲线进行判定，获得了阻力与时间之间的计算公式，可以用于指导埋头式榴弹内弹道及装药结构设计.