基于有限测点的铝合金板残余应力场重构研究
刘广彦,熊土林,王璐,文磊
(1. 北京理工大学 宇航学院,北京 100081;2. 北京科技大学 国家材料服役安全科学中心,北京 100083)
机械加工过程会引起残余应力,而残余应力会对构件的力学性能产生重要影响[1],例如它可能会降低构件屈服极限[2],缩短构件疲劳寿命[3],造成应力腐蚀开裂[4]等. 因此消除残余应力通常对提升构件的力学性能具有重要意义,而了解构件内部残余应力场分布对去应力加工起着关键的作用. 残余应力可通过无损测量法或有损测量法[5]获得. 无损测量法在不破坏构件的情况下通过物理手段来获取其残余应力,例如X–射线衍射法、同步辐射法等. 有损测量法则是通过对构件施加机械破坏,根据构件变形的重新分布计算出残余应力,例如钻孔法、剥层法等. 然而上述残余应力测量方法只能获得构件有限测点的残余应力值,无法获得全场残余应力分布,发展一种根据有限测点的残余应力值重构构件全场残余应力分布的方法具有重要的应用价值.
构件全场残余应力可通过插值法[6]、有限元模拟[7−8]等方法获得,但插值法本质上是一种数学方法,未考虑残余应力分布需要满足的物理属性;而有限元模拟在实际工程中由于缺乏对加工工艺的深入了解会导致较大的残余应力预测误差. 发展从有限实验测点值重构出带有力学约束的残余应力场的方法在过去10 年受到广泛关注[9]. JUN 等[10]提出了本征应变法重构全场残余应力,该方法通过求解满足平衡方程、物理方程的本征应变场从而重构出构件残余应力场. 在本征应变法基础上, COULES 等[11],CHUKKAN等[12]还开发了一种平滑逆本征应变方法,用于由有限应变测量结果重建残余应力场,从而抑制了与问题物理规律相反的波动. 然而本征应变法需要预先知道构件本征应变的分布区域,否则重构复杂的残余应力场将变得十分困难. 一种可替代的重构方法是应力函数法[13],应力函数法通过构造满足平衡方程、边界条件的应力函数重构残余应力场. FARRAHI等[14]使用应力函数法重构了厚壁圆筒的残余应力场. FAGHIDIAN 等[9]使用修正应力函数法重构了不同深度位置处受喷丸工艺影响的三维喷丸板残余应力. 王凤云[15]利用傅里叶级数形式的应力函数对四点弯试件的残余应力场进行了有效重构. 然而,由于残余应力的分布具有高度的非线性,不同工艺下的残余应力场往往需要不同的应力基函数表达. 此外,由于难以构造合适的基函数,现有应力函数法大多仅限于一维残余应力的重建,即只能得到构件沿某一特定方向的残余应力分布,针对构件真实复杂残余应力场重构的应力函数法目前文献中还报道较少.
为了改善应力函数法的上述不足,本文发展了一种更为有效的残余应力场重构方法,即选择双元傅里叶函数作为应力函数逼近任意残余应力场分布规律,通过优化算法反向识别应力函数中的未知参数. 提出的方法可通过模型阶数确定重构残余应力场需要的测点个数,避免了测点选择的盲目性,在预测复杂残余应力分布方面具有通用性. 需要指出的是在工程实际中应用本文的方法进行预测时,由于满足有限测点的残余应力场并不唯一,为了提升重构残余应力场的精度,确定模型阶数可能需要一定的经验以避免重构场的过拟合或者通过补充测点等策略解决过拟合问题.
1 残余应力场重构理论
1.1 应力函数法
物体的残余应力在没有外力和热梯度情况下保持自平衡状态[16],残余应力应当满足平衡方程:

物体的自由边界上不存在面力,因此残余应力满足边界条件:

式中l、m和n为边界外法线方向余弦,如在垂直于z轴的表面上,有

将式(3)带入式(2)中,求解方程可得:

联立式(1)(4)可得:

对于平面问题,为了满足平衡方程(5),可引入艾瑞应力函数 φ(x,y),应力分量与应力函数的关系为

现有文献中使用1 个应力函数来同时表征3 个应力分量( σx、 σy、 τxy)的研究还鲜有报道,这主要是由于很难找到1 个合适的应力函数使得所有应力分量同时满足实测散点残余应力,以及平衡方程和边界条件给定的力学约束.
应力函数是解析函数,可用三角级数的展开式来表达,本文选取双元傅里叶级数来表示艾瑞应力函数,可逼近任意复杂的应力分布形式:
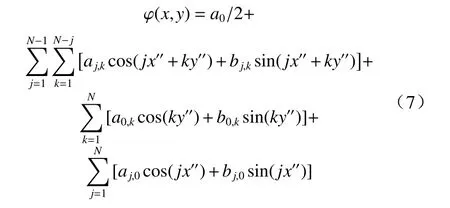
式中:N为用来预测残余应力场需要的模型展开项数,称为模型阶数;aj,k、bj,k(j,k=0,1,···,N)为待确定的未知系数;x′′、y′′为 [0,π]范 围内的独立变量,且x′′=π(x−xmin)/(xmax−xmin),y′′=π(y−ymin)/(ymax−ymin),其 中xmin、xmax分 别 为x坐标的最小值 和最大值,ymin、ymax分别为y坐标的最小值和最大值.
将式(7)带入式(6),可得:

为了求解残余应力,首先需要确定应力分量表达 式 中 的 未知 参 数. 由 式(8)~(10)可 知 σx、 σy和τxy分别包含N2+N、N2+N和N2−N个待确定参数. 确定未知参数的过程是一个反问题,可通过优化算法使目标函数最小化而获得. 目标函数反映的是重构残余应力与真实测点残余应力的误差关系,定义为:

1.2 确定模型阶数
通常构件上的残余应力不能被充分测量,由式(8)~(10)可知,未知参数的个数随着模型阶数N增大而显著增多,因此选择合适的模型阶数很关键. 为了得到合适的模型阶数,引入判定系数R2:

判定系数是用来衡量回归拟合程度的度量,取值范围为0≤R2≤1,数值越接近1 代表拟合程度越高.模型阶数可通过求解不同N与对应的R2关系,然后选择使判定系数趋于1 的阶数来确定.
2 残余应力场重构方法验证及应用
2.1 三点弯试件模拟残余应力场重构
图1 为理想弹塑性材料三点弯有限元模型,模型尺寸为100 mm×20 mm. 有限元模型在ABAQUS 软件中被离散成2 000 个4 节点四边形单元(CPS4R),单元尺寸为1 mm×1 mm. 模型下端左右两侧为支撑刚体;中间顶部为刚体加载柱,用于施加外载荷. 梁的弹性模量为70 GPa,泊松比为0.3,屈服强度为300 MPa.通过对模型施加大小为2 500 N 的集中力使其发生塑性变形,完全卸载后模型内仍存在应力场(图2),本研究将此应力场作为三点弯试件的残余应力场验证应力函数重构法的有效性.

图1 三点弯试件有限元模型Fig.1 Finite element model of three-point bending specimen

图2 三点弯试件模拟残余应力场Fig.2 Simulated residual stress field of three-point bending specimen
为了确定式(7)中合适的模型阶数,本研究首先对有限元模型(图1)中A-A线和B-B线上的残余应力进行了重构. 从A-A线和B-B线上均匀选取53 个测点数据,通过优化算法使其式(11)最小化,图3 所示为A-A线和B-B线残余应力重构的R2-N图,该图表明当模型阶数N≥10 时,R2趋于平缓,且R2≥0.95,因此该模型选择N=10 作为模型阶数. 图4 所示为AA线和B-B线上残余应力的重构结果,可以看出重构残余应力与真实残余应力分布较为一致.

图3 模型阶数与判定系数关系Fig.3 Relationship between model order and determination coefficient
从图2 可知三点弯试件的残余应力主要分布在中间对称位置附近,其余位置残余应力非常小或接近0. 本文选择了对图2 中数值较大的黑色虚线框内的残余应力场进行重构,重构区域包含420 个节点.当模型阶数N=10 时,式(8)~(10)中分别包含110、110、 90 个未知参数. 为求解未知参数,已知应力分量数量应大于未知参数的数量. 本文从 σx、 σy和τxy场分别均匀选择了140、140、110 个节点优化获得应力函数中的未知参数. 图5 所示为重构的残余应力场,与图2 对比可以看出重构的残余应力场与目标残余应力场较为吻合. 重构的3 个应力分量场的平均绝对误差为10.3 MPa,与无损测量法测量精度保持一致.

图5 三点弯重构残余应力场Fig.5 Reconstruction of residual stress field of three-point bending
2.2 铝合金板真实残余应力场重构
本小节将第1 节所提出的应力函数法应用于真实铝合金板的表面残余应力场重构,边长为70 mm的铝合金方板如图6 所示. 在铝合金板表面均匀选取64 个测点,即图6 中网格线的交汇处. 铝合金板在500 °C 高温下固溶2 h,通过X射线衍射法测量其表面各测点的残余应力 σx和 σy. 对于该铝合金板,使用所有测点数据进行重构来确定模型阶数,图7 所示为铝合金板判定系数与模型阶数的关系. 可以看出当N≥7 时,判定系数R2≥0.95,且判定系数随着模型阶数增大而趋于平缓,因此该铝合金板的模型阶数选为7. 式(8)~(9)包含未知参数数目分别为56和56 个,为了确定未知参数,64 个测点的残余应力分量全部用于铝合金的残余应力重构. 图8 为重构获得的铝合金板全场残余应力 σx和 σy,可以看出重构残余应力均为压应力. 为了与实测结果进行比较,图9 展示了铝合金板8 条水平线上 σx、 σy,可以看出各测点应力均为压应力,重构残余应力光滑地拟合了实测点残余应力.

图6 铝合金板及残余应力测点位置Fig.6 Aluminum alloy plate and locations of residual stress measuring points
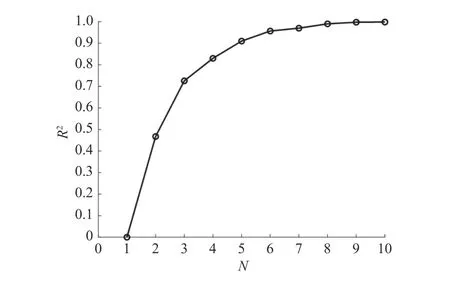
图7 铝合金板判定系数与模型阶数的关系Fig.7 Relationship between determination coefficient and model order of aluminum alloy plate

图8 铝合金板重构残余应力场Fig.8 Reconstructed residual stress field of aluminum alloy plate

图9 重构残余应力与实测残余应力比较Fig.9 Comparison between reconstructed and measured residual stresses
3 结 论
为改进应力函数法重构残余应力场时基函数难以选取的问题,本文使用双元傅里叶函数作为应力函数来逼近任意残余应力场分布,通过优化算法确定应力函数中的未知参数,实现了复杂残余应力场的重构,通过三点弯模拟残余应力场验证了该方法的准确性和可行性,并将其应用于真实铝合金板残余应力场重构,主要结论如下:
①使用傅里叶级数展开式作为艾瑞应力函数具有通用性,可表达复杂的残余应力分布. 在三点弯模拟实验中,本文同时重构3 个残余应力分量,重构场具有较高的精度.
②需要重构的测点个数可通过计算模型阶数确定,而模型阶数与判定系数R2呈正相关关系,可通过判定系数R2确定,避免了选择测点数目的盲目性.
③所提出的应力函数法应用于真实铝合金板残余应力重构具有较高的精度,85%以上测点处重构的残余应力相对误差在10%以内.

