基于贪婪量测划分的隐身目标跟踪MS-LMB 滤波器

孙进平，代贝宁，张玉涛

（1. 北京航空航天大学 电子信息工程学院，北京 100191；2. 中国船舶集团有限公司 第八研究院，江苏，南京 211153）

随着飞行器隐身技术的不断发展，对隐身目标的检测概率较低而使得雷达系统难以准确估计监测区域内目标状态的问题日益突出[1−2]. 雷达组网技术作为一种有效的反隐身措施，受到越来越多的关注与研究[3−4]. 多传感器多目标跟踪技术是雷达组网系统的核心技术之一，其本质即为根据多个传感器获得的目标信息来估计目标的状态，包括目标的起始，消亡，衍生，机动以及监测区域内的目标个数等[5].

传统的多目标跟踪是将量测同目标相关联，将多目标跟踪问题分解成单目标跟踪问题，但当观测场景中的目标数目较多或杂波较多时，数据关联算法极易出现组合爆炸的问题，会消耗大量的计算资源. Mahler 在多目标跟踪理论的基础上引入了随机有限集(RFS)理论，有效解决了传统算法会出现的组合爆炸问题[5]. 该类方法将多目标状态和多目标观测建模为RFS，通过贝叶斯滤波框架对多目标运动状态的后验密度进行近似估计. 其中概率假设密度(PHD)滤波器[6]、势概率假设密度(CPHD)滤波器[7]、多目标多伯努利(MeMBer)滤波器[8]、广义标签多伯努利(GLMB)滤波器[9]和标签多伯努利(LMB)滤波器[10]已成功应用于许多跟踪场景[11].

随着目标及实际监测场景的日益复杂，使得单部雷达的观测数据已经不能满足日益提高的目标跟踪要求，需要采用多雷达获取目标的信息. 为此，国内外众多学者将单传感器的RFS 滤波器推广到多传感器场景. 目前典型的多传感器RFS 跟踪方法有迭代校正式概率假设密度(IC-PHD)滤波器[12]，多传感器CPHD(MS-CPHD)滤波器[13]，多传感器多目标多伯努利(MS-MeMBer)滤波器[14]，多传感器广义标签多伯努(MS-GLMB)滤波器[15]和多传感器标签多伯努利(MS-LMB)滤波器[16]. IC-PHD 滤波器以迭代的方式依次对每个传感器上的量测数据进行单传感器PHD 滤波，该方法易于实现，但滤波性能会受到传感器顺序的影响. MS-CPHD 滤波器是一种多传感器近似滤波器，在更新过程中由于需要所有的量测划分结果而难以得到精确解，于是NANNURU[13]提出了一种两步贪婪划分机制，只求得有限个权重较高的量测划分假设，并通过高斯混合模型得到了其近似解. 之后，SAUCAN[14]提出一种精确的MS-MeMBer滤波器，并利用两步贪婪划分机制得到其近似解. 与MS-CPHD 滤波器相比，MS-MeMBer 滤波器直接用多伯努利分布来近似多目标后验密度，具有更高的滤波精度. 上述滤波器并未提供目标航迹，需要额外的航迹维持处理，文献[15]提出的MS-GLMB 滤波器使用标签RFS，并采用吉布斯采样得到量测划分结果，可高效输出目标的连续航迹，提高了实用性.VO 等[10]给出了LMB 滤波来近似GLMB 滤波，显著减小了计算量，且已推广至多传感器形式[16].

目前MS-GLMB 滤波器和MS-LMB 滤波器一般均采用吉布斯采样[15](GSM)来解决量测划分问题，本文将采用吉布斯采样的MS-LMB 滤波器记作MSLMB-GSM 滤波器. 在隐身目标的跟踪中，由于雷达对目标的检测概率比较低，若仍采用吉布斯采样，当雷达网中的多数雷达由于检测概率很低而都处于漏检状态时，量测分配的似然权值计算会受到影响，继而目标的状态估计和监视区域内目标数估计会出现错误. 为解决这一问题，本文采用贪婪量测划分(GPM)来解决MS-LMB 滤波器中的量测划分问题，将采用贪婪量测划分的MS-LMB 滤波器记作MSLMB-GPM 滤波器. 贪婪量测划分在按传感器顺序求取每一个目标的最优量测集时，由于保留了包含漏检项的量测集，因此可在多数雷达处于漏检状态时也能得到符合实际的量测划分结果，继而得到正确的多目标状态估计结果. 仿真实验表明，在隐身目标的跟踪中，MS-LMB-GPM 滤波器的滤波性能明显优于MS-LMB-GSM 滤波器.

1 LMB 随机有限集

本文分别采用如下函数表示集合中的广义 δ函数及包含函数[5]

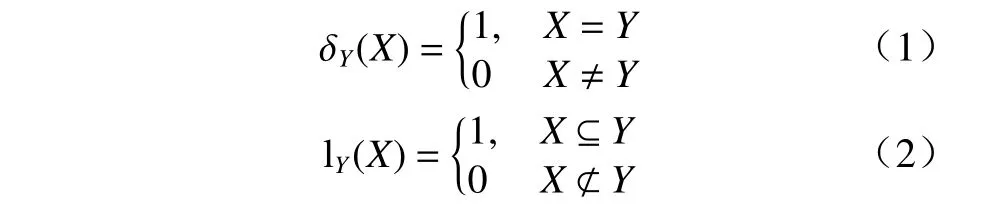
多目标状态采用标签随机集X表示，定义X={x1,···,xi,···,x|X|}，xi=(xi,ℓi)为 标签单目标状态， |X|表示集合X的势.

若X服从标签多伯努利分布，则密度函数可表示为[10]

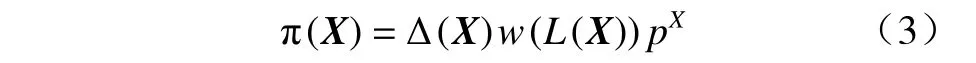
其中 ∆(X)=δ|X|[|L(X)|]为离散标签指示函数，可保证目标的状态集合和标签集合具有相同的势， L(−)表示目标的状态空间到标签空间的映射，具体形式为L(X)={L(x):x∈X}；pX=∏x∈X p(x,ℓ)为 集积分，p(x,ℓ)为目标x的概率密度函数. 权值函数w(L(X))可表示为

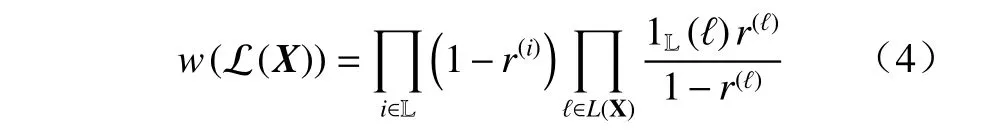
其中r(ℓ)表 示标签为 ℓ的目标存在的概率.

为方便表述，本文采用标签多伯努利分布密度函数的等效参数形式[10]，即为

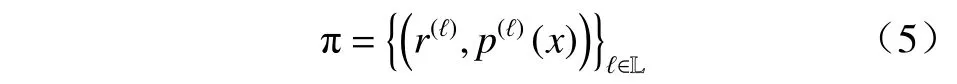
标签多伯努利分布的扩展形式为广义标签多伯努利分布，它的密度函数可表示为

其中 C是一个离散的索引集，权重w(c)(L(X))及概率分布p[(])满足归一化条件

2 MS-LMB-GPM 滤波器

2.1 预测过程

MS-LMB-GPM 滤波器的预测过程与单传感器LMB 滤波器的预测过程相同. 假设k−1时刻的标签多伯努利后验密度为

若k时刻的新生目标满足标签多伯努利分布，则可表示为

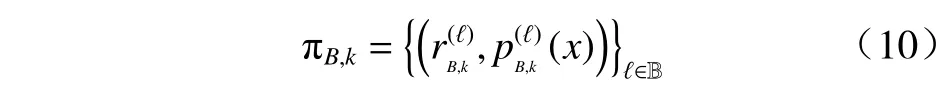
则预测概率密度仍为标签多伯努利形式，即有

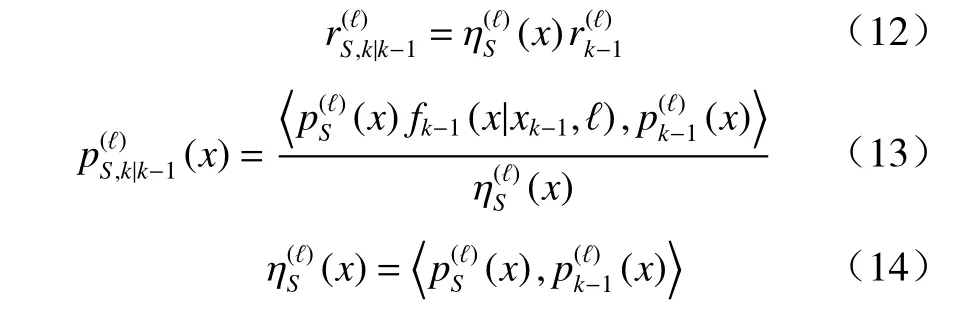
式中：fk−1(·|x,ℓ)表 示目标状态转移函数；(·)为目标的存活概率.

预测密度函数仍为标签多伯努利形式[14]，表示为

其中总标签集 L+=L∪B， 权重wk|k−1L(Xk|k−1)和概率密度函数pk|k−1(x,ℓ)分别为

2.2 贪婪量测划分

假设在k时刻，有M个 标签多伯努利项，并且S部雷达产生的量测集为={}，若雷达s有v个量测，则={} ， 其中表示雷达处于漏检状态. 将标签多伯努利项与量测划分结果的映射关系记为

其中 θ(m,s)代 表雷达s划 分给第m个标签多伯努利项的量测在雷达s所 有量测中的索引.

求出所有的量测划分假设的计算量很大，因此可求取有限个权重较高的量测划分假设作为量测划分结果，从而得到MS-LMB 滤波器的近似解.

文献[11,15]中均采用吉布斯采样来得到权重较大的量测划分假设. 假设有3 个标签伯努利项，3 部雷达(为方便展示，每部雷达仅画出3 个量测)，吉布斯采样的主要过程如图1 所示. 其中竖置立方体内为雷达3 所有量测，横置立方体内为求取第2 个标签伯努利项量测划分结果的主要过程. 吉布斯采样首先需要根据所有雷达量测的代价函数和分类分布判断该目标是否漏检，若为漏检则不再进行量测划分，否则再按照雷达顺序，根据代价函数和分类分布依次将各雷达量测划分给不同的标签伯努利项，且同一个量测最多只能划分给一个标签伯努利项.

图1 吉布斯采样Fig.1 Gibbs sampling method

在隐身目标跟踪中，雷达对目标的检测概率很低，容易处于漏检状态，导致计算出的似然权值偏小，因此采用吉布斯采样很难准确获取目标的量测. 并且在多目标跟踪中，若其中一个隐身目标只能被较少雷达探测到，则该目标相对于其他目标来说计算得到的似然权值更小. 导致难以对该隐身目标进行跟踪. 为解决此类问题，本文采用贪婪量测划分的方法解决MS-LMB 滤波器中的量测划分问题. 并且为保证多部雷达在处于漏检状态时也能得到正确的量测划分结果，在依次求取每个目标权重最大的几个量测集时，保留包含漏检项的量测集.

图2 和图3 为贪婪量测划分方法的具体过程. 假设接收到4 部雷达的量测数据，并且共有4 个预测的标签伯努利项. 第一步划分需要对每个标签伯努利项分别求其局部最优解，也就是求得部分权重较大的量测集. 求解过程按照雷达顺序依次进行，如图2所示，进行至最后一部雷达时，根据上一部雷达的量测划分子集分别求取所有可能的量测划分子集的权重，然后选取Wmax个权重较大的量测集作为该标签伯努利项的量测划分子集. 为保证在多部雷达处于漏检状态下，也可得到符合实际的量测划分结果，在按雷达顺序依次求取权重较大的Wmax量测集时，要额外保留包含漏检项的量测集. 将第m个标签伯努利项的Wmax个量测划分子集记作

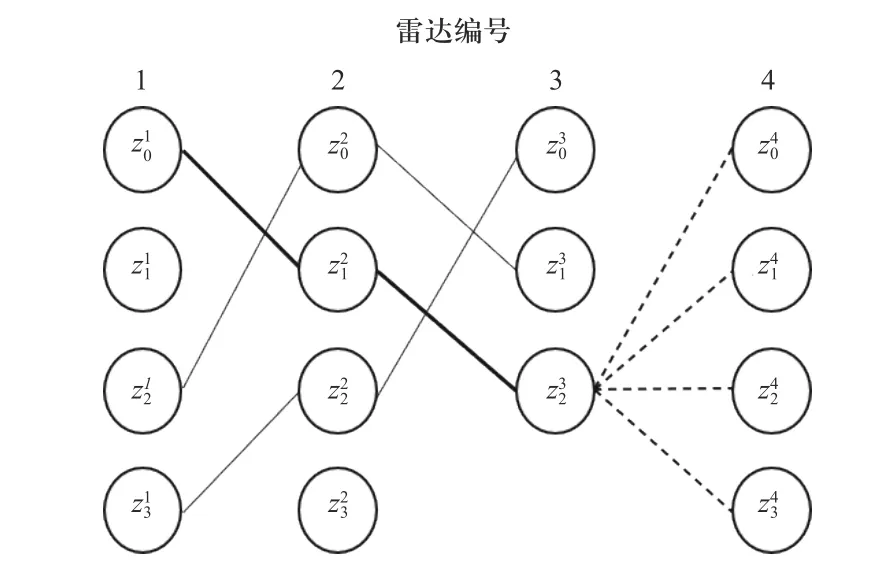
图2 第一步划分Fig.2 The first partitioning step

图3 为贪婪量测划分的第二步，将每个标签伯努利项的量测集组合成量测划分假设. 因为单个量测最多仅能划分给同一目标，因此在对不同的标签伯努利项的量测集进行组合时，要避免将一个量测重复划分给不同目标的情况. 为此需要把第一步得到的所有标签伯努利项的量测集中不相交的量测集挑选出来，将挑选后第m个标签伯努利项的量测集记作

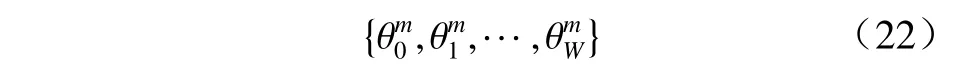
给定任意的量测划分假设θ，其权重计算式为

第二步划分的求解过程按照标签伯努利项的顺序依次进行. 如图3 所示，进行至最后一个标签伯努利项时，首先根据前一步(第3 个标签伯努利项)求取的Tmax个权重较大的量测划分假设分别计算下一步(第4 个标签伯努利项)所有量测划分假设的权重，然后取Tmax个权重较大的量测划分假设作为最终的量测划分结果.

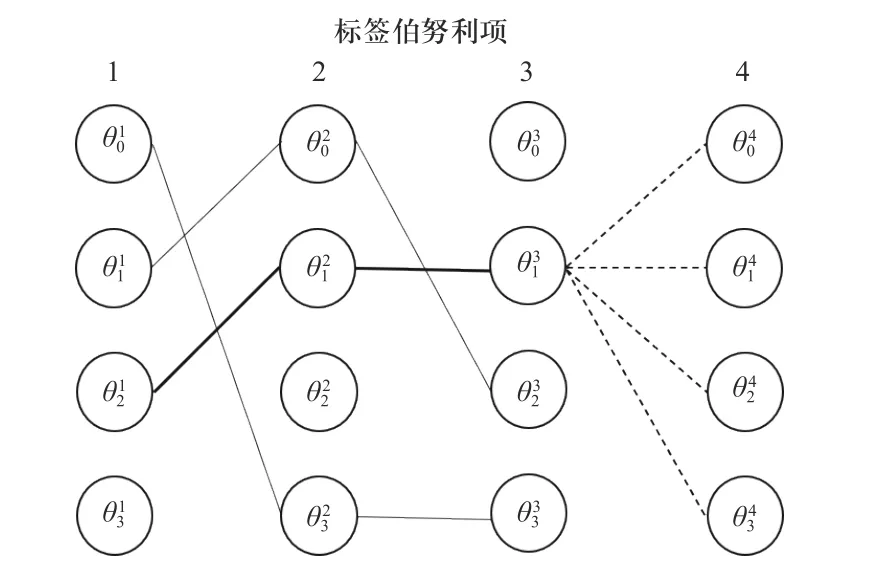
图3 第二步划分Fig.3 The second partitioning step

2.3 更新过程

预测后的多目标概率密度具有式(15)所示的形式，则采用量测划分的结果进行更新后的多目标概率密度函数服从GLMB 分布[12]，可表示为

其中F(L+)为 标签集 L+形 成的空间； ΘI+=为量测划分结果；I+={ℓ1,ℓ2···,ℓ|I+|}表示一种假设的标签集；权重(Z) 和 概率密度函数(x,ℓ)分别为

其中 〈·,·〉表示函数的内积.

为保证可进行连续更新，采用LMB 分布来近似GLMB 分布，则更新后的多目标后验密度可近似为

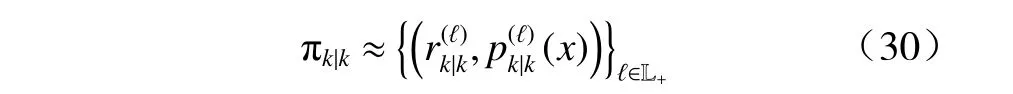
其中

2.4 高斯混合实现

在高斯混合模型下，目标的状态转移函数和量测似然函数均满足高斯分布

式中：Fk−1为 目标状态转移矩阵；Qk−1为过程噪声协方差矩阵；Hk为 单雷达的量测矩阵；Rk为单雷达的量测噪声协方差矩阵.

滤波处理时设各雷达检测概率为

假设k−1时刻每个标签多伯努利项概率密度具有如下高斯混合的形式

其中下标j是为了区分同一标签伯努利项中的不同高斯混合项.

存活目标的标签多伯努利项概率密度仍为高斯混合的形式

其中

假设新生目标的标签多伯努利项概率密度具有如下高斯混合的形式

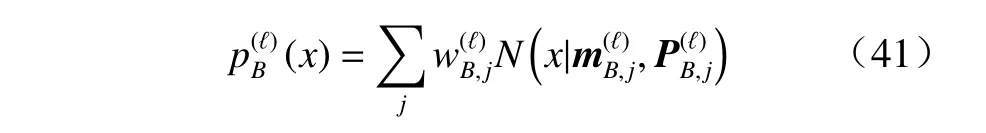
则经过预测，目标的预测标签多伯努利项概率密度即为如下高斯混合形式

根据预测结果进行量测划分，采用量测划分的结果进行更新，更新后多目标的标签多伯努利项概率密度即为如下高斯混合形式

各高斯混合分量的权重为

各高斯混合分量的均值和方差更新式分别为

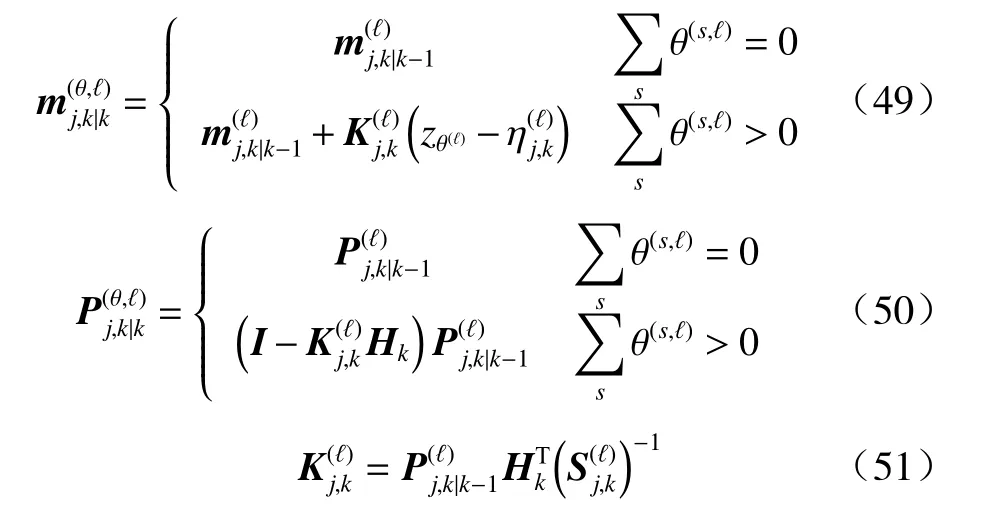
3 仿真实验与分析

3.1 隐身目标仿真

本文仿真场景中所采用的隐身目标RCS 曲线如图4 所示，该曲线来自参考文献[17]中对F-22 飞机缩比模型在微波暗室的实际测量结果.

图4 隐身目标RCS 曲线图Fig.4 RCS curve of stealthy target

雷达对目标检测概率的计算十分复杂，所涉及的因素众多，本文采用文献[18]中给出的计算检测概率的近似表达式

式中：Ar为雷达自身的性能参数，Ar=σr/， σr为参考RCS 值，Rr为 检测概率为0.5，给定目标RCS 为σr时雷达的最大探测距离；R为目标与雷达的距离；σ为目标的RCS.

3.2 算法仿真

仿真场景如图5 所示，主要研究二维观测区域下运动模型为CT 模型的隐身目标. 目标的状态变量为[]T,包括目标的位置，速度及转弯速率. 设 ω0=π/180(rad·s−1)，目标的具体运动情况如表1 所示.

图5 目标真实运动轨迹Fig.5 True movement trajectories of target

表1 目标真实运动情况Tab.1 True movement of targets

观测过程共持续100 帧，采样间隔为 ∆t=2 s. 观测共采用6 部雷达，性能参数均相同(目标RCS 为1 m2时，最大探测距离为Rr=400 km)，雷达的具体位置如表2 所示，杂波强度 λ=10. 量测仿真时各雷达的检测概率根据式(52)计算得到，滤波处理时各雷达检测概率为pD=0.8. 根据目标初始状态设置新生目标模型，目标存活概率为pS=0.99. 目标状态转移矩阵Fk、 过程噪声协方差矩阵Qk、 量测矩阵Hk、量测噪声协方差矩阵Rk分别为

表2 雷达位置Tab.2 Radar location

其中，过程噪声标准差 σv=1 km/s ，量测噪声标准差σε=10 m.

在仿真中，为了防止跟踪目标的标签伯努利项数目及高斯混合分量无限增长，设置跟踪目标的标签多伯努利项的上限为Mmax=100，高斯混合分量的上限为Jmax=100，高斯混合分量的剪枝门限及合并门限分别为Gc=10−2，Gm=1. 量测分割假设集 Θ中最多有8 个量测分割假设θ，每个标签伯努利项对应的量测集上限Wmax=8. 本节进行50 次蒙特卡罗实验取平均结果，且滤波性能使用式(57)所示的OSPA 距离作为衡量标准[5].

式中，阶数p=1， 截断门限c=100.

图6 即为所有雷达的量测点迹及MS-LMB-GPM滤波器与MS-LMB-GSM 滤波器的跟踪结果. 从图6(b)(c)可以看出，MS-LMB-GSM 滤波器在雷达性能较差(Rr=400 km)时无法稳定跟踪目标3 和4，而MSLMB-GPM 滤波器在同等雷达性能下能够对所有隐身目标进行稳定跟踪，并输出所有目标的航迹. 从图6(d)可以看出，MS-LMB-GSM 滤波器在雷达性能提升至Rr=550 km时才能实现对所有隐身目标的稳定跟踪.

图6 量测及跟踪结果图Fig.6 Measurements and tracking results

图7 为仿真过程中所有雷达对目标2，4 的检测概率随时间的变化曲线. 以目标2，4 为例分析目标的检测概率对跟踪效果的影响. 通过图7(a)可看出目标2 在跟踪初始阶段，雷达2 和3 的检测概率较高（接近于1）；雷达1、4、5 和6 检测概率略小，但均大于0.6；除雷达6 外其余雷达的检测概率在仿真过程中均较高. 而通过图7(b)可以看出目标4 在刚出现时，雷达3 和5 的检测概率较高；雷达2 和雷达6 的检测概率略低，在0.6 左右；雷达1 和4 的检测概率较低，在0.5 左右，且雷达1 的检测概率呈剧烈减小趋势，因此雷达1 和4 在目标刚出现时很大概率都处于漏检状态；并且雷达1、2、4 和6 的检测概率在整个仿真过程中波动幅度很大. 因此若采用吉布斯采样进行量测划分，目标4 相对于目标2 处于漏检状态的雷达数目更多，目标4 更容易被跟丢. 若采用贪婪量测划分，该问题得以解决. 由于单独考虑了包含漏检项的量测集，因此贪婪量测划分方法可在较多雷达处于漏检状态的情况下也能得到符合实际的量测划分结果，因此对目标2，4 均能进行稳定跟踪.

图7 检测概率曲线图Fig.7 Curve of Pd

图8 为MS-LMB-GPM 滤波器与MS-LMB-GSM滤波器分别进行50 次蒙特卡罗实验的势估计均值和标准差. 通过对比势估计结果可以看出，MS-LMBGSM 滤波器在雷达性能较差(Rr=400 km)时出现了严重的势估计偏差，而MS-LMB-GPM 滤波器在同等雷达性能下能得到较为准确的势估计结果，与MSLMB-GSM 滤波器在雷达性能提升至Rr=550 km的势估计结果十分接近. 图9 为MS-LMB-GPM 滤波器与MS-LMB-GSM 滤波器分别进行50 次蒙特卡罗实验的OSPA 距离结果对比. 可以看出MS-LMB-GSM滤波器在雷达性能较差(Rr=400 km)时的滤波性能较差，由于容易跟丢目标3 和4 而导致OSPA 距离明显较大；而MS-LMB-GPM 滤波器在同等雷达性能下的OSPA 距离明显较小，且与MS-LMB-GPM 滤波器在雷达性能提升至Rr=550 km时的OSPA 距离十分接近. 因此，相较于MS-LMB-GSM 滤波器，MS-LMBGPM 滤波器在同等雷达性能的情况下具有更优的隐身目标跟踪性能.

图8 势估计结果Fig.8 Estimated cardinality

图9 OSPA 距离Fig.9 OSPA distance

在 AMD Ryzen 7 4800H 处 理 器、R2020a 版 本MATLAB 软件平台下，MS-LMB-GSM 滤波器和MSLMB-GPM 滤波器在雷达性能相同(Rr=400 km)时进行50 次蒙特卡罗实验的平均单次运行时间如表3所示，可以看出MS-LMB-GPM 滤波器在同等计算复杂度下提升了跟踪隐身目标时的滤波性能.

表3 OSPA 及运行时间对比Tab.3 Comparison of OSPA and running time

4 结 论

目前MS-LMB 滤波器多采用吉布斯采样来解决量测划分问题. 但是在隐身目标的跟踪中，雷达会因为检测概率很低而处于漏检状态. 当多数雷达都处于漏检状态时，隐身目标的似然权值偏小，使得吉布斯采样很难采样到目标量测，从而难以对该隐身目标进行稳定跟踪. 为解决这一问题，本文采用贪婪量测划分的方法来解决量测划分问题. 该方法在得到每个目标的量测集时专门保留包含漏检项的量测集，保证了符合实际的量测划分结果不会因似然权值偏小而难以得到. 仿真结果表明，在雷达性能相同时，MS-LMB-GPM 滤波器具有明显优于MS-LMB-GSM滤波器的多雷达隐身目标跟踪效果.