基于改进广义线性组合算法的极化阵列稳健波束形成

吕岩，曹菲，杨剑，冯晓伟，何川

（1. 火箭军工程大学 核工程学院，陕西，西安 710025；2. 中国人民解放军 96746 部队，新疆，库尔勒 841000；3. 火箭军工程大学 导弹工程学院，陕西，西安 710025）

阵列信号处理作为一种空间滤波技术，可通过调整阵元权值控制波束形成，使其在期望信号(signal of interest, SOI)方向形成高增益波束，同时抑制干扰信号方向的增益. 目前，波束形成算法已被广泛应用于雷达、声呐、地震波监测、通讯和医学等领域[1−3]. 极化阵列[4]不同于传统相控阵，能够获取空间电磁波的极化方式信息，从而将信号极化域和空域信息相结合，可有效克服空域滤波的不足[5−6].

自适应波束形成算法在信号模型出现阵元位置扰动和波达方向(direction of arrival, DOA)误差时，性能将会严重下降. 为了提升波束形成的稳健性，对角加载技术被广泛应用于阵列信号处理中. 广义线性组合(general linear combination, GLC)算法[7]是一种在最小均方误差(minimum mean square error, MMSE)准则下估计阵列理论协方差矩阵的算法，能够依据采样协方差矩阵(sample covariance matrix, SCM)自动确定对角加载量(diagonal loading level, DLL)，从而提升有限快拍条件下阵列波束形成的稳健性. WANG等[8]中提出了一种使用两种收缩方案的改进GLC算法，分别使用原GLC 算法和经指数矩阵改进的GLC 算法确定DLL，获得了更高的输出信干噪比.KE 等[9]首先研究了不同算法在快拍数和传感器数量较大时的性能，并针对GLC 算法的不足，提出了结合数据降噪预处理和MMSE 准则估计真实协方差矩阵的自动确定DLL 算法，该算法在高快拍和多传感器条件下性能优于其他算法，但在快拍数较低时，过大的DLL 将会影响阵列输出的信干噪比.GAN 等[10]基于高斯分布提出了一种改进的GLC 算法，该算法在保持GLC 算法性能的同时具有更低的计算复杂度. YUAN[11]通过添加协方差矩阵相关的系数对GLC 算法收缩矩阵进行改进，得到了比GLC算法更大的DLL，但该算法在输入信噪比较高时性能受限.

为了提升极化敏感阵列波束形成的稳健性，本文将GLC 算法应用于极化敏感阵列. 分析了信噪比较高时，GLC 算法在阵元扰动和SOI 存在DOA 误差情况下的输出信干噪比随快拍数增加而下降的原因，并提出了一种结合转换函数的改进GLC 算法. 所提算法依据SCM 特征值相关参数的大小，对信噪比进行判断. 信噪比较高时，采用改进GLC 算法计算DLL；信噪比较低时，采用原GLC 算法计算DLL. 最后，通过主瓣干扰条件下的仿真实验验证了所提算法的性能.

1 信号模型

如图1 所示，考虑一个由N组正交偶极子对组成的均匀线阵，阵元间距为入射信号半波长d=λ/2，每组正交偶极子分别沿X轴和Y轴放置.

图1 极化阵列结构Fig.1 Structure of polarization array

假设远场空间中存在1 个SOI 分量s0(t)和J个互不相关的干扰信号s1(t),s2(t),···,sJ(t)（均为窄带信号），其中SOI 的DOA 为 [θ0,φ0]， 干扰信号DOA 为[θ1,φ1],[θ2,φ2],···,[θJ,φJ]， 则 阵 列 在 瞬 时 时 刻t接 收 到 的 信号为

式中：ai=⊗为极化-空域联合导向矢量；n(t)为加性高斯复噪声； ⊗表示Kronecker 乘积运算；表示极化导向矢量分量[12]：

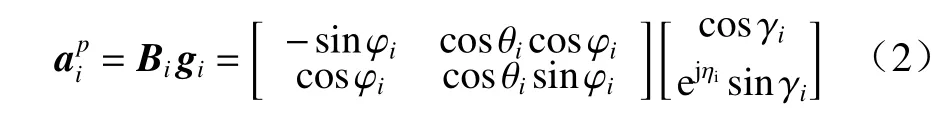
式中：Bi表示入射信号在各电偶极子上的投影矩阵；gi为 入 射 信 号 的 极 化 信 息； γi和 ηi代 表 极 化 参 数，tanγi=AY/AX表示电场极化幅度比，满足 γi∈[0,π/2]，ηi=ϕY−ϕX为电场极化相位差， ηi∈[0,2π]. 为便于分析，假设入射信号位于XOY平面内，则可得

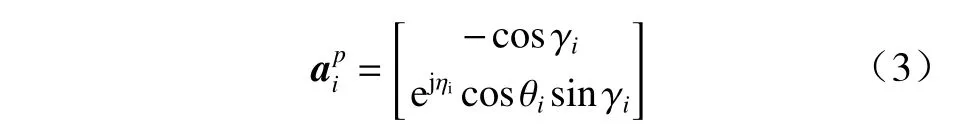
则阵列接收数据X(t)的协方差矩阵为[13]

式中：E(·)表 示期望运算； (·)H代 表Hermitian 转置运算；表示入射信号功率；为 噪声功率，I代表单位矩阵；Ri+n为理想的干扰加噪声协方差矩阵. 基于Capon 波束形成器(standard Capon beamformer, SCB)，阵列的最优权值矢量和最优输出信干噪比可表示为

2 GLC 算法及改进

2.1 极化阵列GLC 算法

对角加载技术[14−15]可以使SCM 的小特征值散布程度变低，从而提升波束形成的稳健性，尤其在快拍数较低的情况下，对角加载算法对方向图的稳定性和输出信干噪比的提升效果较为显著，但最优DLL 的选取相对困难. GLC 算法可根据SCM 参数自动确定DLL，描述如下：

在GLC 算法中，RX被估计为

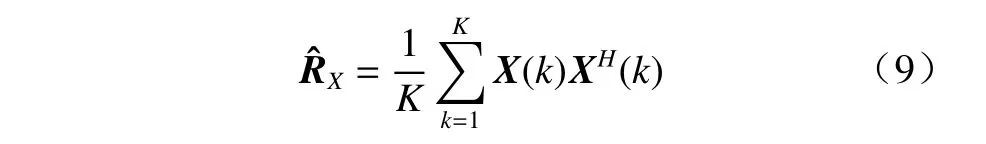
其中，K为快拍数. 式(8)中， α 和 β可通过MMSE 方法获得

经过推导，可得

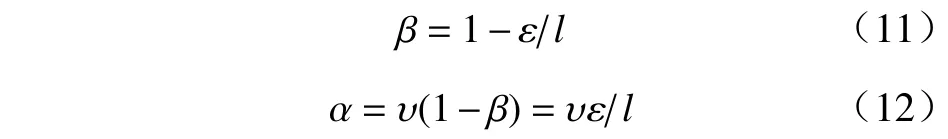
其中:

其中， tr(·)表示矩阵求迹运算. 经过GLC 算法计算极化阵列模型的DLL，可得阵列的权值矢量.

此时，波束形成器输出的信干噪比为

2.2 GLC 算法的不足

根据文献[7]可知，随着快拍数的增加，由GLC算法所得的DLL 逐渐降低并趋近于0，此时将逐渐接近于理论协方差矩阵RX，为便于理论推导，使用RX代 替SCM 进行后续分析. 若SOI 的导向矢量a0不存在误差，则阵列输出的信干噪比为

在实际应用中，由于存在SOI 的DOA 误差或者阵元位置扰动，a0无法准确获取. 假设估计的SOI 导向 矢 量 为ad，和a0之 间 满 足：ad=a0+ae， 其 中ae表 示两者之间的误差. 将ad和RX代入式(16)求出权值矢量，并代入式(17)计算阵列输出为

利用矩阵求逆公式，根据式(5)可得

将式(20)代入式(18)和式(19)，并计算两者之间的差值：

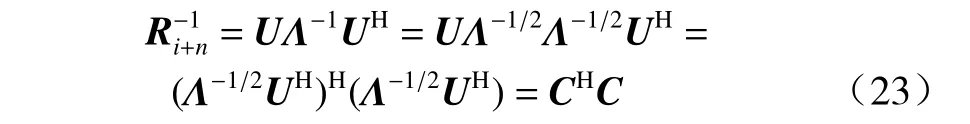
式中： Λ为对角矩阵，对角线元素表示Ri+n的特征值；U为对应的特征向量所组成的矩阵. 将式(23)代入Θ可得

将式(24)中Cad记 为c1，Ca0记 为c2，可得：

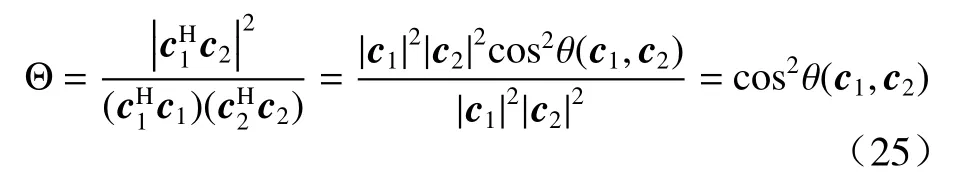
由式(25)可知 Θ ≤1， 代入式(22)，可得 S INRdif>0，且SCM 中所含的SOI 功率越大或者ae越 大，则SINRdif也随之增大. 可得结论：当信噪比较高时，若阵列模型存在DOA 误差或阵元位置扰动误差，此时随着快拍数的增加，由GLC 算法所得的阵列输出要远低于不存在误差时的输出 SINRpol.

2.3 改进GLC 算法

由2.2 节可知，快拍数较高时，若阵列模型出现误差将导致GLC 算法性能下降，因此需要在原GLC算法的基础上，提升其在高快拍时的DLL. 根据式(11)和式(12)，可得

本文采取放大式(14)中的参数 ε提升DLL，为使调整后的DLL 与快拍数相关，在 ε基础上乘以一个系数项，构造ˆε

其中k为当前阵列接收的快拍数， ρ ∈[0,1]表示阶次，易知 εˆ>ε. 从式(27)可以看出，使用 εˆ 代 替 ε能够达到提升DLL 的目的. 根据文献[9]，当快拍数较低时，DLL 过大会使阵列输出信干噪比降低，因此所提算法需要在低快拍时保持原GLC 算法的性能，快拍数较高时能够随之增大DLL. 基于以上分析，构造转换函数为

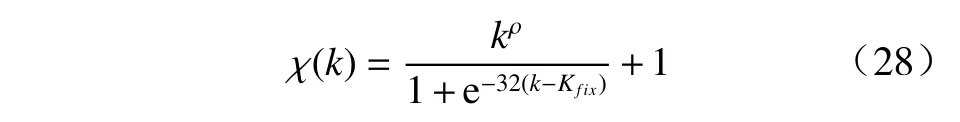
其中，Kfix∈[1,K]为设定的快拍转换参数. 由式(28)可知，当k≤Kfix时 ， χ(k)≈1； 当k>Kfix时 ， χ(k)≈kρ+1.假设k∈[0,500]，Kfix=200， ρ分别为1/3、1/2、2/3 的曲线如图2 所示.

图2 转换函数曲线Fig.2 Curve of transformation function

将原GLC 算法中式(14)修改为

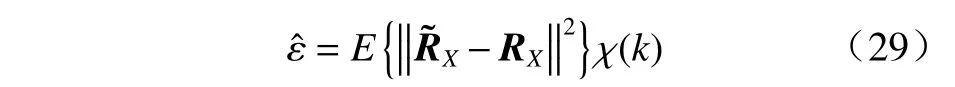
根据式(29)可知，当k≤Kfix时 ， χ(k)≈1，与原GLC算法一致；当k>Kfix时 ， εˆ 被 放大 χ(k)倍，致使DLL 较原GLC 算法有所提升.

式中： δn为 降序排列的特征值；un代表与之对应的特征向量；D表示入射信号数量，前D个特征值属于信号加干扰子空间，其余 2N−D个较小特征值构成噪声子空间. 阵列入射信号的个数可使用信源数量估计算法获得[16]，所以类似于文献[17]，本文假设D已知.干扰信号功率一般远大于SOI 和噪声功率，因此能够通过特征值 δD的幅度判断信噪比的高低程度. 根据文献[18]的判定方法，当输入信噪比较高时，所有较小特征值的和小于最小信号子空间特征值和最大噪声子空间特征值的差值，即

定义不等式(31)中的参数：

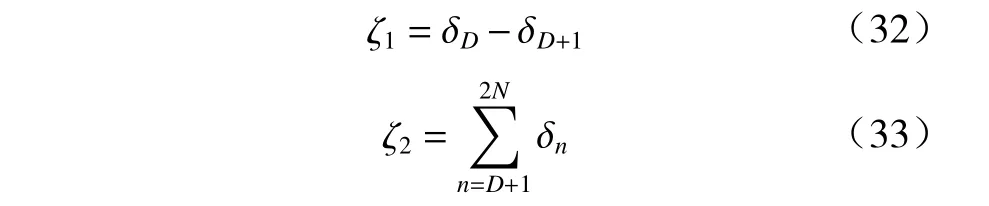
当 ζ1>ζ2时，判定为信噪比较高，此时需采用结合转换函数的GLC 算法计算DLL；反之当 ζ1＜ζ2时，则采用原GLC 算法计算DLL.

2.4 算法步骤

根据以上分析，总结所提算法步骤如下.

②根据式(32)和式(33)计算参数 ζ1与 ζ2， 若ζ1＜ζ2，则执行步骤(4)，否则执行步骤(3)；

④根据式(13)、(14)和(15)计算 υ、 ε和l，确 定DLL，转步骤(5)；

⑤根据式(16)计算阵元权值矢量，算法结束.

3 仿真分析

仿真基于极化敏感均匀线性阵列，正交偶极子对数量N=10，入射信号频率设置为2.2 GHz，阵元间距为入射信号半波长. 入射信号的极化参数设置为：γ0=γ2=45◦、γ1=30◦、η0=180◦、 η1=150◦、 η2=70◦.空 域参 数设置为：SOI 的DOA 为 θ0=25◦、干扰信号DOA 为 θ1=−15◦和 θ2=22◦. 当存在阵元位置扰动误差时，设定其随机分布在[(n−1)d−0.05λ,(n−1)d+0.05λ]范围内；SOI 存在DOA 误差时，设置其随机分布在[θ0−2◦,θ0+2◦]范 围内，其中 θ0代表真实DOA. 仿真中信噪比设置为较高值等于10 dB（3.4 节除外）、干噪比设置为20 dB、快拍数量取10～500 拍，仿真中所得的结果均为200 次蒙特卡罗实验后的平均值.

3.1 算法参数选取

根据式(28)可知，所提算法需要确定的参数分别为阶次 ρ和快拍转换参数Kfix. 假设阵元位置扰动和SOI 的DOA 误差同时存在，选取 ρ分别等于0、1/6、2/6、3/6、4/6、5/6 和1 绘制阵列输出信干噪比随快拍数变化的曲线如图3 所示. 在构造转换函数过程中，为保证低快拍时 χ(k)≈1， 需向系数项kρ中添加常数1，图3 一并对比了采用式(27)和式(34)对阵列输出信干噪比的影响，其中式(34)为

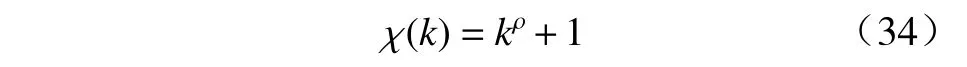
从图3 可以看出，阶次较低时，由式(27)和式(34)所得的输出信干噪比随快拍数的升高出现较大差异，且呈现出逐渐下降的趋势，表明DLL 不足. 当阶次设置为 ρ=1/2时，高快拍条件下阵列输出的信干噪比要比其他阶次更优，并且此时采用式(27)和式(34)计算DLL 所得的输出信干噪比曲线基本一致，因此设置阶次 ρ=1/2. 为使所提算法在低快拍时保持原GLC 算法性能，高快拍时能够利用转换函数提高DLL，选择 ρ=1/2与原GLC 算法的曲线交点作为快拍转换参数，设置Kfix=70.

图3 不同阶次输出信干噪比的变化趋势Fig.3 Trends in output signal to interference plus noise ratio of different orders

3.2 阵元扰动对阵列输出信干噪比的影响

为验证所提算法性能，将其与SCB、HKB[7](Hoerl-Kennard-Baldwin)、原GLC 算法和GLC 的一种改进算法LS-TMMSE[9]相对比. 图4 和图5 分别为不同算法输出信干噪比和DLL 随快拍数的变化趋势.

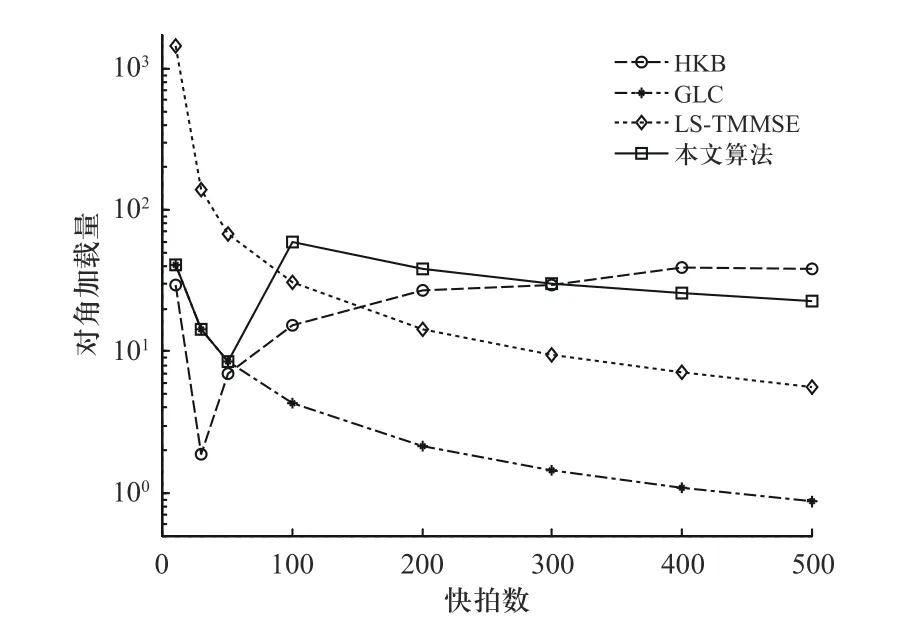
图5 对角加载量对比Fig.5 Comparison of average diagonal loading levels

根据图4 可知，由于主瓣内部存在一个干扰信号，导致最优信干噪比较非主瓣干扰有所降低，但因该干扰和SOI 的极化参数存在一定差异，使得最优信干噪比仍能够达到较高水平. 其中，非主瓣干扰条件下阵列输出的最优信干噪比为[19]

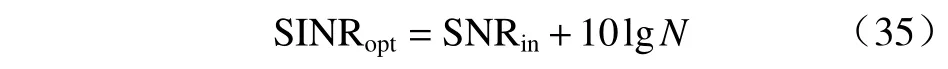
图4 不用算法输出信干噪比的变化趋势Fig.4 Trends in output signal to interference plus noise ratio of different algorithms

其 中 SNRin表 示SOI 的 功 率， lg(·)为 取 以10 为 底 的 对数运算. 从图4 还可以看出，对角加载类算法输出的信干噪比均大于SCB. 当快拍数较低时，由于所提算法的转换函数值约等于1，所以该算法性能和原GLC 算法保持一致；随着快拍数的升高，GLC 算法性能严重下降，输出信干噪比均低于其他算法；与之相异，由于所提算法利用转换函数有效提高了DLL，在快拍数较高时输出信干噪比达到了最高，并且变化趋势较为稳定. 从图5 可知，LS-TMMSE 算法由于在低快拍时采用较大的DLL，所以其性能不及GLC算法. GLC 算法随快拍数升高DLL 逐渐趋于0，而所提算法在快拍数较高时的DLL 大于GLC 算法，因此使阵列具备更好的稳健性能.

3.3 阵元扰动加DOA 误差对阵列输出信干噪比的影响

图6 和图7 分别为不同算法输出信干噪比与DLL 随快拍数量的变化情况. 对比图4 和图6 可以看出，在阵元扰动加DOA 失配的复杂条件下，所有算法输出的信干噪比均有所降低，但所提算法在快拍数较高时仍优于其他算法. 对比图5 和图7 可以发现，在快拍数较高时GLC 算法的DLL 趋近于0，所以GLC 算法输出的信干噪比下降最为严重；相反，所提算法由于适度提高了DLL，从而使其输出的信干噪比高于GLC 算法.

图6 不同算法输出信干噪比的变化趋势Fig.6 Trends in output signal to interference plus noise ratio of different algorithms

图7 对角加载量对比Fig.7 Comparison of average diagonal loading levels

3.4 输入信噪比对阵列输出信干噪比的影响

主要检验主瓣干扰条件下，阵元扰动和阵元扰动加DOA 误差两种情况时，输入信噪比变化对阵列输出信干噪比的影响，快拍数设置为K=300. 图8 为阵列输出信干噪比随输入信噪比的变化曲线，可以看出所提算法的性能优于GLC 算法，尤其在信噪比较高时性能差异较为明显. 当信噪比较低时，LSTMMSE 算法输出的信干噪比较所提算法略高，随着信噪比的提升，所提算法超过了其余算法，使阵列获得了更优的输出.

图8 信干噪比随输入信噪比的变化曲线Fig.8 Signal to interference plus noise ratio of different algorithms versus input signal to noise ratio

4 结 论

①本文将GLC 算法应用于极化敏感阵列，根据SCM 特征值相关参数的大小判定信噪比，从而选择不同的DLL 计算策略；

②分析了信噪比较高时，GLC 算法性能下降的原因，提出了一种结合转换函数的改进GLC 算法，所提算法能够在低快拍时保持GLC 算法的性能优势，当快拍数较高时，通过增大DLL 进一步提升了极化阵列在复杂误差条件下波束形成的稳健性；

③通过阵元扰动和阵元扰动加DOA 误差主瓣干扰条件下的仿真实验，验证了所提算法在输入信噪比和快拍数较高时的性能均优于原GLC 算法和其他几种典型算法.