线性聚焦式杀伤战斗部设计及破片飞散特性
葛超,王晋,郑元枫,王海福,余庆波
(北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
聚焦式杀伤战斗部是爆炸能量高效分配利用的有效手段,其基本技术理念为通过内凹型装药曲线,控制破片飞散汇聚于狭窄、高密度的聚焦带内[1−5].同时聚焦战斗部破片–冲击波联合作用[6−8]对目标的毁伤能力比普通破片杀伤战斗部更突出.
国内外学者就聚焦式杀伤战斗部装药结构设计展开研究,获得了静爆条件下装药结构参数对破片聚焦性能影响规律[9−11],并给出聚焦式杀伤战斗部工程设计方法. 现有研究主要针对破片聚焦点展开,尤其关注静态条件下装药表面偏转角对破片飞散方向和聚焦带宽度变化的影响规律[12−15],但聚焦带破片速度分布差异及其对动态聚焦性能影响的相关研究还不深入. 传统聚焦式杀伤战斗部由于起爆位置不同、破片排布方式差异及爆轰稀疏波影响,装药起爆后,作用于预制破片的冲量不同,导致轴向破片间速度差异显著. 因此破片群在飞散方向存在显著速度梯度,导致破片不能同时击中目标. 动态弹目交汇条件下,由于破片达到目标的时间不同,着靶破片密度降低,显著影响破片动态聚焦性能及战斗部终点毁伤威力[16]. 降低速度梯度,可实现在高速弹目交汇条件下破片仍可同时击中目标,提高着靶破片分布密度,从而显著提升聚焦战斗部终点毁伤威力. 因此,优化战斗部结构、减小破片速度梯度,获得等速破片场成为聚焦战斗部工程设计关键技术问题.
工程上获得等速破片场的主要途径有曲线装药、波形控制器、装药内腔以及特定传爆序列等. 其中波形控制器和装药内腔由于低装填比,产生的破片速度较低,且特定传爆序列精度要求高,制作工艺复杂[17]. 曲线装药通过调控装药表面冲量获得等速破片,具有工艺简单、成本低廉等优点.
为获得等速破片场,结合破片线性聚焦式杀伤战斗部结构技术原理[18],本文分析了装药爆轰冲量场分布,建立了等冲量装药曲线模型,可使破片在飞散聚焦过程中形成低聚焦宽度、高破片密度的等速线性聚焦带,并基于Ls-Dyna 有限元分析平台对线性聚焦破片场形成过程展开数值模拟研究,得到装药结构参数对破片场速度分布梯度影响规律,为高性能聚焦战斗部设计提供了新的技术支撑.
1 线性聚焦式杀伤战斗部设计理论
1.1 破片线性聚焦原理
为实现聚焦战斗部破片着靶落点线性分布,可通过调整聚焦战斗部装药表面破片排布,调整破片飞散特性,使破片在聚焦带内呈线性排布即线性聚焦,线性聚焦破片落点分布[18]如图1 所示.
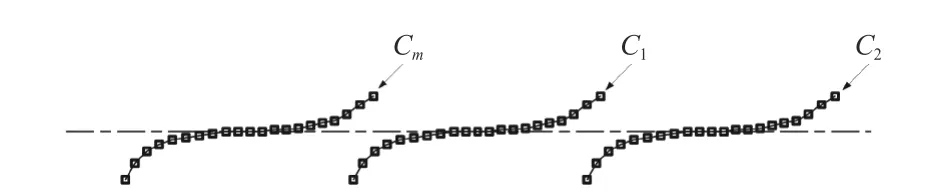
图1 线性聚焦杀伤战斗部破片落点Fig.1 Fall points of fragments from linear focusing warhead
利用依附于装药药柱表面的周向坐标和轴向坐标,描述破片位置,如图2 所示[18].L为装药长度;D为装药大端直径;破片质心所在曲线的切线与装药轴线夹角为θ;R为破片所在行;C为破片所在列;破片共排布n行、m列.

图2 破片排布周向坐标和轴向坐标Fig.2 Circumeferential and axial coordinates of fragments
装药药柱及起爆方式满足轴对称条件时,假设破片受爆炸驱动后沿直线飞行. 取第n行破片,靶板上落点的周向坐标与破片排布周向坐标一致,如图3所示[18]. 因此,可通过破片周向排布设计来控制破片落点相对位置. 取第m列破片,破片在目标靶板上落点位置和顺序与破片轴向排布位置和顺序一一对应,如图4 所示[18]. 基于上述破片直线飞行假设、破片排布方式和着靶落点关系,通过破片轴向和周向排布设计调控落点相对位置,即可实现聚焦战斗部爆炸驱动线性聚焦.

图3 破片周向排布与落点关系Fig.3 Relationship between circumrefential arrangement and fall point of fragments arrangement

图4 破片轴向排布与落点关系Fig.4 Relationship between axial and fall point of fragments
1.2 破片线性排布方法
基于破片线性聚焦原理,结合破片排布与落点匹配关系,紧密、均匀、周期性对破片进行排布. 聚焦战斗部破片共有m列,沿周向均匀分布,每列中有n个破片,列向破片质心连线与战斗部轴线夹角均为θ,以满足各列破片在周向上首尾相连. 将破片排布平铺至平面,周向坐标转化为横坐标,轴向坐标转化为纵坐标,平面坐标系下破片排布方法如图5 所示.
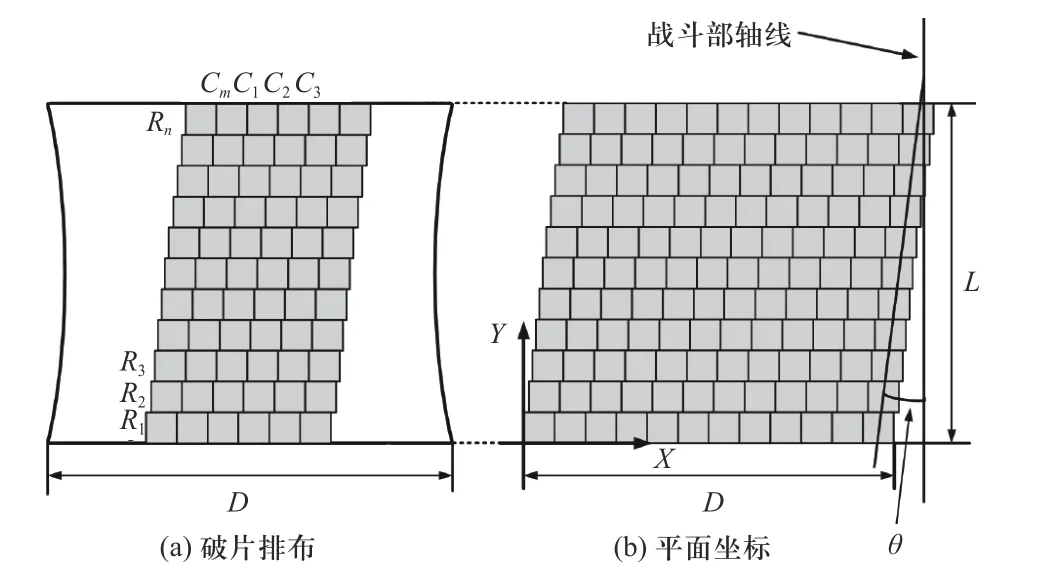
图5 平面坐标下破片排布方法Fig.5 Fragments arrangement method in plane coordinate system
为表征各列破片的位置关系,引入两个概念:重叠长度Δl和重叠度 γ. 平面坐标系内,一列破片所占周向长度为l,相邻两列破片周向重叠长度为Δl,重叠度 γ为重叠长度与单个破片所占周向长度的比值,如图6 所示. 重叠度是描述相邻两列破片位置关系的关键参数. 重叠长度和重叠度计算公式如下:
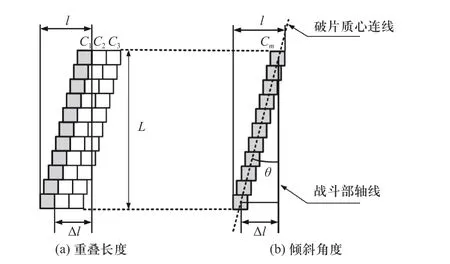
图6 破片重叠长度与倾斜角度示意图Fig.6 Overlap length and tilt angle of fragments

则列向破片质心连线与战斗部轴线夹角θ为[18]

式中:l为一列破片所占周向长度; γ为重叠度;m为破片列数;n为每列破片数;D为战斗部直径;L为战斗部长度.
2 等冲量聚焦曲线设计
2.1 爆炸冲量轴向分布
三维条件下,柱形装药爆炸后,产生的爆炸冲量沿装药轴线方向呈现复杂分布特性. 基于Станюкович理论[19−20],在战斗部轴线方向,破片速度与爆炸冲量的关系表述为

式中:vm为破片径向速度最大值;ix为装药轴向x位置处爆炸冲量;im为轴线上爆炸冲量最大值. 基于式(3),则可通过调整装药曲线形状,调控炸药轴向爆炸冲量并使其趋于一致,进而使破片径向飞散速度一致.
Баум-Станюкович公式[19−20]精确描述了两端开口侧向固壁、一端起爆时爆炸冲量沿轴向的分布,爆炸冲量与轴线上位置x的关系可表示为
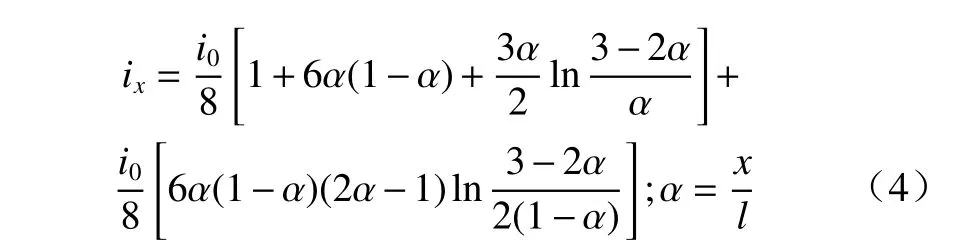
式中:i0为装药非起爆端面受爆轰波迎面作用比冲量,i0=ρ0lD, 其中 ρ0为装药密度,l为装药长度,D为炸药爆速; α为药柱上相对位置;x为药柱某处与起爆点的轴向距离. 式(4)揭示了爆炸冲量与轴线上位置的关系.
2.2 爆炸冲量径向分布
三维条件下柱形装药爆轰过程复杂,爆轰产物沿装药直径方向膨胀产生稀疏效应,加之爆轰产物与空气介质相互作用,爆炸冲量沿装药径向分布不均. 为研究柱形装药爆炸冲量与装药直径的关系,基于T. M. Сарамасин理论[21],作如下假设:
①装药瞬时爆轰,起爆后瞬时变为等体积爆轰产物,密度和外形与装药完全一致,内部压力均匀,且爆轰产物沿着原装药自由表面法向飞散;
②爆轰产物理想散射,且忽略空气对爆轰产物飞散的影响;
③装药爆轰完成瞬间,装药侧壁为绝对刚性,已获得初速但未发生运动,因此爆轰瞬间装药外壁的物质不运动,外壁形状与原装药形状一致.
基于上述假设,文献[21]中 САРАМАСИН提出了一种爆炸冲量理论计算方法,柱形装药对侧壁爆炸冲量可表示为
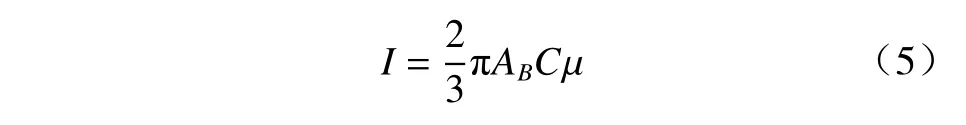
式中:AB为 炸药特性有关系数;C为装药质量; µ为装药形状系数,计算公式如下:

式中: ρ0为 装药密度;u0为 爆轰产物散射速度;D为炸药爆速;k为炸药爆轰产物的等熵指数,对高能炸药而言,k=3. 将式(6)~(8)带入式(5),则爆炸冲量与装药直径b的关系可表示为

基于式(9),林大泽[21]对圆柱装药的爆炸冲量进行了计算,结果表明,理论分析结果略低于实验值,但经修正可满足工程计算需求. 修正后炸药爆炸冲量可表示为

沿轴线方向,将柱状装药分割为若干微元,并通过圆柱近似替代截取的台体微元,得到炸药爆炸冲量ix与该处装药直径b的关系:
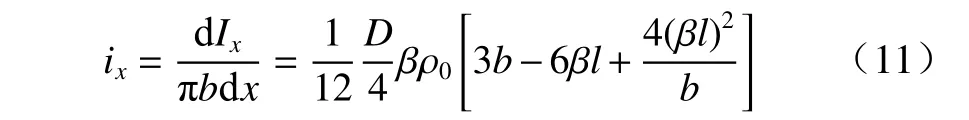
2.3 等冲量装药曲线理论模型
为使装药爆轰在轴线上产生大小一致的爆炸冲量,任一位置处爆炸冲量需满足以下关系:

式(4)和式(11)分别描述了爆炸冲量与装药轴线上位置和装药直径的关系,联立式(4)和式(11),将直径b=2r、相对位置 α=x/l代入其中,即可获得x和r的数量关系即等冲量装药曲线方程:

根据式(3)装药曲线上爆炸冲量一致时,各处破片的速度大小相等,破片速度可表示为

式中:v0为x=0 处的破片速度;为装药格尼系数;λ为战斗部装填系数. 在战斗部装药长度l确定的条件下,仅修正系数β对等冲量装药曲线线型产生影响. 对式(13)求解,获得装药曲线线型在不同修正系数β选择下的三维集合;通过给定不同修正系数β筛选得到内凹型装药曲线,将其绕r=0 旋转一周即可得到等冲量聚焦战斗部装药侧表面轮廓,筛选方法如图7 所示.

图7 修正系数筛选方法Fig.7 Selection method of correction parameter
预设装药长度分别为0.3、0.4、0.5 m 时,筛选出装药长度与修正系数相匹配的工况如表1 所示,装药曲线线型及对应工况装药外表面三维轮廓如图8所示.

表1 装药长度及修正系数筛选Tab.1 Selection of charge lengths and correction parameters

图8 修正系数对装药曲线线型影响及对应工况下装药外表面三维轮廓Fig.8 Effect of correction parameter on charge generatrix and corresponding charge shapes
3 破片飞散特性数值模拟
3.1 数值计算模型
线性聚焦式杀伤战斗部数值计算模型主要由等冲量聚焦曲线装药和预制破片两部分组成. 基于装药长度和修正系数匹配筛选结果建立战斗部模型,预制破片为直径为10 mm 的球形钨合金破片,破片采用轴向密排方式,破片列之间的重叠度γ=1,随着装药长度从0.3 m 增加至0.5 m,破片总数从360 枚增加至600 枚. 数值模拟模型如图9 所示.

图9 线性聚焦式杀伤战斗部数值计算模型Fig.9 Numerical model of linear focusing fragmentation warhead
主装药选择TNT 炸药,通过Mat_ high_ Explosive_ Burn 模型和JWL 状态方程描述TNT 炸药;空气采用Null 模型和Eos_ Linear_ Polynomial 状态方程描述;钨合金破片采用Mat_ Plastic_ Kinematic 模型描述. 各材料参数如表2~表4 所示[22−24].

表2 TNT 炸药主要材料参数Tab.2 Parameters for TNT explosive

表4 钨合金主要材料参数Tab.4 Parameters for tungsten alloy
计算过程采用ANSYS/LS-DYNA 软件,模拟过程选择ALE 算法,其中炸药、空气通过Euler 网格离散,预制破片采用Lagrange 网格离散,二者之间进行流固耦合. 装药径向和轴向网格大小均取1.0 mm;空气与装药相接位置划分方式一致,其他位置网格大小取2.0 mm;破片每条线段分两等份,每个破片共80 个网格. 计算域周围定义无反射边界,模拟真实战斗部爆炸工况.

表3 空气介质主要材料参数Tab.3 Parameters for air
3.2 典型破片驱动及分布特征
装药起爆、爆轰并开始释放能量,等冲量聚焦装药曲线调控装药爆轰能量的分配,使轴向破片受到基本一致的爆炸冲量作用并等速飞散,以上特征是等冲量曲线装药爆轰驱动破片毁伤目标的物质基础.在装药的聚焦驱动下,线性排布设计的破片形成速度基本一致的线性破片聚焦带,少量破片游离于聚焦带外,破片线性聚焦过程如图10~图12 所示,线性聚焦破片落点如图13 所示.

图10 破片飞散过程正视图Fig.10 Front view of fragmentation process
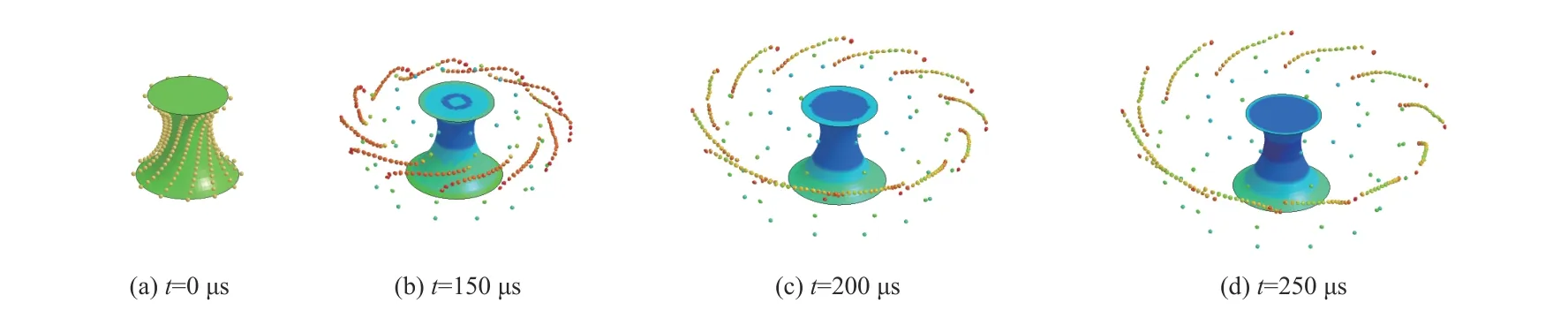
图11 破片飞散过程斜视图Fig.11 Oblique view of fragmentation process

图12 破片飞散过程俯视图Fig.12 Vertical view of fragmentation process

图13 线性聚焦破片落点分布Fig.13 Fall points of fragment
装药曲线等冲量设计通过聚焦带内破片的速度分布幅值F和标准偏差σ衡量,数值模拟中破片速度与理论值的偏差通过二阶中心距ξ衡量(以破片速度为样本,以理论值为数学期望). 破片速度分布幅值F表征聚焦带内破片速度与速度平均值之差的最大值与平均速度的比值,表示破片速度的分布范围,标准偏差σ表示分布范围内破片速度的离散程度,F、σ和ξ计算公式如下:
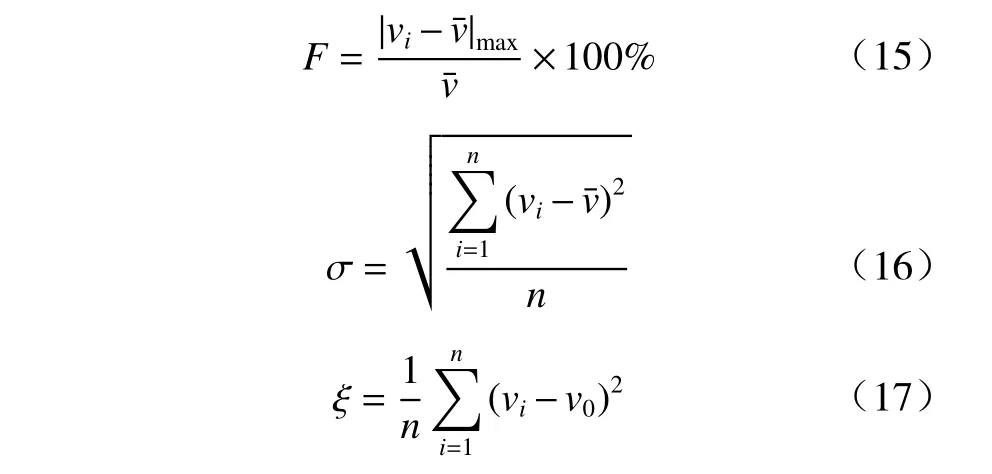
式中:vi为 聚焦带内任一破片速度;v¯为破片平均速度;v0为破片速度理论值;n为破片数.
3.3 装药长度影响
不同工况下7 m 处破片密度如表5 所示,修正系数为1.0 时,破片密度在装药长度为0.4 m 时达到最大值36 枚/m2,有显著的聚焦效应,修正系数为1.1和1.2 时,破片密度随装药长度增加而减小. 随着装药长度的增加,装药两端曲率增大,使破片在中近距离完成聚焦,在远距离处聚焦带宽度较大,破片密度较低,聚焦性能下降.

表5 7 m 处破片密度Tab.5 Density of fragments at 7 m
β=1.0 时,装药长度l对聚焦带内轴向破片速度分布、分布幅值和标准偏差影响分别如图14、图15所示,随装药长度增加,破片平均速度从1 333 m/s 增加至1 775 m/s,速度分布幅值从14.7%增大至17.1%;破片速度分布标准偏差从127.5 增大至147.0. 3 种装药长度条件下,破片速度理论计算值分别为1 450、1 755 和1 998 m/s,与数值仿真结果偏差分别为8.06%、10.98%和11.16%,表明仿真与理论计算结果吻合较好.

图14 装药长度对破片速度分布影响Fig.14 The effect of charge length on fragment velocity

图15 装药长度对F 和σ 影响Fig.15 The effect of charge length on F and σ
3.4 修正系数影响
装药长度为l=0.3 m 时,修正系数β对聚焦带内轴向破片速度分布、分布幅值和标准偏差影响分别如图16、图17 所示. 随修正系数β增加,破片速度平均值从1 333 m/s 增加至2 081 m/s,速度分布幅值从14.7%降低至9.2%;破片速度分布的标准偏差从127.5降低至105.6,离散程度降低. 3 种修正系数条件下,破片速度理论计算值分别为1 450、1 709、2 132 m/s,与数值仿真结果偏差分别为8.06%、7.61%、2.43%;二阶中心距分别为67 256、56 732、52 713 m2/s2,随修正系数增大,破片速度围绕理论值波动程度减小.

图16 修正系数对速度分布影响(l=0.3 m)Fig.16 The effect of correction parameter on velocity distribution of fragments(l=0.3 m)

图17 修正系数对F 和σ 影响(l=0.3 m)Fig.17 The effect of correction parameter on F and σ (l=0.3 m)
l=0.4 m 时,修正系数β对聚焦带内轴向破片速度分布、分布幅值和标准偏差影响如图18、图19 所示. 随修正系数β增加,破片速度平均值从1 560 m/s增加至2 153 m/s,速度分布幅值从16.6%降低至10.6%;破片速度分布的标准偏差从142.6 降低至103.7,离散程度降低. 3 种修正系数条件下,破片速度理论计算值分别为1 755、1 962 和2 244 m/s,与数值仿真结果偏差分别为12.11%、9.33%和4.05%;二阶中心距分别为172 102、114 790、91 049 m2/s2,随修正系数增大,破片速度围绕理论值的波动程度减小.
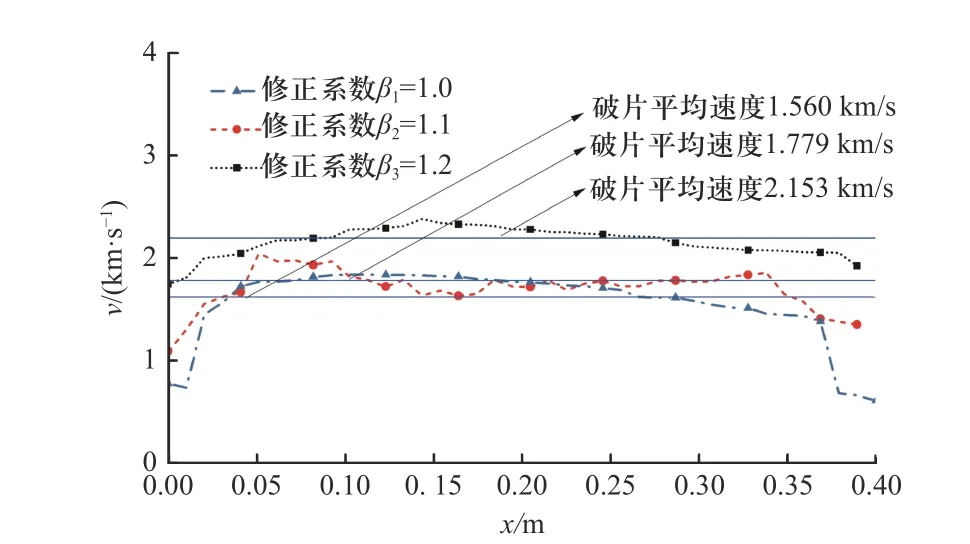
图18 修正系数对速度分布影响(l=0.4 m)Fig.18 The effect of correction parameter on velocity distribution of fragments (l=0.4 m)

图19 修正系数对F 和σ 影响(l=0.4 m)Fig.19 The effect of correction parameter on F and σ (l=0.4 m)
l=0.5 m 时,修正系数β对聚焦带内轴向破片速度分布、分布幅值和标准偏差影响如图20、图21 所示. 随修正系数β增加,破片速度平均值从1 775 m/s增加至2 713 m/s,速度分布幅值从17.1%降低至8.5%;破片速度分布的标准偏差从147.0 降低至126.4,离散程度降低. 3 种修正系数条件下,破片速度理论计算值分别为1 998、2 495 和2 803 m/s,与数值仿真结果偏差分别为11.19%、5.53%和3.21%;二阶中心距分别为125 971、112 876、108 915 m2/s2,且随修正系数增大,破片速度围绕理论值的波动程度减小.
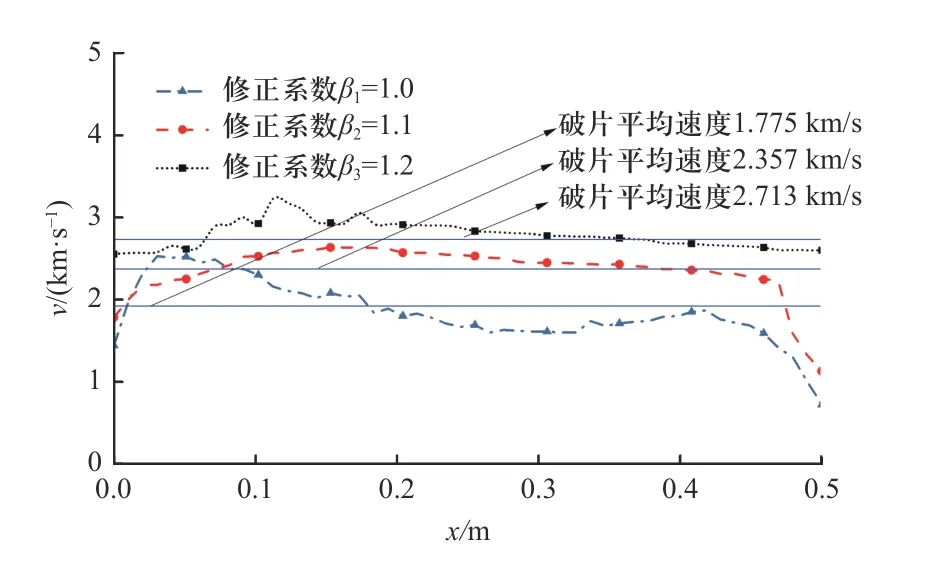
图20 修正系数对速度分布影响(l=0.5 m)Fig.20 The effect of correction parameter on velocity distribution of fragments (l=0.5 m)
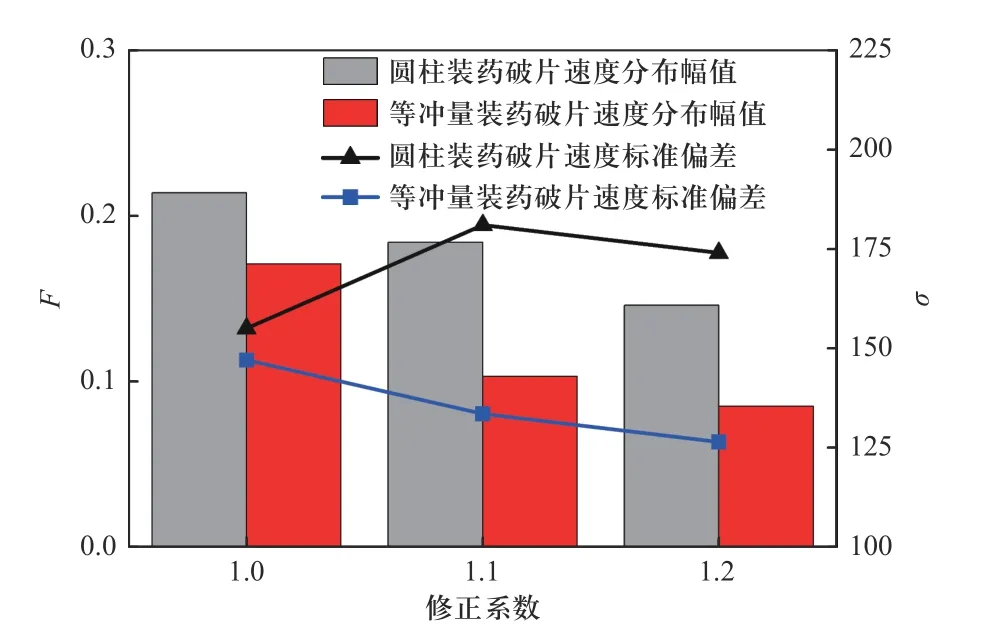
图21 修正系数对F 和σ 影响(l=0.5 m)Fig.21 The effect of correction parameter on F and σ (l=0.5 m)
如图8(a)、8(e)、8(i)所示,修正系数β调控了轴线上不同位置处装药曲线曲率,随着修正系数增大,装药曲线两端曲率减小,优化爆轰能量分配,使破片所受爆炸冲量基本一致,故破片速度分布幅值和标准偏差随修正系数增大而减小. 但装药两端破片排布较稀疏,爆轰产物泄露、能量利用率较低,使装药两端破片速度低于理论值. 位于装药中部的破片排布较紧密,爆轰能量利用率较高,因此位于中部的破片速度与理论值基本一致. 破片平均速度略低于理论值,这是理论计算并未考虑爆轰产物泄露导致的.
通过上述分析可知,无论采用何种装药长度,随着修正系数增加,聚焦带内破片速度整体呈增大趋势,破片速度分布的标准偏差均降低、离散程度变小,一定程度上说明了对长度采取修正开展研究的合理性. 对比于相同装药量、相同装药长度的圆柱形装药,采用等冲量装药曲线的速度分布范围、离散程度均显著减小,表明破片线性排布设计和装药曲线等冲量设计均可显著提升破片聚焦效应、减小破片飞散速度散布,从而最终有效提升破片杀伤战斗部毁伤威力.
4 结 论
本文主要针对线性聚焦式杀伤战斗部设计及破片速度飞散特性开展研究,获得的主要结论如下:
①通过线性聚焦式破片排布设计和等冲量装药曲线设计,可获得等速破片场并实现破片爆炸驱动下的线性聚焦.
②修正系数β=1 时,随装药长度由0.3 m 增加至0.5 m,聚焦带内破片平均速度从1 333 m/s 提高至1 775 m/s,速度分布幅值从14.7%增大至17.1%;破片速度分布标准偏差从127.5 增大至147;装药长度为0.4 m 时,破片密度达到最大值36 枚/m2.
③在装药长度一定条件下,随修正系数增加,装药曲线曲率增大,聚焦带内破片平均速度增大,速度分布幅值、标准偏差和破片密度均降低.
对比于相同装药量和长度的圆柱装药,采用等冲量装药曲线的线性聚焦式杀伤战斗部可产生等速破片飞散场,为增强破片聚焦效应提供了新的技术途径.

