台阶式溢洪道的 δ -LES -SPH 数值模拟

高仁祖， 吴海涛， 顾声龙*， 田丽蓉， 郑温刚

(1.青海大学 水利电力学院，西宁 810016；2.黄河上游生态保护与高质量发展实验室，西宁 810016)

1 引 言

溢洪道水流具有流速高和流量大等特点，为了保障大坝及下游安全，需要削减水流的动能。当水流流经台阶式溢洪道台阶表面时，水流会充分掺气并发生旋滚，水流处于湍流状态使得大小涡结构之间存在剪切作用，从而消杀水流所具有的巨大能量，达到消能目的。

为了全面评估台阶表面的复杂水流状况，并为设计实用提供可靠的信息，台阶式溢洪道的研究分为试验研究和数值模拟。赵相航[1]通过不同体型台阶式溢洪道的研究，分析了台阶上的水面线、流速以及压强等水力特性的分布规律。

相关研究表明，台阶式溢洪道消能显著，台阶上的流动结构比较复杂，自由表面的大变形以及水流破碎是研究台阶溢洪道的一大难题。光滑质点水力学(SPH)方法处理大变形以及水流破碎方面，尤其在捕捉自由水面方面比较有优势。SPH(Smoothed Particles Hydrodynamics)方法首次由Gingold等[2]提出，并成功运用到了流体动力学中。近20多年来，许多研究人员进行了完善和改进[3]，由于SPH方法在解决复杂的自由表面流上有独特的优势，因此，应用于许多流体动力学领域。如SPH方法应用于研究自由表面流[4]、气液固三相相互作用[5]及近海岸波浪破碎[6]等。

Husain等[7]采用开源的SPHysics程序及大水箱模型，研究了不同流量条件下台阶段上游水流区的压力分布。Gu等[8]利用ParellelSPHysics开源程序对不同体型的台阶式溢洪道进行了数值研究，采用推板模型稳定入流流量，研究了台阶上的水深、速度和压力变化。但是对于高雷诺数的湍流流动，需要考虑湍流带来的诸多影响，需要在SPH算法中加入一定的湍流模型来优化SPH算法。目前，常见的湍流模型有两方程k-ε模型[6,9]和大涡模型[10,11]。

Gotoh等[10]首次成功地把大涡模型加入不可压SPH方法中，并应用于近岸孤立波的数值模拟。Ting等[11]对后台阶流动进行了大涡模拟。Issa等[9]将RANS和LES模型分别加入SPH方法中，成功模拟了溃坝和近岸孤立波。随后，Di Mascio等[12]在 δ -SPH 方法的基础上提出了 δ -LES -SPH 模型。Meringolo等[13]运用 δ -LES -SPH 方法数值模拟了重力波，分析了波的生成、传播以及能量耗散随时间的变化。Meringolo等[14]又进一步对能量耗散进行了研究分析，数值模拟了水片入水池和溃坝。Tripepi等[15]用 δ -LES -SPH 方法研究了孤立波与水下方形障碍物之间的关系。

相关研究表明，具有湍流封闭模型的 δ -LES -SPH 格式可以改善数值耗散，并能得到更准确的计算结果。因此本文实现 δ -LES -SPH 方法的C++程序，并利用经典溃坝和宽顶堰进行验证，最后将 δ -LES -SPH 方法首次成功应用于台阶溢洪道水流的水力特性研究，这对消能防冲工的设计具有工程指导性的意义，为具体的工程实践提供有价值的参考。

2 δ -LES -SPH 模型

2.1 弱可压缩的N-S方程

在拉格朗日型式下的弱可压牛顿流体的N-S方程[14]表示为

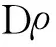
(1)

(2)

Dr/Dt=u

(3)

(4,5)

本文是基于粒子法，因此方程(5)为SPS(Sub -Particle -Scale)湍流模型，也称为Smagorinsky模式，在以往的大涡模拟[10]中，方程(5)用来封闭方程(4)，其中为应变率张量，=(u+uT)/2，为Kronecker张量，λ和为粘性系数，tr()为对应变率张量矩阵取迹，CS为Smagorinsky常数，Δ为粒子间距。弱可压缩SPH模型中，状态方程为[14]

(6)

(7)

2.2 δ -LES -SPH 模型

本文采用 δ -LES -SPH 模型，其中动量方程与连续性方程和文献[16]的 δ -SPH 格式相近，就是在连续性方程中加入了扩散项，动量方程中加入粘性项，目的是解决密度不连续带来的数值计算不稳定问题。δ -LES -SPH相比传统的SPH以及 δ -SPH 格式有许多优点，如δ -SPH中应用人工粘度，而 δ -LES -SPH 中应用了流体真实粘度；在 δ -LES -SPH 的连续性方程中，扩散项系数和粘性项系数的求解与SPS湍流模型建立关系。δ -LES -SPH方法的N-S方程[14]为

(8)

(9)

(10)

式中下标a和b为计算域内任意2个粒子，a为相对于粒子a坐标的梯度算子，Wa b为光滑核函数，本文使用Wendland C2核函数[17](光滑长度h=2dx,dx为粒子间距)，并将该核函数作为LES的滤波函数，a，ua，pa，ga和ra分别为第a个粒子的密度、速度矢量、压力、重力加速度和位置矢量，Va为a粒子影响域的面积(本文计算域Ω为二维)。相比于 δ -SPH 格式，扩散系数δ和粘性项系数α不再是常数，而是随a粒子和b粒子变化的变量，δa b可以表达为

δa b=2 [δaδb/(δa+δb)]

(11)

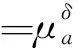
(12)

(13)

式中Cδ为一个常数，取1.5，lLES为SPH滤波过程的一个参考量(lLES=4dx，d/dx为分辨率，d为初始自由水面的高度)，应变率张量的计算公式为

(14)

(15)

(rb-ra)](rb-ra)/|rb-ra|2

(16)

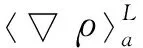
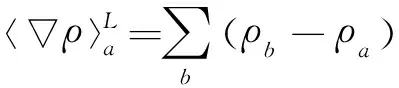
(17)

动量方程(9)中，粘性项πa b表达为

πa b=[(ub-ua)·(rb-ra)]/(rb-ra)2

(18)

方程(9)的粘性系数αa b为

αa b=α+2 [αaαb/(αa+αb)]

(19)

(20)

(21)

式中CS为Smagorinsky常数，CS=0.12，ν为液体的动力粘滞系数。用式(12，20，21)来封闭 δ -LES -SPH 模型，当研究剧烈自由表面流问题时，应变率张量在h趋近于0时，流体互相碰撞时会出现无穷值，为了使数值模拟过程稳定，根据文献[14]取αa<0.2，δa<0.2，其物理意义在于消除弱可压SPH数值模拟时带来的虚假数值振荡。

2.3 程序流程

本次开发的C++ δ -LES -SPH 模型程序的基本流程如图1所示。

图1 C++ δ -LES -SPH模型程序的基本流程

(1) 读取几何模型，并对几何模型(计算域)进行粒子化处理。

(2) 给每个粒子进行粒子配对，其邻近粒子搜索用到了链表搜索法。

(3) 遍历每一个粒子，通过式(17)进行密度梯度修正，以确保在自由液面处核函数粒子缺失条件下，密度梯度具有二阶精度，计算的结果参与步骤(6)的计算。

(4) 通过虚粒子法进行固壁边界处理，其中遍历每一个虚粒子，通过状态方程反推出其密度。

(5) 遍历每一个流体粒子，通过式(11，12，19～21)，求解出每个流体粒子的δa b和αa b，并参与当前时间步内的每个流体粒子密度变化量以及加速度的求解计算。

(6) 求解式(8，9)的左项(注：此程序中，没有提前遍历求解出每个粒子的核函数以及偏导数，而是每次遍历粒子需要时，才去求解该粒子的核函数以及偏导数)。

(7) 时间进程采用蛙跳法推进每一步求解，并且每500步输出一次文件。最终需要进行计算时间的判断，直到计算达到要求。

2.4 边界条件的处理

SPH方法中，靠近边界的流体粒子支持域内只有部分粒子，在固壁边界外无流体粒子，出现了积分边界截断的问题，造成边界附近的粒子穿过边界，因此需对固壁边界进行处理，以获得正确的计算结果。本文使用Adami等[18]提出的一种在流体外布置多层虚粒子实施固壁边界的方法，此方法直接将内部流体粒子的压力插值到虚粒子上，如式(22)，再利用状态方程反推出虚粒子的密度，虚粒子通过压力梯度对流体施加边界力，该边界处理方法可以很好地适应复杂几何边界问题。

(22)

式中ab为虚粒子的加速度。

3 算例验证

3.1 经典溃坝模型

本文采用经典溃坝算例进行验证，与文献[14,19]的模拟结果和Lobovsky等[20]的试验结果作了对比分析。如图2所示，初始的水箱长度L=5.367 m，布置L1为2 m和H1为1 m的矩形流体区域。流体粒子总数8万个，粒子间距为0.005 m，时间步长为10-4s，模拟总时长为10 s。

图2 溃坝数值模拟模型

图3分别给出了无量纲时间为t(g/d)1/2=1.41，5.24和6.41时的流态。图3(a)为文献[20]的试验流态，图3(b)为文献[18]的模拟流态，图3(c)为本文的模拟流态。通过 δ -LES -SPH 数值模拟的流态与试验的流态以及传统SPH模拟得到的流态比较分析，发现数值计算过程稳定，δ -LES -SPH 相比传统的SPH方法，其数值模拟的流场更加明显地反映了溃坝真实流动情况，说明 δ -LES -SPH 可精确捕捉自由水面。

图3 t (g/d)1/2=1.41，5.24和6.41(从上到下)时的流态

图4给出了t(g/d)1/2=9.45的αa值和δa值的模拟结果，其中Ma=0.05，在图3的流体区域发生了翻滚水流的猛烈撞击，耗散项主要作用于自由表面重联和破裂而产生的涡旋周围，此时αa值和δa值表现得很高，在大部分流体区域，αa值和δa值都接近于零。这些现象与文献[14]的结果一致。在3.1节中，知道αa项和δa项都与应变率张量成正比关系，因此，这两项的变化值都出在了同一个图中。整个计算域中，αa和δa的平均值为0.005和0.1。图5给出了t(g/d)1/2=20时的涡量图，并以无量纲涡量进行了分析，图5出现了诸多湍流漩涡斑点。

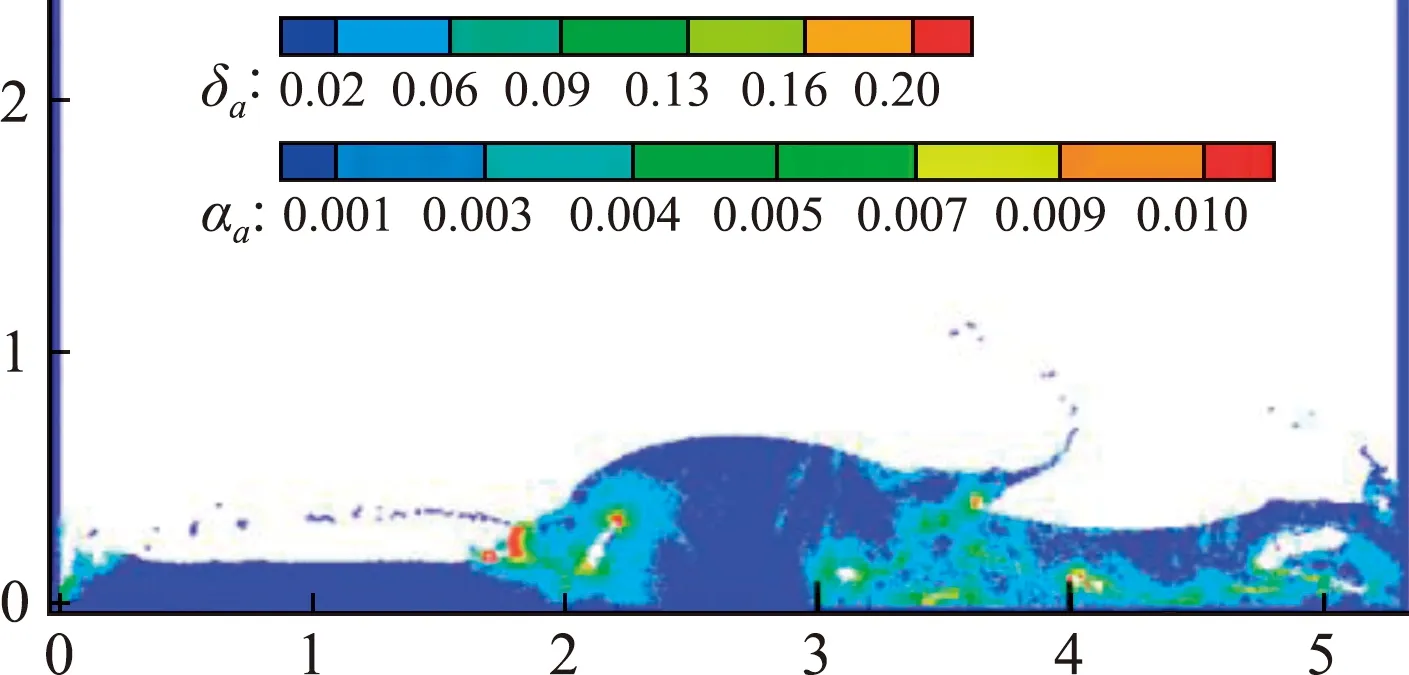
图4 t (g/d)1/2=9.45的αa值和δa值的模拟结果

图5 t(g/d)1/2=20时的涡量

图6是t(g/d)1/2=1.079和1.75时的不同粒子间距下的自由水面曲线，选择这两时刻的原因是此时的溃坝流态比较稳定。其中dx表示粒子间距，纵横坐标表示自由水面上粒子的水平和垂直距离。可以看出，当粒子间距变小，粒子数量变多时，同一时间下，自由水面明显呈收敛趋势，图6中dx=0.005和0.0025的自由水面基本一致，然而在同一工况下，dx= 0.005的模拟时长需要3天，而 dx=0.0025的模拟时长需要10天，最后两者的模拟结果基本一致，为了节省计算时间，dx=0.005 作为最优粒子间距进行后面的案例分析。

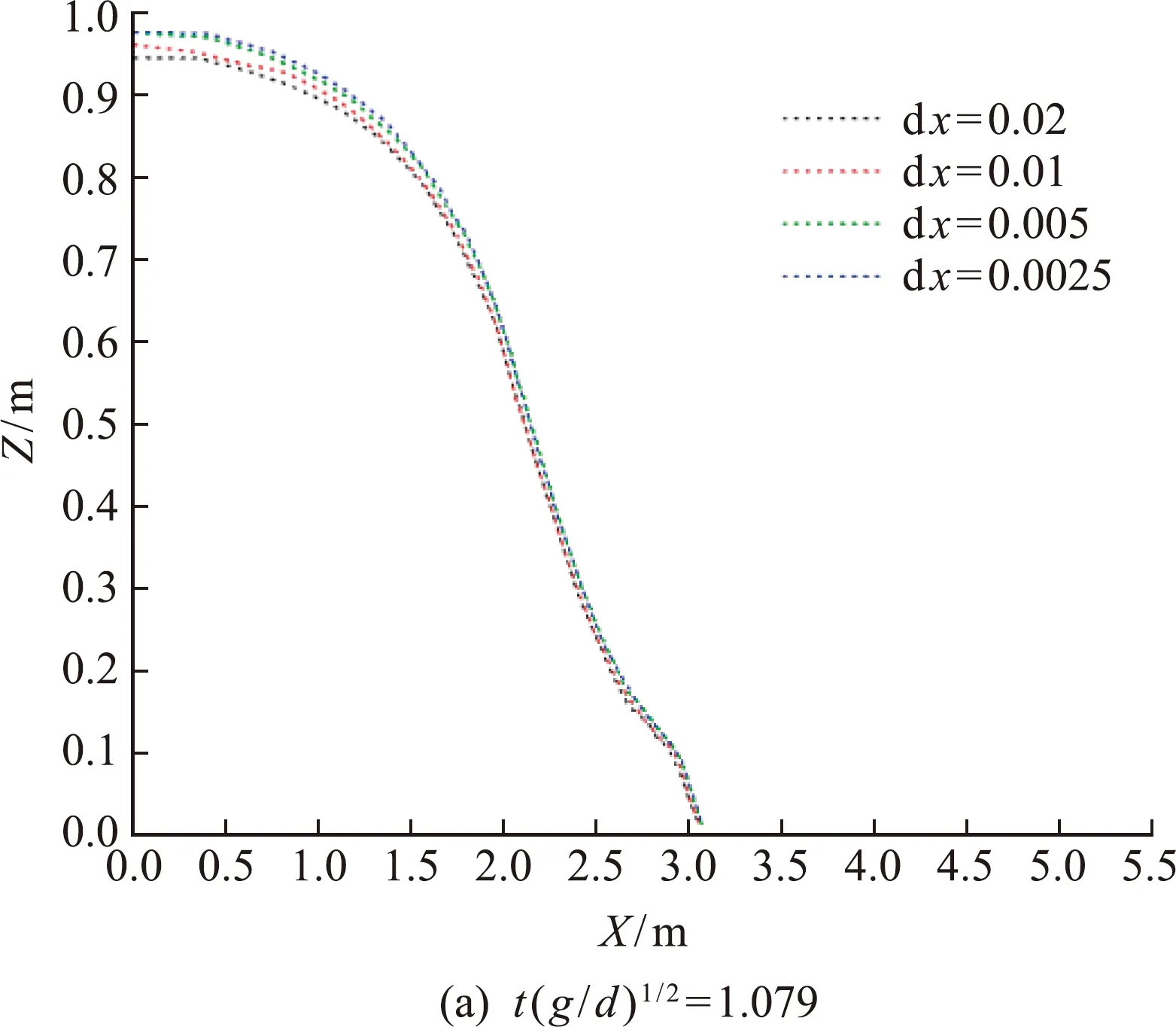
图6 t (g/d)1/2=1.079和1.75时的不同粒子间距下的自由水面曲线

综上所述，本节模拟的结果以及相应的对比分析，说明了自主实现的 δ -LES -SPH 算法具有稳定性以及可靠性。

3.2 宽顶堰的验证

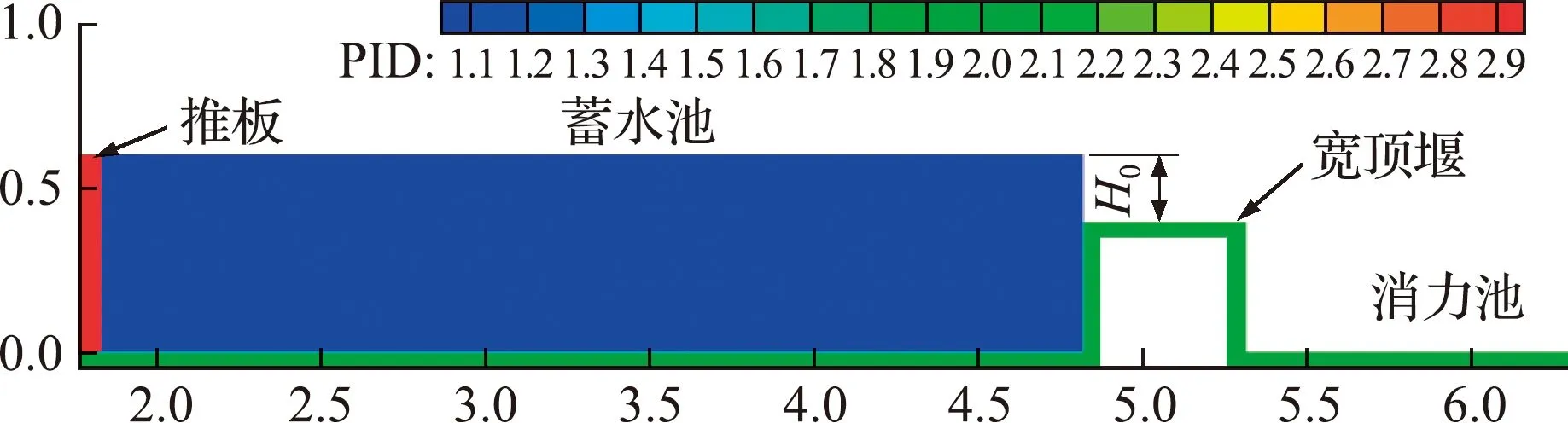
图7 宽顶堰数值模拟模型

图8 流量随时间变化的曲线

图9给出了t=6 s时沿水平方向的流速分布云图，可以看出，水流受到宽顶堰方形堰角的影响，在堰顶上游局部区域的水平速度为负，说明该区域发生了回流现象；水流流过堰顶流入消力池中，水舌下面区域的流速分布极不均匀，说明水流发生了旋滚以及回流现象且自由水面波动较大，在水舌下面区域的水流受到漩涡以及水质点相对运动的影响，加剧了水流能量耗散，使得此区域的水流流速急剧下降。

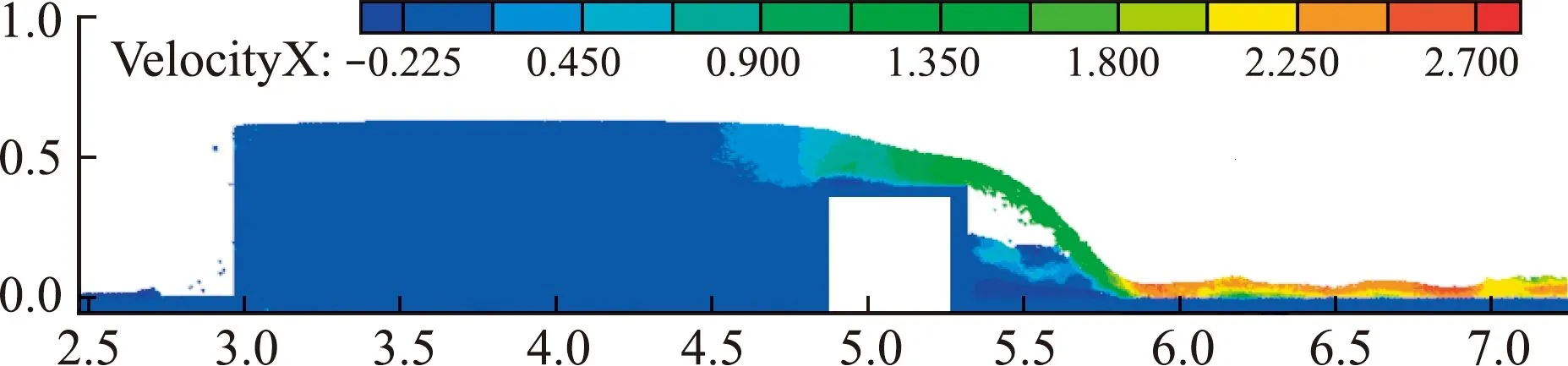
图9 t =6 s时沿水平方向的流速分布云图

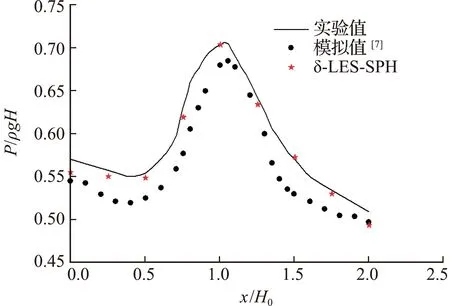
图10 沿堰顶表面水平方向的压强变化曲线

通过宽顶堰的数值模拟以及结果分析可知,本次对 δ -LES -SPH 模型的实现，考虑了湍流这部分因素对计算带来的影响，有效改善了数值计算结果。

3.3 台阶式溢洪道的数值模拟

表1 模型相关参数

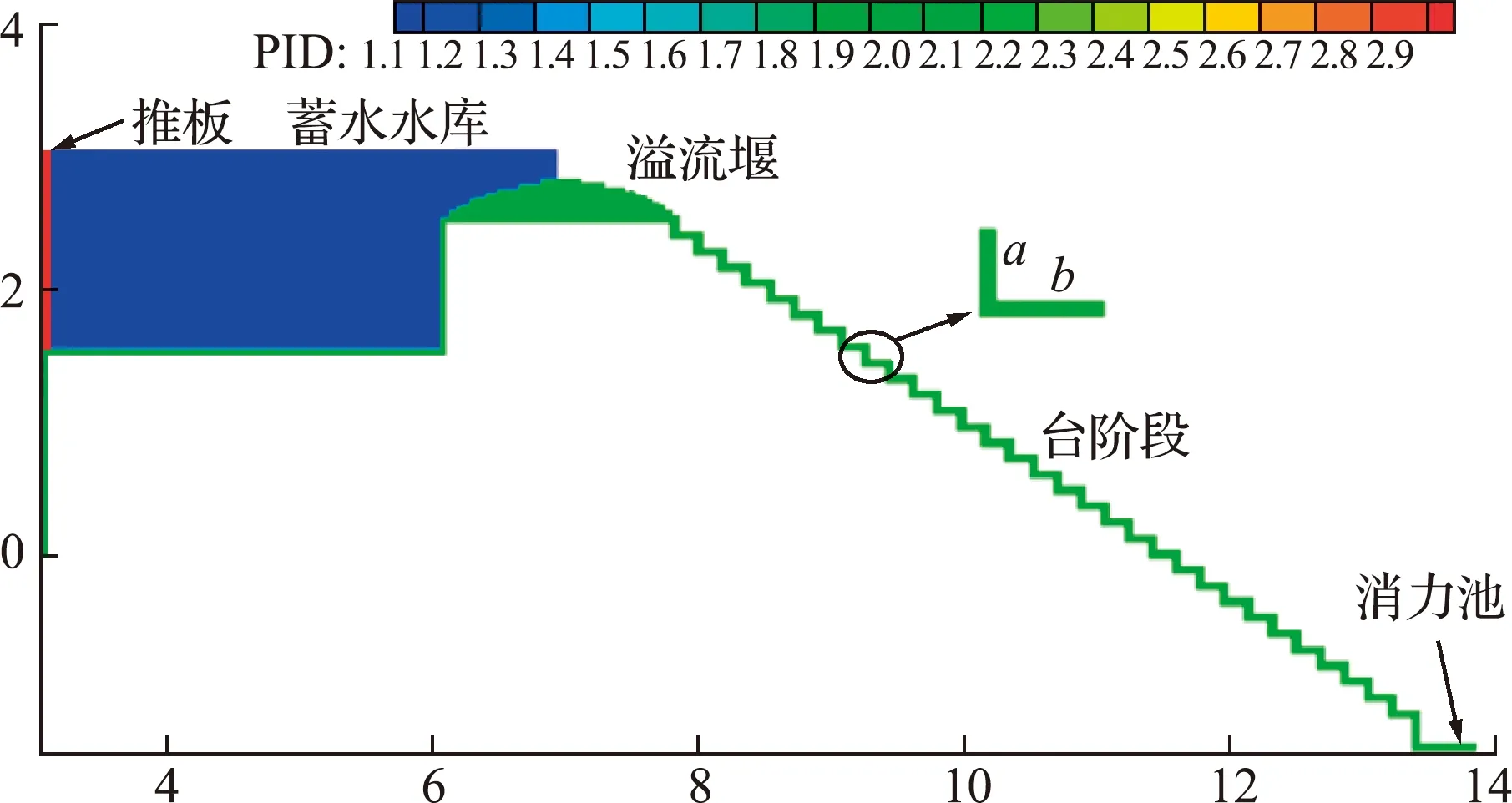
图11 台阶式溢洪道的数值模型

图12给出了31阶溢洪道在t=8.4 s时的水流流态，可以看出，台阶上游段的水面基本平稳，台阶下游段水面破碎严重，水深略有缓慢上升趋势，这与试验观测的水面现象相近。水流过台阶端角时出现了局部空化现象，而空腔上部水流为挑射流，如图12(b)[1]试验中也能观察到局部空化现象，与试验中观察到的吻合，模拟中的31阶溢洪道上的水流流态为跌落水流，因此会对台阶造成较大的冲击和冲刷。

图12 31阶溢洪道在t =8.8 s时的数值模拟水流流态和31阶溢洪道试验时的水流流态

图13给出了t=8.4 s的31阶和8.8 s时的26阶溢洪道的水深试验值[1]和 δ -LES -SPH 大涡模拟值的沿程水深曲线，图中横坐标无量纲化为x/L,坐标L为溢洪道长度是70 m,x为监测点到堰顶的水平距离，h为沿程水深，结果表明,图13(a)与无湍流模型的开源DualSPHysics的31阶模拟值[22]相比，开源DualSPHysics的模拟值与试验值的平均误差为4.40%。溢流堰上的水深变化先逐渐降低，进入台阶段水深又明显增加，随后水深变得平稳。31阶溢洪道台阶段上模拟的水流水深最大值为0.785 m，发生在台阶30附近，水流趋于平稳后，水深达0.76 m，沿程的模拟水深值与试验水深值的平均误差约为4.20%，提高了4.55%的计算精度(精度计算是两误差之差除以原平均误差)。其26台阶溢洪道上最大水深模拟值为0.869 m，水流趋于稳定时，水深维持约在0.8 m左右，模拟水深与试验水深的沿程平均误差约为4.23%,这里提到的误差是通过各个监测点处的误差求和再求平均得到。

两种工况的对比结果表明，δ -LES -SPH 数值模拟和试验值的结果吻合度较高，说明 δ -LES -SPH 能够较为准确地反映台阶式溢洪道上水面的变化趋势以及形态。

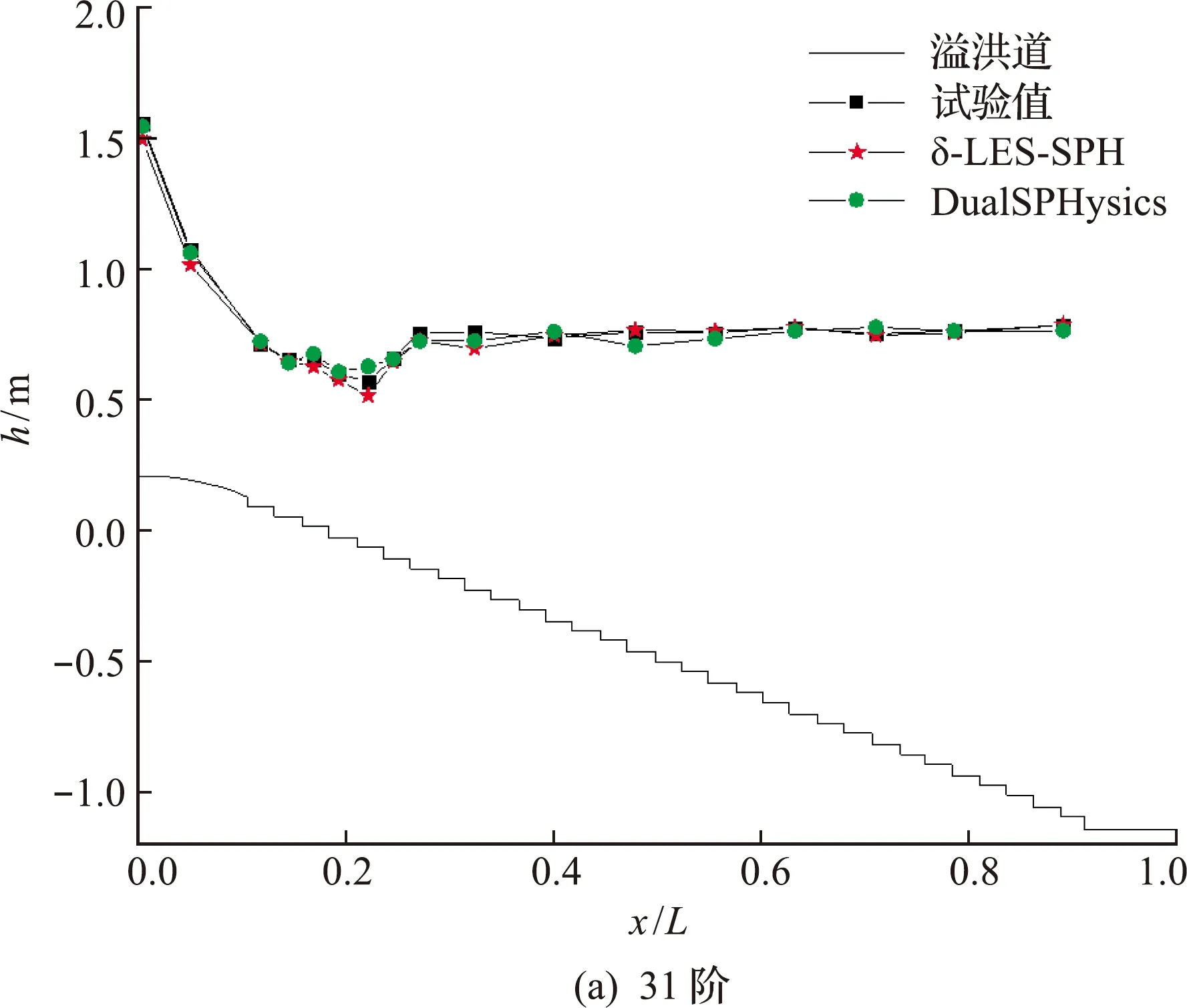
图13 31阶和26阶溢洪道的水深试验值和模拟值的沿程曲线

图14给出了t=8.4 s的31阶和8.8 s时的26阶台阶式溢洪道流速的试验值[1]和模拟值的沿程曲线变化，图14与无湍流模型的开源DualSPHysics的31阶模拟值[22]都以相应比例转化为原型数据作了比较，分析得出，堰上的水流流速是先沿程增大，在台阶段增大到最大值又会沿程减小，随后流速略有增大或减小的趋势呈波浪状分布，其试验值和 δ -LES -SPH 模拟值以及DualSPHysics模拟的流速沿程分布趋势一致。

图14 31阶和26阶溢洪道的流速试验值和模拟值的沿程曲线

试验的最大流速为13.8 m/s,δ -LES -SPH 模拟的31阶溢洪道的最大流速为13.9 m/s，试验值和DualSPHysics的模拟值沿程平均误差约为6.10%，其试验值和本文的模拟值沿程平均误差约为3.00%，提高了50.82%的精度；26阶溢洪道模拟的最大流速为15.64 m/s，试验中最大流速为14.993 m/s，其试验值和模拟值沿程平均误差约为4.60%。

比较 δ -LES -SPH 和DualSPHysics[22]的结果，发现 δ -LES -SPH 的模拟结果与试验结果吻合度较高，尤其在台阶下游段 δ -LES -SPH 试验的流速都呈波浪形分布，而DualSPHysics的流速曲线表现较为平稳，反映了 δ -LES -SPH 方法在曲线变化的拐点处具有很好的修正作用，在Tripepi等[15]用 δ -LES -SPH 方法研究孤立波与水下方形障碍物之间的关系时，也同样提到了这一作用。

图16对t=8.4 s的31阶和8.8 s的26阶台阶式溢洪道的消能率进行研究分析，分析得出，消能率的变化从堰顶向下游沿程增加，其试验值[1]和 δ -LES -SPH 模拟结果沿程分布趋势一致,而且从整体趋势来看，相比较开源DualSPHysics方法模拟得到的结果，31阶中 δ -LES -SPH 模拟值与试验值吻合较好，计算消能率的公式为

(23，24)

(26)

式中E1和E2分别为1-1断面和2-2断面的总能量,H0为2-2断面到溢流堰堰顶的垂直距离,H1为水库水位到溢流堰堰顶的垂直距离，h2和v2分别为2-2断面的水深和流速，g为重力加速度,ΔE为损耗能量，α为溢洪道坡度，具体如图15所示。

图15 消能断面选择

对于31阶溢洪道，试验中最终的消能率为76.05%，通过开源DualSPHysics方法[22]模拟的结果分析得到的消能率为78.34%，与试验值作比较，消能率的误差约为3.01%；通过 δ -LES -SPH 数值模拟的消能率为75.89%，与试验值作比较，消能率的误差约为0.29%，在SPH方法中实现大涡模拟，使得模拟结果提高了90.37%的精度。对于26阶的溢洪道，试验中最终的消能率为 75.35%，通过 δ -LES -SPH 模拟的消能率为74.72%，与试验值作比较，消能率的误差约为0.26%。图16中 δ -LES -SPH 数值模拟得到的消能率相比DualSPHysics方法得到的结果略偏小，这是因为DualSPHysics用的是人为调节扩散项和耗散项的 δ -SPH 模型，而 δ -LES -SPH 用大涡湍流模型封闭了人为调节的扩散项和耗散项，因此扩散项和耗散项的变化与实际流场有关。由以上模拟结果来看，在计算中比 δ -SPH 模型要精细很多。DualSPHysics方法与 δ -LES -SPH 方法的边界条件不同，然而边界条件的给出是为了阻止流体粒子穿透固壁边界，而对计算结果影响甚小。

综上所述，通过曲线变化趋势的比较以及相应的平均误差分析可知，在具有复杂湍流性质的SPH数值模拟中加入 δ -LES -SPH 模型，优化传统SPH算法，使得数值模拟过程稳定，且精确了模拟结果。以上结果也表明缩小比例尺后的数值试验没有对原有试验产生影响。此次台阶式溢洪道数值模拟进行28核并行处理计算，一组工况花费了大约15天的时间,DualSPHysics方法一组工况在32核处理计算需要1天时间，相比之下添加复杂湍流模型，反而增加了所需模拟时间。

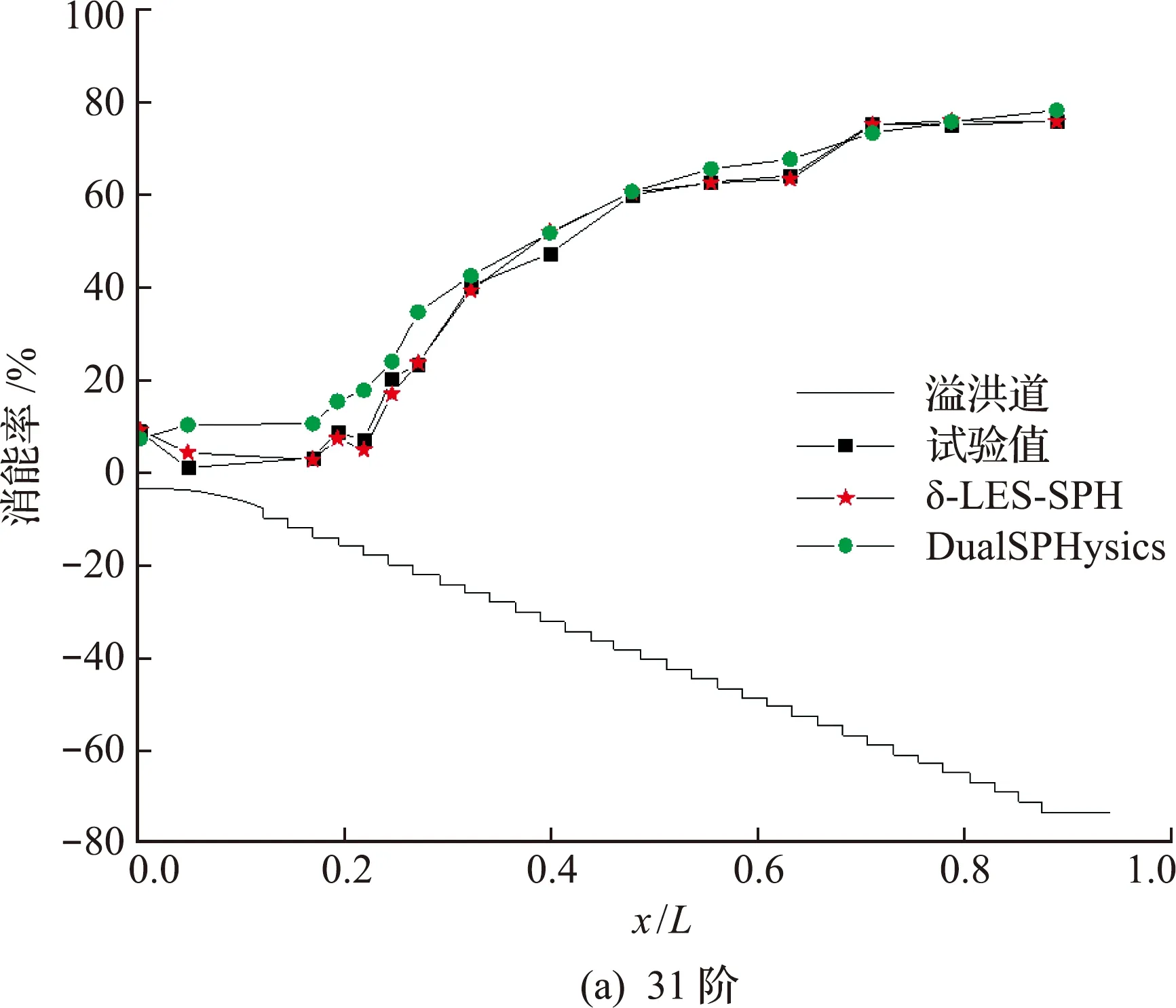
图16 31阶和26阶溢洪道的试验值和模拟值的消能率沿程曲线

4 结 论

本文就基于Mascio提出的大涡模型思想，自主实现了 δ -LES -SPH 程序，并通过溃坝案例与宽顶堰案例验证了 δ -LES -SPH 程序，验证结果表明，该算法在湍流流动数值模拟过程中具有较好的准确性与稳定性。最终，用 δ -LES -SPH 程序首次数值模拟两种阶数的台阶式溢洪道，并与现有文献对比分析得出以下结论。

(1) δ -LES -SPH 方法可以很好地捕捉其自由水面，能够准确地反映其台阶上复杂变化的水流流态，台阶上的各断面水深、各断面的水流流速以及消能率的变化趋势总体与试验趋势一致。31阶的最大流速为13.9 m/s，出现在第20级台阶上，26阶的最大流速为15.64 m/s，出现在第4级台阶上。

(2) 对31阶台阶式溢洪道数值模拟，与无大涡模型的DualSPHysics方法比较，提高了沿程水深4.55%的精度、流速50.82%的精度、效能率90.37%的精度，而且在曲线拐点附近 δ -LES -SPH 的曲线变化更接近于试验值，对曲线拐点处的数值结果有很好的修正作用，充分体现了 δ -LES -SPH 的优势。

(3) 由消能率的数值结果分析可知，台阶式溢洪道上的消能率沿程逐级增大，最后趋于稳定，31阶和26阶的消能率分别达到了75.89%和74.72%，明显31阶在消杀下泄水流的能量方面优于26阶，充分体现了台阶式溢洪道的消能效果。这些数值结果对消能防冲工的设计具有指导性的意义，本文首次在台阶式溢洪道方面使用 δ -LES -SPH 方法，这是在具有复杂湍流流动研究方面的探索，也是创新，为未来开发高效的算法提供有价值的思路。