基于修正Park-Ang模型的圆钢管构件地震损伤评估

刘 翔， 朱南海， 陈禄军

(江西理工大学 土木与测绘工程学院，赣州 341000)

1 引 言

大跨度空间网格具有结构自重轻和整体性能好等优点而广泛应用于火车站和体育场馆等大型建筑中[1]，圆钢管是该类结构常用的杆件形式。各杆件通过节点相互连接形成结构整体，为保证结构在服役期间的安全性能，在设计初期需要考虑结构从构件层面到结构层面的失效劣化过程[2]。地震作用是造成结构倒塌破坏的重要因素之一，而且结构的破坏往往始于薄弱构件和节点，因此对结构进行有效的损伤性能评估对保证结构的安全性显得尤为重要[3]。强震作用下的损伤破坏指数可以直观描述结构或构件的损伤情况，可为结构的安全性能评估和建立合理的结构损伤判别准则提供依据[4]。

基于损伤性能的抗震设计，在设计阶段可根据不同地震作用下的构件损伤程度来优化构件的几何尺寸等参数，使结构能够兼顾成本与预期的抗震性能目标，因此如何描述结构的损伤演化过程与损伤程度成为当前抗震设计研究领域的热点之一[5]。李永梅等[6]基于损伤理论和能量原理，提出以塑性耗能指标衡量结构整体或者局部的损伤状态。姚姝等[7]设计多个单层网壳结构模型，通过切断单根杆件模拟实际杆件损伤，通过网壳结构损伤前后的加速度响应，建立损伤杆件位置识别指标向量，识别出实际结构的损伤位置。门进杰等[8]通过修正Park-Ang双参数地震损伤模型建立了适用于RCS混合框架结构的地震损伤模型。Brescia等[9]通过研究多组钢构件和钢框架结构的变形能力，得出钢构件的单调加载变形能力与累积变形能力间的变化规律。杨游等[10]对框架结构进行动力增量分析，对比了六种不同损伤模型的差异性以及结构层数和设防烈度对结构性能的影响。漆启明等[11]基于多组钢筋混凝土空心墩的拟静力实验结果，对空心墩结构的损伤演化过程以及破坏机理进行分析，利用裂缝、钢筋应变和损伤分量等参数划分出构件的性能水准及其对应的破坏形态。Cao等[12]基于大量高铁桥墩构件的拟静力试验，通过考虑构件纵筋配筋率与轴压比对损伤模型的影响，建立起适用于评估高速铁路桥墩结构损伤状态的双参数地震损伤模型。

本文针对常用的圆钢管构件，基于Park-Ang地震损伤模型，研究该类构件的地震损伤评估方法。通过对Park-Ang双参数地震损伤模型的累积滞回耗能项进行修正，得到适用于评估薄壁圆钢管构件的双参数地震损伤模型，而后基于圆钢管构件在低周反复荷载作用下的滞回曲线，研究损伤模型组合系数与构件参数间的变化关系，建立圆钢管构件的双参数损伤判别准则，提出圆钢管构件的损伤性能水准划分标准，给出圆钢管构件在不同破坏状态下的损伤指数变化范围。

2 修正的Park-Ang双参数损伤模型

Park等[13]基于钢筋混凝土梁柱构件拟静力试验，提出了一种可以同时考虑构件最大变形量与累积滞回耗能的构件双参数损伤评估模型——Park-Ang损伤模型，其表达式为构件最大位移和累积滞回耗能两参数的线性组合，即

(1)

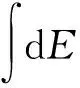
(2)

由于Park-Ang损伤模型并不能反映出构件极限滞回耗能与累积幅值之间的关系，当构件单调加载至破坏时，计算出的损伤指标不收敛于1，且构件在弹性阶段反复加载时，损伤指标不收敛于0，因此需要对损伤因子的收敛性问题做进一步研究[14-16]。模型中两种参数采用的线性组合方式形式简单，便于描述，但是缺乏理论依据，若采取非线性组合方式则更为合理，但其中的组合参数不易确定[17]。

Chai等[18]将损伤模型中累积耗能项的分子中减去单调加载下的耗能值，对损伤模型进行修正，可实现损伤指标收敛于1.0，修正后构件损伤模型的表达式为

(3)

式中Eh m为构件单调加载下的塑性耗能，其他参数同式(1)。

王东升等[19]考虑了构件的弹性工作阶段对于双参数损伤模型中位移项和能量项的影响，提出了改进的Park-Ang损伤模型，其表达式为

D=(1-β)[(δm-δy)/(δu-δy)]+

β{∑βiEi/[Fy(δu-δy)]}

(4)

式中Ei为第i个滞回圈的滞回耗能,βi为能量项加权因子,其他参数同式(1)。

陈林之等[20]提出在能量参数项中减去构件的弹性阶段耗能，修正后的表达式为

(5)

式中各项参数与式(1)所示的Park-Ang损伤模型相同。

周知等[21]基于原始的损伤模型，在大量型钢构件滞回试验的基础上，提出适用于箱型截面和工字型截面钢构件的修正损伤模型，其表达式为

D=(1-βs)[(δm-δy)]/(δu-δy)+

(6)

式中βs为与构件轴压比、长细比和翼缘高厚比等相关的组合系数公式。

3 圆钢管构件的修正Park-Ang损伤模型

3.1 圆钢管构件的损伤模型

为了使Park-Ang损伤模型能够适用于圆钢管构件的损伤评估，需对该损伤模型做进一步改进。考虑到圆钢管构件在弹性阶段内不会发生塑性损伤情况，因此圆钢管构件在循环加载过程中不考虑弹性阶段的耗能，将式(6)所示损伤模型中的累积耗能减去加载初期阶段产生的弹性耗能，得到修正后的损伤模型为

D=(1-βc)[(δm-δy)/(δu-δy)]+

(7)

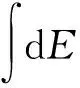
图1中Fe为构件首次屈服时的荷载值，取构件的屈服荷载与0.75倍极限荷载的较小值，点B为构件的屈服位移δy与屈服荷载Fy组成的坐标点。单调加载下的极限位移确定方式如图2所示，其中Fmax为构件单调加载下的最大荷载，点J对应横坐标为极限位移δu，其值取0.85倍的极限荷载对应的位移值。

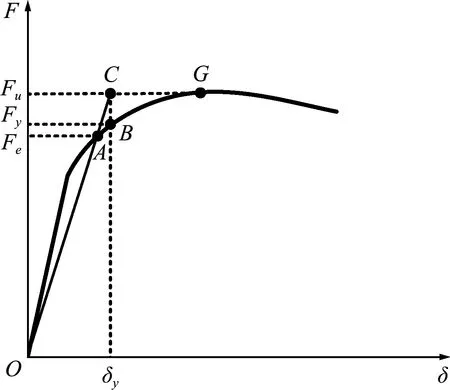
图1 屈服位移的确定方法

图2 极限位移的确定方法

3.2 组合系数的确定

为建立适用于圆钢管构件的损伤模型，需考虑钢管构件不同参数(径厚比、轴压比和长细比)的影响以获得式(7)的组合系数βc。组合系数βc可根据构件在达到破坏极限坏状态时其损伤指数达到 1.0 进行反推求得，当D=1.0时，由式(7)可得

(8)

组合系数可直观反映圆钢管构件在反复荷载作用下的累积耗能能力。式(8)中δy和δu可根据多组圆钢管构件在低周反复荷载作用下的滞回曲线和骨架曲线(各级循环加载的峰值点连接成的包络线)按照图1和图2所示方法进行计算，进而得到每根钢构件对应的组合系数βc，进而采用回归分析方法可得组合系数与构件参数间的变化规律。

为得到圆钢管构件的恢复力特性曲线，施加的荷载形式为轴力和循环弯矩，循环弯矩施加规则按照ECCS的加载制度以构件的屈服位移进行控制，在构件处于弹性状态下施加等幅荷载并循环一周，然后逐级提高位移幅值并循环三次，钢管屈服位移可按照式(9)计算得到[23]。

(9)

式中fy为钢材的屈服强度设计值，E为钢材的弹性模量，y为圆钢管构件外边缘至截面几何中心的长度，n为构件轴压比，L为构件计算长度。

根据网壳结构技术规程(JGJ61-2003)[24]规定，杆件的容许长细比为150且横截面尺寸不宜小于Φ45×3，钢结构设计标准(GB50017)[25]规定圆钢管受压构件的外径与壁厚之比不应超过100，钢管壁厚不应超过25 mm，选取横截面直径(外径)为219 mm，壁厚分别为6,8,10和12，即径厚比(d/t)分别为36.5,27.4,21.9和18.3的圆钢管构件作为分析对象，取构件的轴压比(n=N/Afy)分别为0.2,0.4和0.6。各圆钢管构件的参数及由式(8)计算获得的组合系数值列入表1。

表1 圆钢管构件主要参数及组合系数值

图3所示为钢管构件分别在加载初期阶段、中期阶段和后期阶段的应力分布以及变形情况，随着位移荷载的不断增大，端部约束区域逐渐从弹性状态进入弹塑性状态，并在底部出现轻微的鼓曲现象，构件在加载后期阶段出现严重的起鼓现象导致刚度下降，承载能力降低。图4为构件在循环荷载作用下得到的滞回曲线。

图3 三个加载阶段的应力

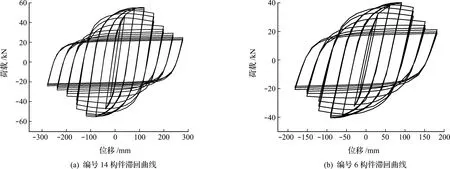
图4 循环荷载作用下的构件滞回曲线

由表1可知，通过反推法得出的组合系数其计算值与圆钢管构件径厚比、长细比和轴压比变化密切相关。组合系数的大小反映了圆钢管构件的延性性能以及在反复荷载下的耗能能力，构件滞回耗能能力越强，组合系数值越小，构件滞回耗能能力越弱，组合系数值越大。图5和图6为圆钢管构件的组合系数值在不同截面参数下的变化曲线。

图5为圆钢管的径厚比分别取36.5,27.4,21.9和18.3时，在不同轴压比和不同杆件长度下组合系数βc的变化情况。如图5(a)所示，当圆钢管的径厚比为36.5时，随轴压比的增大，在不同构件长度下，组合系数βc均呈下降趋势，同时可以看出构件长度也是影响组合系数βc的因素之一，长构件的组合系数βc低于短构件，说明构件的耗能能力随其轴压比和长度的增大而增大。这是因为对于压弯构件而言，轴压力的存在有利于构件抗弯能力的提高，构件耗能能力随之增强。同理，由图5(b)可以看出，当圆钢管构件的径厚比为27.4，组合系数βc与轴压比和构件长度之间具有相同的变化规律。进一步当圆钢管构件的径厚比取为21.9和18.3时，其组合系数βc与轴压比和构件长度之间具有相似的变化趋势。

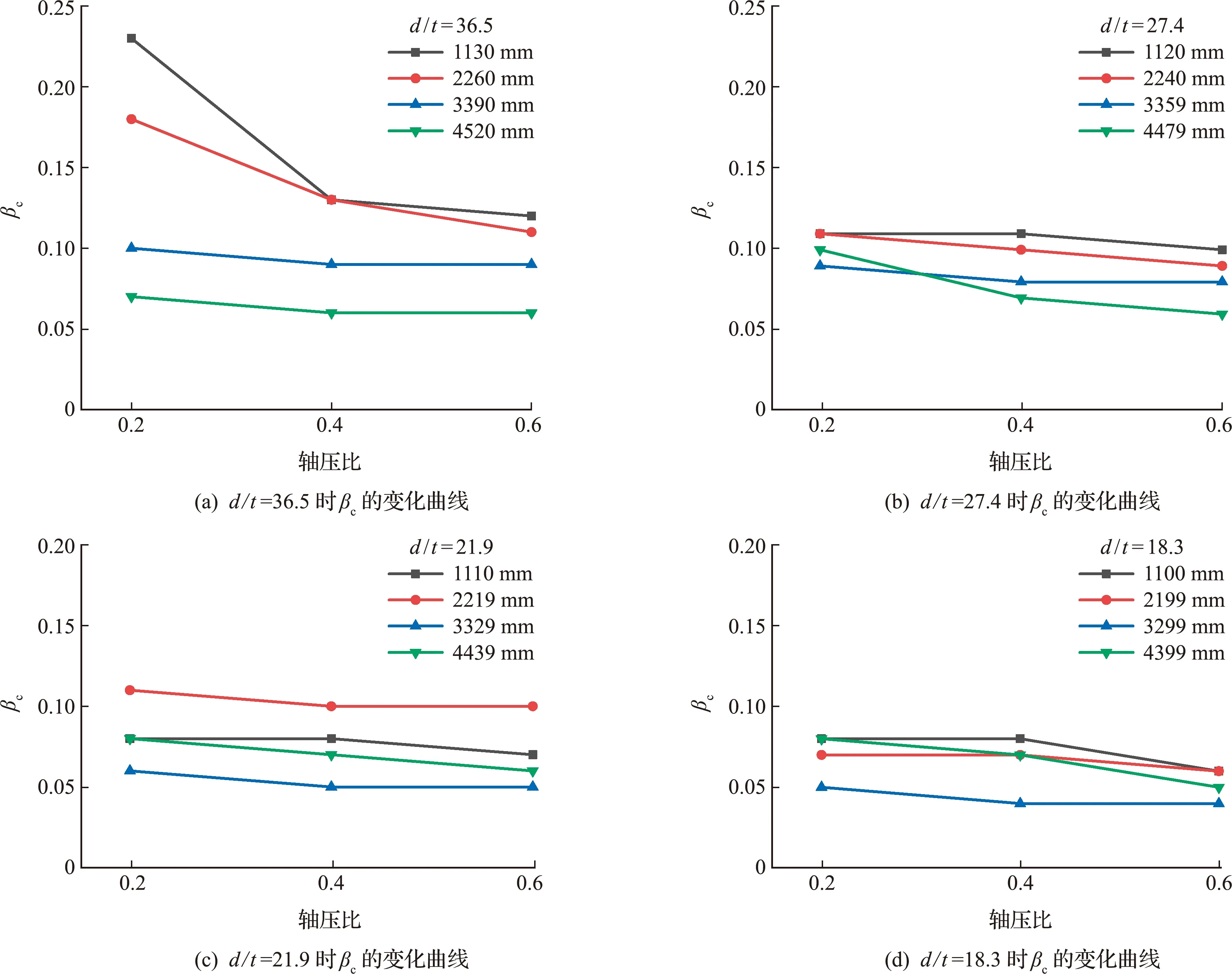
图5 不同轴压比下的组合系数变化情况

图6 不同径厚比与杆件长度下的组合系数变化情况

图6为圆钢管构件的轴压比为0.4时，构件的组合系数βc随径厚比和长度的变化曲线。如图6(a)所示，随径厚比的增大，构件的组合系数βc也逐渐增大，同时从图6(b)可以看出，随构件长度的增大，构件的组合系数呈减小趋势。表明低径厚比构件其耗能能力高于高径厚比构件，且长构件高于短构件。因此为保证圆钢管构件的耗能能力，对于较短的钢管构件可采用小径厚比，对于长度较长的构件可采用大径厚比。

表1给出了具有不同参数的构件对应的组合系数，在此基础上采用线性回归方法建立组合系数βc的计算值与构件参数间的关系，得到组合系数βc与构件参数的关系式为

βc=-0.0355n0-0.00126λ+

0.00288(d/t)+0.05854

(10)

式中n0为轴压比，λ为长细比，d/t为径厚比。为验证该式拟合结果的准确性，将组合系数的计算值与拟合值进行比较，结果如图7所示。

图7(a)为组合系数值的计算值与拟合值的分布情况，可以看出，两值分布于45°线附近，具有明显的相关性；图7(b)为计算值与拟合值之间的绝对差值分布情况，可以看出计算值与拟合值相差较小，通过计算Pearson相关性系数得到二者的相关性系数为0.713，表明计算值与拟合值具有较强的相关性。结果表明，式(10)可以用于预测圆钢管构件在计算其双参数损伤因子时的组合系数βc。

图7 拟合值与计算值相关性分析

由式(7，10)可计算得到各圆钢管构件达到其极限破坏时的损伤因子值，损伤因子计算值与理论值的比较如图8所示，可以看出损伤因子的计算值与实际值吻合较好，其平均值为1.008，标准差为0.148，方差为0.0219，而利用原始的损伤模型(1)计算出的损伤指数平均值为1.035。由此可见式(7)所示的修正双参数损伤模型可较为准确地反映圆钢管构件破坏时的损伤状态，也验证了所建立的圆钢管构件地震损伤评估模型的正确性。

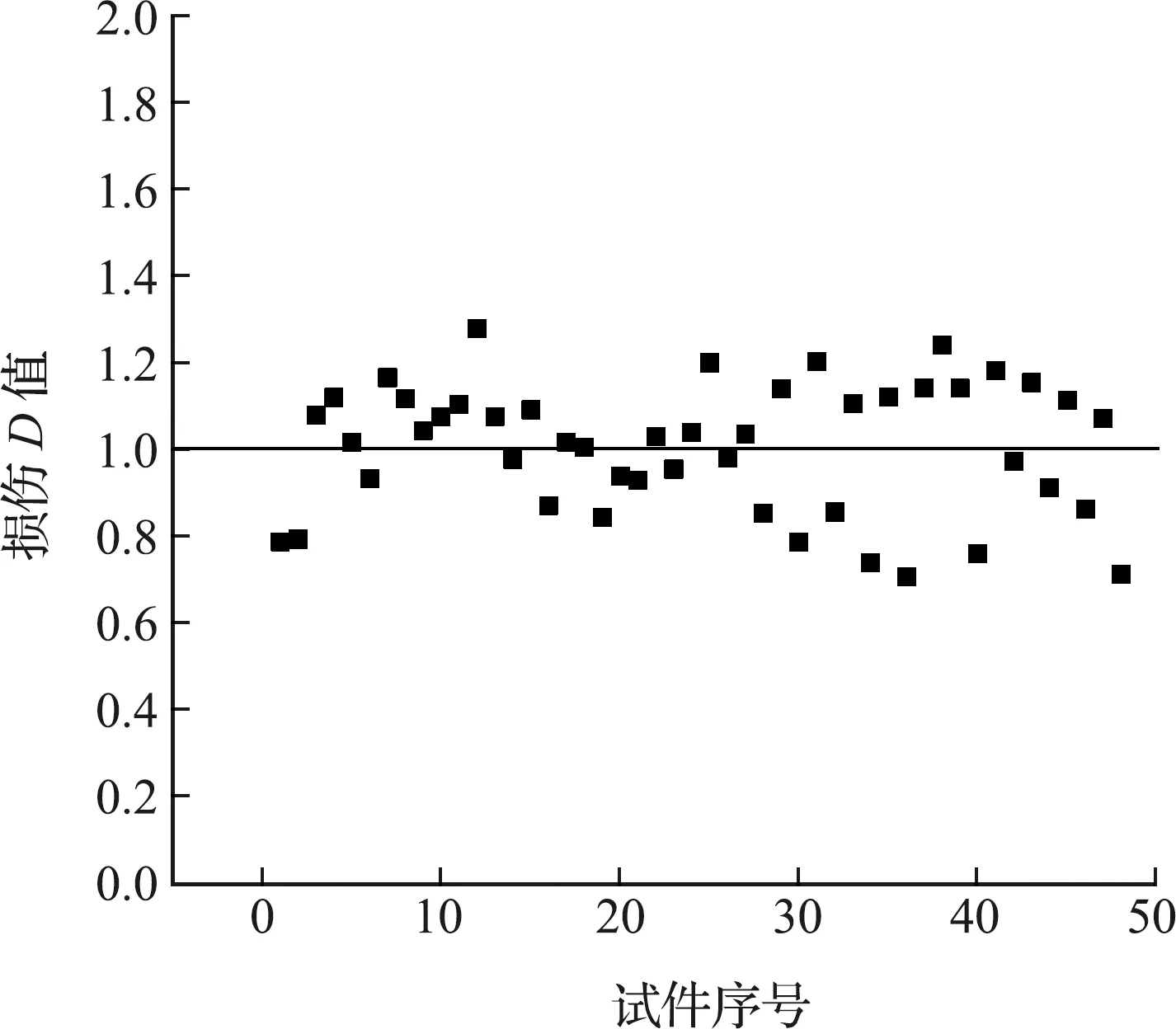
图8 构件破坏时损伤因子D计算结果

4 圆钢管构件性能水准的划分

损伤性能水准定义了建筑物或者结构构件的最低性能指标，作为评定建筑结构和构件破坏状态的标准，其分析对象包括了由整体结构、结构构件、非结构构件以及对建筑功能有影响的场地设施等。根据构件的使用安全性能与损坏程度，建筑钢结构的性态水准可划分为充分运行、运行、基本运行、生命安全和接近倒塌五种情况[26]。分别对应的损伤程度为基本完好、轻微破坏、中等破坏、严重破坏和完全破坏。

参考钢筋混凝土构件的性能水准划分准则，圆钢管构件的性能水准可根据其恢复力特性曲线进行划分，划分关键点界限点包括屈服点、峰值点和极限破坏点等。由式(7)表示的修正Park-Ang损伤模型可得到圆钢管构件在屈服点、峰值点和极限破坏点对应的损伤因子值分别为0.02，0.41和 1.00，以此作为钢管构件性能水准的划分界限值，参考文献[27]中对应的分类标准给出圆钢管构件破坏程度与损伤因子值的界定范围，列入表2，该结果可作为评估圆钢管构件在不同阶段的损伤情况。

表2 破坏程度与损伤因子值范围

各圆钢管构件在屈服点、峰值点和极限破坏点这三个性能水准点处对应的损伤因子值的分布如图9～图11所示。图9表示依据各钢管构件的骨架曲线在构件达到屈服点时由修正后的损伤评估模型得到的损伤因子值，其平均值为0.02，标准差为0.006；图10表示圆钢管构件的骨架曲线其峰值点对应的损伤因子值，平均值为0.41，标准差为0.046；图11表示骨架曲线极限破坏点对应的损伤因子值，其平均值为1.008，标准差为0.148。由此可见构件在屈服点、峰值点和极限破坏点处的损伤因子值标准差均较小，且离散性较小，说明采用该评判准则可较合理地评估钢管构件的损伤破坏程度。

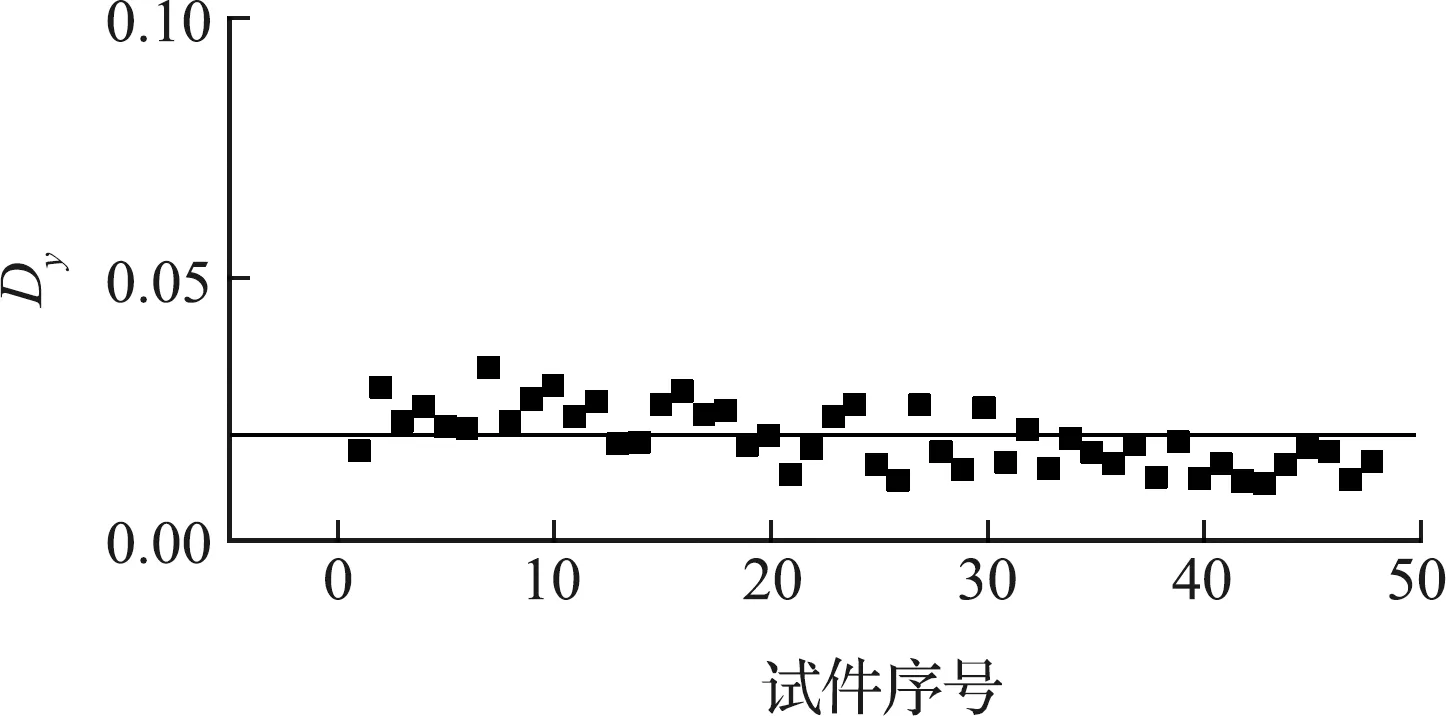
图9 构件屈服点处损伤值分布情况

图10 构件峰值点处损伤值分布情况

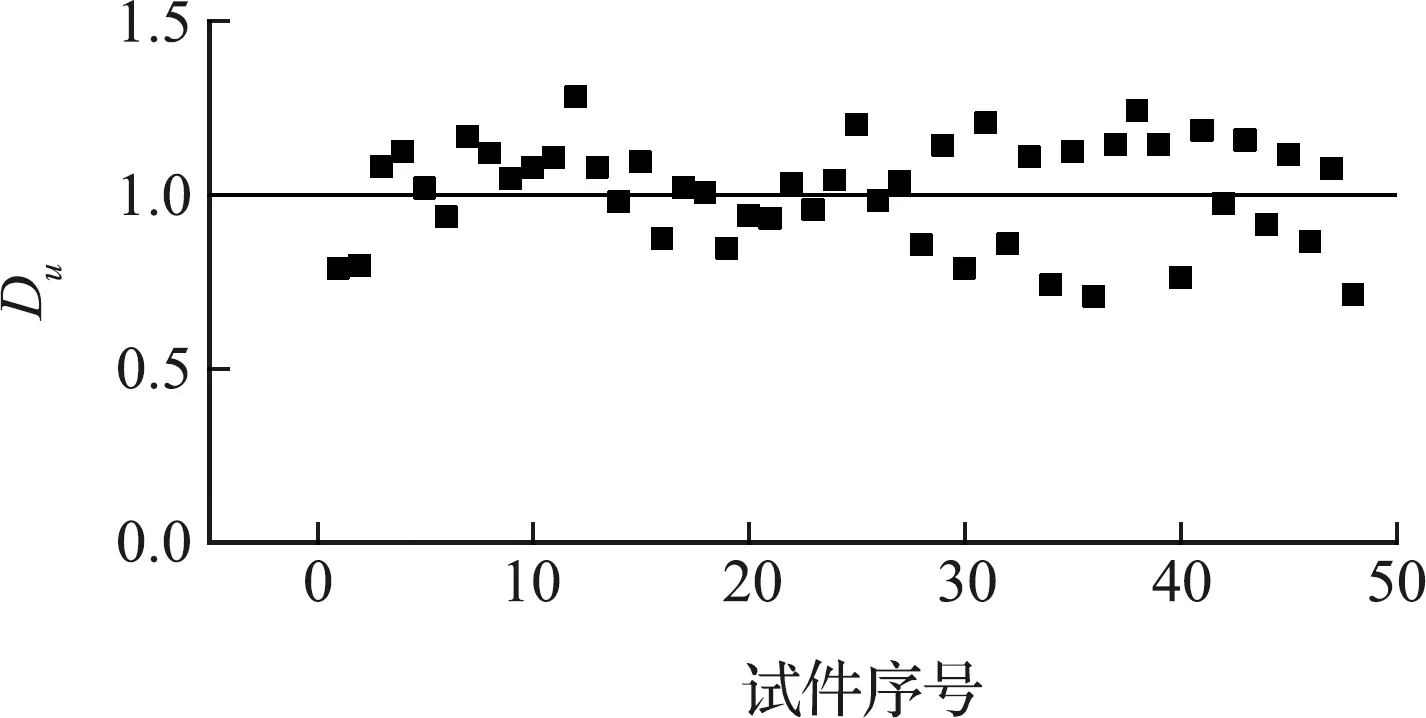
图11 构件极值点处损伤值分布情况

5 结 论

本文基于Park-Ang地震损伤模型，通过修正相关参数建立了适用于圆钢管构件的地震损伤模型。研究了损伤模型组合系数与构件参数间的变化关系，建立了圆钢管构件的双参数损伤判别准则，提出了圆钢管构件在不同破坏状态下的损伤性能水准划分标准。主要结论如下。

(1)利用修正后的Park-Ang双参数地震损伤模型计算得到的圆钢管构件达到其极限破坏状态时的损伤因子接近于1.0，且离散性较小，可准确评估薄壁圆钢管构件的地震损伤状态。

(2)建立了模型组合系数与构件轴压比、径厚比和长细比等参数的关系，可以准确预测构件在不同特征参数下的组合系数值的大小。

(3)根据构件破坏过程，将屈服点、峰值点和极限破坏点作为构件性能水准控制点，其性能水准可划分为基本完好、轻微与中等破坏、严重破坏和完全破坏等四种状态，性能水准对应的损伤因子分别为0.02，0.41和1.00。