弹性地基加肋功能梯度板自由振动分析的无网格法
陈思亚, 陈 卫, 黄钟民, 彭林欣*,2
(1.广西大学 土木建筑工程学院,南宁 530004;2.广西大学 广西防灾减灾与工程安全重点实验室 工程防灾与结构安全教育部重点实验室,南宁 530004)
1 引 言
功能梯度材料FGM(Functionally Graded Materials)作为一种新型复合材料,其组分在空间的连续变化,使其性能也得以连续变化,可以有效缓解应力集中等问题。FGM凭借其优越的力学性能,广泛应用于航天航空和建筑等领域。现已有很多文献基于经典板理论[1,2]、一阶剪切变形板理论[3,4]和高阶剪切板理论[5,6]对功能梯度板自由振动进行了研究。其研究多采用数值解法,如有限单元法[7]、微分求积法[8]和自然单元法[9]等。
对于弹性地基上功能梯度板自由振动问题,国内外也有诸多学者进行了研究。Yang等[10]利用一维微分求积法和伽辽金法求解具有初始应力弹性地基功能梯度板的动力响应。Hosseini-Hashemi等[11]提出中厚功能梯度板自由振动的解析解,并用于分析弹性地基支撑的功能梯度板自由振动。Hasani等[12]基于三阶剪切变形理论,采用解析方法分析弹性地基功能梯度厚板的自由振动。Shahsavari等[13]提出一种新的准三维理论,分析功能梯度多孔板在弹性地基上的固有频率。滕兆春等[14]采用微分变换法研究了弹性地基功能梯度板受压时自由振动和屈曲特性。在研究功能梯度板的问题时,其控制方程除了可以基于几何中面建立,也可以基于物理中面建立。对此,Zhang等[15,16]在此方面做了大量工作,结果表明基于物理中面建立的功能梯度板的控制方程可消除拉弯耦合的影响,具有简化方程的优势。
上述文献很少有涉及弹性地基加肋功能梯度板的研究。文献[17,18]分别研究了弹性地基加肋斜板和变厚度加肋板的自由振动问题。Duc等[19,20]采用伽辽金法和应力函数等方法,在弹性地基加肋功能梯度板结构方面做了一些工作。
本文基于一阶剪切变形理论[21]和物理中面的概念,利用移动最小二乘近似[22]推导近似位移场,通过引入位移协调条件,建立板和肋条节点参数转换关系,分析Winkler弹性地基加肋功能梯度板的自由振动问题。讨论了边界条件和地基系数等对弹性地基加肋功能梯度板自振频率的影响。
2 弹性地基功能梯度肋板无网格模型
2.1 模型描述
如图1所示,功能梯度矩形板由两种材料组成,表面为陶瓷,底面为金属;在全局坐标系(x,y,z)下,矩形板的长宽高分别为a,b和hp,肋条截面的高宽分别为hs和ts。
假定材料常数沿厚度方向遵循如下规律变化
(1)
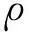
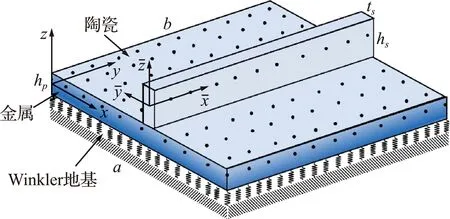
图1 Winkler弹性地基功能梯度加肋板无网格模型

图2 位移协调
功能梯度板与肋条的位移协调如图2所示,z0表示功能梯度板物理中面所在位置,定义为
(2)
2.2 移动最小二乘法近似
由移动最小二乘近似(MLS)[22]求出平板第I个节点的形函数
HI(X)=p(X)TA(X)-1BI(X)
(3)

B(X)=p(XI)ωI(X)
XI和X分别为离散节点和未知点的坐标向量,p(X)为基函数向量,本文基函数均采用二次基,一维p(X)=[1,x,x2]T;二维p(X)=[1,x,y,x2,xy,y2]T;wI为第I个节点的权函数,本文采用如下的三次样条权函数,影响域为圆形影响域。Num表示离散节点数目,板节点取np,肋条节点取ns。
2.3 功能梯度板的能量方程
基于一阶剪切变形理论[21]和物理中面,功能梯度板的位移场可以表示为
(4)
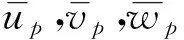
将式(4)表示为基于节点参数的插值,即
(5)
式中
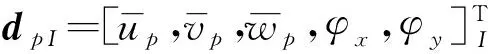
根据几何方程[23],板的面内应变表达为
(6)
(7)
式中微分算子λκ和λγ分别为
功能梯度板的形变势能为
(8)
式中
弹性矩阵Dp和剪切模量G为



由式(5)得板的动能表达为
(9)

假设弹性地基与功能梯度板底部紧密接触,Winkler弹性地基系数为kw,则弹性地基接触势能为
(10)

由式(8~10)得到板的总能量为
(11)
式中Kp=Ku+Kξ
2.4 肋条的能量方程
肋条采用Timoshenko梁理论,在局部坐标下的肋条位移场Vs为
(12)
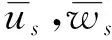
(13)
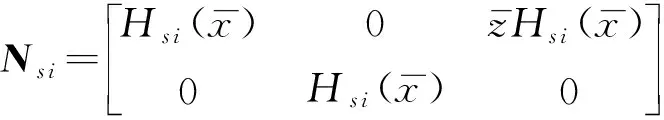

肋条的形变势能为
(14)
式中
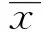
由式(13)得肋条的动能表达为
(15)

由式(14,15)得肋条的总能量为
(16)
2.5 位移协调
如图2所示,肋条的任意离散节点S可在板上找到对应点P(不一定为板的离散节点),肋条与板的位移在接触点C相等,在C点的耦合关系为
(ws)C=(wp)C
(17)
将式(17)由节点位移参数表达为
ds=Tt rdp
(18)
式中
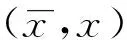
由式(18)可以推导肋条节点参数和板节点参数协调转换矩阵Ts p,详细推导过程可参考文献[24,25]。肋条位置改变只需重新计算转换矩阵Ts p,不必改变板的节点分布。同时将肋条节点位移参数转换为板位移节点参数,不会增加加肋板总体刚度矩阵大小。
2.6 自由振动控制方程
由式(11,16)可以得到整个加肋功能梯度板的总能量为
(19)
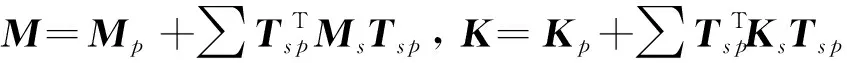

(20)
由式(20)可以推导功能梯度加肋板自由振动问题的特征方程为
(K-ω2M)δp=0
(21)
由于移动最小二乘(MLS)构造的形函数不满足克罗内定理,节点位移参数并不是真实位移。因此,本文采用完全转换法[26]处理本质边界条件。
3 算例分析
通过与有限元以及文献对比验证本文方法的收敛性和有效性。有限元模型功能梯度板采用层合板建模,板和肋条分别采用四节点壳单元(S4R)和梁单元(B31),单元数目分别为10000和100。板节点均匀布置,肋条节点与铺设方向板节点数一致。本文质量矩阵、刚度矩阵以及板厚度方向的积分均采用高斯积分。加肋功能梯度矩形板的边界条件均按x=0,y=0,x=a和y=b的顺序给出,C代表固支,S为简支,F为自由。本文相对误差定义为(λ本文-λ有限元)/λ有限元。
3.1 收敛性以及准确性分析


表1 弹性地基四边简支功能梯度方板的无量纲基础频率λ
3.2 单肋条功能梯度加肋板


图3 y向单肋条功能梯度板无量纲频率收敛性

表2 四边简支n =3的y向单肋条功能梯度板的前五阶无量纲频率λ
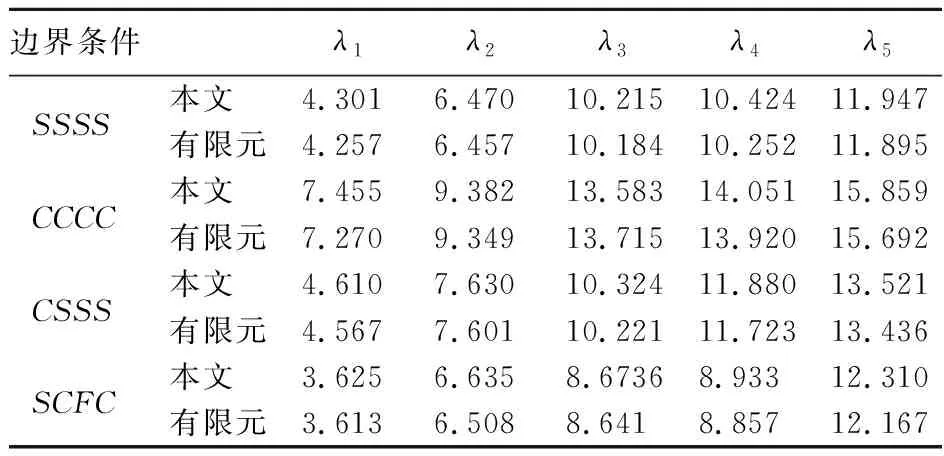
表3 不同边界下n =3的y向单肋条功能梯度板的前五阶无量纲频率λ
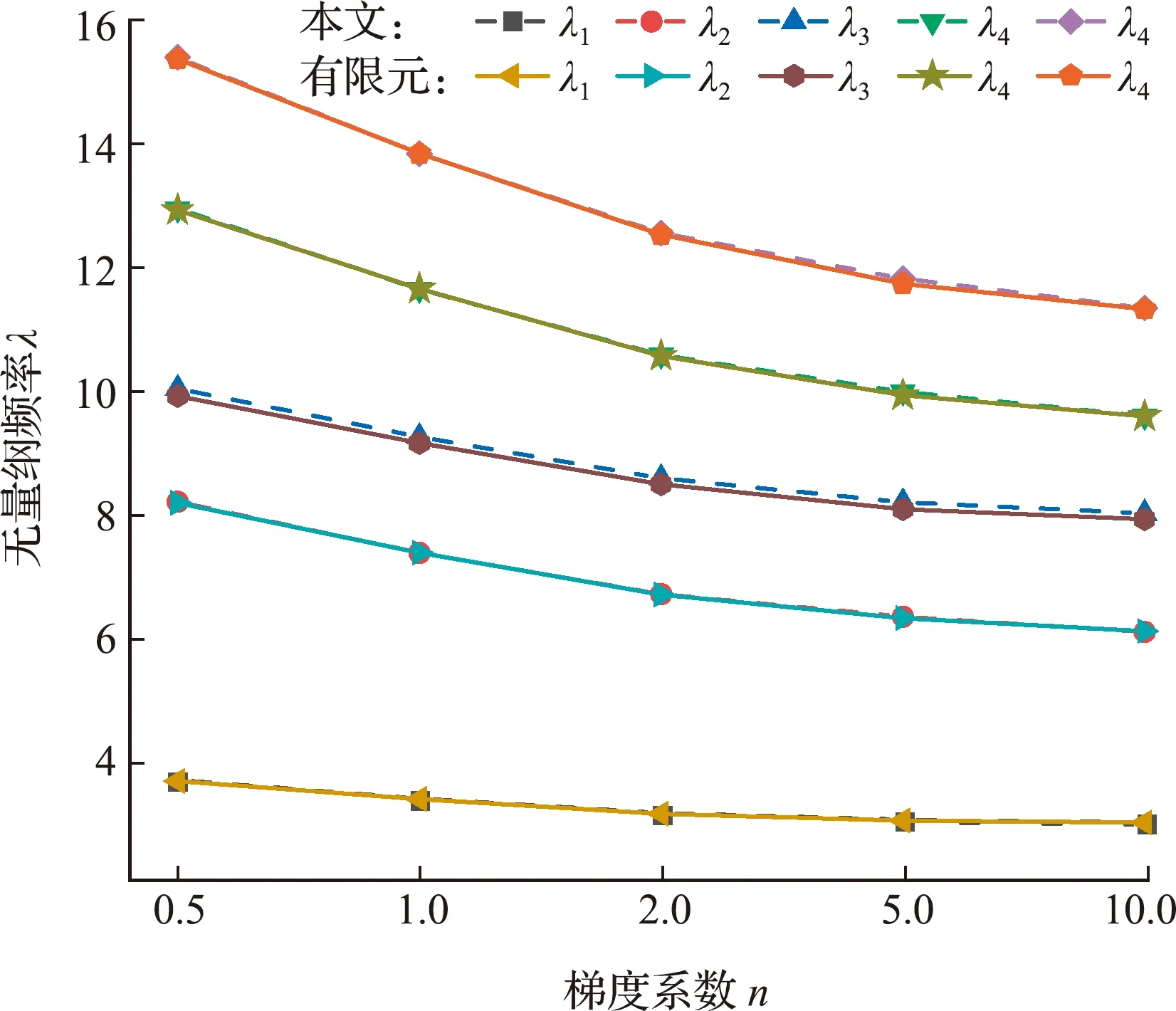
图4 不同梯度系数四边简支y向肋条功能梯度板的前五阶无量纲频率λ

图5 不同梯度系数y向肋条功能梯度板在边界为SCFC下的前五阶无量纲频率λ
在β3=0.05,β4=2时,表4列出了梯度系数为3的四边简支单条中心加肋功能梯度板在不同地基系数下的前五阶固有频率。表5则给出各梯度系数四边简支单条中心加肋功能梯度板的基础频率随着地基参数变化的数值结果。由表4和 表5 可知,随着无量纲地基系数的增加,各阶无量纲频率均有所提高,而基础频率随着梯度系数的增大而降低。
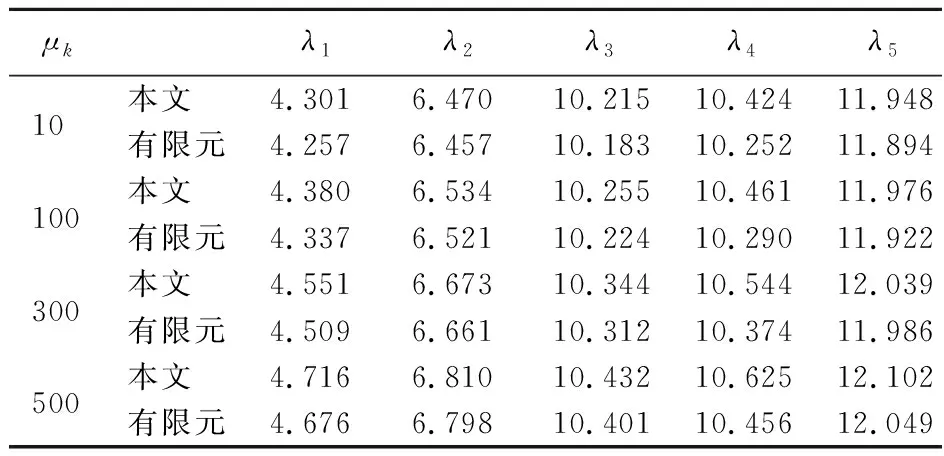
表4 不同地基系数下n =3的y向单肋条功能梯度板前五阶无量纲频率λ

表5 不同地基系数各梯度y向单肋条功能梯度板的无量纲基础频率λ
上述算例均表明,本方法在计算弹性地基加肋功能梯度板的不同边界条件和不同梯度系数等问题时,均具有较高的计算精度,验证了本方法求解这类问题的可靠性。
3.3 多肋条功能梯度加肋板
如图6所示,A型加肋功能梯度板横向和纵向中心各放置一根肋条,而B型加肋功能梯度板则是分别在两个方向等距布置三根肋条。加肋功能梯度板的几何尺寸为β1=1,β2=0.05,β3=0.05,β4=1。
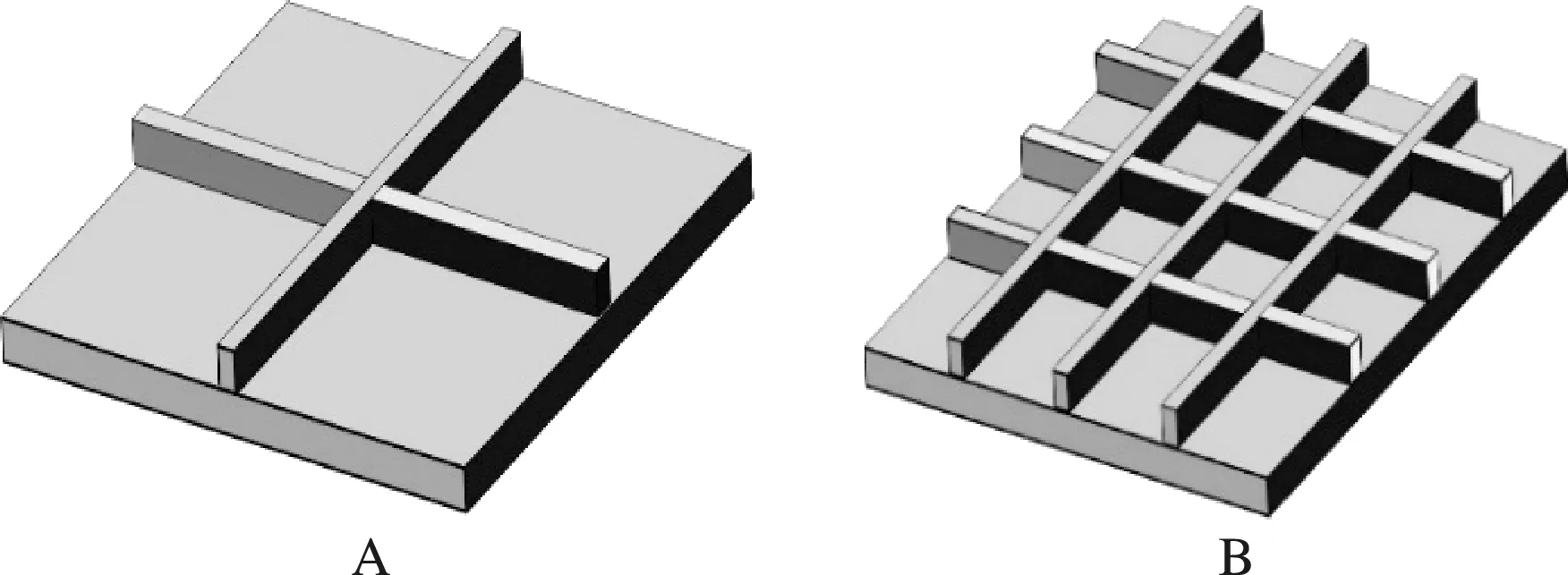
图6 肋条位置


图7 A型加肋功能梯度板无量纲频率收敛性

图8 B型加肋功能梯度板不同边界条件的无量纲基频
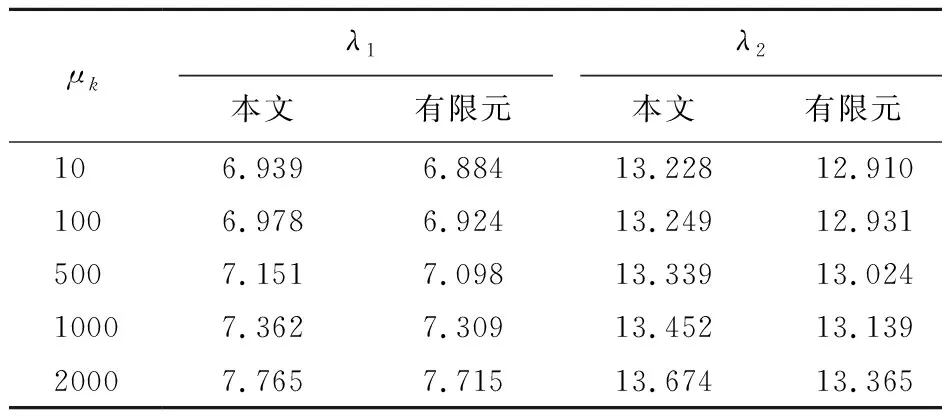
表6 不同地基系数下n =3的四边固支B型加肋功能梯度板前二阶无量纲频率λ

表7 不同地基系数四边简支A型加肋功能梯度板的无量纲自振频率λ
4 结 论
本文基于Winkler弹性地基,采用一阶剪切变形理论和物理中面建立加肋功能梯度板自由振动控制方程,在肋条与板界面引入位移协调条件,将肋条位移转换为板位移,使得本方法在不增加总体刚度矩阵大小的情况下可以计算任意数量肋条的功能梯度加肋板。本方法对于网格没有依赖,肋条位置改变时无需重新布置板的离散节点,仅计算协调矩阵Ts p即可。通过算例的对比验证表明本方法具有良好的收敛性和准确性。对于不同尺寸和数量的肋条的加肋功能梯度板,以及不同地基系数和边界条件下的固有频率求解均有较强适用性。计算结果表明,加肋功能梯度板的固有频率随着边界约束的加强和地基系数的增大而提高。

