重复使用火箭着陆缓冲的机构冲击动力学分析及实验验证

袁晗 王小军 张宏剑,† 牟宇 王檑 王辰

1.北京宇航系统工程研究所, 北京 100076; 2.中国运载火箭技术研究院, 北京 100076;† 通信作者, E-mail: wangxj99@139.com (王小军), zhanghj@pku.edu.cn (张宏剑)

近年来, 诸多国家开展了一子级垂直起降的重复使用火箭相关研究[1], 美国太空探索公司的猎鹰 9 号(Falcon-9)运载火箭和蓝色起源公司的新谢泼德(New Shepard)火箭已经成功地实现火箭一子级的垂直回收和重复使用。火箭的一子级在上升段完成分离后, 通过气动减速和发动机反推减速, 将速度降至较低水平[2]。但是, 由于偏差的存在, 难以控制到零速, 使得火箭必须采用着陆缓冲机构来降低冲击载荷, 提高着陆稳定性[3]。猎鹰 9 号火箭和新谢泼德火箭均采用腿式着陆缓冲机构(简称着陆腿), 其中猎鹰 9 号火箭采用倒三角式着陆腿。垂直起降运载火箭的着陆问题与星球着陆探测器的着陆问题在动力学上具有一定的相似性, 倒三角式着陆腿在 Luna 系列探测器[4]、Surveyor 1月球探测器[5]和 Viking-1 火星探测器[6]等星球着陆探测器中也被广泛采用, 如图1 所示。

图1 倒三角着陆腿的应用Fig.1 Application of inverted triangle landing leg

着陆过程中, 着陆腿产生横向振动, 并导致较大的弯矩, 该弯矩的计算是着陆腿设计的关键。工程上常采用有限元法对着陆过程中的动力学响应进行数值计算[7–8]。有限元法可实现较高的计算精度,但无法得到着陆腿载荷与着陆腿设计参数的解析表达式。在着陆腿构型参数设计阶段, 需要着陆腿参数设计与有限元分析反复迭代, 反复建立不同参数下的有限元模型, 导致设计效率较低, 且参数的影响也不够直观。为提高参数设计效率, 近年来众多学者使用代理模型方法优化着陆腿参数。Yue 等[9]和雷波等[10]利用径向基(radial basis function)代理模型, 对着陆腿可采用的多种缓冲器的参数进行优化。Li 等[11]、王家俊等[12]、吴宏宇等[13]以及刘学翱[14]利用响应面(response surface)代理模型, 对着陆腿的缓冲器参数和构型参数等多个设计参数进行优化。代理模型的精度依赖于样本数量的提高, 样本通常采用数值仿真得到, 故随着优化变量的增多,需要的样本数量和计算量迅速增大。并且, 代理模型通常基于统计得到, 物理意义较不明确, 结果的可解释性较差。

着陆腿在着陆冲击作用下的横向冲击响应问题, 可等效为简支梁在惯性力激励下的横向振动问题。火箭的着陆腿为多节薄壁圆筒结构, 直径沿轴向阶梯变化, 且在节间连接处有端部加强和锁定机构等, 可将其简化为分段等截面和含集中质量的简支梁。针对非均匀简支梁的横向振动问题, 众多学者推导了多种截面变化形式的简支梁横向振动的解析解, 包括含集中质量的等截面简支梁[15–16]、半径随轴向坐标多种幂次变化形式的简支梁[17–18]以及截面沿轴向阶梯变化的简支梁[19]等。上述解析方法均未给出分段等截面和含集中质量的简支梁横向振动的解析解。

面对复杂梁截面形式下梁的横向振动问题时,一般采用假设模态法, 近似地求解振型函数和频率。选取基函数时, 由于非均匀梁横向振动的解析解形式较为复杂, 难以进一步推导半解析解, 故通常采用相同边界条件下 Euler 梁自由振动的振型作为基函数。Cheng 等[20]采用假设模态法建立梁的横向和纵向耦合振动模型, 研究旋转悬臂梁问题中角速度对悬臂梁固有频率的影响。潘旦光等[21]以等截面 Euler 梁的自由振动模态为基函数, 采用假设模态法分析变截面箱型梁振动中的剪力滞效应, 结果表明取前 12 阶基函数时已经具有较高的精度。Kong 等[22]采用假设模态法建立含有两个感应电机的简支梁的横向振动模型, 分析电机参数对系统振动的稳定性的影响。Luo 等[23]采用假设模态法建立弯曲梁的面内和面外振动模型, 并利用该模型研究列车–轨道系统中轨道曲率对系统动特性的影响。

基于上述假设模态法对非均匀梁振动的研究,本文提出一种计算效率高、可解释性强的半解析方法。针对倒三角式着陆腿, 分析着陆过程中着陆腿上的载荷。在轴向, 考虑含缓冲的着陆过程中的静力平衡给出轴向应力, 并给出不同摩擦力方向下的最大轴向应力。在横向, 将着陆过程的激励等效为刚体运动引起的分布惯性力, 通过假设模态法, 近似地求解主腿的振动模态, 利用模态叠加法求解动力学响应, 并考虑横向弯曲变形引起的纵向缩短导致的耦合, 给出横向振动弯矩的半解析计算方法。随后, 通过实验来验证本文提出的计算方法。最后,以满足承载力下着陆腿系统的质量最小为目标, 利用该方法, 分析着陆腿的最优构型, 并进一步分析材料强度对着陆腿最优构型的影响。

1.1 倒三角式着陆腿设计

重复使用火箭采用 4 套倒三角式着陆腿, 每套着陆腿由一条主腿、两条副腿、一个足垫及箭体连接构件等组成。主腿为多节套筒式伸缩设计, 在上升段, 着陆腿处于收拢状态, 紧靠箭体, 在着陆前,着陆腿展开锁定, 实现着陆缓冲的功能, 其构型如图2 所示。左侧着陆腿为收拢状态, 中间和右侧着陆腿为展开状态。主腿、副腿与箭体、足垫均通过球铰相连, 在静力状态下, 主腿、副腿均为轴向受力杆件。主腿共有 4 节, 每节为薄壁圆管, 在收拢状态下, 下方着陆腿套于上方着陆腿内, 展开时套筒逐节展开。主腿的各节间有挡环和锁定机构, 在展开到位后实现两节间的锁定。主腿与足垫相连的节内装有金属蜂窝缓冲器, 在碰撞时, 通过压溃的塑性变形吸收能量, 降低冲击加速度。副腿为等截面薄壁圆管。

图2 倒三角式着陆腿示意图Fig.2 Figure of inverted tripod landing gear

1.2 几何约束

火箭着陆前, 着陆腿已经完成展开锁定, 展开后箭体、主腿、副腿和足垫组成静定结构, 等效力学模型如图3 所示。图3(a)为主腿与箭体轴线构成的平面, 图3(b)为俯视图。设着陆体质量为MB, 箭体上主腿、副腿安装点与箭体轴线的距离分别为rL1和rL2, 着陆腿跨距为xB。设展开后主腿的长度为l1, 主腿与箭体轴线的夹角为β。设副腿的长度为l2, 副腿与箭体的连接点靠近箭体底部, 展开后的支撑高度为h, 主腿、副腿与箭体连接点在y方向的距离为h12, 副腿与箭体轴线的夹角为α, 副腿与图3(a)中x-o-y平面的夹角为γ。为便于分析, 令代表在x-o-y平面内副腿与箭体轴线的夹角。着陆腿上述参数之间的几何约束为

设主腿第i节的长度为l1i, 半径为r1i, 壁厚均为t, 则各节的面积和惯性矩分别为A1i=2 πr1it,Ili=。将主腿各节间的挡环和锁定机构等效为附加集中质量, 如图3 中m11~m13所示, 将缓冲器也等效为附加集中质量, 如图3 中m14所示。设副腿的半径为r2, 壁厚为t, 与主腿相同, 则其截面积为A2= 2πr2t, 截面惯性矩为I2=。

图3 着陆腿几何参数Fig.3 Geometry parameters of landing leg

1.3 着陆过程的刚体运动

火箭着陆时, 足垫首先与地面发生碰撞, 碰撞后足垫与地面保持接触, 主腿和副腿分别绕其与箭体的连接点发生转动, 主腿内的缓冲器压溃, 导致主腿长度缩短, 火箭向下运动, 且火箭质心加速度向上, 直至减速至箭体质心静止。

由于足垫与地面的碰撞无缓冲, 碰撞时间很短,足垫与地面碰撞前后, 着陆腿构型参数变化可以忽略[24–25]。由于缓冲器的作用, 箭体质心加速度为有限值, 故足垫与地面碰撞前后箭体的速度变化同样可忽略。箭体减速下降的过程中, 令v表示箭体的下落速度,v0表示触地时刻的速度, 由于着陆过程箭中体向下运动, 定义v向下为正。分析机构的刚体运动, 并忽略弹性变形, 着陆过程中着陆腿和箭体连接点速度与箭体相同, 着陆腿与足垫连接点的速度与足垫相同, 则l2,rL1,rL2和γ保持不变,l1,xB,,β和h由于刚体运动而发生变化。则由式(1)得副腿角速度、主腿角速度β˙和主腿长度变化率:

令a=-˙代表箭体y方向的加速度, 向上为正,由式(1)和(2)可得足垫与地面保持接触。箭体减速下降的过程中, 副腿的角加速度α˙˙和主腿的角加速度为

着陆过程中, 主腿缓冲器的压溃距离Δl1相对于主腿长度l1较小, 通常有 Δl1/l1＜ 1 0%[10,12–14], 即着陆腿系统的构型变化较小, 故采用式(2)和(3)计算角速度和角加速度时, 忽略角度和β的变化,且近似认为Δl1<>v02/l1。由于着陆过程中火箭做减速运动,v≤v0, 故认为a>>v2/l1,a>>v2/l2, 则角加速度˙和˙可近似为

着陆时, 主腿通过压缩金属蜂窝实现对主腿轴向力的缓冲, 降低箭体的加速度。本文分别分析碰撞过程中的轴向力和横向振动弯矩, 计算着陆过程中载荷着陆腿的最大应力。

2.1 轴向力模型

设T1,T21和T22分别为主腿和两条副腿的轴向力, 为拉力时取正值。N为地面对足垫的支撑力,f为摩擦力, 令μ=f/N为摩擦系数, 其上界为μmax, 即满足 0≤μ≤μmax。在图3 所示的坐标系下, 支撑力N沿y方向, 摩擦力在z-o-x平面内, 设φ∈[-1 80°,180°]为摩擦力与x轴正方向的夹角, 如图4 所示。着陆腿展开后, 箭体、主腿、两条副腿和足垫组成静定结构, 在足垫节点处的静力平衡关系为

图4 静力平衡示意图Fig.4 Diagram of the axle force equilibrium

主腿内装有金属蜂窝缓冲器, 通过金属蜂窝的异面压缩, 降低着陆过程的轴向力。金属蜂窝具有压溃应力稳定的特点[26–27], 则着陆过程中, 主腿轴向力T1<0 可近似为常值, |T1|为金属蜂窝的压溃力,为待设计参数。由式(5)可得支撑力N和副腿 1 的拉力T21分别为

将式(8)的解代入式(7), 可得T21的极大值T2,max和极小值T2,min, 并且T2,max和T2,min均关于μ单调, 即 ∂T2,max/∂μ>0, ∂T2,min/∂μ<0, 故计算副腿的最大拉力T2,max和最大压力-T2,min时, 取μ=μmax。

由于触地前着陆腿的轴向力仅来自着陆腿系统的重力, 故似为 0。着陆过程中, 由于缓冲器的作用, 轴向力近似为定值T, 则着陆腿的轴向加载过程近似为阶跃激励。阶跃激励下, 最大响应不大于 2 倍激励, 即 2T。由于着陆腿在轴向为多节结构,其刚度和振动模态受节间锁定机构的影响较大, 因此参数设计阶段难以对锁定机构准确建模, 导致难以精确地计算其在冲击下的响应, 故在强度设计中考虑最大轴向力为 2T, 该假设将导致应力的计算结果偏大。

2.2 横向振动模型

将着陆过程横向振动的激励考虑为两部分: 1)足垫与地面碰撞前, 着陆腿相对箭体静止, 碰撞后着陆腿在很短时间内发生转动, 引起着陆腿横向振动, 该部分称为“冲击激励”; 2)足垫与地面碰撞后,在着陆腿缓冲器的作用下, 箭体做减速运动, 同时着陆腿的转动过程具有角加速度, 上述刚体运动加速度产生的惯性力引起着陆腿横向振动, 该部分称为“稳态激励”。

本文将着陆腿的横向振动问题等效为简支梁的横向振动问题进行分析。建立单条着陆腿的局部坐标系, 以着陆腿与箭体的连接点为原点, 梁的轴线方向为x轴, 垂直于着陆腿斜向上的方向为y轴, 设着陆腿长度为l, 则着陆腿与足垫的连接点在x=l处。由于着陆腿的截面尺寸沿轴向变化, 设等效简支梁的截面积为A(x), 截面惯性矩为I(x), 材料的密度为ρ, 模量为E。以主腿为例, 考虑附加集中质量后, 上述等效简支梁模型如图5 所示。主腿每段的长度为l1i, 则节间等效质量块的位置坐标为x1j=l11+…+l1j,j= 1~3, 缓冲器等效质量m14的位置为x14=x13+l14,1。由于位于梁端点的集中力不产生弯矩, 故1.2节建立的几何模型中忽略了靠近端点处构件的质量对弯矩的影响。

图5 着陆腿的等效简支梁动力学模型Fig.5 Equivalent beam dynamic model of landing leg

由于副腿为等截面结构且无附加集中质量, 故本文以主腿为例建立横向振动的等效简支梁模型。分析副腿时, 采用主腿的等效简支梁模型, 令附加集中质量为 0,A(x)和I(x)为副腿的截面参数A2和I2,并将着陆腿长度、角速度和角加速度替换为副腿对应的参数。

首先, 建立“冲击激励”的方程。我们认为足垫与地面的碰撞时间很短, 碰撞过程着陆腿横向振动的位移为零, 采用冲量形式描述碰撞过程, 且碰撞过程常规力的冲量可忽略[24–25]。假设足垫与地面的碰撞时刻为t0, 则碰撞过程主腿的角加速度为其中δ()为 Dirac-delta 函数,为足垫与地面碰撞后主腿的角速度, 设触地时箭体下降速度为v0, 由式(2)可得将碰撞过程中着陆腿视为非惯性系, 则碰撞引起的横向惯性力激励见图6。记碰撞引起的惯性力为qc(x):

用MATLAB中newlvq函数建立LVQ神经网络，用newff函数建立BP神经网络，然后根据训练数据利用train函数分别进行训练。LVQ神经网络经过11次训练，用时为3 s，到达误差精度时停止训练，而BP神经网络则是经过16次训练，用时达到6 s后停止训练。由此可见，LVQ神经网络比BP神经网络节省时间。LVQ神经网络误差曲线图如图6所示，BP神经网络误差曲线图如图7所示。

图6 冲击激励的等效模型Fig.6 Equivalent model of the impact excitation caused by the touchdown

然后, 建立“稳态激励”的方程。着陆过程中,火箭质心的加速度为a, 足垫与地面碰撞后到箭体静止的过程中, 主腿的角加速度如式(4)所示, 将着陆过程中着陆腿视为非惯性系, 则质心加速度、角加速度和重力的合力在着陆腿横向的分量记为q1(x):

其中第一项由角加速度引起, 第二项由箭体质心平动和重力引起, 由于缓冲器的作用减速过程中a近似为定值, 由式(4)可得˙正比于a, 故忽略减速过程中sinβ的变化后,q1(x)对于时间可近似为定值。

着陆过程中, 着陆腿所受的横向激励为q(x) =qc(x)+q1(x)。对图5 所示的振动模型, 忽略系统的阻尼, 其横向振动方程为

其中,E为着陆腿材料的弹性模量,I(x)为着陆腿截面的惯性矩。

本文通过模态叠加法求解横向的冲击响应。由于主腿的等效简支梁模型截面非均匀， 且包含集中质量, 其自由振动模态难以解析表达, 故采用假设模态法近似求解横向振动模态, 基函数采用等截面简支梁的自由振动的模态, 第ξ阶为Yξ(x) = sin(ξπxl1)。令Y(x)表示基函数列向量,η(t)表示广义坐标列向量, 则主腿的横向运动表示为

由于系统具有无穷维自由度, 应取n→∞, 但在梁振动问题中, 取少量低阶基函数即可获得精度较高的解[21–22]。本文取n=20。

考虑横向弯曲变形引起的纵向缩短导致的轴向力与横向振动的耦合[28], 令ul代表缩短的长度,ul>0 代表轴向缩短, 当采用式(13)表示y(x,t)时,ul可表示为

将轴向力T考虑为恒定值, 以(t)为广义坐标,则系统动能Ek和势能Ep分别为

其中,Ep考虑了ul导致的耦合项,M和K分别代表广义质量和广义刚度。式中对积分项进行了无量纲化,=x/l1,A0和I0分别代表x=0 处的截面积A(0)和截面惯性矩I(0)。由式(15)和(16)可知,mςξ=mξς,kςξ=kξς, 即矩阵M与K对称。

由式(16)可知, 当轴向力为压力(即T<0)时, 轴向力将降低K的特征值, 即降低系统的刚度。K的最小特征值小于 0 代表存在一个特征向量, 使得随着该向量的模增大, 系统的势能Ep降低, 即着陆腿发生轴压失稳。因此, 若轴向力T< 0, 则假设着陆腿横向振动过程中T始终存在且恒定; 若T> 0, 则假设着陆腿横向振动过程中T= 0。

分布力q(x)在虚位移δ上的虚功为

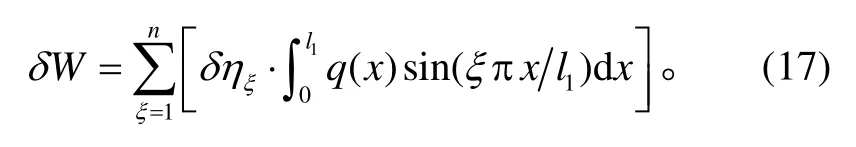
将Ek和Ep和δW代入 Lagrange 方程, 可得η表示的n自由度振动方程:

式中,pη为广义力, 表达式为

可见广义力pη与q(x)线性相关, 令pη,c表示冲击激励qc(x)对应的广义力,pη,1表示稳态激励qc(x)对应的广义力, 则有pη=pη,c+pη,1。pη,c和pη,1的表达式为

当式(18)的右端项为 0 时, 其通解为广义特征值问题(K-ω2M)η0=0。K满足轴压稳定时, 该问题有n个正实数特征值ω12,L,ωn2及其对应的单位特征向量z1,L,zn。令Dω=diag{ω12,L,ωn2},Z={z1,L,zn}, 则M-1KZ=ZDω。进一步, 令Z(t)=Z-1η(t), 并代入式(18), 可得v˙˙+Dωv=(MZ)-1pη,υ与η同为n维广义坐标。令向量pv(0)=(MZ)-1pη(0),pv(1)=(MZ)-1pη(1),则式(18)可解耦为

着陆前着陆腿相对箭体处于静止状态, 故初始状态v=0,˙=0。则由式(22)可得v在碰撞后满足, 其中Ac,ξ和AI,ξ分别表示第ξ阶模态由冲击激励和稳态激励产生的振幅:

则着陆腿横向振动的位移y(x,t)为

对于薄壁圆管, 其弯矩M(x,t)和弯曲应力的大小分别为

式中,E为着陆腿材料的弹性模量;r(x)和I(x)分别为着陆腿截面的半径和惯性矩, 考虑着陆腿的变截面特征后为截面轴向位置x的函数。

2.3 着陆腿的最大应力

我们考虑轴向力和横向弯曲, 给出着陆腿的最大应力计算方法。

主腿需满足轴压稳定, 即广义刚度矩阵K正定。主腿横向振动弯曲应力由式(25)计算, 式中轴向力T=T1,T1由蜂窝压溃强度确定。主腿最大应力的绝对值σ1,max为

副腿的最大应力应考虑轴向力为正和为负两种情况。首先由静力平衡条件(式(6)和(8)), 得到副腿的最大轴向力T2max和最小轴向力T2min。针对轴向力为正的情况, 由于此时轴向力可降低振动弯矩,故计算横向振动时轴向力取 0, 由式(25)得横向振动的最大应力σ2,M,max|T=0。若T2min＜ 0, 应再考虑轴向力为负的情况, 再将轴向力取T2min, 由式(25)得则副腿的最大应力绝对值σ2,max为

3.1 单腿着陆冲击实验

采用单套着陆腿的着陆冲击实验来验证本文提出的计算模型, 实验装置的示意图见图7。采用重量M= 5 吨的模拟箭体, 模拟箭体沿刚性壁面沿高度方向滑动。着陆腿的主腿采用 4 节式伸缩结构,在第 4 节腿内装有铝蜂窝缓冲器, 其直径为 318 mm, 压溃强度为 5 MPa, 则主腿轴力T1= -397 kN。主腿和副腿的材料均为钢材, 材料的模量E=206 GPa, 密度ρ=7800 kg/m3。着陆腿上装有整流罩, 与副腿和足垫连接。由于摩擦系数μ与碰撞过程界面的相对运动有关[29–30], 故针对本文的研究对象难以精确地建模。为降低摩擦建模精度对实验结果的影响, 在足垫与“地面”的接触点下设置滑轨, 近似地取摩擦系数μ=0。

图7 着陆冲击实验装置示意图Fig.7 Device of landing leg impact experiment

着陆腿几何参数: 跨距xB=8.25 m, 支撑高度h=2.8 m, 副腿、主腿安装点与箭体轴线的距离rL1=rL2=1.9 m, 主腿与箭体的夹角β=47.5°, 着陆腿壁厚为t=5 mm。副腿为等截面圆管, 直径为r2=90 mm。将上述几何参数代入几何约束式(1), 得副腿的几何参数α= 67.9°,γ= 10.2°,l2=7.573 m。主腿采用如图5所示的等效模型, 总长度l1=8.614 m, 各段长度l1i、半径r1i、质量块位置x1i和质量块质量m1i如表1 所示, 其中x14和m14为缓冲器。

表1 主腿等效模型的参数Table 1 Parameters of equivalent model of the mean leg

采用高速摄像对触地速度进行测量, 采样频率为 1 kHz。采用动态应变仪测量着陆过程中主腿的应变, 采样频率为 10 kHz。在主腿的第 1 节、第 2节、第 3 节和第 4 节各布置一个测点, 测量轴向应变, 如图7 所示。每个测点中对称地布置 4 片轴线方向的应变片, 在图5 所示的主腿局部坐标系中,4个测点的坐标分别为 1.381, 3.401, 5.421 和 6.753 m, 其中测点 4 位于缓冲器与主腿连接处的下方。进行两次着陆冲击实验, 通过调整下落高度来调整触地 速度。

两次实验中, 由高速摄像测得的触地速度如图8 所示, 图中时间零点为启动摄像机时刻。由图8可见, 实验 1 中触地速度为 1.490 m/s, 实验 2 中触地速度为 2.658 m/s。箭体减速下降过程中, 由于刚性壁面与模拟箭体间存在摩擦力, 导致难以通过支撑力准确地计算箭体加速度, 由式(6)可得支撑力为N=154.9 kN。由图8 可见实验 1 中加速度约为 83.1 m/s2, 实验 2 中为 167.6 m/s2, 说明摩擦力的影响较大。因此, 计算着陆腿的动力学响应时, 实验 1 和实验 2 中加速度a分别取 83.1 和 167.6 m/s2, 并在速度降为 0 后取a= 0, 针对当前各阶模态的位置和速度, 重新计算模态的振幅和相位。

图8 触地速度测量结果Fig.8 Measurement of the touchdown velocity

3.2 理论模型与实验结果的对比分析

首先检验计算角加速度时由式(3)到式(4)的近似是否合理。式(3)中取速度为触地速度v0= 2.658 m/s,α˙˙中 省 略 的 项 cosα/sin3α·v02/l22=0.057 rad/s2,该值显著小于α/l2sinα=11.8 rad/s2;β˙˙中省略项的值为 2.3×10-4rad/s2, 未省略项的值为 9.76 rad/s2。被省略的项均远小于未被省略的项, 说明这种近似是合理的。

由广义速度表示的冲击响应式(23)和角速度的几何约束式(2)可得, 主腿轴压力确定时, 各阶模态的响应Ac,ξ与触地速度成正比,AI,ξ与箭体加速度线性相关。取 20 阶模态坐标, 采用 2.2 节的方法计算主腿前 6 阶模态的频率及在触地速度 1 m/s 下各阶模态的响应, 结果见表2, 其中频率考虑了轴向压力的耦合。由理论值可见 1 阶模态的响应显著高于其他高阶模态, 即振动弯矩主要由 1 阶模态引起。由于 6 阶频率已达到 1 阶频率的 42.7 倍, 在阻尼作用下衰减速度更快, 且响应Ac,6和AI,6均远小于一阶模态的响应Ac,1和AI,1, 故由式(25)计算弯矩和应力时仅考虑前 6 阶模态。

表2 主腿各阶模态频率和单位响应Table 2 Frequency and response for each mode

将测点处的应变数据转化为测点处的弯矩和轴向力, 分别对比实验结果与理论模型计算结果, 对本文提出的计算模型进行验证。由于轴向振动受节间锁定机构的影响较大, 2.1 节中未对轴向冲击的动力学响应进行精确的建模, 故本文在轴向仅对比最大轴向压力, 结果见表3。可见最大轴向力绝对值均未超过|2T1| = 794 kN, 表明 2.1 节的假设是合理的。由于测点 4 位于缓冲器与主腿连接处的下方,故测点 4 处的轴向力较小。

表3 主腿各测点的最大轴向力Table 3 Maximum value of the axle force of each measured section of the main leg

由于考虑高阶模态时阻尼的影响不可忽略, 本文将阻尼考虑为模态阻尼比。在金属材料伸缩式机构的振动问题中, 模态阻尼比取值通常为 0.01~0.09[31–33], 本文取各阶模态阻尼比均为 0.09。通过对实验测量结果进行傅里叶变换, 计算动力学响应的频率, 得到实验 1 中前 3 阶的频率分别为 4.78,19.91 和 44.59 Hz, 实验 2 中前 3 阶频率分别为 4.51,

20.36 和 44.25 Hz。实验测得的频率低于表2 中频率的计算值(约为计算值的 0.523 倍), 原因是实际着陆腿为多节结构, 节间连接降低了着陆腿的横向振动的刚度, 进而降低了频率。4个测点处弯矩的对比结果如图9 所示。为修正频率偏差的影响, 做弯矩–时间曲线时对“计算值”的时间轴进行修正, 修正系数为 1/0.523。图9 中时间零点为碰撞发生时刻, 时间范围为碰撞前 60 ms 至碰撞后 80 ms。最大弯矩的测量值与计算值见表4。

表4 主腿各测点的最大弯矩(kN·m)Table 4 Maximum moment of the measured section (kN·m)

图9 实验测量结果与等效模型计算结果Fig.9 Results of experiments and equivalent model analysis

由图9 可见, 在 4个测量截面, 实验结果与本文方法得到的弯矩变化曲线的趋势较为接近, 但在碰撞开始时刻及弯矩变化较为剧烈的时刻存在一定的差异。表4 显示, 最大弯矩计算值的偏差为 13%,说明本文提出的方法可较精确地计算低阶振动, 但对高阶振动的计算以及对阻尼比的估计存在一定的误差。综合上述分析可知, 计算结果得到的最大弯矩与实验结果相近, 该半解析的理论模型可较准确地计算着陆冲击引起的着陆腿横向振动。

4 着陆缓冲机构参数影响分析

火箭着陆腿的跨距xB由着陆稳定决定[25], 展开后支撑高度h由发动机羽流的流场设计决定[34], 主腿长度和着陆腿的半径为可设计的参数。利用本文提出的理论模型, 通过强度要求计算着陆腿半径,进而确定着陆腿质量, 分析最优主腿长度。由几何约束式(1)可知, 主腿长度l1可由β唯一确定, 故本文分析最优角β。

火箭一级着陆体的质量MB=20 t, 箭体直径为3.35 m。采用 4 套着陆腿, 取xB=8.25 m,h=2.8 m,rL1=rL2= 1.9 m, 则α= 67.9°, 上述参数与 3.1 节实验中采用的着陆腿相同。着陆腿材料采用 LS-3k 0°/90°碳纤维复合材料[35], 模量E= 51.4 GPa, 密度ρ=1600 kg/m3, 抗拉强度为 393.3 MPa, 许可应力取抗拉强度的 70%, 即[σ]= 275.3 MPa, 着陆腿壁厚t= 6 mm, 足垫与地面摩擦系数上限μmax= 0.35, 满足μmax

取触地速度v= 3 m/s, 容许加速度amax= 5 g, 分析着陆腿质量ML,m1,m2与β的关系, 结果如图10所示。可见, 着陆腿质量ML关于角β存在极小值,该构型如下: 主腿与箭体夹角βopt= 41.6°, 第一节主腿半径r11opt= 210.9 mm, 副腿半径r2opt=100.4 mm,主腿设计轴力为T1opt= -527.1 kN, 对应ML的极小值为MLopt=458.6 kg。分析最优构型中主腿的轴压稳定性, 令λk,1(T1)表示主腿刚度矩阵K的最小特征值, 最优构型下λk,1(T1) = 0.272λk,1(0), 临界轴向力T1,cri= -724 kN, 可见此时着陆腿主腿半径由轴压稳定性和横向振动共同决定。

图10 着陆腿质量与夹角β的关系Fig.10 Leg weight under different angle β

提升材料的许可应力[σ]可以降低着陆腿质量,且主腿与箭体的最优夹角βopt也发生改变。下面分析最优构型的着陆腿质量MLopt,βopt与[σ]的关系。假设仅改变[σ], 材料的模量E和密度ρ保持不变如图11 所示, 随[σ]提高,MLopt下降,βopt增大。当[σ]<490 MPa 时, 随[σ]提高,MLopt迅速下降(图11 中虚线左侧); 当[σ]>490 MPa 时, 随[σ]提高,MLopt和βopt的变化均较为缓慢(图11 中虚线右侧)。当[σ]= 490 MPa 和[σ]=800 MPa 时, 最优构型的主腿夹角βopt、主腿质量m1opt、单条副腿质量m2opt、主腿轴向压力T1和主腿轴压失稳的临界轴向压力T1,cri如表5 所示, 可见许可应力由 490 MPa 提升至800 MPa 后, 主腿质量和主腿与箭体夹角变化均较小,副腿质量显著降低。原因在于, 当强度较小时, 主腿截面半径主要由强度决定, 提升[σ]可降低主腿半径, 增大角βopt(即减小主腿长度); 随主腿强度提高,主腿截面半径转而由轴压稳定决定, 此时降低主腿长度将提高主腿轴向压力T1, 进而增大主腿的截面半径, 主腿质量变化不明显。由于副腿的截面半径主要由轴向拉力决定, 故[σ]>490 MPa 时, 提高材料强度仅可降低副腿截面半径, 进而降低副腿质量。由于着陆腿系统的质量主要来自主腿, 故此时提高材料强度总质量变化较小。

图11 着陆腿质量、主腿最优夹角与材料强度曲线Fig.11 Leg weight and optimal angle under different strength

表5 典型材料强度下的最优构型参数Table 5 Configuration parameters of typical strength

5 结论

针对垂直起降重复使用火箭采用的倒三角式着陆腿, 为在着陆腿构型设计阶段准确、快速地计算着陆冲击作用下的振动载荷, 本文提出一种半解析计算方法。在分析着陆冲击导致的横向振动时, 将横向激励等效为足垫与地面碰撞产生的冲击激励和缓冲后刚体运动加速度产生的稳态激励。进一步地, 采用假设模态法建立着陆腿横向振动模态的半解析解, 采用模态叠加法完成着陆冲击作用下系统响应的求解, 并在模型中考虑了轴向力与横向振动的耦合及着陆腿的截面特征。单套着陆腿着陆冲击实验结果表明, 本文提出的方法可较精确地计算着陆过程中着陆腿的弯矩。最后, 基于提出的冲击载荷近似计算方法, 研究了着陆腿构型参数对着陆腿设计的影响, 以着陆腿系统的总质量最小为目标,分析了最优构型, 并进一步讨论了最优构型随着陆腿材料强度的变化规律。