高焓可压缩流动热辐射颗粒两相流理论分析

李婷婷 刘朋欣 袁先旭 周强 李青,†

1.西安交通大学化学工程与技术学院, 西安 710049; 2.空气动力学国家重点实验室, 中国空气动力研究与发展中心, 绵阳 621000; † 通信作者, E-mail: 1201214314@pku.edu.cn

近年来, 航空航天领域的快速发展使得工业界对航空设备的设计要求越来越高。航空航天设备中的流动往往是颗粒两相流[1–5], 传统的单相可压缩流动的理论、计算和实验范式已不能满足当前紧迫的工业需求。此外, 航空航天中的颗粒两相流面临着极端高温环境, 颗粒热辐射效应不能忽略[6–9]。

两相流中的颗粒热辐射效应在航空发动机燃烧室和燃气轮机燃烧室等高温燃烧设备的热动力学过程中占据主导地位, 煤燃烧过程中的颗粒热辐射效应会显著影响颗粒两相流燃烧的热物理过程[10–12]。20 世纪 80年代, Basu 等[13]在考虑颗粒热辐射的前提下, 对气固流化床燃烧过程进行数值模拟, 结果与实验吻合。近年来, Zamansky 等[14–15]对新型太阳能发电项目中的颗粒辐射效应进行系统的研究。新型太阳能发电的基本原理基于气固流化床颗粒热动力学和传热学原理: 流动工质近似于白体, 近似于黑体的颗粒吸收高温热源(太阳)热辐射, 弥散相颗粒与流体通过对流作用发生相间换热, 热流体驱动热机做功发电; 根据热力学第一和第二定律, 做功发电后的流体工质释放热量, 再次被泵运输到辐射对流换热区域, 通过热辐射对流作用, 再次吸收太阳辐射热量, 周而复始的过程见图1。

图1 太阳能发电热辐射颗粒流化床示意图Fig.1 Illustration of radiation- heated particle-laden fluidized bed in particle-received solar energy device

热辐射颗粒会调制湍流拟序结构[16], 从而导致被热辐射效应调制的流体动力学间接地影响颗粒聚团过程, 而颗粒聚团的变化又会反过来调制湍流动力学[17], 这是一个闭环耦合机制。鉴于此, 对于高焓颗粒两相流问题, 必须考虑颗粒热辐射效应。此外, 在极端高温条件下, 颗粒会发生物理化学反应(如燃烧、热解和汽化等)而损失质量, 使得颗粒半径随时间发展而减小, 即缩核效应。缩核效应显著地影响颗粒动力学过程[18–19]。

综上所述, 本研究在不考虑流体相化学反应非平衡效应、电离和激波间断等问题的情况下, 对考虑热辐射效应以及颗粒缩核效应的高焓可压缩颗粒两相流进行理论分析和基本方程推导, 以期为开发高焓可压缩颗粒两相流直接数值模拟工具提供理论依据。

1 极端条件下热辐射颗粒的热响应系数

1.1 极端条件下热辐射颗粒的热力学过程

本文忽略辐射源的类型, 考察一个黑体颗粒在流场中受到热辐射和流体对流换热效应时的热动力学过程。如图2 所示, 颗粒温度为Tp, 高温热辐射源温度为Tr, 环境流体温度为T∞, 假定辐射源温度比环境流体温度高(Tr/T∞>1)。假设流体是完全气体, 不考虑高温电离和激发态等情况, 近似地假设流体为白体, 无法吸收热辐射, 黑体颗粒吸收热辐射增温, 然后通过对流导热作用与颗粒周围流体发生热交换, 颗粒的热力学过程可以用图3 定性地表示, 主要包括与颗粒周围流体的对流换热和辐射吸热两个过程。

图2 热辐射颗粒在流场中热力学过程示意图Fig.2 Schematic of thermal dynamics of radiation heated particle in fluid flow

图3 热辐射颗粒在流场中热量传输路径示意图Fig.3 Schematic of thermal energy transfer pathway of radiation heated particle in fluid

1.2 对流换热的热响应系数

单个圆球颗粒与颗粒周围流体的对流换热过程可用牛顿冷却公式[20–21]表征:

其中,为颗粒热量变化率,dp为颗粒直径,hf为颗粒周围流体对流换热系数,Tp表示圆球颗粒的温度。如果忽略颗粒内部热导效应, 则圆球内部的温度场是各向同性均匀的。还可以表示为

其中,mp表示颗粒质量,Cp,p表示颗粒比热容,t表示时间变量。颗粒 Nusselt 数 Nup表征颗粒对流换热与导热换热效应的比值:

其中,λ∞为流体导热系数。Nusselt数 可以通过数值或物理实验测量获得经验表达式[22]。将式(2)和(3)代入式(1), 可得

在流场中任意Euler点, 对弥散相颗粒采样, 采样单元体积为Vcell, 采样单元内颗粒数为Np, 则颗粒体积分数ϕV为

不失一般性, 给定dp,i为第i个颗粒的直径。为了方程推导的简洁, 采用单粒径假设, 即dp,i=dp, 则采样单元Vcell内Np个颗粒的热量变化率为

将式(5)代入式(6), 可得

将式(8)无量纲化, 取无量纲化标准为

其中, 下角标i表示采样单元内的第i个颗粒, 上角标*表示无量纲物理量, 下角标∞表示流场特征参考量。例如,L∞表示流场特征长度,U∞表示流场特征速度,ρ∞表示流场特征密度。是无量纲颗粒温度,是无量纲颗粒密度,是无量纲颗粒比热容。γ为流体比热比,R为气体常数。将式(9)代入式(8),可得任意采样单元内圆球颗粒群的对流换热无量纲化方程:

根据热对流定义, 采样单元内从颗粒群到流体的热流可以表示为:

本文中令

然后将式(13)代入式(11), 可得

其中,

Stth,pf,i表征第i个颗粒在流体对流换热效应作用下的热响应平衡系数。

颗粒热容响应时间表达式表明, 颗粒密度和比热容越大, 其比热容热平衡响应时间就越大,意味着颗粒越难以被加热到热平衡温度。颗粒对流换热响应时间表达式表明, 第i个颗粒对流换热响应时间是流场特征量 Re·Pr(γ-1)、颗粒粒径/6 和颗粒 Nusselt数 N upi=f( Rep,i,Map,i,Pr)的函数, 即颗粒在高温流动中的对流导热响应时间耦合了流场和颗粒信息。

当 S tth,pf,i→ 0 时, 意味着对流换热的热响应时间比颗粒热容的热平衡响应时间大得多,颗粒温度瞬间达到环境流体的温度; 当 S tth,pf＞＞ 0 时, 意味着比小得多, 颗粒温度达到参考流体的温度是一个非定常过程。

1.3 辐射吸热的热响应系数

类似地, 根据热力学第一定律和 Stefan-Boltzmann 定律[23–24], 在忽略对流和导热作用, 只考虑热辐射作用的情况下, 一个理想的黑体颗粒在真空中的热辐射平衡可表示为

其中,σ∞为 Stefan-Boltzmann 常数,Tr表示辐射源温度。

采样单元Vcell内,Np个颗粒的热量变化率为

将式(5)代入式(18), 可得任意采样单元内圆球颗粒群的辐射换热方程式:

将式(20)无量纲化, 按式(9)的标准, 此处*Tr=由此, 可以得到任意采样单元内第i个圆球颗粒的辐射换热的无量纲关系式:

其中, 流场马赫数Ma=U∞a∞。在完全气体条件下,a∞=为当地音速。

将式(22)代入式(21), 可得

其中,

Stth,pr表征颗粒在高温辐射效应下的热响应平衡系数。

当 S tth,pr→0时, 意味着辐射热响应时间比颗粒热容热平衡响应时间大得多, 颗粒温度瞬间达到辐射热源的温度; 当 S tth,pr>>0时, 意味着比小得多, 颗粒温度达到辐射热源的温度是一个非定常过程。

1.4 颗粒热响应平衡系数之间的关系

含颗粒的高温流动中, 在综合考虑颗粒与流体之间的对流换热作用和热辐射作用的情况下, 任意采样单元内第i个圆球颗粒的无量纲热动力学方程可以表示为式(25), 即含颗粒的高温流动的热平衡方程:

颗粒的辐射热响应平衡系数与对流换热响应平衡系数之间的比值为 S tth,prStth,pf,i= (γR)2hf/σ∞p(γ- 1 ), 体现了颗粒辐射和对流换热响应的快慢。当 S tth,prStth,pf～0时, 即热辐射的响应速度比热对流的响应速度快得多, 在流场中, 颗粒通过热辐射瞬间达到热平衡, 颗粒与流体对流换热作用损失的热量可以忽略, 如图4(a)所示。这种情况下, 不论流场如何变化, 颗粒是等温的, 即颗粒温度Tp*与辐射源的温度相等, 高温颗粒不断通过对流作用单向传热给环境流体。当 S tth,prStth,pf>>1时, 热对流的响应速度比热辐射的响应速度快得多, 在流场中, 颗粒通过热对流瞬间达到热平衡, 颗粒通过热辐射吸收的热量不足以弥补对流换热带走的热量。在这种情况下, 辐射源无法使颗粒温度显著升高,颗粒温度与周围流体温度相当, 如图4(b)所示。

图4 颗粒的辐射热响应系数与对流换热响应系数的比值对热能传递方式的影响Fig.4 Influence of the ratio of thermal radiation response coefficient to thermal convection response coefficient of particles on heat transfer modes

从工程的实际情况出发, 飞行器表面在气动加热作用下发生烧蚀并产生烧蚀颗粒的典型空间高度为 20~30 km, 来流马赫数为 8~20。典型参数范围见表1。通过表1 参数计算得到 S tth,prS tth,pf～O(10-6),因此, 飞行器烧蚀颗粒气固两相流的换热过程是微小烧蚀颗粒离开壁面后, 瞬间被极端高温的辐射源加热到平衡温度, 流体通过对流作用从颗粒带走的热量可以被辐射作用快速弥补, 颗粒始终是恒温的。由上述分析可知, 暂时无需考虑颗粒内部及颗粒与颗粒之间的热辐射。

表1 飞行器常见流场参数范围Table 1 General parameters in aerospace engineering

2 高焓点力模型颗粒两相流方程

2.1 含颗粒的可压缩流动控制方程

本研究考虑的高温颗粒两相流运动方程是可压缩流体动力学方程与基于拉格朗日坐标的弥散颗粒动力学方程的耦合(欧拉–拉格朗日方法)。假设颗粒为数学上无穷小的质点(点力模型), 不考虑颗粒有限体积带来的尾流效应对流场的作用, 则

选取无量纲化标准为

将式(26)无量纲化, 可得

其中, 斯托克斯数St为

其中,ρ*表征流体密度;表征流体微团速度矢量;ρ*表征流体完全气体压力;μ*表征流体动力粘度,ν为流体运动粘性系数;δ表征从 Lagrange 颗粒反馈动量或能量到 Euler 点过程中, 为了保证数值稳定性而采用的光滑函数;ρc*表征在 Lagrange-Euler 插值过程中, 弥散相颗粒群在任意 Euler 点, 即流体采样单元产生的等效密度;Vcell表示颗粒信息采样空间体积;ϕV表示颗粒局部体积浓度;ρp是颗粒密度;ρf是流体密度; St 表征颗粒惯性;τp表征颗粒弛豫时间;τf表征流体特征时间;f(Rep,i, Map,i)是在考虑可压缩效应情况下, 颗粒惯性和颗粒滑移马赫数对斯托克斯数 St 的修正系数[22]; Rep,i为颗粒雷诺数,Map,i为颗粒与流体之间的滑移马赫数。

高温颗粒两相流能量方程是可压缩流体能量方程耦合弥散相颗粒热动力学方程, 颗粒热力学方程主要包含颗粒与流体之间的对流换热效应和热辐射效应:

选取式(29)和=CV(γR Ma2)为无量纲化标准, 将式(32)无量纲化, 可得

其中,

ϕ*表示单位体积流体微团张量粘性做功功率,表示单位体积流体受到的第i个颗粒的相间阻力,表示单位体积流体受热颗粒群通过对流作用传递给流体的热流密度。为了书写简洁, 热流反馈没有采用光滑函数, 这是一种特例, 相当于光滑函数取平均。

式(30)和(33)给出热辐射惯性颗粒在高温可压缩流体中的动力学和热力学方程。弥散颗粒相对动量方程的调制与不可压的情况类似, 能量方程则不同, 马赫数对弥散颗粒相产生的能量扰动产生一个非线性放大效应: 惯性颗粒动量扰动对流体微团做功项热辐射高温颗粒通过热对流作用对流体的单向热流输运γ(γ-1) M a2·。尽管含辐射颗粒的高温可压缩流体热力学过程与太阳能发电工程相同, 但弥散相颗粒对能量输运的影响却不同。太阳能发电工程中的可压缩空气特征马赫数 Ma~0, 意味着能量方程受到的弥散相颗粒诱导是小量γ(γ-1)Ma2~0, 而当前马赫数为 Ma~O(1)-O(10), 即能量方程从弥散颗粒相受到的调制不是小量γ(γ-1)Ma2~O(1) -O(100)。

2.2 碳颗粒化学反应缩核模型

极端高温会使颗粒发生化学反应。以碳颗粒为例, 碳氧发生的化学反应会使颗粒损失质量, 从而导致颗粒大小随时间变化, 见图5。

图5 碳颗粒与氧气完全反应燃烧的示意图Fig.5 Illustration of carbon particle reacts with oxgen

在极端高温条件下, 碳颗粒表面的化学反应速率非常快。因此, 控制反应速率的主要过程是氧气扩散到碳表面的过程。碳颗粒反应和燃烧的速率是非稳态的, 本文假设极高温条件下准稳态过程中碳氧发生完全化学反应。图5 中碳颗粒从初始半径R0缩减到任意t时刻半径R(t), 此过程中任意半径增量Δr所包含的区间内氧气并未参与反应, O2仅在到达半径为R(t)的碳颗粒表面时与碳发生反应并被消耗。R0与R(t)之间任意半径r和r+Δr所包含的空间内 O2摩尔守恒, 即“进 O2速率-出 O2速率+O2生成速率=O2积累速率”[27–29]:

其中,WAr为组分A的摩尔通量, 单位为 mol/(m2·s),组分A表示二氧化碳或者氧气。式(35)两边除以4π Δr并求极限, 可得

根据等摩尔逆流扩散原理(EMCD), 每 1 mol O2扩散到碳颗粒表面并被消耗, 会生成 1 mol CO2, 并向相反方向扩散, 数学表达式为

任意半径r处, 组分A的摩尔通量WAr还可通过有效扩散率De(单位为 m2/s)和A的摩尔浓度CA(单位为 mol/m3)表示:

将式(38)代入式(36), 可得

假设有效扩散率De为常数, 式(38)两边约掉-De, 再进行两次积分, 可得

其中,K1和K2均为积分常数。边界条件: 初始外层气/固界面上,r=R0,CA=CA0;t时刻最新暴露出的气/固界面上,r=R(t),CA=0。因此,

将式(42)对任意半径r求导, 可得

将式(43)代入式(38), 得到组分A的摩尔通量WAr:

由于 1 mol C 参加反应需要消耗 1 mol O2, 并生成1 mol CO2, 因此, 任意t时刻, 半径为R的碳颗粒物质的量的损失率WCR等于r=R处组分A的摩尔通量WAr, 即

碳颗粒的质量损失率为

其中,ρp为碳颗粒的等效密度,Mcarbon为 C 元素的摩尔质量(单位为kg/mol)。

将式(45)代入式(46), 得

选取如下标准:

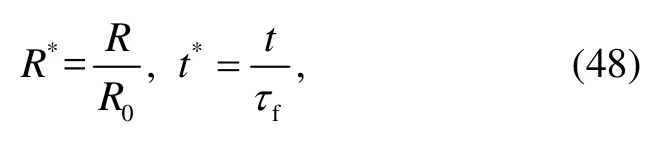
将式(48)代入式(47), 并两边同乘以τf/R0, 进行无量纲化:

令

其中,τchem为化学反应特征时间(单位为 s)。式(49)可转化为

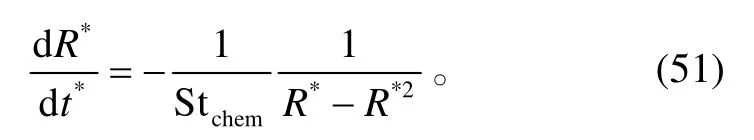
τchem表示碳颗粒化学反应的特征时间, Stchem是碳化学反应时间与流场特征时间的比值, 是表示碳颗粒化学反应的弛豫系数。式(51)给出极端高温下碳颗粒半径随化学反应进行变化的一般规律。

2.3 高温诱导的颗粒非定常惯性效应

如图6 所示, 随着时间增加, 颗粒半径不断减小。由图7 看出, 颗粒粒径变化的速度只与无量纲化的颗粒化学反应的弛豫系数 Stchem相关。Stchem→0 表明颗粒瞬间完成反应, 颗粒质量非定常损失过程相对于流场特征时间是瞬态; Stchem→∞表明颗粒反应非常缓慢, 颗粒质量非定常损失过程相对于流场特征时间是无穷长, 即颗粒粒径不变:

图6 极端高温下颗粒粒径随时间变化的规律Fig.6 Unsteady variation of dimensionless particle radius in function of dimensionless time at extreme high temperature

图7 极端高温下不同缩核效应系数 Stchem 对颗粒粒径-时间变化规律的影响Fig.7 Effect of shrinking core coefficient Stchem on the time evolution of particle radius at extreme high temperature

其中, Rep为颗粒滑移雷诺数, Map为颗粒滑移马赫数,a为当地声速。

式(53)~(55)给出极高温条件下碳颗粒化学反应和流动耦合效应的一般动力学过程。不同的 Stchem无量纲颗粒速度Vp*随无量纲时间t*的变化率如图8所示。可以看出, 弛豫系数 Stchem越小, 颗粒对流体速度的响应越快。这是因为在颗粒损失质量的过程中, 颗粒惯性参数 St 也在不断减小, 颗粒惯性参数St 越小, 颗粒对流体的跟随性越好。在 Stchem→0 极限情况下, 颗粒半径瞬间趋近零, 颗粒速度瞬间达到周围流体速度, 即颗粒减小为示踪粒子[30–31]。

图8 不同缩核效应系数 Stchem对颗粒在均匀流中的非定常速度的影响Fig.8 Effect of shrinking core coefficient Stchem on the time evolution of unsteady velocity of particle from rest to terminal state in an uniform flow

3 结论

本研究针对航空航天背景下的高温颗粒两相流问题, 推导了基于点力颗粒模型的可压缩流体动力学、热动力学分别与热辐射颗粒动力学、热动力学耦合的无量纲方程。

研究结果表明, 与对流导热换热类似, 热辐射对颗粒热动力学的影响是颗粒属性和流体属性的耦合参数, 可表示为热辐射响应系数。针对实际问题的物理量分析结果表明, 热辐射响应系数比对流导热响应系数小几个量级, 意味着颗粒通过热辐射作用瞬间达到高温热辐射源温度, 对流导热换热效应可以忽略不计。可以近似地将颗粒视为等温, 即极端高温条件下, 热辐射颗粒与环境流体的换热过程是单向的, 即等温颗粒不断被环境流体冷却, 通过对流作用传递热量给环境流体。由于热辐射速度太快, 等温颗粒完全无法通过对流导热的冷却作用被降温。在极端高温条件下, 热辐射响应系数与温度的 4 次方成反比, 与马赫数成反比, 导致热辐射响应系数非常小。与此同时, 热辐射颗粒通过对流换热传递给携带相流体的热量会被马赫数平方放大,这是低马赫数颗粒多相流燃烧流化床过程中没有的情况。

本文还考察了颗粒燃烧导致的变质量惯性颗粒效应, 并推导了考虑变质量效应的颗粒动力学一般方程。颗粒燃烧会导致颗粒质量损失, 颗粒粒径变小, 会间接地影响颗粒动力学参数。颗粒动力学参数会影响颗粒动力学过程, 加剧颗粒的非定常性,加快颗粒响应至定常速度的过程。

本研究还推导了无量纲化的可压缩热辐射颗粒两相流耦合方程, 找到影响热辐射颗粒两相流的重要物理控制参数, 为进行多物理条件下的可压缩点力模型颗粒两相流直接数值模拟奠定了理论基础。