基于FPGA的SSD 目标检测硬件加速器设计

谢豪 曹健,† 李普 赵雄波 张兴,†

1.北京大学软件与微电子学院, 北京 102600; 2.北京航天自动控制研究所, 北京 100854;† 通信作者, E-mail: caojian@ss.pku.edu.cn (曹健), zhx@pku.edu.cn (张兴)

计算机视觉是一种使用计算机代替人类视觉系统对图像进行处理的方法, 卷积神经网络(convolution neural network, CNN)是计算机视觉的一种常用方法。随着神经网络算法的不断优化以及计算机系统性能的不断提高, 计算机视觉对日常生活的影响日益扩大, 如自动驾驶路况识别以及 CT 图像识别等[1–2]。一些需要在端侧部署神经网络模型的场景中, 神经网络模型计算量过大, 端侧设备算力不足,功耗受限成为具有挑战性的问题。

常用的目标检测神经网络算法包括 SSD (single shot detector)、YOLO (you only look once)和 R-CNN(region-CNN)[3–5]。SSD 算法检测速度较快, 对尺寸不同的目标均有较好的检测效果。FPGA (field programmable gate array)内部具有大量的并行计算资源, 并且比 GPU 功耗低, 适用于在端侧实现卷积神经网络算法的加速。

FPGA 加速神经网络算法时, FPGA 内部的计算资源的总数是固定的, 应尽可能将计算资源利用起来, 使大部分计算资源处于工作状态。Zhang 等[6]采用卷积分块, 对计算资源进行复用, 采用roofline模型分析来提高计算并行度, 降低系统对数据传输带宽的需求。Ma 等[7–8]采用循环展开的方式实现PE (processing element)单元, 对数据传输和卷积计算建模, 进行设计空间探索, 对不同的模型采用不同的加速器结构, 提高了PE单元的利用率。Gong等[9]利用FPGA的动态可重配置技术, 对同一模型的不同卷积层, 也采用不同的加速器结构, 进一步提高 FPGA 内部资源的利用率。Nguyen 等[10]采用细粒度的层间流水方法, 针对不同卷积层的特点细化资源的使用。

现有的用于目标检测的 FPGA 加速器设计存在一些不足, 比如只有当输入图片的 batch 较大时才能获得比较好的加速性能, 不适合用于嵌入式系统。针对 SSD 算法设计的加速器没有实现空洞卷积(dilated convolution)[11]的算法加速, 而空洞卷积在卷积神经网络中的应用越来越广泛。

本文针对 SSD 网络设计一种加速器, 其优点主要体现在以下几方面: 1) 通过卷积循环内展开的方式, 设计了一种 PE 处理单元, 可以灵活地配置计算并行度, 可用于常规卷积和空洞卷积的加速; 2) 针对 AXI 总线设计了一种数据传输方式, 在不带来额外硬件资源开销的情况下对数据进行重排序, 提高AXI 总线带宽利用率。

1 SSD 目标检测算法

1.1 基础算子

卷积是 SSD 算法中用于提取特征的一种基本算子, 通过卷积核在特征图滑动, 与特征图相乘和相加来完成。对输入特征图(input featuremap, IF)、权重(weights, WT)以及偏置(bias,B)进行卷积的过程如下:

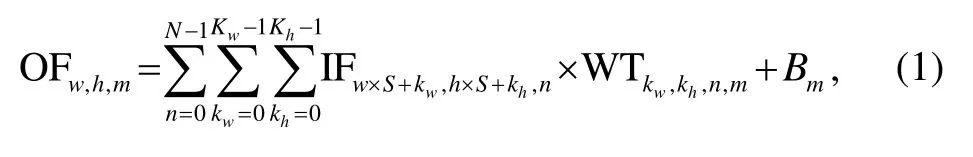
其中, OF 为输出特征图,C为输入特征图宽度,R为高度,N为通道数,W为输出特征图宽度,H为高度,M为通道数,Kw×Kh为权重的尺寸,Kw为宽度,Kh为高度,S为卷积步长。

除上述的标准卷积外, SSD 还使用空洞卷积。图1 是空洞卷积和标准卷积的对比示意图。空洞卷积的计算过程如式(2)所示:

其中,l为空洞率,l=1时空洞卷积与标准卷积一致,其他变量与标准卷积相同。

池化用于降采样, 可以提高模型感受野。常用的池化方法包括最大池化和平均池化。SSD中采用的2×2最大池化计算过程如下:

计算结果需要经过批归一化[12]使得数据分布均匀, 批归一化过程如下:

其中,μm表示均值,σm表示方差,ϵ是为防止σm为0引入的一个小值。每个通道的输出特征图都有各自的μm和σm, 这些参数都是在训练过程中确定的。在推理过程中可以将BN融合进卷积中, 在设计硬件加速器时, 不需要考虑批归一化的硬件实现。

激活函数使用ReLU, 计算方法如下:

1.2 参数量化

训练得到的权重参数一般为浮点类型, 在FPGA中使用浮点数进行乘加计算时消耗资源较多, 计算的延时较多。使用定点数计算可以实现更大的计算吞吐量[13]。Ma 等[14]对 SSD 进行 8 bit 定点化, 精度损失为 0.36%。在 FPGA 中实现神经网络算法时,将参数进行定点化, 用一个Q位的有符号定点数 Fixq来表示小数:

其中, fl 为规定的小数部分长度。

每层的输入特征图、权重和输出特征图分别对应一个 fl, 分别用 flin, flw和 flout表示。fl 的值是通过数据的分布来统计, 应选取适当的 fl 值, 保证大部分的数据都能用定点数 Fixq来表示。输入特征图和权重相乘后需要进行移位, 使得计算结果的 fl 为flout, 移位的位数为

2 硬件设计

2.1 整体架构

如图1 所示, 整个加速器系统是基于 Xilinx 的Zynq 系列的 FPGA 构建, 这一系列的 FPGA 由 PS和 PL 两部分构成。PS 由 ARM 核和外设构成, PL是可编程硬件部分, 由查找表(look up table, LUT)、BRAM (block RAM)、数字信号处理器(digital sig-nal processor, DSP)等逻辑资源构成。PS 端负责调用 PL 端加速器, 实现对整个加速流程的控制以及检测结果显示。PL 端使用 Vivado HLS 语言设计前向推理加速器和后处理加速器, AXI (advanced extensible interface)总线为 PS 和 PL 的通信接口。

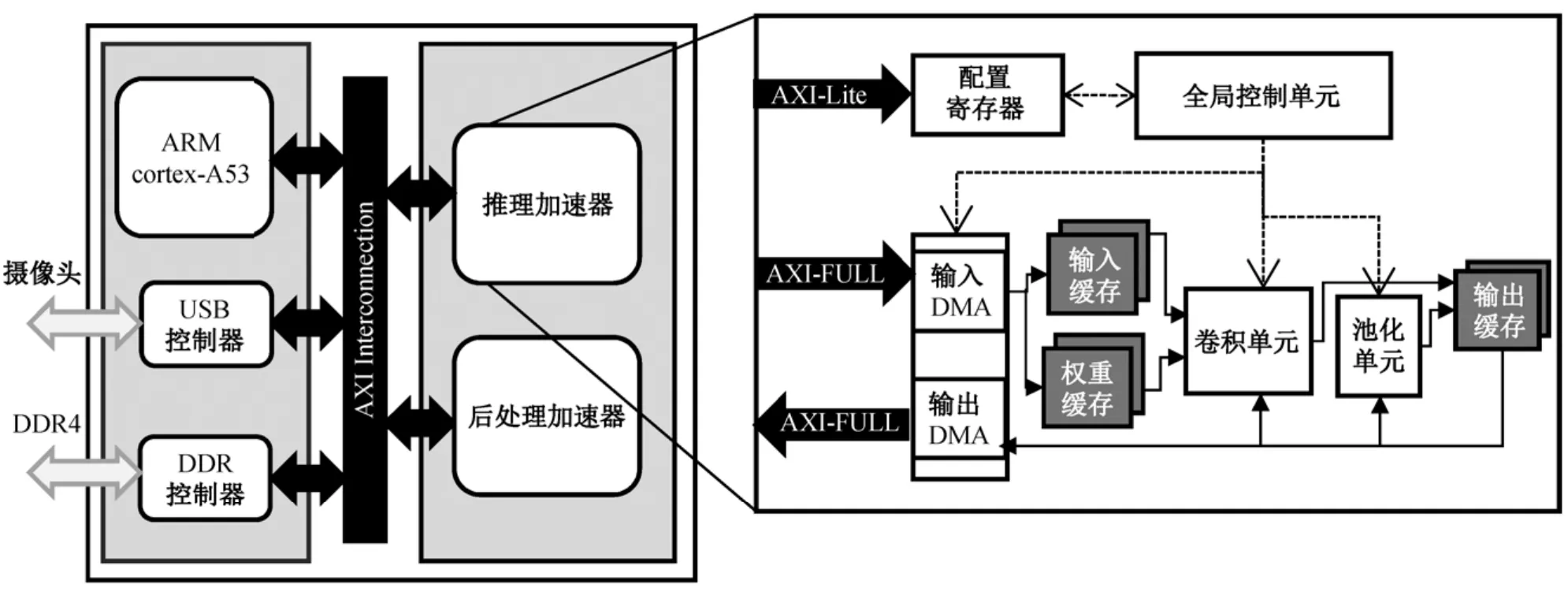
图1 硬件加速器整体结构Fig.1 Overall architecture of hardware accelerator

图1 右侧是前向推理加速器的整体结构框图。加速器由寄存器、全局控制单元、DMA (direct memory access)、片上缓存、卷积计算单元和池化计算单元构成。ARM 通过 AXI-Lite 总线写配置寄存器启动一层卷积/池化的计算, 全局控制器根据寄存器的参数启动各个子模块, 这些参数包括特征图尺寸、输入通道数、输出通道数、卷积核大小和卷积核步长等。全局控制器启动 DMA 进行数据读取,所需数据完成读取后启动卷积模块, 卷积计算完成后再次启动 DMA, 将输出特征图写入 DDR (double data rate)内存中。

2.2 片上缓存

由于 FPGA 内部 BRAM 大小有限, 无法存储所有的权重和特征图, 为了保证加速器能够适用于不同尺度的输入特征图和不同的 FPGA 型号, 本文采用卷积分块的策略对卷积和池化进行计算。为了尽可能减少数据传输的时间, 在片上分别对输入特征图、权重和输出部分使用双缓存进行存储, 这样可以将数据传输的时间隐藏在卷积计算时间中, 使得计算单元的利用率可以趋近于 100%。使用双缓存进行卷积计算的伪代码如图2 所示。

图2 卷积分块以及双缓存计算Fig.2 Convolution blocking and double cache calculation

图2 代码表示一次计算(Tw,Th,Tm)的输出特征图。calculate 函数表示读取输入特征图和权重进行一次卷积计算, 将计算结果写入 Output_buffer 中,memcpy 函数用于将 Output_buffer 中的数据搬运到 DDR 内存中, 在硬件中通过 DMA 实现。由于采用双缓存 Ouptut_buffer0 和 Ouptut_buffer1, 所以在硬件中 calculate 和 memcpy 可以并行实现。

图3中的循环表示通过(Tc,Tr,Tn)分块完成输入特征图和权重的卷积计算, 计算过程也使用双缓存方式将数据传输和计算并行起来。Tr与Th以及Tc与Tw的关系为

图3 分块内部卷积计算Fig.3 Block internal convolution calculation

片上缓存的组织方式如下: 每个输入缓存是一个位宽为Tn×bw(bw 为单个数据的位宽), 深度为Tr×Tc的 RAM,Tn个通道方向的数据合并为一个数据,深度方向上对应(C,R)平面上的数据。以这种方式存储的特征图数据可以灵活地支持各种分块方式,比如 2048 深度 RAM 既可以支持(Tc,Tr)为(40,40)的分块存储, 也可以支持(6, 300)的分块存储。每个权重缓存是由Tm个位宽为Tn×bw的RAM构成,每个RAM的深度为模型所有卷积层中最大的Kw×Kh。与输入缓存类似, 每个输出缓存是一个位宽为Tm×bw, 深度为Tw×Th的 RAM。

2.3 卷积池化模块设计

图4为本文设计的卷积模块结构图。在每个分块的内部, 通过循环展开的方式对卷积并行计算。在输入特征图通道方向和输出特征图通道方向循环展开(图3中最内层的两层循环)。在输入通道方向上的展开次数为Pn(Pn≤Tn), 即一次计算Pn个通道方向上的输入特征图和权重的乘累加(multiplication and accumulation, MAC)。硬件由Pn个乘法器和 ceil(log2(Pn))级加法器树构成, 用流水线的方式进行工作, 因此在一个时钟周期内可以完成Pn个输入特征图和权重的 MAC 计算。上述计算由一个 PE 单元实现, 共有Pm(本文中Pm=Tm)个 PE 单元, 可以并行计算Pm个输出通道的数据。在 FPGA 中乘法由 DSP实现, 共需要Pm×Pn个乘法器。流水线开始工作后,每个时钟周期可以完成 2×Pm×Pn次 MAC 操作, 峰值计算性能为2×Pm×Pn×fGOPS (GIGA operations per second),f为频率。

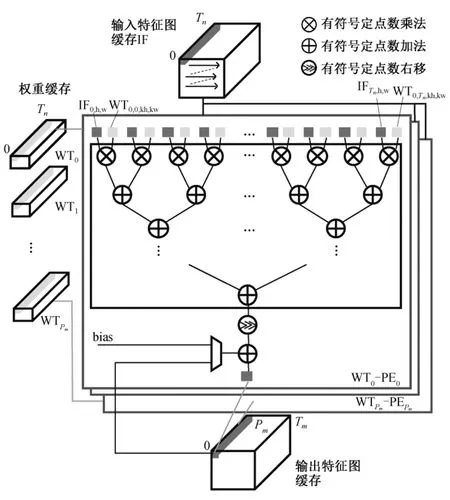
图4 卷积模块Fig.4 Convolution module

每个分块的计算数据流如下: 每个PE单元从各自对应的权重缓存中获取Pn个权重数据, 在之后的每个时钟周期, 权重寄存器中的内容保持不变,输入特征图的数据从缓存中更新Pn个数据到输入寄存器中, 与权重进行MAC计算, 直到计算完一个分块的输出部分。然后将权重寄存器的数据更新为同一个卷积核的下一个权重, 重复该过程, 直到Kw×Kh×Tm×Tn个权重都与输入特征图进行 MAC 计算后, 结束此分块的计算, 切换为下一个分块。在加法树的最后一级, 通过右移单元间计算结果移位进行数据的量化。得到输出数据后, ReLU激活单元根据计算结果的符号位对输出结果进行选择。

基于上述数据流, 本文设计了可以兼容空洞卷积的计算方法。图3 中, 计算常规卷积时, 读取的输入特征图为Input_buffer[ic][S*th+kh][S*tw+kw],空洞卷积读取的输入特征图为 Input_buffer[ic][S*th+l*kh][S*tw+l*kw]。kh和kw为卷积核中每个元素对应的地址偏移, 在权重寄存器数据更新时, 该地址偏移也被更新。实现空洞卷积时, 只需要在片上输入缓存中读数据时加上空洞卷积带来的地址偏移即可。

本文将卷积层和池化层进行融合, 在卷积单元计算出一个输出特征图分块后, 如果卷积层的后一层是池化层而不是卷积层, 则将数据送入池化单元进行最大池化计算, 否则将数据写回DDR内存。与卷积的循环展开类似, 池化单元也采用循环展开的方法对最大池化算法进行加速。池化单元的循环展开次数为Tm, 每一个 PE 的结构如图5 所示。最大池化的过程是用比较器找出池化核中的最大数。以池化2×2为例, 在第一个时钟周期, 从缓存中读取一个数据与最小值(8bit对应–128)做比较, 将比较结果写入寄存器中, 之后将每个时钟周期寄存器中的数据与从缓存读取的数据做比较, 当2×2的数据做完比较后, 将寄存器中的数据写回输出缓存中。

图5 池化模块Fig.5 Pooling module

2.4 可重配置的数据传输方式

本文访问DDR 的方式为通过AXI总线实现。AXI 的传输效率主要与位宽和突发传输有关, AXI的传输带宽与突发传输长度(burst length)以及总线位宽都正相关[15]。本文提出一种数据传输方式, 可以充分利用 AXI 总线提供的带宽, 同时不会带来额外的资源和时间开销。

本文提出的传输方式如图6所示。对于输入特征图, 在通道方向将Tn×bw bit 的数据合并, 向上取整至2n, 不足的部分补零。例如, 当Tn=7, bw=8 且TnTm时, 输入特征图基于Tm通过多组 AXI 总线进行传输。这种数据组织方式可以被重新配置, 以支持任意的Tn和Tn。当输入特征图分块Tc=W时, 启动一次DMA就可以连续传输Tc×Tr个输入特征图数据; 当Tc≠W时, 需要启动Tr次 DMA, 每次连续传输Tc个数据。

图6 数据传输方式示意图Fig.6 Schematic diagram of data transmission pattern

3 加速器部署与测试

利 用 Oxford Hand 数 据 集[16]对 SSD 进 行 训 练 ,得到 mAP (mean average precision)为 0.7820。对训练好的 SSD 模型进行 8 bit 和 16 bit 的量化。将硬件加速器进行部署测试, 构建目标检测系统, 部署平台 为 Xilinx 的 ZCU102 开 发 板 , FPGA 型号 为 Zynq UltraScale+XCZU9EG-2FFVB1156, PS 端软件在Xilinx提供的pynq环境下用python语言编写。对于前向推理加速器, 参数为Pn=Tn=16,Pm=Tm=64,Tw=76,Th=38, 片上输入特征图缓存的深度为4096, 权重缓存深度为 9, 输出特征图缓存深度为 4096。

表1是加速器在不同位宽配置下的加速性能对比。当其他配置都相同时, bw=8 比 bw=16 的利用率下降一半, 与 bw=16 相比, LUT 下降 42%。16 bit 加速器的计算性能为 338.41 GOPS, 8 bit 加速器的计算性能为534.72 GOPS, 位宽降低带来的性能提升为58%。由于 8 bit 加速器对资源的消耗减少, 可以针对时序做出更好的优化, 实现的频率更高。因此,在其他配置相同的情况下, 加速器的位宽越小, 对资源的消耗和对数据传输的带宽需求越小, 实现的最大计算性能越强。

表1 不同位宽下加速器的资源消耗及性能对比Table 1 Comparison of resource usage and performance of accelerator with different bitwidth

图7 展示加速器为 8 bit 位宽时每一层的推理时间以及计算性能。由于从 CONV2_1 到 FC7 这几层的输入输出通道数较多, 在进行卷积计算时能充分利用DSP资源, 所以这几层的计算性能较高, 都大于 440 GOPS。另外, 这几层的大部分时间都用于卷积计算, 数据传输时间能够很好地隐藏在卷积计算时间中, 并且大部分的计算时间都集中在 CONV1_2到FC6之间, 因此实现了较高的整体计算性能。

图7 SSD分层测试Fig.7 Performance of each layer in SSD

从 CONV9_1 到 CONV11_2 的计算性能较低。这几层的计算量较小, 卷积计算时间占比很小, 大部分的时间都用于 PS 与 PL 端的数据交互, 主要是PS通过AXI-Lite总线配置加速寄存器。对于FC7和 CONV8_1 这两层中卷积核尺寸为 1×1 的卷积层,计算性能略低于卷积核尺寸为 3×3 的卷积层, 因为1×1 的卷积计算量较小, MAC 计算的时间少, 但需要读写的特征图数据量较大, 大部分时间用于数据传输。

表2 是本文设计的卷积加速器与其他目标检测加速器在性能和功耗方面的差异。曾成龙等[17]设计的加速器也采用卷积分块的方式进行计算, 但同一个分块的数据在读写时地址不连续, 需要跳跃式读数据。Ma 等[14]设计的加速 SSD 模型实现了 2178 GOPS 的计算性能, 每个 DSP 实现的计算性能为0.499 GOPS, 本文为 0.506 GOPS。Zhang 等[18]在ZCU102 开发板实现对 YOLOv2 的加速, 但是, 由于DSP资源利用率不够, 导致整体计算性能不高。由于使用的模型和部署平台不一致, 本文的设计在推理时间方面不如其他的 SSD 目标检测加速器, 但本文的能耗比为20.96 GOPS/W, 仅次于Ma等[14]的21.78 GOPS/W, 实现了较高的能耗比, 加速器架构效率高。

表2 与其他的FPGA工作比较Table 2 Comparison with other FPGA designs

4 结论

针对 SSD 目标检测算法, 本文基于 FPGA 设计一种硬件加速器, 通过循环展开的方式实现可重配置的计算单元, 利用乘法器和加法树构建了卷积模块, 可实现常规卷积和空洞卷积。本文设计可重配置的数据通路, 用于提高访问 DDR 内存的带宽。将该硬件加速器部署至Xilinx ZCU 102 开发板进行验证, 结果表明, 加速器整体实现 534.72 GOPS 的计算性能。在后续工作中可进行优化, 对加速器进行性能建模, 实现更加合理的资源分配。