表面等离激元波导中表面等离激元二次谐波的产生机制
张同舟 徐艺 高宝伟 张家森
北京大学物理学院现代光学研究所, 北京100871; † 通信作者, E-mail: jszhang@pku.edu.cn
表面等离激元(surface plasmon polaritons, SPPs)是发生在金属表面附近的电子的集体振荡, 因其局域性好和场增强效果显著的特点, 在许多工作中用于增强非线性效应[1–7]。为了在片上光学系统中产生较强的非线性效应, 人们利用能传播 SPP的表面等离激元波导进行了一系列非线性过程研究[8–16],包括二次谐波的产生(second harmonic generation,SHG)、自相位调制和光克尔效应等。在二次谐波产生过程中, 与于传统的介质波导相比, 表面等离激元波导具有尺寸小、场增强效果好的优点, 但也有色散大、损耗大的缺点, 因此转化效率很低[17]。为了消除倍频过程中的相位失配、提高倍频效率,人们设计了多种结构的表面等离激元波导[18–23], 但是尚未见实验成功的报道。
一般来说, 在表面等离激元波导中实现无相位失配的倍频, 需要波导中存在一种基频模式和一种倍频模式, 并且两种模式的等效折射率相等。由于大部分有较大二阶非线性系数的体材料折射率较大, 使得兼具相位匹配、低损耗和低制备难度波导的设计难度很大, 从而给实验的实现带来很大的困难。近年来, 随着材料科学的发展, 基于二维材料(如石墨烯和单层二硫化钼(Monolayer MoS2)等)设计的波导开始应用于产生非线性效应研究中[24–27]。Li 等[28]将单层 MoS2与 Ag 纳米线波导结合, 通过在波导中形成驻波, 实现不受相位匹配条件限制的二次谐波产生。由于驻波场中各点相位相同, 波导中各点产生的倍频光耦合为传播模式时会产生严重的相干相消现象, 其在产生倍频 SPP 时可以利用的波导长度和倍频效率的上限均小于传播的波导模式的倍频。在波导的 SHG 中, 单层 MoS2表现出二阶非线性系数大、对传播模式影响小的特点, 并且兼容成熟的二维材料转移工艺, 使得将基于单层 MoS2的设计和制备用于二次谐波产生的表面等离激元波导时, 可以将相位匹配与非线性材料的安排分开考虑, 难度比使用体材料大大降低。尽管如此, 目前对单层 MoS2在表面等离激元波导中 SHG 特性的研究仍然十分有限。
本文在 SiO2-Ag-MoS2平面表面等离激元波导中实现从基频 SPP 到倍频 SPP 的转化。并且, 进一步的研究表明, 单层 MoS2对表面等离激元波导的传播模式影响很小。这为单层 MoS2在表面等离激元波导中的应用铺平了道路。我们还研究了二维波导中倍频信号的旋转对称性, 信号的 P 分量和 S 分量表现出截然不同的对称性, 揭示了单层 MoS2和Ag 膜之间存在强烈的相互作用。
1 研究方法
为了制备 SiO2-Ag-MoS2平面波导, 我们将一块盖玻片洗净, 然后用热蒸发的方式沉积一层 20 nm 厚的 Ag 膜。在玻璃衬底上用 S 粉末和 Mo 箔作为生长源, 通过低压化学气相沉积(chemical vapor deposition, CVD)的方法, 生长出一些边长约为 100 μm 的 MoS2单晶, 然后将 MoS2单晶用湿法转移到Ag 膜上, 得到所需的波导。
实验装置如图1(a)所示。光源采用钛–蓝宝石飞秒激光器(中心波长为 925 nm, 脉宽约为 150 fs,重复频率为 80 MHz)。入射光先通过一个检偏器,再通过一个半波片, 可以连续改变其偏振。用一个分色镜, 将通过透镜 L1 之后的基频光反射到 100×油浸物镜中, 并允许倍频光通过。通过调节透镜 L1, 改变入射光在物镜后焦面上的光斑大小, 从而控制入射到样品上的基频光的入射角分布范围。分色镜对基频光的反射率很高, 对倍频光的反射率则极低。分色镜置于电动延迟线上, 可以改变入射光斑在物镜后焦面上的位置, 从而改变入射到银膜上的入射角。样品被固定在一个连接在三维电动平移台上的转动台上, 样品表面垂直于物镜的光轴,并可以绕其旋转。我们使用的二维波导, 空气一侧SPP 的漏辐射的中心出射角(简称漏辐射角)为44.59°, 入射角扫描的角度范围设定在漏辐射角附近。L2, L3 和 L4 的焦距相同, L2 与物镜后焦面的距离为焦距f, L2 与 L3 的距离为 2f, L3 与 L4 的距离为3f。样品表面发出的光经过检偏器后被成像到 L2的焦平面 P1 上。空间频谱被成像到 L3 的焦平面 P2 上后, 又成像到与 L4 距离为 2f 的平面 P3 上,被探测器接收。在 P2 处设置光阑, 可以过滤掉空间频谱中不需要的部分。根据实验需求, P3 处的探测器可以选择 CCD 相机(傅里叶成像)、光谱仪(光谱测量)或雪崩二极管(功率测量)。

图1 实验装置示意图、典型的 MoS2 单晶的光学照片和 P3位置的傅里叶图像Fig.1 Diagram of experimental setup, optical photo of a typical single crystal of monolayer MoS2 and Fourier image at P3
2 实验结果与分析
图1(c)展示一个由 CCD 相机在 P3 位置拍摄到的傅里叶图像, 绿色光斑来自照明光, 指示k空间的中心位置, 白色光斑则来源于基频光的反射光,可以看到由自由光到 SPP 转化造成的黑线。在实验中, 基频光从衬底一侧入射到 Ag 膜表面, 并在空气一侧激发传播的 SPP。基频光的 SPP 和隐失场在MoS2上激发倍频光的光场, 而倍频光场再产生传播的 SPP 和自由光场。基频和倍频的 SPP 的漏辐射从衬底一侧射出, 经过物镜收集和后续光路处理后转化为光强信号。
当基频光照射到单层 MoS2上, 且入射角等于漏辐射角时, 可以用光谱仪观测到中心波长为 462.5 nm 的信号光(图2(a)), 且信号光的强度与入射的基频光功率成二次关系(图2(b)), 由此可以确定观测到的信号光是基频光经 SHG 产生的。为了确认倍频光的来源, 我们用只有银膜的部分作为对照, 此时倍频信号可以忽略, 由此确认观测到的倍频光全部来源于 MoS2单晶。

图2 信号光光谱、倍频信号强度与基频光功率和入射角的关系以及基频光和倍频光的傅里叶图像Fig.2 Spectrum observed by the spectrometer, measured SH signal versus power of incidential light and incident angle, Fourier photos of fundamental and harmonic signals
由于隐失场和传播的 SPP 都可以产生倍频光场, 我们进一步研究倍频光的来源。首先测量倍频光强度与入射角的关系, 观察到两个较强的极大值,如图2(c)所示。在 P3 处拍摄的从衬底反射的基频光与出射的倍频光的傅里叶图像(图2(d))。通过时域有限差分(finite-difference time-domain, FDTD)方法, 分别计算不同入射角下入射光场激发隐失场和传播的 SPP 的耦合系数, 然后计算隐失场和 SPP叠加后的光场产生的倍频光场, 再计算出以漏辐射形式辐射到衬底中的倍频光振幅, 最后得到倍频光信号与入射角之间的关系曲线, 与实验数据基本上吻合。图2(c)中 C 点的峰对应的入射角等于漏辐射角,此时基频 SPP 的强度最大; D 点的峰远离漏辐射角,此时基频光的隐失场在波导平面内的波矢分量等于倍频 SPP 的波矢; 再考虑到 FDTD 的计算结果表明基频光 SPP 在 D 点的强度仅有在 C 点的 7.3%, 可以认为 C 点的倍频光主要来源于 SPP 的倍频, 而倍频光强度在 D 点出现第二个极大值则是因为此时基频光场在 SPP 传播方向上的波矢分量与倍频 SPP的波矢相匹配。两个极大值之间的距离由基频与倍频SPP 的相位失配量 Δk决定, 经过拟合得到这一数值为 0.732, 而忽略 MoS2的仿真结果为 0.693, 相差5.6%。由此可知, 在比较粗略的计算中, 可以忽略单层 MoS2对波导色散的影响。
由于入射角与漏辐射角很接近, 直接辐射的倍频光和倍频 SPP 的漏辐射在空间频谱上无法分离,所以无法分别测量二者的强度。考虑到两种成分在干涉特性上的区别, 我们用位置扫描的方法进行更深入的研究。如图3(a)所示, 选择一个单层 MoS2三角片, 将三角片的对称轴、基频光的入射方向和偏振方向置于同一平面内, 通过驱动电动平移台,使基频光沿着三角片的对称轴移动, 同时记录倍频信号的强度和移动的距离。扫描得到的曲线呈现两个明显的峰值和一系列的波动, 这是典型的相干相消造成的波动(图3(b))。
为了计算产生的倍频光转化为 SPP 的比例, 我们建立一个理想模型进行数值计算。由前面的实验可以知道, 相对于 MoS2上产生的倍频光, Ag 膜表面产生的倍频光可以忽略。因此, 我们可以忽略垂直于样品表面的光场分布, 只考察紧贴 MoS2的空气层的光场。假设入射光的照射范围足够大且均匀, 在扫描范围内 SPP 的发散很小, 而入射光斑与 MoS2的形状对倍频光产生的影响可以近似地用位置的实函数来描述, 因此可以忽略在样品表面垂直于 SPP 传播方向上的光场分布, 从而将问题简化至一维。将入射的基频光的振幅作为常量, 首先用FDTD 方法计算隐失场和传播的 SPP 的场强, 然后将二者叠加, 计算出总的基频光光场和各点的倍频光激发强度。各点的倍频光场激发出 SPP 并相干叠加, 同时 SPP 以一定的比例产生漏辐射, 局域的倍频光场也可以直接辐射到衬底中, 与 SPP 的漏辐射叠加后, 被探测器接收。由此, 我们计算得到探测器接收到的倍频信号强度与d的关系曲线(图3(b))。理论曲线的上升沿和下降沿与实验吻合得很好, 而前后两个极大值之间的波动曲线则有一定的差异, 可能是由于实际入射光斑的形状不够规则,使得干涉情况有所不同。在前后两个极大值处,SPP 的漏辐射都在总的倍频信号中占主要部分, 而在中间波动的区域比例较低。

图3 位置扫描示意图以及倍频信号强度与 d的关系Fig.3 Diagram of parameters of position scanning and SH signal vesurs d
根据入射角和入射位置的扫描结果, 当倍频光强度达到最大值时, 倍频光的主要来源是基频 SPP,同时由倍频 SPP 产生的漏辐射占接收到的倍频光的主要部分, 这就意味着存在由基频 SPP 转化为倍频 SPP 的过程。在使用 Krestchmann 结构进行的倍频实验中, 由基频 SPP 产生的倍频光全部以直接辐射的方式传播到衬底中[29]。存在这一差异的原因是我们使用的 MoS2三角片与基频光的照射区域均较小, 因此倍频 SPP 的相干相消效应较弱。如果照射区域的长度无限增大, 则 SPP 的漏辐射在最终信号中的比例可以忽略, 从而与文献[29]的研究结果一致。
根据前面得到的 Δk, 可以计算出波导在倍频时的相干长度为 4.29 μm, 而图3(b)中倍频光强度的上升距离为 22 μm, 远远大于相干长度。这一差异来源于基频 SPP 的强度在d<30 μm 的区域是逐渐增大的, 降低了相位失配造成的影响。当d>26 μm 时,由于基频 SPP 强度上升速率的降低和相位失配量的积累, 倍频光的强度开始下降, 意味着当照射区域的长度L> 26 μm 时, 增加L不会提高倍频光的最大强度。如果改用较厚的 Ag 膜, 则基频与倍频 SPP的漏辐射强度均会降低, 基频 SPP 从 0 增加到最大强度需要的距离增加, 而最大强度会降低。例如,假设 Ag 膜厚度改为 50 nm, 照射区域的长度和单层三角片的边长均足够大, 通过理论计算可以得到:相比于本文中实验的条件, 倍频 SPP 的强度下降为原来的 56.9%, 倍频信号中直接辐射与漏辐射信号的强度比则下降为原来的 34.7%。以上计算结果表明, 可以通过增加 Ag 膜的厚度, 以降低倍频光强度为代价, 换取更纯净的倍频 SPP 信号。
为了进一步探究单层 MoS2在波导中的 SHG 性质, 我们对倍频信号的旋转对称性进行研究。在实验中, 将系统调节至图2(c)的状态, 然后保持基频光的入射角、偏振和入射位置不变, 将样品绕着物镜的光轴旋转, 测量倍频信号的 P 分量和 S 分量与旋转角度的关系, 结果表明, 二者的旋转对称性表现出明显的区别。S 分量的信号呈现出六阶旋转对称性, 与 MoS2三角片的二阶非线性系数的对称性相符[30]。相对地, P 分量的信号呈现出三阶旋转对称性, 有 3个主极大和 3个小瓣。为了解释不同偏振的倍频信号在旋转对称性上的差异, 我们从单层MoS2-Ag 结构的二阶非线性系数出发进行分析。
由于 Ag 的二阶非线性系数远小于单层 MoS2,因此其主要通过自由电子与 MoS2之间的相互作用间接地影响二次谐波的产生。一般地, 单层 MoS2的二阶非线性极化率Pi=χijkEjEk(以下均忽略随时间变化的相位), 其中,χijk代表二阶非线性极化率张量的各个分量,Ej和Ek代表基频光电场强度的相应分量。坐标轴与电场的设定如图4(a)所示。

图4 MoS2 晶胞及坐标轴和电场设定示意图(a)、P 分量的倍频信号与样品旋转角度 φ 的关系(b)以及 S 分量的倍频信号与样品旋转角度 φ 的关系(c)Fig.4 Diagram of a MoS2 cell and axis setup (a), relationship of P-polarized SH signal strength vesurs angle φ (b),relationship of S-polarized SH signal strength vesurs angle φ (c)
当只有单层 MoS2存在时, 由于晶体属于 D3H对称群, 二阶非线性系数张量只有一个独立的非零张量元[29]:χxxx=-χxyy =-χyxy =-χxyx = d1。由此可以得到P分量和S分量倍频光光强与φ的关系:

这一结果表现为六阶旋转对称性, 与玻璃衬底上的MoS2的特性相符。
当单层 MoS2与 Ag 膜接触时, 由于 MoS2与 Ag的自由电子的相互作用, 晶体在z轴方向上的空间反演对称性被破坏, 因此重新对 χ 的各张量元需要进行分析。
设旋转变换

其中,θ=2/3π。由于P对于变换A不变, 则可以得到

设

则得到非线性极化率表达式为

在x′y′z′坐标系中, 基频光场的电场可以写为(E1Pcosφ,E1Psinφ,E1S), 其中EP和ES分别为电场强度的面内和面外分量, 代入式(4), 得到倍频光场的表达式为


将式(5)做坐标变换, 得到

式(6)描述由基频光直接激发的局域倍频光场, 而实验中观测到的是辐射到衬底中的光, 考虑到耦合、干涉和辐射均是线性过程, 可以认为最终观测到的P 光的光场是局域场Ex和Ez的线性组合, 而 S 光完全来源于局域场的Ey。考虑到入射光场不变, 可以得到倍频光 P 分量和 S 分量光强与φ的关系:
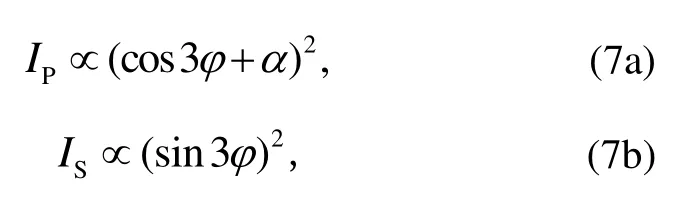
其中,α∈C。如果假定单层 MoS2受 Ag 的影响很小,加入在z方向上的镜面对称条件, 则式(6)中的d2=d3=0,α=0, P 分量退化到六阶旋转对称性的情形。由于发生对称性破缺的 MoS2的二阶非线性系数张量中与z分量有关的张量元难以用理论方法确定, 因此我们结合 FDTD 得到的参数进行拟合计算,结果如图4(b)和(c)所示。可以看到, 计算得到的曲线的旋转对称性和峰值与实验值吻合得非常好, 但是由于测量中的角度精度比较低, 因此存在若干离群点。
通过以上对旋转对称性的分析, 可以得知单层 MoS2与 Ag 膜接触时发生了空间对称性破缺, 因此其二阶非线性系数张量中出现多个新的非零张量元。这一结果为计算单层 MoS2在 SPP 波导中的二阶非线性过程提供了重要依据。
3 结论
本研究在平面表面等离激元波导中实现了从基频 SPP 到倍频 SPP 的转化。由于单层 MoS2与 Ag 膜接触时产生的对称性破缺, 当样品在表面内旋转时,倍频光的 P 分量表现出独特的三阶旋转对称性。对入射光照射位置的扫描结果显示明显的相干相消效应, 意味着相位失配对倍频 SPP 的强度造成较大的影响。如果要提升基频 SPP 到倍频 SPP 的转化效率, 就需要利用特别设计的波导或者准相位匹配的方式来降低相位失配的影响。与 BBO 和铌酸锂等非线性体材料相比, 单层 MoS2对表面等离激元波导模式的影响极小, 且兼容成熟的二维材料转移方法, 因此在设计用于二次谐波产生的表面等离激元波导时, 兼顾相位匹配、损耗和制备可行性的难度大大降低, 还可以借助光刻方法制备周期性结构,实现准相位匹配。如果进一步的研究中能够在波导中实现较高效率的表面等离激元倍频, 就可以为光子芯片中的相干光源和参量过程提供一种新的实现方法。

