独辟蹊径优解三道高考题
孙 琳
(江苏省南京市金陵中学河西分校 210000)
在高考二轮复习中,研究高考真题是“规定动作”,其重要性不言而喻.高考真题如同一坛老酒,越品越醇,愈久弥香.每次研究都有新的发现,发现她的蕴味,发现她的内涵,发现她的独特魅力——不同层次的学生有不同的解法,以致单位时间内创造不同的价值(分数).
1 逆向思维出奇招
文献[1]提到李白买酒与逆向思维的趣事:李白无事街上走,提壸去买酒.遇店加一倍, 见花喝一斗.三遇店和花, 喝光壸中酒.试问酒壶中,原有多少酒?
不同年龄段的学生有不同的方法,如果学过方程,首先想到这是一个关于一元一次方程的问题, 设壸中原有酒x斗,第一次遇到酒店后壶中有酒2x斗,遇到花后壶中有酒(2x-1)斗,第二次遇到酒店后壶中有酒2(2x-1)斗,遇到花后壶中有酒[2(2x-1)-1]斗,第三次遇到酒店后壶中有酒2[2(2x-1)-1]斗,遇到花后壶中有酒{2[2(2x-1)-1]-1}斗.

这种做法有点麻烦,若反过来考虑, 问题就简单多了,并且用不到方程,下面我们用逆推法求出壶中原有多少酒:

第三次遇花之后第三次遇花之前第三次遇店之前第二次遇花之前第二次遇店之前第一次遇花之前第一次遇店之前壶中有酒(斗)00+1=11÷2=1212+1=3232÷2=3434+1=7474÷2=78
逆向思维用到下面这道高考题中再也恰当不过.
例1 (2019年浙江省数学高考第21题)如图1,已知点F(1,0)为抛物线y2=2px(p>0)的焦点,过点F的直线交抛物线于A,B两点,点C在抛物线上,使得△ABC的重心G在x轴上,直线AC交x轴于点Q,且点Q在点F的右侧.记△AFG,△CQG的面积分别为S1,S2.

图1
(1)求p的值及抛物线的标准方程;

解法1(官方提供的标准答案,笔者略有添加)


求面积比,最后几步看似简单,实则不然,倒数第二步省略不少运算过程.
再令m=t2-2,则m>0,

由于题目的“忽悠”,顺向思维设直线AB方程再正常不过了,后果是运算量大得无法做或不敢做下去,因为AC是题设中最后出现的,所以常规思维是将其作为最后考虑的条件,但运用李白买酒的逆向思维,如果设AC方程有意想不到的方便.

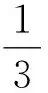
2 选择地形建系
用坐标法求解立体几何大题是考生在考试时的首选方法,即通过坐标运算代替了运用空间想象的纯几何证明.
例2 (2020年浙江数学高考题第19题)如图2,三棱台DEF-ABC中,平面ADFC⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(1)证明:EF⊥DB;
(2)求DF与平面DBC所成角的正弦值.
为了追求效益最大化,也是最为保险,一般学生都会用建系坐标法,平时学生建系方法用得非常溜,官方提供的建系解法,中规中矩,不再呈现,笔者提供下面别解短小精悍,令人耳目一新:

图2 图3




没有繁杂的运算,没有诡异的思路,短短几行就解决了当年“卡住”不知多少考生的难题.
3 数形结合省笔墨
数形结合的应用大致又可分为两种情形:借助于数的精确性来阐明形的某些属性,或者借助形的几何直观性来阐明数之间某种关系.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”使复杂问题简单化,抽象问题具体化,从而实现优化解题途径的目的.
例3(2015年浙江省数学高考理科第18题)设函数f(x)=x2+ax+b(a,b∈R),记M(a,b)是|f(x)|在[-1,1]上的最大值.

图4
(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a,b满足M(a,b)≤2时, 求|a|+|b|的最大值.
分析官方提供的答案在代数运算方面发挥极大优势,转化为二次函数在单调区间上取最值问题,充分挖掘对称轴隐含条件(略),下面方法1充分利用图象直观功能.
解析(1)由已知得|f(x)|≤M(a,b)=M,去掉绝对值有-M≤x2+ax+b≤M.
即-x2-M≤ax+b≤-x2+M.
记f1(x)=-x2-M,f2(x)=ax+b,f3(x)=-x2+M,如图4,在x∈[-1,1]上,函数f2(x2)=ax+b被夹逼在抛物线f1(x)和f3(x)之间.
因为斜率a的正负性不知道,所以写成绝对值形式:-|a|+b≤f2(x)≤|a|+b.
根据图象有-1-M≤-|a|+b.
即1+M≥|a|-b,-1+M≥|a|+b.
两式相加,得2M≥2|a|.故M≥|a|≥2成立.


