也谈“奔驰定理”及其空间形式的推广证法

魏东升

(福建省厦门双十中学漳州校区 363107)

文[1]从三角形面积和线段比例关系、正弦形式的三角形面积公式、三角形重心的性质、向量按垂直坐标系分解的性质和平面向量基本定理等五个方面对奔驰定理进行了证明，读来受益匪浅．笔者对该定理也进行了进一步的探究，并在文[1]的基础上又得到了五种方法，同时对其空间形式的推广也给出了三种证法，为方便讨论，引该定理如下：

图1 图2

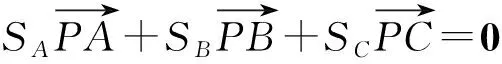
如图2，延长AP交BC于点D，可得

所以只需证明等式

因为B,C,D三点共线，所以上式显然成立.

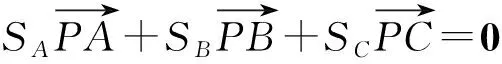
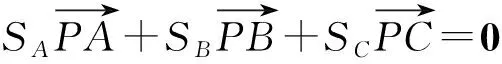
图3

以点P为原点，PC所在直线为x轴，建立如图3所示的直角坐标系，记PB和PC的夹角为θ1，PC和PA的夹角为θ2，PA和PB的夹角为θ3，不妨认为A,B两点分别在一，四象限，其他情况同理.

证法4 结合题意可知a，b，c三数同号.

所以SA∶SC=a∶c=a∶c.

同理可证SB∶SC=b∶c，SA∶SB=a∶b.

即SA∶SB∶SC=a∶b∶c，定理得证.

由克拉姆法则可知

=SA∶SB=a∶b.

同理可证SB∶SC=b∶c，SA∶SB=a∶b.

即SA∶SB∶SC=a∶b∶c，定理得证．

“奔驰定理”有多种推广形式，如可把点P由三角形内任一点推广到三角形外任一点，进而推广到空间中三棱锥内的任一点．以下给出该定理的空间推广形式及相应的证明方法:

图4

即只需证明等式

如图4，延长AP交平面BCD于点E，则

因为B，C，D，E四点共面，所以上式显然成立，定理得证.

所以VA∶VD=a∶d=a∶d.

同理可证VA∶VB=a∶b，VA∶VC=a∶c，VA∶VD=a∶d.

即VA∶VB∶VC∶VD=a∶b∶c∶d，定理得证.

由克拉姆法则可知:

同理可得

所以a∶b

=VA∶VB=a∶b.

同理可证VA∶VC=a∶c，VA∶VD=a∶d.

即VA∶VB∶VC∶VD=a∶b∶c∶d，定理得证.