基于素养导向和能力立意的高考数学备考策略——2017-2021年全国卷中解析几何解答题分类综述

巨小鹏

(陕西省汉中市龙岗学校 723102)

平面解析几何是选择性必修主题二几何与代数的内容，是创立微积分的基础.其方法就是通过建系，借助直线、圆与圆锥曲线的几何特征，导出相应方程，再用代数的方法研究其几何性质，完美体现了数形结合思想.学生在学习过程中往往有这样的几个难点：一是对基本概念和基本公式理解不够深刻；二是对解析几何中所要用到的思想和方法掌握不够；三是代数运算能力不够.针对这些难点，依据新课程标准，理解基本概念，依托高考真题，总结规律，掌握方法，把握其内在逻辑，优化计算方法.

1 精准领会新课程标准要求

1.1 新旧课程标准教学要求区别

新课标删除了“体会斜截式与一次函数的关系”，明确了“掌握平面上两点的距离公式”，增加了能解决一些“实际问题”.对知识内容的整合，用代数法研究几何问题，体现数形结合思想是本章内容的核心，这种思想贯穿该内容教学的始终.新课标对抛物线的要求是了解，难度也有所降低；旧课标“能用坐标法解决一些与圆锥曲线有关的简单几何问题(直线与圆锥曲线的位置关系)和实际问题”降为“了解椭圆和抛物线的简单应用”，增加了“平面解析几何的形成与发展”，引导学生感悟数学的文化价值.删除了“曲线与方程”相关内容.

1.2 四了解、四探索和四能

了解：了解圆锥曲线的实际背景；了解抛物线与双曲线的定义、几何图形和标准方程，以及它们的简单几何性质；了解抛物线与双曲线的定义、几何图形和标准方程，以及它们的简单几何性质；了解椭圆、抛物线的简单应用.

探索：探索确定直线位置的几何要素；探索并掌握直线方程的几种形式(点斜式，两点式及一般式)；探索并掌握平面上两点间的距离公式，点到直线的距离公式；探索并掌握圆的标准方程与一般方程.

能：能根据斜率判定两条直线平行或垂直；用解方程组的方法求两条直线的交点坐标；根据给定直线、圆的方程，判断直线与圆，圆与圆的位置关系；能用直线和圆的方程解决一些简单的数学问题与实际问题.

重点提升学生直观想象、数学运算、数学建模、逻辑推理和数学抽象素养.

1.3 高考考情统计分析

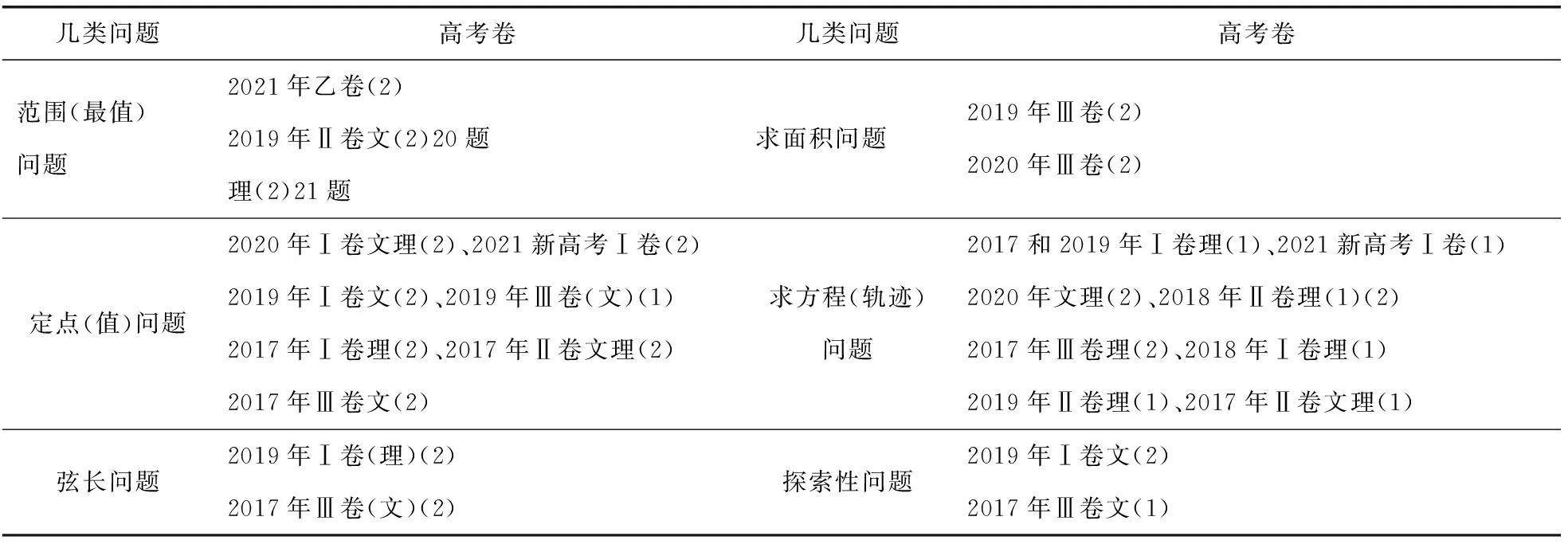
几类问题高考卷几类问题高考卷范围(最值)问题2021年乙卷(2)2019年Ⅱ卷文(2)20题理(2)21题求面积问题2019年Ⅲ卷(2)2020年Ⅲ卷(2)定点(值)问题2020年Ⅰ卷文理(2)、2021新高考Ⅰ卷(2)2019年Ⅰ卷文(2)、2019年Ⅲ卷(文)(1)2017年Ⅰ卷理(2)、2017年Ⅱ卷文理(2)2017年Ⅲ卷文(2)求方程(轨迹)问题2017和2019年Ⅰ卷理(1)、2021新高考Ⅰ卷(1)2020年文理(2)、2018年Ⅱ卷理(1)(2)2017年Ⅲ卷理(2)、2018年Ⅰ卷理(1)2019年Ⅱ卷理(1)、2017年Ⅱ卷文理(1)弦长问题2019年Ⅰ卷(理)(2)2017年Ⅲ卷(文)(2)探索性问题2019年Ⅰ卷文(2)2017年Ⅲ卷文(1)

从统计明显看出：(1)解答题第一问考查轨迹方程比较多，难度不大，考查基础概念，基本方法；(2)定点(值)问题也是第二问常考类型，然后是范围(最值)问题，其中可能与函数最值或者不等式交汇考查；(3)探索性问题也值得关注，试题本身的开放性只有在探索中才能体现出学生思维的方向性，作为选拔性考试，难度稍大.

2 几个常见问题多视角通法分析

2.1 解决范围(最值)问题中的多个视角

求范围(最值)问题常常将目标转化至函数或者不等关系，此时审视角度较多，比如利用几何特征数形结合、判别式、求值域(二次函数和求导函数法较多)、基本不等式、正余弦定理、三角换元(参数方程法较多)、利用题中隐含条件建立不等关系或者利用线性规划及其综合方法解决问题.

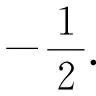
(1)求C的方程，并说明C是什么曲线；

(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为点E，连接QE并延长交C于点G.

(ⅰ)证明：△PQG是直角三角形；

(ⅱ)求△PQG面积的最大值.

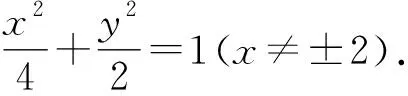
(2)(ⅰ)设直线PQ的方程为y=kx,可知k>0,直线PQ的方程与椭圆方程x2+2y2=4联立.

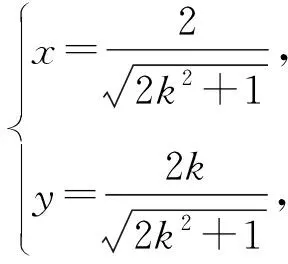
因为点P在第一象限，所以

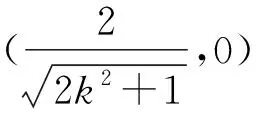
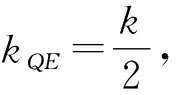
消去y，得

①

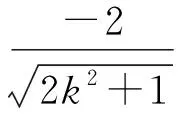
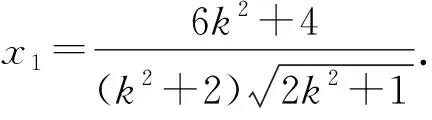
代入直线QE方程中，得

所以点G的坐标为

直线PG的斜率为

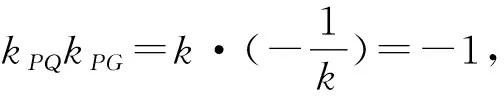
所以PQ⊥PG.

因此△PQG是直角三角形.

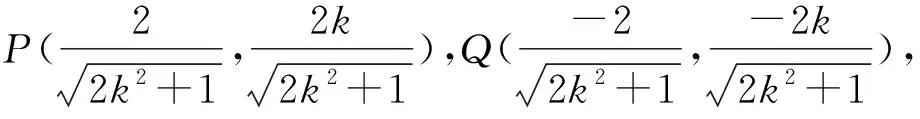
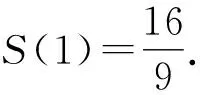
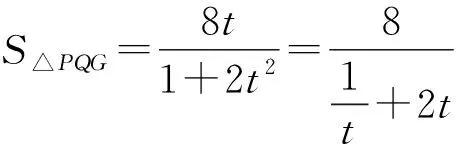
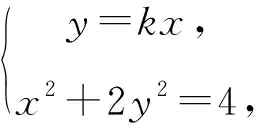
消去y,得(1+2k2)x2=4.

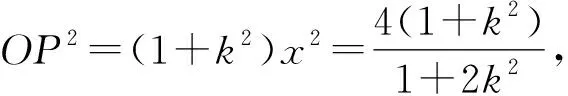
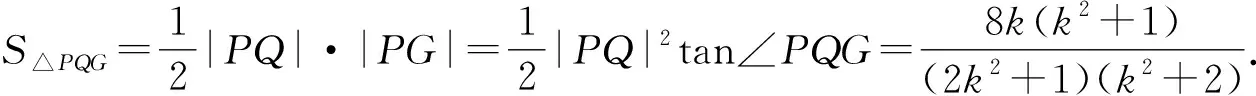
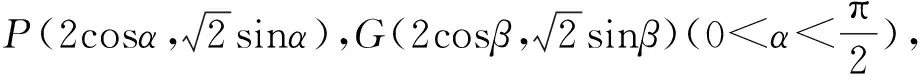
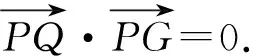
即sin2α+2cos2α=2cosαcosβ+sinαsinβ.

设θ=α-β，则sin2α+2cos2α=2cosαcos(α-θ)+sinαsin(α-θ)=2cosα(cosαcosθ+sinαsinθ)+sinα(sinαcosθ-cosαsinθ)=(sin2α+2cos2α)cosθ+sinαsinθcosα.

故(sin2α+2cos2α)(1-cosθ)=sinαsinθcosα.

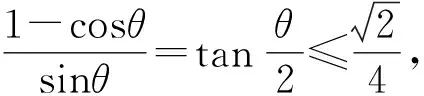
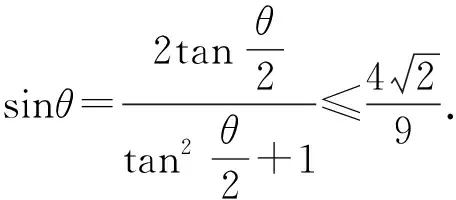
根据坐标系中三角形面积公式得

评注本题解法1比较常规，利用斜率坐标和距离求解，属于通性通法，解法2对解法1进行了优化运算，利用基本不等式求最值，换元比求导运算量小多了，解法3运用角度和距离求解，不容易想到，解法4利用椭圆参数方程进行三角换元，难度较大，但是利用三角换元求最值有时会起到事半功倍的效果，此题还可以进行仿射变换求解，在此不做赘述.作为压轴题考查了学生逻辑推理和数学运算能力.

2.2 解决定点(值)问题中的几个方法

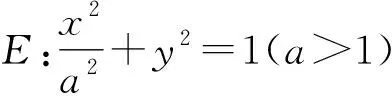
(1)求E的方程；

(2)证明：直线CD过定点.

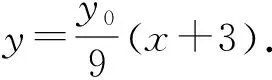
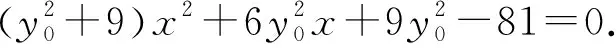
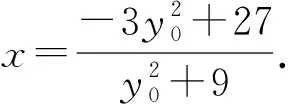
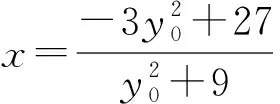
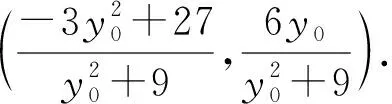
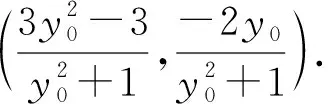
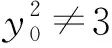
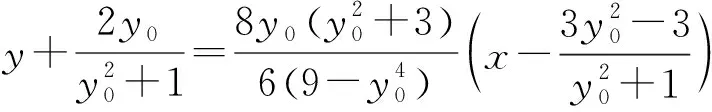
整理,得

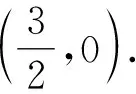
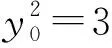
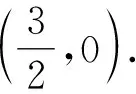
②

③

由②③,得x1y2-3y2y1=-9y1-3y2.

④

由第三定义可知：

则3x1y2-x2y1+3y1-9y2=0.

⑤

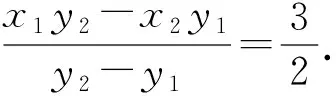
则CD的直线方程为

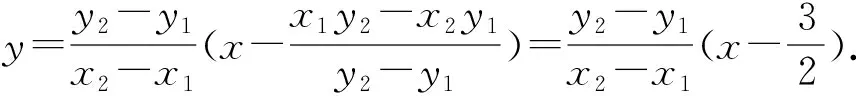
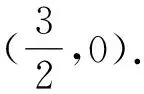
评注本题考查了椭圆的简单性质及方程思想，计算能力及转化思想、推理论证能力.也可以利用曲线系和极点极线去解决，由于通性通法比较常用，在此不再赘述.

总结提升(1)求解直线或圆锥曲线过定点问题的基本思路是：把直线或圆锥曲线方程中的变量x，y看成常数，把方程的一端化为零，将方程转化为以参数为主变量的方程，这个方程对任意参数都成立，这时参数的系数就要全部等于零，这样就得到一个关于x，y的方程组，这个方程组的解所确定的点就是直线或圆锥曲线所过的定点.(2)求定值问题常用的角度有两种：一是从特殊值入手，求出定值，再证明这个值与变量无关；二是直接计算、推理，并在计算、推理的过程中消去变量，从而得到定值.

2.3 解决弦长问题的几个视角

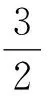
(1)若|AF|+|BF|=4，求l的方程；

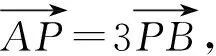
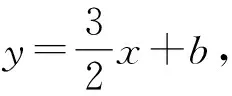
整理,得9x2+12(b-1)x+4b2=0.

故Δ=144(b-1)2-144b2>0.

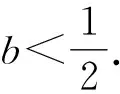
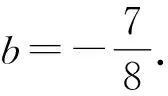
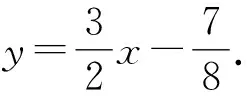
所以y1=-3y2.

整理，得y2-2y+2b=0.

所以y1+y2=2.

解得y1=3，y2=-1.

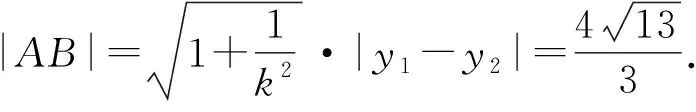
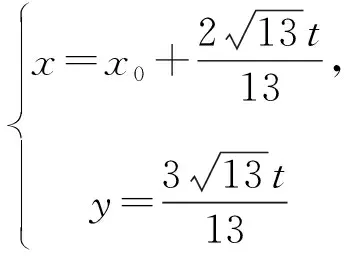
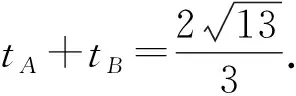
⑥

(1)因为|AF|+|BF|=4，

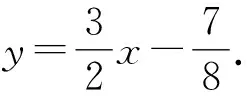
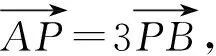
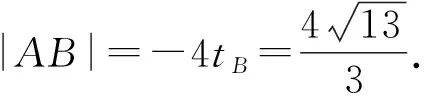
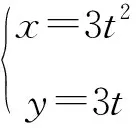
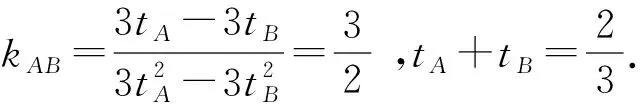
⑦

(1)因为|AF|+|BF|=4，

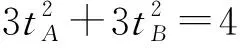
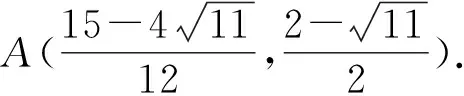
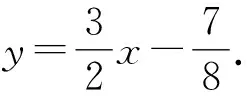
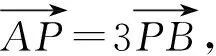
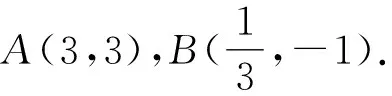
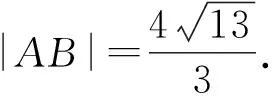
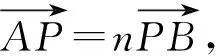
评注本题中利用直线参数方程中参数的几何意义解题尤其简单，计算量小，思维量也不大，但是对于学生来说不易想.解决此类问题常用视角有：①通性通法(利用基本概念和性质)；②设直线参数方程法；③设圆锥曲线参数方程法；④极坐标法.

在解答题中以上的总结还远远不够，比如求轨迹方程的常用方法：

(1)直接法：如果动点满足的几何条件本身就是一些几何量，如距离和角的等量关系，或几何条件简单明了易于表达，只需要把这种关系转化为x,y的等式，就能得到曲线的轨迹方程.

(2)定义法：某动点的轨迹符合某一基本轨迹如直线、圆锥曲线的定义，则可根据定义设方程，求方程系数得到动点的轨迹方程.

(3)几何法：若所求轨迹满足某些几何性质，如线段的垂直平分线，角平分线的性质，则可以用几何法，列出几何式，再代入点的坐标即可.

(4)相关点法(代入法)：若动点满足的条件不变用等式表示，但动点是随着另一动点(称之为相关点)的运动而运动，且相关点满足的条件是明显的或是可分析的，这时我们可以用动点的坐标表示相关点的坐标，根据相关点坐标所满足的方程，求得动点的轨迹方程.

(5)交轨法：在求动点轨迹时，有时会出现求两个动曲线交点的轨迹问题，这类问题常常通过解方程组得出交点(含参数)的坐标，再消去参数即可求出所求轨迹的方程.还有关于面积问题、探索性问题等，解析几何中除了通性通法还有很多视角值得研究，比如彭赛列闭合定理、阿基米德三角形和仿射变换等以高等数学为背景的初等解法值得继续探究.