例析数列问题中的“安全隐患”

⦿邢台市第十九中学 崔胜峰

数列是高中数学的重要内容，是培养学生数学素养的重要载体，同时也是高考、竞赛及其他各类考试命题的热点.学生在学习这部分知识时，经常会因忽视“安全隐患”而导致解题的失误.本文中列举这些“安全隐患”，以期起到防微杜渐的作用.

1安全隐患一：基本概念不清

例1已知数列{an}是递增数列，且对于任意的n∈N*，an=n2-λn恒成立，求实数λ的取值范围.

错解1:因为数列{an}是递增数列，所以an+1>an恒成立，即λ<2n+1恒成立.

所以，λ的范围为(-∞，2n+1).

正确1：因为数列{an}是递增数列，所以an+1>an恒成立，即λ<2n+1恒成立.

于是有<(2n+1)min.

因为n∈N*时，2n+1的最小值是3，所以λ的取值范围为(-∞，3).

点评：求参数λ的范围(或值)，应该是一个具体的范围(或数)，而不应是一个含变量的代数式.

所以，λ的取值范围为(-∞，3).

点评：用函数的观点研究数列的性质时，一定要注意其定义域是N*或其子集这一特性，因而数列的图象是一群孤立的点.

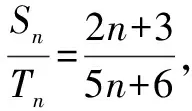
错解:设Sn=(2n+3)k，Tn=(5n+6)k,k≠0.

于是a7=S7-S6=2k，b7=T7-T6=5k.

正确1：设Sn=kn(2n+3),Tn=kn·(5n+6),k≠0.

于是a7=S7-S6=29k，b7=T7-T6=71k.

2 安全隐患二：忽视公式条件

例3已知数列{an}的前n项和Sn=3n+1，求数列{an}的通项公式.

错解:因为Sn=3n+1，所以Sn-1=3n-1+1.

故an=Sn-Sn-1=2×3n-1.

正确：当n=1时，a1=S1=4.

当n≥2时，an=Sn-Sn-1=2×3n-1.

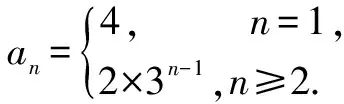
点评：由Sn求an时，一定要分n=1和n≥2进行讨论，因为a0,S0是没有意义的.解出两段后进行验证，若不能统一则要写成分段函数的形式.

例4已知等比数列{an}中，a3=2,S3=6，求通项公式an.

于是2q3-3q2+1=0，即(q-1)2(2q+1)=0.

所以an=(-1)n-124-n.

正解：当q=1时，a1=a2=a3=2,S3=6，符合题意.所以q=1时，an=2.

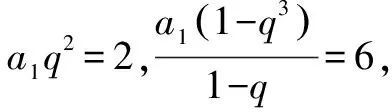
综上所述，数列{an}的通项公式为an=2或an=(-1)n-124-n.

点评：利用等比数列前n项和公式时，要特别注意对公比q=1和q≠1 进行判断[1]，以免漏掉公比q=1的情形.

3 安全隐患三：忽视隐含条件

例5首项为18的等差数列{an}，从第10项起开始为负数，求公差d的取值范围.

错解:因为a10=a1+9d=18+9d，所以18+9d<0，解得d<-2.

正解：由an=18+(n-1)d，a9≥0,a10<0，得18+8d≥0,18+9d<0.

点评：上述错解忽略了“开始”一词的含义，即第10项是等差数列的第一个负项，前9项都是非负的，所以审题务必仔细.

例6已知数列-1,a1,a2,-9成等差数列，-1,b1,b2,b3,-9成等比数列，求(a2-a1)b2的值.

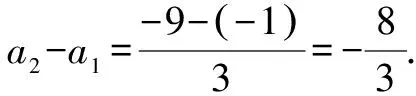
当b2=3时，(a2-a1)b2=-8；当b2=-3时，(a2-a1)b2=8.

综上所述，可得(a2-a1)b2=±8.

正解：因为-1,a1,a2,-9成等差数列，所以

故(a2-a1)b2=8.

点评：b2=(-1)q2<0是题目中隐含的条件，利用等比数列的性质解题时要特别注意这类条件.

4 安全隐患四：忽视内在规律

点评：上述错解误以为只添加一项，其内在规律是分子均为1，分母是连续的正整数，所以应增加4项.

例8求1+3+32+33+……+3n的和.

点评：数列求和时，一定要弄清楚项数，本题是n+1项而不是n项，所以要认真审题，观察出内在规律.

5 学习建议

基于以上常出现的这些失误，提出一些建议，期望在学习数列的过程中对学生有所帮助.

(1)掌握基本知识.系统掌握数列的有关概念、表示，特别是等差数列和等比数列的定义、性质和公式.

(2)掌握基本方法.数列是一类特殊的函数，因而可以用函数的思想解决求通项公式an和前n项和Sn的问题；运用方程的思想[2]，设出基本量首项、公差、公比等，列方程求解，特别注意要会用“设而不求，整体代入”来简化运算；运用分类讨论思想，如对项数n是奇数还是偶数的讨论，公比q是否等于1的讨论，等等；运用等价转化思想，如an与Sn的转化，非特殊数列通过加减项转化为特殊数列，等等；另外，如观察法，类比法，公式法，待定系数法，换元法，错位相减法，分组求和法，裂项相消法，倒序相加法的使用等.

(3)加强综合应用.把数列知识与函数、方程、不等式、平面向量、二项式定理、解析几何、概率、实际问题等相结合，提高综合运用知识解决问题的能力.