多角度计算一个三棱锥的体积
⦿甘肃省张掖市体育运动学校 张青凤
体积问题是立体几何中的一个常考问题,如何解决此类问题呢?首先,识别所要计算的立体图形;其次,分析图形的结构特征.常见的解决方法包括:公式法、割补法、向量法.对于较为复杂的图形,还可以利用等价转化法、质点几何法、祖暅原理法求解.下面通过一道立体几何模拟题来展示计算体积的各种方法.
1 题目及分析

图1
(2022届广东省12月份联考第12题改编)如图1,已知正方体ABCD-A1B1C1D1的棱长为2,M,N分别是AD,CC1的中点,P,Q分别是线段AB,C1D1上的点,且AP=2PB,C1Q=2QD1,求三棱锥Q-PMN的体积.
分析:本题所需求体积的几何体为一个三棱锥,如果直接选择公式求解,其难度主要集中在“高”的运算上.对于高的运算,可利用几何法即通过空间中线面间的位置关系构造出“高”再进行计算;或利用向量进行计算.
2 解题探析
方法1:通过计算三棱锥的高来计算体积.
因为在本题中利用几何法计算三棱锥的高需要构造较多的辅助线,且证明过程较为冗长.本文中不运用该方法求解.仅介绍如何利用向量法求解.

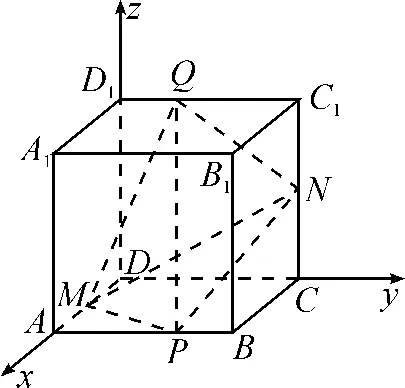
图2
如图2,以D为原点,以直线DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系.



图3


方法2:割补法求解.
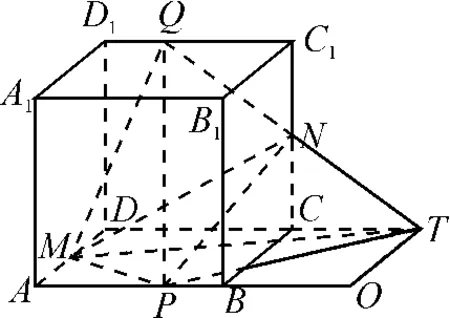
图4
如图4,延长QN,DC相交于点T,连接MT,PT.考虑三个三棱锥Q-MPT,Q-MPN,N-MPT.根据体积的可加性知VQ-MPN=VQ-MPT-VN-MPT.
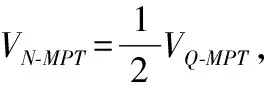
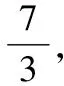
方法2中除了运用割补法外,还体现了等价转化的思想.接下来将介绍等价转化法的一般策略.
方法3:等价转化法.
根据三棱锥的体积公式,可知等底等高的三棱锥体积均相同.为此,可以从构造高的视角进行转化.
如图5-1,设点E为B1C1的中点,易得QE∥MP,从而QE∥平面PMN,因此VQ-MPN=VE-MPN.

图5-1

图5-2

通过上述解析可知,割补法与等价转化法常常混合使用.
方法4:质点几何法[1-2].
质点几何法的本质是给立体图形中的各点按线段间的比例赋予一定的质量,再利用质点间的运算法则计算所形成图形的面积或体积.
因为M,N分别是AD,CC1的中点,所以可设
2M=A+D,2N=C+C1.
①
又因为AP=2PB,C1Q=2QD1,所以可设
3P=A+2B,3Q=C1+2D1.
②
由上述①②中四个方程质点间的运算,可得
36QMPN=(A+D)(C+C1)(A+2B)(C1+2D1),
③
其中QMPN表示三棱锥Q-MPN的体积,对于③式右侧展开式中出现相同点或四点共面的情形时,其对应的体积即为0.据此可知,上式右侧展开后剩余的项为
2ABCC1+4ABCD1+ADCC1+2ADCD1+2BDCC1+4BDCD1+2ADC1D1+4BDC1D1.
④
3 解后反思与教学建议
上述的解答过程体现了研究立体几何中体积问题的各种视角.除了上述方法外,还可利用向量的混合积以及祖暅原理进行求解.
为了突破这一难点,笔者认为可以从以下几个方面入手.教师要带领学生识图,分析图形的结构特征,根据图形的特点选择恰当的公式进行运算.现阶段因为信息技术在教学中的应用,所有的立体图形都可用GeoGebra等数学软件进行绘制.学生可从视觉上直观感受图形的变化以及形成过程.一方面要在教学中灵活地运用相关软件,提升教学效率;另一方面,也要培养学生基本的绘图原理,在绘制的过程中感受各种几何量的形成过程以及依存关系.
在体积的运算过程中,还常常涉及面积等平面几何的知识.在该板块的教学中,要带领学生复习解三角形及平面几何中的有关知识以及运算技巧.例如,在上文中利用割补法计算△MPT的面积时,可将其理解为四边形AOTD中的图形,结合平面图形的性质即可快速求解.
最后,在教学中要带领学生开拓视野.如上文中的质点几何求解法,其本质是构建了一套新的运算法则与规律.在教学中,可通过平面图形中的面积运算类比至立体几何中的体积运算.

