风电输出功率预测技术研究综述
武煜昊,王永生+,徐 昊,陈 振,张 哲,关世杰
1.内蒙古工业大学 数据科学与应用学院,呼和浩特 010080
2.内蒙古自治区基于大数据的软件服务工程技术研究中心,呼和浩特 010080
随着化石能源的日益消耗殆尽,清洁可再生能源成为各国发展的重点。风能以其存储量大、可再生的特点得以快速发展,仅2021 年全球新增装机容量高达97 272 MW,相较于2020年增加约13%[1]。
风能具有间歇性、高可变性及强随机性等特点,对电网并网造成负面影响。提前进行风电功率预测是降低风电并网影响的方式之一,因此对于高精准度、低时延性风电功率预测技术成为目前研究中的一大重点[2]。采集过程中不可控因素的存在,使得采集到的原始风电数据中存在异常数据及缺失数据。这些异常数据对参数估计及未来预测造成不可或缺的影响。在风电技术研究中,对采集到的数据进行相应的数据预处理操作后再进行相应的预测(如图1所示)。其中数据的质量对预测结果效果产生极大影响,因此在进行风电功率预测前通常进行相应的异常值检测和缺失值插补操作。
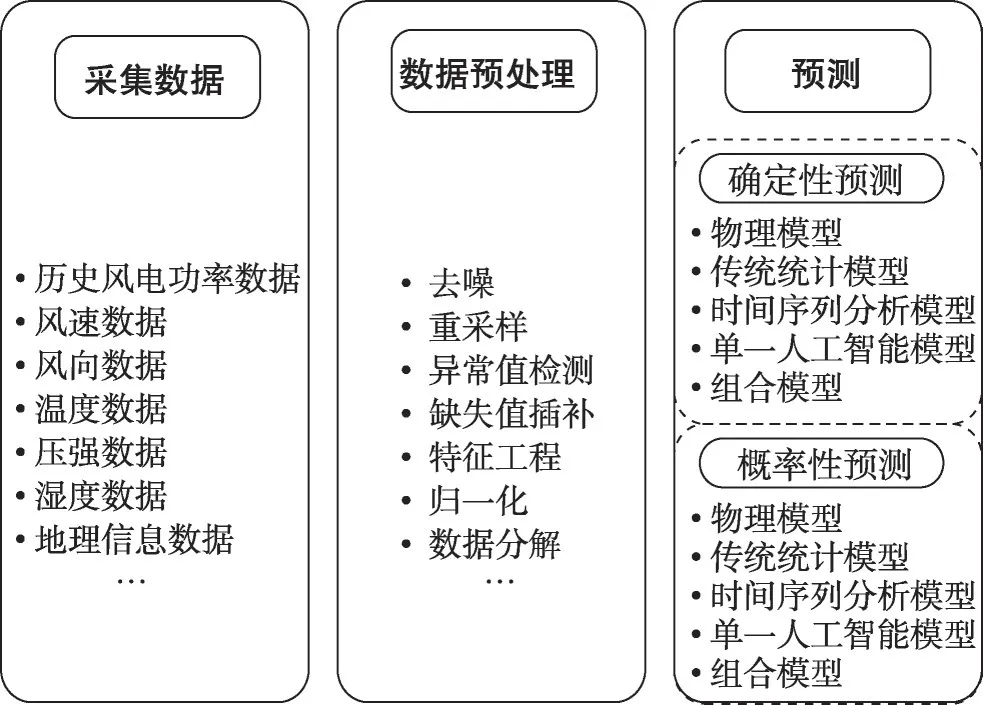
图1 风电输出功率预测流程Fig.1 Flow chart of wind power output forecasting
本文对风电输出功率预测中异常值检测、缺失值插补和风电功率预测模型的理论方法进行梳理,并对其中重要的研究方向进行介绍。
1 异常值检测技术
异常值指处在特定范围外明显偏离该样本数据集其余观测数据偏离的个别数据[3]。异常数据有点异常、子序列异常和序列异常三种,这些异常值的存在会显著影响预测模型的性能,降低预测值的可信度[4]。异常检测则是在数据中寻找不符合预期行为的数据的过程[5],采用相关的异常检测算法对原始风电数据中的异常数据进行准确识别[6],为预测提供更精准的数据。
本章主要从异常检测方法和异常数据解释技术两个方面进行介绍,并对相应的方法发展进行总结与展望。
1.1 异常检测方法
目前,异常值检测方法可分为全监督[7]、半监督[8]和无监督[9]三种学习方式。在工业数据检测领域数据集中,特别是在风电领域中,采集数据种类多,时序长,依靠人工标注数据集的监督学习和半监督学习可行性及适应性较低,因此在现有时序数据异常值检测领域(特别涉及风电原始数据异常检测领域)中,大多数检测算法采用无监督方式的检测技术。
根据处理技术的不同,异常检测方法大致可分为基于概率统计的异常检测方法、基于聚类的异常检测方法、基于距离的异常检测方法、基于密度的异常检测方法、基于偏差的异常检测方法和基于集成的异常检测方法。本节主要对不同检测方法进行分析介绍,并对该领域异常检测方法未来挑战进行分析。目前现有研究中,通常采用精准率[10]、召回率[11]及F1-score[11]等评价算法效果[12],相应文献中均有介绍,本文不再详细阐述。
1.1.1 基于统计的异常检测方法
基于统计的异常检测方法通过对数据中变量进行描述性的统计,以此判断数据是否异常。基于统计的异常检测方法有两种:使用参数的异常检测方法和非参数的异常检测算法[13]。
(1)简单统计量分析法通过统计数据集中各变量(特征)特点(如最大值、最小值等)判断该数据是否为异常。文献[14]使用简单统计量分析法将数据按照不同风向等分别进行统计,并根据所设置的阈值进行异常判别。该方法直观上简便易懂,但仅适用于数据量小且集中型的数据,检测方式粗糙难以满足实际需求。文献[13]中的HBOS(histogrambased outlier score)算法将数据样本根据特征分成多个区间,计算每个数据的异常得分,样本少的区间异常的可能性较大。与其他异常检测算法相比,该算法运行时长较短,特别在大量数据检测中具有明显优势。整体来看,基于简单统计量分析的检测方法适用于不在有效范围内大量堆积的风电原始数据,数据量过大或数据分散时并不适用[15]。
(2)3σ准则又称拉依达准则。当数据为正态分布时,分布在(-∞,μ-3σ)和(μ+3σ,+∞)中的概率仅占不到0.3%,因此可以认为分布在该区间内的数据为异常数据[16]。前期风电研究中常采用3σ进行异常值检测[17]。3σ算法简便、计算速度快且可以较好地识别极端数据,但在一些实验结果中显示该算法整体检测准确率一般,通常为30%左右。实际中风电数据原始分布并不完全服从正态分布,因此3σ准则在风电数据异常检测中识别出的异常数据值远小于实际存在的异常数据。
基于统计的异常检测方法所存缺陷:(1)需提前确定数据分布,如正态分布等。风电数据并不完全服从正态分布,此类异常检测方法在风电数据异常检测领域适用性较差。(2)对于模型的选择要求十分严格,模型选择对最终检测结果影响很大。这使得基于统计的异常检测方法在实际应用中存在许多困难。
1.1.2 基于聚类的异常检测方法
基于聚类的异常检测方法通过聚类算法对数据进行聚类,将未归类的数据及数据少的类判定为异常[18]。目前常用的聚类方法有K-means、高斯混合模型(Gaussian mixed model,GMM)及DBSCAN(densitybased spatial clustering of applications with noise)[19]等。
K-means 算法与马氏距离结合的方式用于检测风机中的多元异常值[20],但K-means算法聚类类别及聚类中心值选取的不同对最终结果产生较大影响。针对上述问题,文献[21]提出DPC(clustering by fast search and find of density peaks)算法,以解决传统Kmeans 中需提前进行初始化聚类类别个数对结果造成影响的问题。该算法能够快速发现密度峰值点,适用于大量数据的聚类分析。为解决DBSCAN中需设置关键参数半径和邻域密度阈值的问题,文献[22]提出基于自适应密度聚类的异常检测算法。该算法避免了人为原因造成的误差现象,更高精度地识别出风电机组数据中存留的异常数据。
整体来看,基于聚类的异常检测方法模型虽具有较强的迁移能力,但检测所需时耗较长。同时,此类算法大多以单点形式进行检测,并未挖掘时间序列间的时序性信息。
1.1.3 基于距离的异常检测方法
基于距离的异常检测方法通过计算每个数据间的距离,当检测数据与其他数据之间距离较大时将该数据认定为异常[23]。此类算法是目前机器学习方法中应用最为广泛的算法之一,其中K近邻(K-nearestneighbors,KNN)算法最为常用。
KNN算法广泛应用于风电数据异常检测中。针对KNN算法计算量大、异常值检测时间长的问题,文献[24]提出一种基于反向最近邻的数据流异常检测算法。该算法结合时序窗口,进一步提高了KNN 检测的速度。针对流式数据,文献[12]提出一种通过时间滑动窗口构建非欧几里德对,以此判断当前时刻点数据是否异常的AnomalyDetect 算法。该算法虽具有不错的效果,但仅适用于互联网运维、病人心电图等依据历史数据对比的异常检测中,整体应用受限。文献[25]将KNN 异常检测算法与四分位距方法、3σ方法进行对比分析,证明普通机器学习模型中,KNN 用于异常检测的效果最优。此外,基于KNN 的异常值检测算法应用于网络异常检测[26]、区块链异常交易[27]等领域。
通过分析发现,基于距离的异常检测方法早期研究中占有重要位置,但该方法对参数敏感程度高,若没有数据的先验知识,难以获得理想的检测结果且该类方法无法区分数据异常的程度。
1.1.4 基于密度的异常检测方法
基于密度的异常检测方法作为基于距离的异常检测方法的改进,通过数据局部的密度信息判断数据是否异常。目前常见的方法有:LOF(local outlier factor)[28]、INFLO(influenced outlierness)[29]、LoOP(local outlier probability)[30]等。
文献[31]采用LOF 算法实现原始风电数据的异常检测任务,该算法作为经典的异常检测方法之一,算法简单、直观且要求条件少,可以很好地量化各个数据点的异常程度;但数据庞大时计算时间复杂度过高,同时针对时间序列的时序性信息挖掘较差。为进一步提高LOF算法的检测效果,文献[32]采用基于主成分的LOF 计算风机每个区段的异常程度,但该算法中k值选取对检测效果存在极大的影响。Zhang 等[33]也在LOF 的基础上提出一种基于相关子空间的上下文异常检测算法,通过利用局部数据属性维度的局部稀疏度重新定义相关子空间,并根据这些子空间的属性维度视作数据对象的上下文信息,以此检测隐藏在子空间中的上下文敏感异常值。这些算法进一步提升了模型的检测效果。为提高算法运算效率,Bai 等人[34]采用网格划分(girdbased partition,GBP)算法将原始数据分为多个网格,再采用DLC(distributed LOF computing)方法进行异常值检测。
整体来看,相较于上述其他检查方法,基于密度的异常检测方法在检测效果上有进一步提升,但整体计算时长较高,同时仍保留基于距离的异常检测算法所具有的参数选取敏感的缺陷。
1.1.5 基于偏差的异常检测方法
基于偏差的异常检测方法包含基于序列的异常检测和基于预测的异常检测两种[18]。
(1)基于序列的异常检测方法原理是当相邻序列中存在明显的偏差时,将该数据标记为异常。SCREEN(speed constraint-based stream data cleaning)模型[35]通过在两个连续值之间建立最大和最小可能斜率判断股票价格数据中是否存在异常。但风电原始数据中风速、风电输出功率等具有高随机性和波动性,在部分区间内相邻数据存在大幅度偏差,因此该类型的异常值检测方法并不适用于风电数据。
(2)基于预测的异常检测方法[19]根据预测值与实际值间误差值来判断数据是否异常,改善传统基于距离和密度的异常检测技术无法检测流数据中常见周期性和季节性相关的点异常。该类型的检测方法原理是通过预测模型对风电输出功率数据进行拟合,并根据拟合后的曲线对异常值进行判别。但此类方法对于模型的预测效果要求极高,同时异常检测效果与其他方法相比较低。
文献[10]提出LSTM-AE 异常检测模型,长短期记忆单元(long short-term memory,LSTM)作为AE的隐藏神经元,并结合支持向量回归(support vector regression,SVR)进行阈值的自适应。该模型改善了单一预测异常检测方法中拟合差、阈值设置选取不当的问题,进一步提高自编码器(auto-encoder,AE)模型的异常检测效果,但是其未考虑随机变量间的时间依赖性,且原始AE模型生成样本具有较强的不确定性,使得模型仍有进一步优化的空间。Munir等人[36]提出的DeepAnT 异常值检测方法,通过卷积神经网络(convolutional neural networks,CNN)预测后计算与实际值间的欧氏距离,以判断此时间戳是否异常。该模型可以在相对较小的数据集上进行训练,具有良好的泛化能力,但当原始数据中异常值过多时,CNN会对异常数据进行建模,出现些许异常数据无法准确识别的现象。模型参数更新是提升预测效果的关键之一,但定期或每次到达新点时,重新训练以适应数据变化的方式增大模型的计算开销和存储成本,同时容易造成模型过时。针对这一问题,在现有研究中常采用在线增量学习方式,保持模型参数最新的同时降低数据存储和维护的成本[37]。
整体来看,基于偏差的检测方法与模型拟合效果成正相关,整体效果与其他类型的检测方法相比仍存在一定差距。
1.1.6 基于集成的异常检测方法
随着数据涉及领域的增加,整体数据维度不断扩大。现有文献中针对多变量时序数据检测常采用单变量检测技术进行识别,这一方式导致变量间相互依赖关系丢失。基于集成的异常检测方法[38]可以较好地改善上述问题。该算法是通过结合不同异常检测算法的优点,提高模型的鲁棒性和异常检测的效果。降维(将原始高维数据集转换为一维互相关函数后判断数据是否异常[39])、AE等应用于多元数据异常检测中。
Sakurada 等[40]构建了一种具有非线性降维的自编码器,用于航天器数据的异常检测,并与其他降维异常检测模型进行对比。针对该模型并未考虑多变量内部的时序性的问题,Kieu 等人[41]提出一种基于CNN 和LSTM 的AE 框架用于检测驾驶员行为数据中的异常值,结合滑动窗口和自编码器以实现更高准确度的检测。CNN-AE 充分地对每一矩阵进行信息提取,但无法捕获矩阵间的时序信息,而LSTM-AE克服了这一限制,进一步提高了模型的检测效果。针对多元时序数据异常检测效果差的问题,Su 等[42]提出基于门控循环单元(gated recurrent unit,GRU)和变分自编码器(variational auto-encoder,VAE)的检测方法,并采用Planar NF(planar normalizing flows)改善VAE 只能生成高斯分布数据的不足,同时结合随机变量连接进一步挖掘隐变量间的时序性。相较于上述LSTM-AE 等简单结合的AE 模型,该模型结合的随机变量连接使得映射后的随机变量保留原始数据的时序性信息,进一步提高了VAE 模型的检测效果,但该模型并未考虑数据特征间的相关性影响。文献[43]提出一种模糊聚类算法与概率方法相结合的风电数据过滤技术,用于在线检测有效数据。相对于传统单一异常检测方法在生成建模精度方面有效性有所提高,但参数选取对最终结果产生决定性影响,因此如何精准地进行参数选取显得格外重要。针对现有检测算法中子序列固定不变的问题,SLADETS和SLADE-MTS可以自动识别异常事件序列及其确切的可变长度异常子序列,防止传统算法中固定子序列问题及可变子序列中异常子序列在其他维度序列下误判为正常情况的发生[44]。
基于集成的异常检测方法博众家所长,相较于其他单一检测方法具有较高的精准度和较好的鲁棒性。此类方法也是目前时序数据研究中的重要方式之一。
1.2 异常数据解释技术
随着异常值检测技术的日益复杂,异常值检测模型和结果的解释开始受到研究人员的关注。异常解释有助于运维人员及时发展故障所在,及时进行修复工作。
根据风速-风电功率数据的分布特征,正常数据分布在风速-风电功率曲线附近,而异常数据常显示为横向数据带的聚集分布且明显偏离风速-风电功率曲线。异常类型主要有四类(如图2所示),第一类至第四类异常存在的原因分别是计划外的停机检修和风机零件故障[22]、弃风限电[45]、传感器故障[15]、气象波动等[46]。

图2 风速-风电功率分布曲线Fig.2 Wind speed-wind power distribution curve
近年来,机器学习等技术成为实际应用中的重要工具,研究人员越来越重视机器学习模型工作机制的研究,对于异常数据的解释性研究日益增多。时序数据中异常值的存在显著影响后期预测效果,尽管现在用于时序数据异常值检测技术众多,但对于检测到的异常值进行解释及其潜在的生成机制远未解决。文献[47]尝试采用聚类算法对异常数据进行分析解释,但这一方式无法量化每一特征对异常的影响程度。基于此,文献[10]通过计算原始数据单个变量与性能指数间的关联性,根据排序结果确定影响异常的特征参数。文献[42]通过对每一时刻单变量重构概率值求和计算当前时刻数据的异常性,并根据单变量重构概率判断该变量对整体的影响程度,以此给出对当前异常产生影响的变量排序。该方法通过神经网络重构来解释数据异常的可能性,可以迁移至其他多变量时序数据的异常检测算法中。与之相似的是,文献[48]同样采用每个维度的重建误差来分析和解释异常。由于原始数据中异常数据的存在,导致这类依靠原始重建概率方式判断异常方法中的一些正常数据得到较差的重建,以此用于解释异常的方式存在偶然性。针对这一问题,文献[49]通过计算窗口内数据多次重建概率均值,并在整个窗口的数据中寻找重建误差较大的时刻点作为异常来源。这一方式通过多次基于马尔可夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)的解释过程可以减轻严重异常的影响,提高了整体异常检测的效果。此外,文献[50]认为数据来源于正常和受污染两种方式,采用改进的SIF(single-valued metric based on the influence functional)方法计算当前数据异常的可能性。这些方法或通过寻找多变量中每一特征的影响大小来解释异常的原因,或计算单值指标来衡量异常值对未来预测的影响大小。
1.3 异常值检测方法问题与展望
现有异常值检测方法对比效果如表1 所示。针对现有方法中存在的一些问题与不足,认为以下几点或将成为未来研究中的重点。

表1 风电机组异常检测方法对比Table 1 Comparison of wind turbine anomaly detection methods
(1)阈值自适应:部分模型检测方法(如基于统计、聚类的异常检测方法等)需提前对异常阈值进行设置,参数选取得过高或过低均将会降低模型的准确率,因此如何准确进行阈值的自适应选择尤为重要。
(2)时间响应:尽管许多基于集成的异常检测方法在效果等方面取得较为不错的成绩,但针对实际需要,其整体响应时长仍存在降低空间。较短的时间响应意味着及时提醒,便于运维人员进行查验、维修。因此,短时间的异常检测响应是必要的。
(3)单变量检测技术迁移问题:多变量时序数据异常检测方法研究中多数采用单变量检测技术对不同变量分别进行检测,如基于统计、聚类、距离等检测方法,这些方法造成特征间相互性信息丢失,可能出现单变量检测正常而实际异常情况的发生。如何将单变量检测技术迁移至多变量数据中,充分挖掘变量间相互性关系将是关注的重点之一。
(4)时序数据不规则采样的异常检测问题:由于不同特征数据采集时采样频率的不同,需要对不同特征数据进行重采样。重采样过程中通常会造成数据信息的缺失,这对后期数据挖掘的效果产生一定影响。因此,如何针对不同采样频率的数据进行异常检测将是一个可观的研究思路。
(5)异常解释机制问题:近些年来,随着深度学习技术的快速发展,异常检测模型逐渐复杂化,而对于检测结果的异常解释机制仍未解决。异常解释可以为运维人员提供相应的提示,以便于更短时间内筛选出数据异常原因。因此认为,针对检测结果的异常性,其解释的研究或将成为未来研究中的一个重要方向。
2 缺失值处理方法
数据采集过程中常伴随数据缺失现象,小规模的数据缺失虽对后期分析挖掘影响不大,但大量数据的缺失使得数据分析挖掘变得困难,因此对缺失数据的插补及插补质量格外重要。针对不同情况的缺失,处理方法也有所不同[51]。为有效地评估插补后数据效果,现有研究中通常采用平均绝对误差(mean absolute error,MAE)、平均绝对偏差(mean absolute differences,MAD)[52]、准确率r等进行评价。
本章主要对不同处理技术的异同及适用情况进行讨论,并在最后对未来研究中可能存在的挑战进行分析。
2.1 常规处理方法
常规处理方法包含直接删除法、均值插补法、零值插补法、上一次观测值插补法等。这一类处理方法通常操作简单且计算复杂度低,但存在一定局限与不足。如直接删除法将原始数据中的缺失样本进行删除,使得整体数据规模减小,缺失率提高,造成数据信息丢失,进而影响数据挖掘效果。这一方法适用于缺少样本数量较小的情况,但为更好地挖掘数据中的信息,并不建议采用该方法;而均值插补法、零值插补法、上一次观测值插补法等忽略了不同特征间的相互关联程度,改变原始数据分布,缺乏对时间信息的利用,使得这类插补方法适用面较小。
2.2 基于辨别式的插补方法
辨别式的插值方法是将模型估计的缺失值填充至缺失位置的方式。这类方法包含回归插补法(线性回归、非线性回归等)、递推式非邻均值补全法[53-54]、三次样条插值法、链式方程多元插值(multiple imputation by chained equations,MICE)、矩阵分解(matrix factorization,MF)、多层感知机(multilayer perceptron,MLP)[55]、KNN、循环神经网络(recurrent neural networks,RNN)及其改进等。
基于线性回归的插补方法容易构造且计算量小,但实际数据中大多数并不满足线性条件,使得基于线性回归的插补方法并不符合实际应用。非线性回归插补方法相较于常规处理方法来说精度进一步提升,同时适应性更广,但并未考虑特征间相互性,且数据间信息挖掘并不充分,主要作为粗糙插补使用。
三次样条插值法原理是将原始区间分为多个连续的子区间,每个子区间由一个三次多项式函数进行拟合。同时需要满足在区间边界节点的两边具有相等的一阶和二阶导数,以便插值是两次全局连续且可微的[56]。文献[57]采用三次样条插值法对风机功率曲线进行拟合,并与制造商功率曲线进行对比。这种插值方法插值节点处函数值的波动仅对该点两边的分段存在影响,对于其他较远分段影响会逐渐减小,因此该方法具有较好的稳定性。同时相比深度学习方法,三次样条插值法等数学方法训练量更小,建模更为简单。相对其他数学方法而言,三次样条插值根据空缺值附近的观测数据,使用具有良好平滑性的插值函数进行缺失值插补,使得插补后的数据具有良好的平滑性。当缺失值所处区间平滑性较差时,该方法不能准确反映真实数据[58],同时随着区间大小的增加,模型的性能会有所下降。
MICE 方法通过多次插补降低单次插补造成的标准误差,但仅适用于随机缺失(missing at random,MAR),完全随机缺失(missing completely at random,MCAR)等缺失并不适用[59]。Yu 等人[60]在MF 的基础上结合时间正则化提出TRMF(temporal regularized matrix factorization)插补框架,并在电力及交通数据集上验证了该框架的有效性。此外,基于MF的插补模型被应用于降水数据[61]等。但整体来看,MF 方法需保证原始的共现矩阵是稠密的,无法使用于大量缺失情况下。同时该技术未挖掘上下文特征间的相互性,丧失部分的有效信息。
基于均值插补、回归插补、样条插补等传统插补方法往往存在较大的偏差和误差率,特别是当数据长时间连续缺失情况下,插补效果极差。随着机器学习技术的快速发展,基于机器学习技术的支持向量机(support vector machines,SVM)、MLP、KNN、RNN及其改进的模型等应用于时序数据缺失值插补中。如文献[62]提出相关向量机插补模型,相对于常规插补方法,进一步挖掘数据特征与功率值间的关系。文献[63]将模糊推理与神经网络进行结合,提出的ANFIS(adaptive neuro-fuzzy inference system)模型进一步提高了插补的准确率。
MLP 由多个神经元构成,前一层的输出结果作为后一层神经单元的输入,MLP 在数据处理中具有良好的适用性,无需进行模型假设,同时在估计噪声模型时具有很大的灵活性[64]。文献[65]对统计线性插值、样条插值、线性模型和MLP插值进行对比。结果发现,线性插值法在短期数据缺失插补中效果最优,MLP次之;在长期数据丢失情况下,线性插值、样条插值和回归插值效果有所下降,但MLP 的精度保持稳定。文献[66]采用MLP 对长时间连续缺失的空气质量数据进行回归建模,实验发现连续缺失时间越长,MLP 相较于回归插补等传统插补方法的插补效果越好。但MLP的隐藏节点个数选取仍是目前研究中的一大难题,同时其伴随着学习速度慢、易陷入局部极值的缺陷。
KNN 作为机器学习中最为常见的插补算法之一,整体计算成本高,同时很少考虑两个变量间的相互关系。针对这一问题,SPCA+GKNN[52]方法在KNN 基础上考虑到多变量间的相互关系,同时自适应K值选择,以此提高KNN插值效果。Che等[67]中的GRU-D 模型在GRU 的基础上结合mask 和time interval(时间间隔)来捕获缺失信息,同时计算时间和空间复杂度相似于RNN,但该模型对一般数据集有诸多限制。此外,M-RNN[68]利用双向RNN 对缺失数据进行估计。该模型将估计值当作常数进行固定,无法进行更新,同时该模型丢弃了缺失变量之间的关系。与M-RNN 相似的是,BRITS(bidirectional recurrent imputation for time series)[69]根据其历史数据及邻居数据的测量值估计缺失值的测量值。BRITS虽考虑时间及多特征因素,但并不能很好地应对高缺失率的情况,无法保证准确的预测[70-71]。
2.3 基于生成式的插补方法
基于生成式的插补算法是通过学习数据的联合概率分布密度,再求解条件概率分布的方法。目前基于生成式的插补方法主要包含基于EM(expectation maximization)的插补算法、基于AE 的插补算法和基于生成对抗网络(generative adversarial networks,GAN)的插补算法等。
EM 插补算法迭代计算期望E 和最大化M 以获得插补数据。该类算法整体计算简单、填补精度较高,但对整体数据集依赖性较强,很少考虑两个观测值之间的时序关系。如文献[72]中要求原始数据为离散数据,当数据为连续数据时无法很好地适用;文献[73]结合EM 算法和遗传算法,在输入变量间几乎没有或没有相互依赖的情况下具有较好的表现效果。
近年来,深度学习已被证明能够捕捉复杂高维数据的潜在表示,使用神经网络生成模型插补缺失数据逐渐成为主流。AE(自编码器)等作为较为常用的生成模型,将原始数据通过Encoder 和Decoder 后重建原始数据,以完成缺失值插补操作。基于AE的插补模型种类较多,且风格各异。如ELM-AE[74]在AE 的基础上结合ELM(extreme learning machine)网络进行插补实验。该方法结合了ELM训练速度快和AE重构的特点,相较于辨别式的插补方法性能更好,但该方法需足够的完整数据集来保证模型的训练效果,整体应用受限。Lai等[75]基于AE提出TFAE(trackingremoved autoencoder)框架,重新设计隐藏单元用于不完整数据插值训练。该方法消除了网络的自追踪性,但并未考虑数据间的时序性影响,同时该算法在缺失率较大的数据集中的应用效果更好。传统AE模型通过潜在空间重构原始数据分布,将生成的伪时间序列值填充至缺失部位。
VAE 在AE 的基础上进行优化,对AE 重构损失中的潜在表示添加约束,增加了生成样本的不确定性。针对现有数据种类繁多、类型复杂问题,Gondara等[76]提出一种基于深度去噪自编码器的多重插补模型,可适用于不同数据下的不同缺失条件/机制中。该方法改善AE 模型需大量完整原始数据训练的缺陷,但重构后的数据无法确定是否保留原始数据特点间的相互性。对于家庭用电负载数据不规则问题,文献[77]提出一种基于DLP(daily load profile)的缺失值插补框架。该框架不需要迭代地对多个缺失值进行插补或确定适当的聚类和K值。文献[78]假定原始数据可以从潜在空间中生成,采用VAE 学习生成数据分布的缺失数据,以此作为预测前的预处理步骤,证明VAE 的插补提高了后期的预测性能。该方法解决了自编码器中非正则化潜在空间的问题,但同时使得潜在分布为正态分布,难以满足风电数据等不完全满足正态分布的数据特点。针对现有文献中没有关于如何在深度生成模型的训练过程中合并缺失数据的明确讨论,Nazabal 等[79]提出的HIVAE(heterogeneous-incomplete VAE)框架可以有效结合不完整数据和异质的观察结果。
此外,GAN 网络作为生成模型中的一大重点模型,可以学习数据的潜在分布,并能够从随机的“噪声”中生成“真实”的样本数据。与传统网络插值算法训练需要完整数据不同的是,GAN 能够在原始数据不完整的情况下仍很好地运行,但其生成器易生成多种分布数据。为更好地训练模型,GAIN(generative adversarial imputation nets)[80]在GAN 网络的基础上添加“hints”为鉴别器提供额外的信息,以确保生成器生成最接近原始数据分布的数据。该方法充分挖掘原始数据分布特点,但并未考虑数据间时序性特点,适用于非时序数据缺失插补中。
VIGAN(view imputation via generative adversarial networks)[81]结合CycleGAN 和DAE(denoising autoencoder)用于多模态数据插补,但风电等相关时序数据通常为单模态数据,直接迁移的效果并不理想。而GAN网络训练不稳定的缺陷也是目前研究中的重点之一,Che等[82]提出MaliGAN模型,用于解决GAN网络训练不稳定、离散数据变量反向传输困难的问题。这几种模型虽在一定程度上解决GAN网络在时序数据插补中存在的一些问题,但仍未考虑数据间的时序性影响。针对这一问题,Luo等[83]提出一种基于GRUI(gated recurrent unit for data imputation)神经单元的GAN网络用于多元时序数据插值。同时采用Wasserstein 距离的WGAN 提高学习阶段的稳定性,摆脱模式崩溃的问题,以便于GAN 模型的优化。文献[84]提出基于WGAN 的插补模型,该模型生成器部分使用多头自注意力机制(multi-head self-attention,MSA)进行AE 搭建,以学习数据的时序信息,解决RNN中无法并行运算且长时间出现遗忘问题。但此模型整体计算复杂度高,针对这一问题,文献[84]结合ProbSparse自注意力机制和VAE进行插补实验,实验结果得知两组模型效果相近,但VAE-PSA(VAEprobsparse)模型时间效率更优。此外,MaskGAN[85]、SeqGAN[86]等基于GAN 改进的模型用于文本填补等领域。
从上述文献中可以看出,相较于传统AE 模型,GAN网络插补效果更优,但其存在训练不稳定、不可逆且不提供密度估计的缺陷。但并不说明AE 模型效果完全差于GAN 模型,如VAE 作为AE 模型的一种改进,以概率的形式描述潜在空间观察,取得与GAN类似的效果,同时避免了GAN网络训练不稳定的缺陷。
2.4 基于物理特性的插补方法
基于物理特性的插补方法通过采用临近风场/风机数据进行插补。如文献[87]采用临近风电场的数据进行填补,并与多点三次样条插值方法进行对比,结果表明当临近风电场距离较近时插补效果优于基于统计学的插补方法。文献[88]采用相邻风电场的功率值对本风电场缺失数据进行插补。这类方法虽然简便,但对风机、地形等信息要求严苛,因此在整体研究中应用较少。
2.5 缺失值处理方法的问题与展望
现有缺失值插补方法对比效果如表2 所示。针对现有方法中存在的一些问题与不足,以下两点或将成为未来研究中的重点方向。
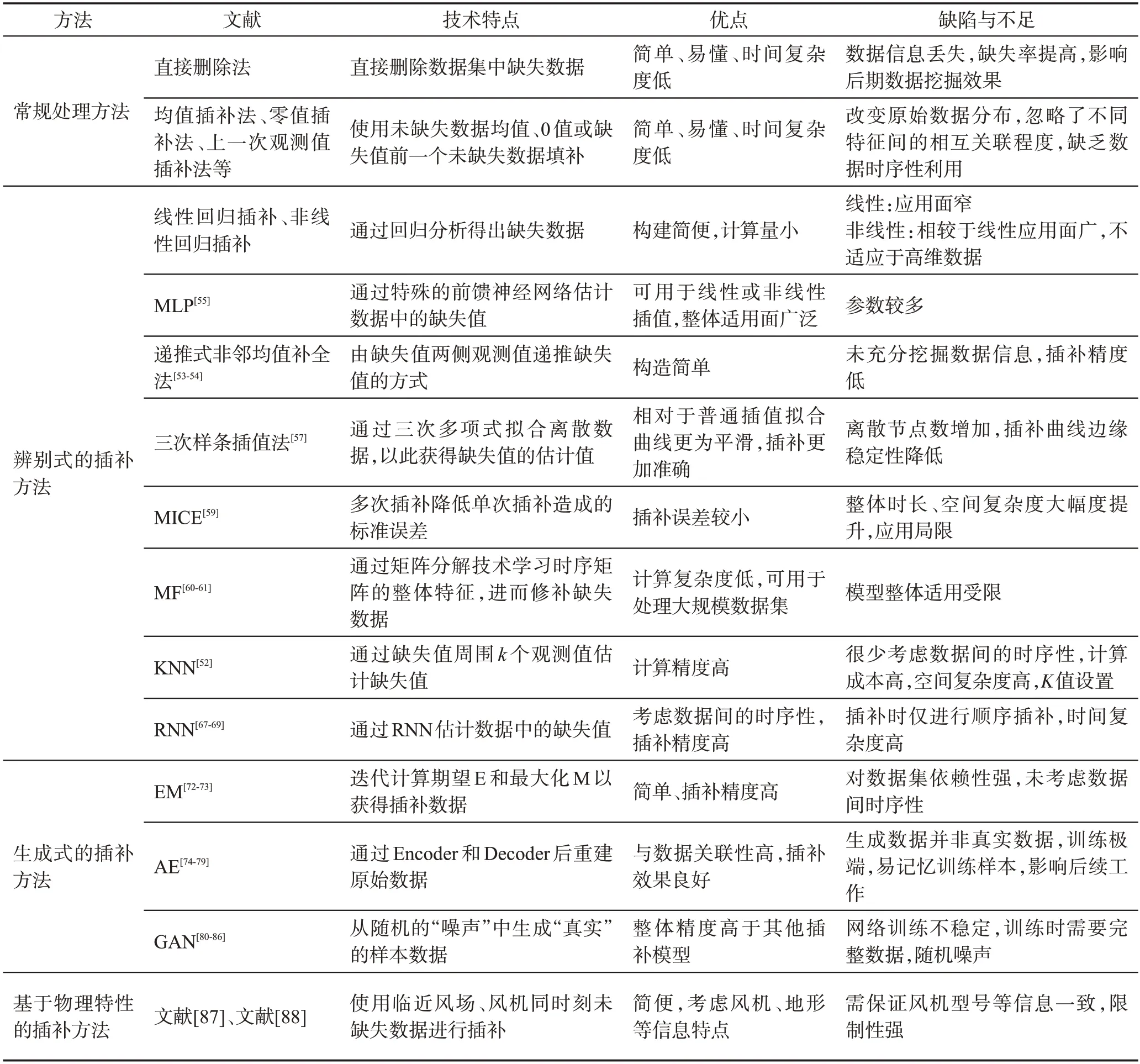
表2 风电机组缺失值插补方法对比Table 2 Comparison of missing value interpolation methods for wind turbines
(1)特有领域模型应用:近些年基于机器学习、深度学习插补模型层出不穷,但大多针对时序数据这一广泛领域中。不同数据间具有较大的差异性,针对不同数据特点进行的多变量插补模型迁移是未来工作中应当关注的一个问题。
(2)非固定时延问题:近年来基于VAE 和GAN的生成模型成为时序数据插补乃至图像、文本等领域的热点方法,与图像插补、文本填充等领域不同的是,时序数据插补时数据间所具有非固定时延问题,即数据缺失后导致数据时延增大。如文献[73]中研究所述,针对不同技术特点,如何完善模型不足,充分挖掘数据间时序性、数据分布及多变量相关性,提高模型插补效果和降低模型计算时长将是未来关注的另一个问题。
3 风电输出功率预测方法
可靠的风电输出功率预测可以大大降低这种不确定性,增强电力系统运行的稳定性及提高经济可行性。根据预测时长不同可划分为超短期预测[89]、短期预测[90]、中期预测[91]和长期预测[92]。具体时长和作用如图3 所示。不同预测方法根据预测值形式的不同分为确定性预测和概率性预测。在不确定的市场环境中,单一依赖确定性预测结果远远不够,而概率性预测通过调整模型初始化、改变模型结构和使用多种模型结合的三种方式结合NWP(numerical weather prediction)数据,给定预测结果的概率分布特征[93],进一步缩小预测误差,但所消耗的计算资源随之升高[94]。根据国家《风电功率预测功能规范》[95]所示,确定性预测通常采用均方根误差(root mean square error,RMSE)、MAE、最大误差(σ)和相关性系数(R)等进行衡量;概率性预测则采用可靠性(reliability)和锐度(sharpness)[96]等进行模型评价。本章对现有模型方法进行分析总结,并对目前研究中存在的挑战及未来可能的发展方向进行介绍。

图3 风电功率预测分类Fig.3 Classification of wind power forecasting
3.1 物理模型
物理模型是指根据数值天气预报(numerical weather prediction,NWP)数据,用物理方法计算风电场输出功率的模型。该模型也是目前研究较为成熟、深受人们认可的一种方法[97],通过NWP 数据模拟风电场区域内地形变化等,以预测该电场输出功率[98-99]。特别是在中期预测时,NWP 是提高预测精准度的首要环节[100]。
物理模型对气象、地形等数据依赖性较强、抗干扰性和可移植性差[101],同时高精度预测的计算复杂度和时间复杂度高。随着时长增加其预测精准度下降,导致单一物理模型的短期风电功率预测并不可靠[102],因此添加高精度NWP 数据作为模型输入,可进一步提高模型的预测准确性[103]。
3.2 统计模型
统计方法通过已有的历史数据和风电功率数据间的映射关系来建立预测模型[104]。统计模型可分为传统统计模型、时间序列模型、其他机器学习模型及深度学习模型。
3.2.1 传统统计模型
持续法作为最为经典的传统统计方法,将当前时刻的风电功率值作为未来时刻的预测值使用[105],这种方法虽然简单,但仅限于超短期预测使用,因此该方法通常作为基准模型进行使用,而非单独预测模型[94]。
3.2.2 时间序列模型
时间序列模型通过分析历史数据信息来预测未来数据,常用的时间序列模型有自回归模型(autoregressive,AR)、滑动平均模型(moving average,MA)、自回归滑动平均模型(autoregression moving average,ARMA)、自回归差分滑动平均模型(autoregressive integrated moving average,ARIMA)等。
AR 模型是处理数据内部关联的模型,其认为观测点后某一(段)时刻的值由该点前若干时刻观测值进行描述,即观测点xt值由前p个观测值与一个误差项构成,如式(1)所示:
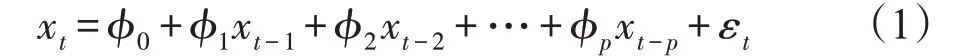
其中,ϕ0,ϕ1,…,ϕp为回归系数,εt为白噪声序列。
Poggi 等[106]使用AR 模型进行风速的预测和模拟。ARMA 模型由AR 和MA 两部分构成,结合了AR 和MA 的优点,相较于AR 模型更为常用。ARMA模型中xt的取值取决于过去p个观测点值与过去q个随机干扰项构成,具体如式(2)所示:

其中,θ1,θ2,…,θq为干扰项系数。
文献[107-109]采用ARMA进行风电功率数据预测,取得良好效果。文献[110]采用基于时间序列分析的风电场风速预测模型进行风速预测。文献[111]将校正后的ARMA 模型用于风电功率预测,结果表明该模型显著提高了中短期风电功率预测精度。AR、ARMA模型适用于平稳数据中,非平稳数据的使用将造成较大的误差。ARIMA模型在ARMA模型的基础上结合差分运算,将非平稳数据转换为平稳数据。因此,ARIMA 模型的应用更为广泛。为了提高模型的整体预测效果,研究人员还在ARIMA的基础上研究出许多组合预测模型,将在3.3节进行介绍。
时间序列模型仅分析了时序数据变量的潜在关系,很难用于挖掘数据间的非线性关系。因此这类模型仅适用于静态数据分析,这是此类模型的一个明显缺陷。同时伴随着时间序列数据复杂度的增加,单一时间序列分析模型对数据间特征提取效果不足以满足预测精度需要。
3.2.3 其他机器学习模型
机器学习模型作为人工智能领域研究的一个分支,模型可以根据给定的数据自适应学习做出决策并预测新的或未来一定时期的数据[112]。常见的回归模型、SVM、随机森林(random forest,RF)[113]、贝叶斯加性回归树(Bayesian additive regression trees,BART)、KNN 等机器学习算法广泛应用于风电输出功率预测、风速预测及其相关领域。
SVM被广泛应用于风速[114]、风电预测[115]领域,针对风电数据特点,后续研究人员在SVM 模型基础上进行改进,提出PSVM(piecewise support vector machine)[116]、LSSVM(least squares support vector machine)[117]等模型,这些模型进一步提升了SVM 模型的鲁棒性,提高风电输出功率预测精度。此外,基于SVM、PSVM、LSSVM等模型的组合预测模型相应提出。基于SVM的预测模型建立在严格的数学基础之上,具有高维计算速度快、不易陷入局部最优解等优点。但这类方法的效果与核函数及参数的选取紧密相关,这一点对使用者经验具有较强的依赖性。
由于RF 具有的简单性和多样性特点,被广泛应用于风电输出功率预测及相关领域。随机森林预测原理如图4所示。
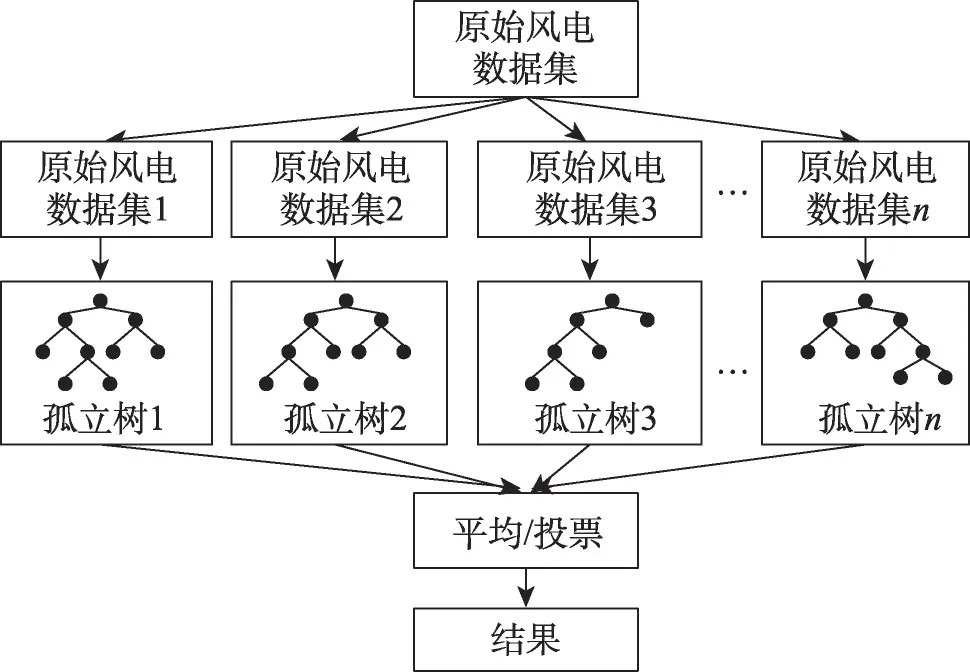
图4 RF预测原理Fig.4 Principles of RF prediction
Lahouar 等[118]采用RF 提前预测一小时的风电输出功率,相较于其他经典的机器学习方法不需要调整和优化;Shi等[119]提出了一种基于两阶段特征选择和决策树重组的RF模型,取代了训练样本和特征变量的无监督双随机抽样过程,进一步提高了模型的预测精度、效率及鲁棒性;文献[120]将RF 算法与决策树进行对比。此外,Wang 等[121]采用RF 算法进行风速输入特征选取,进一步简化风速预测模型结构并降低模型训练时间,从而提高了模型的准确性和泛化能力。整体来看,RF 算法适用于海量数据集分析,相较于人工神经网络(artificial neural network,ANN)和SVM 等算法具有较高的准确率和计算速度;在某些噪声较大的分类和回归问题上会出现过拟合现象,同时当训练数据少于分类类别时效果较差。
BART是一种基于贝叶斯回归树的方法,它是单个树模型的平均值[122]。Chen等[123]提出GKGPR(composite kernel methods based on Gaussian process regression)模型。该模型结合高斯回归过程和BART,改善现有BART 模型预测耗时问题。为更好地验证BART 模型效果,文献[124]对BART、GLM(generalized linear model)、GAM(generalized additive model)、RF 等模型进行对比分析。相较于其他机器学习算法,BART 方法预测精度高且不易出现过拟合现象,但预测所需时间较长,这并不利于实时预测需要。
综上所述,基于机器学习的预测方法可以根据数据自适应学习数据特点,相较于物理模型、传统统计模型和时间序列模型具有较高的预测精度,但该类模型对于数据集大小具有相应的要求,易造成过拟合现象。
3.2.4 深度学习模型
随着深度学习的快速发展,人工智能技术在语音识别、计算机视觉等领域广泛应用,同时相关技术也被应用于风电功率预测领域[125]。基于深度学习的预测模型由最初的反向传播网络(back propagation,BP)、RNN、CNN等单一模型预测到基于RNN等模型改进的模型进行预测。随着生成式模型的快速发展,基于AE、注意力机制(attention)[126]等模型解决了循环神经网络中递归计算无法并行的问题,同时减少了由于长期依赖性而导致的性能下降问题。此外,GAN网络作为生成式模型中的一大代表,也被广泛用于风电等时序数据预测领域。
单一的BP、RNN等模型是先前预测模型研究中的重点,如主成分分析(principal component analysis,PCA)与BP 相结合的风电功率预测模型[127]、结合滑动窗口的LSTM 预测模型[128]、CNN 进行特征提取的预测模型[129]及小波神经网络(wavelet neural network,WNN)预测模型[130]等。这些模型相较于其他机器学习模型具有较高的预测准确率,但仍存在一些问题。
人们普遍认为RNN的模型效果较差的原因是模型训练和推理时间长以及训练困难[131]。因此,在RNN、CNN的基础上进行改进,并基于RNN、CNN等单一模型构建深度学习框架。LSTM等RNN模型由于梯度消失问题的存在,预测过程中无法捕捉到极长时期的相关性。LSTNet[132]模型中提出RNN-skip结构用于解决上述问题,并将该模型用于太阳能发电等时间序列数据预测中,证明该模型的有效性。文献[133]提出一种以RNN 为基础的DeepState 时间序列预测模型,相对于DeepAR 模型[134],在训练及预测阶段不需要输入上一时刻的真实值或预测值,以解决DeepAR 模型训练和预测不一致的问题。目前在时序数据预测领域中,基于RNN 模型占有极其重要位置。但在最近的一些实验研究中发现,一些简单的CNN模型在不同的序列建模任务中比循环体系结构(如LSTM)更有效,如TCN(temporal convolutional network)[135-136]、基于残差的CNN模型[137]等。但是上述预测模型中大多数仍为单步超前预测,此类模型预测结果不足以支撑电力调度规划和运行,此外极个别的多步风电功率预测模型仍存在忽略不同预测任务间的相关性问题。同时,现有预测中常采用NWP 数据作为输入进行预测,而常规模型无法很好地对NWP数据中多元数据的长期依赖性很好地提取。AGRU(attention-based gated recurrent unit)[138]模型、MSTAN(multi-source and temporal attention network)[139]模型对上述不足进行了完善,但是导致空间复杂度等新型问题出现。
AE 由编码器和解码器两部分构成,其将原始数据压缩成潜在空间特征,然后经过解码器进行重构输出。近年来基于AE 及其改进模型被广泛应用于风电功率预测领域(AE 结构示意如图5 所示)。如SAE-BP[140]将SAE(stacked auto-encoders)与BP 结合进行风电功率预测,使得模型相对于BP等模型更稳定;SDAE(stacked denoising auto-encoders)[141]能够模拟给定风场间的空间相关性和相互依赖性,提高NWP 精度以进行风电功率预测等。AE 作为无监督模型中的一种,可以在数据提取过程中过滤噪声。文献[142]对现有基于Attention机制的预测模型进行对比分析,证明基于Attention 机制的模型在一定程度上预测效果优于传统模型。但这并不能完全说明基于Attention机制的模型一定会比LSTM等RNN模型效果好,如attention-LSTM(在注意力层上叠加一个LSTM层)模型的预测效果低于vanilla LSTM。从上述文献中可以看出,单一结合Attention 机制与RNN等网络的预测方法效果并不一定会优于传统模型,同时也会导致新的问题的出现。现有基于Attention 模型预测效果多数优于RNN 等传统模型,降低了该类模型中CNN 特征提取时的内存消耗,但存在权重冗余现象。
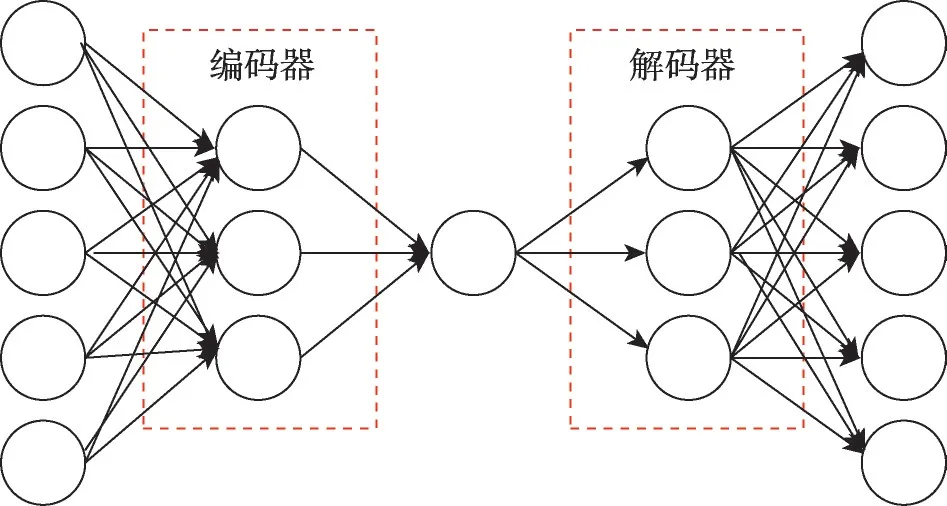
图5 AE结构示意图Fig.5 Schematic of AE structure
近些年来,GAN受到广泛关注,其中生成器将噪声变量映射至多层感知机网络,使生成的数据尽可能接近训练样本的分布;辨别器再确定输入数据是来自训练样本还是生成模型(GAN结构示意图如图6所示)。文献[143]分别采用GAN进行确定性和概率性风电输出功率预测,以证明最新发展的GAN 网络可用于风电输出功率等时序数据预测中。基于GAN网络的改进的RAC-GAN[144]、PG-GAN[145]应用于风电预测领域,并取得良好的效果。基于GAN 网络的模型为半监督模型,不需要人工大量标注数据。即使没有任何标签,其也可以根据历史数据对概率分布进行建模。但从整体来看,该类模型计算效率较低且无法描述输入数据特征。
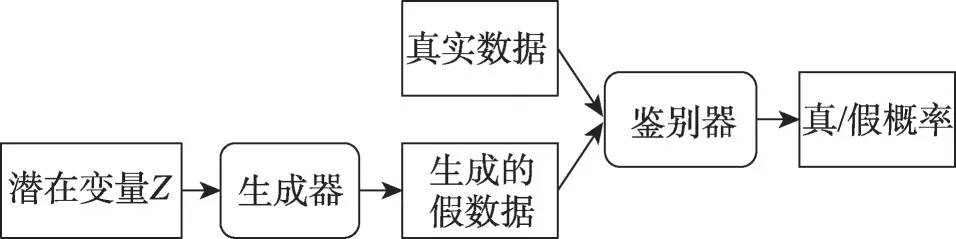
图6 GAN结构示意图Fig.6 Schematic of GAN structure
深度学习模型相较于物理模型、传统统计模型、时间序列模型能够更好地挖掘数据间信息,提高整体的预测精度。深度学习预测模型中BP、RNN、CNN等模型能够较好地提取数据内部的时序特性或短时信息;基于RNN、CNN 等改进的LSTNet(long and short-term time-series network)等模型针对RNN等模型的局限进行改进,虽提高模型的检测效果,但仍引进模型过于复杂等新型问题;基于AE、GAN 等模型改进的生成式预测模型进一步挖掘数据的隐特征信息。这些模型具有较强的学习能力和鲁棒性,但随着数据量的增大,特别是模型过于复杂时,对于计算资源等具有较大的要求,同时深度学习模型的可解释性仍是目前研究界的一大难点。
3.3 组合模型
由于风电功率具有高随机性和波动性特点,单一模型的预测效果往往无法满足实际需要[146]。近些年来,结合多个单一模型优点的组合模型研究成为风电功率预测研究中一个热门方向。目前,组合预测模型可大致分为四类[147],即基于多模型加权的组合预测方法、基于数据分解的组合预测方法、基于优化技术的组合预测方法和基于误差修正的组合预测方法。
3.3.1 基于多模型加权的组合预测方法
基于多模型加权的组合预测方法通过多个子模型分别进行预测,并将结果进行加权输出(如图7 所示),如LSSVM 与RBFNN(radial basis function neural network)加权组合预测方法[148],SVM与LSTM、ARIMA等模型加权组合预测方法[149],极限学习机、双向长短期记忆网络(bi-directional long short-term memory,BiLSTM)和Elman 网络加权组合预测方法[150]等。这些方法将多个单一基础模型进行组合,以提高模型的预测结果。为证明加权组合模型预测效果优于单一模型,文献[151]采用ARMA、径向基模型、SVM模型等与组合模型进行对比,以验证组合模型的优异性和准确性。
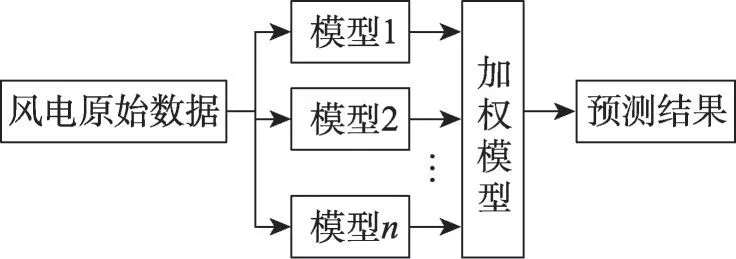
图7 基于多模型加权的组合预测方法示意图Fig.7 Schematic diagram of combined forecasting method based on multi-model weighting
此外,模型内部结构优化及多特征预测方式也可以进一步提高整体效果。文献[152]利用非参数下限估计框架结合LSTM(长短期记忆网络)进行短期风电功率预测,结果显示该模型性能优于典型的RNN(循环神经网络)。多特征预测通过对原始数据中某些特征数据进行预测,并将该预测值作为补充数据输入风电预测模型中,以提高风电预测模型的预测效果和鲁棒性。如文献[153]考虑NWP 数据不确定性,采用DBN(deep belief network)进行短期风速数据预测,并将风速预测值作为补充数据采用随机森林算法进行预测,结合加权投票法(weighted voting approach)进行模型更新。
基于多模型加权的组合预测方法通过权重更新器,可自动调整每个子模型权重。其灵活性、适应性、预测精度较高,同时其计算效率低、应用场景较窄。
3.3.2 基于数据预处理的组合预测方法
利用数据预处理技术将原始风电数据分解成多个平稳的子序列,并采用模型对子序列分别进行预测的组合预测方法如图8所示。

图8 基于数据预处理的组合预测方法示意图Fig.8 Schematic diagram of combined forecasting method based on data preprocessing
此类方法结合信号分解思想,采用经验模式分解(empirical mode decomposition,EMD)、变分模式分解(variational modal decomposition,VMD)等数据分解技术对原始风电(或风速)数据进行分解,并采用预测模型对分解后的数据分别进行预测。如文献[15]提出基于EMD和人工神经网络的混合方法用于风力预测。文献[154]提出使用改进的VMD 来分解风电数据,并采用LSTM进行预测。但上述文献均未考虑风速等数据的季节性影响,基于此,文献[155]提出LSTM-SARIMA(LSTM-seasonal autoregressive integrated moving average)超短期风电功率预测模型,在分解过程中考虑气象和季节因素影响,大幅度提高模型的预测精度。
基于数据预处理的组合预测方法相较于其他组合预测方法结构更为简单、计算效率高,易迁移至点预测、多步预测、日前预测等场景,但整体预测精度有限,缺乏对预测误差的理论分析。
3.3.3 基于优化技术的组合预测方法
基于优化技术的组合预测方法通过采用优化技术优化模型参数,以此提高模型的预测效果(如图9所示)。基于遗传算法(genetic algorithm,GA)的WSVM-GA[156]模型、基于引力搜索算法(gravitational search algorithm,GSA)的LSSVM-GSA[157]模型等结合优化算法选取最优参数,以提高模型预测精度。
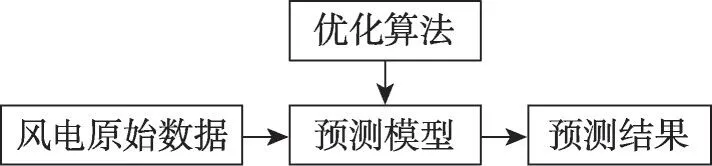
图9 基于优化技术的组合预测方法示意图Fig.9 Schematic diagram of combined forecasting method based on optimization technique
传统优化算法由于自身局限性等因素的影响,无法满足高水准参数优化需求,基于传统优化算法改进的优化技术也被广泛应用于风电预测领域。如文献[158]提出一种改进的果蝇算法优化SVM,并用于短期预测。文献[159]采用贫富优化算法对离群鲁棒极限学习机的参数进行优化,提高模型的泛化能力并用于风电功率预测。文献[160]提出一种混合改进布谷鸟搜索算法来优化支持向量机的超参数,用于短期风电功率预测。
大多数深度学习预测模型训练受参数初始化影响,初始化策略基于在神经网络初始化时实现一些很好的性质,基于优化技术的组合预测方法成为近些年研究的一大重点。相较于传统优化技术应用受限问题,GA等智能优化技术针对数据的不确定性也有很强的适应能力,有些能够得到更快的收敛率和更好的泛化误差。但相较于传统优化技术,此类理论分析不够完善,且存在求解无法保证最优解的问题。
3.3.4 基于误差修正的组合预测方法
基于误差修正的组合预测方法是利用数据后期处理技术的组合方法来减少预测方法中误差所带来的负面影响的组合预测算法(如图10所示)。

图10 基于误差修正的组合预测方法示意图Fig.10 Schematic diagram of combined forecasting method based on error correction
该类方法通常采用统计方法对误差进行估计,以提高模型的整体预测效果。如文献[161]采用马尔可夫对模糊神经网络(fuzzy neural networks,FNN)模型预测结果进行修正;文献[162]在高斯过程中使用时空局部滑动窗口技术来检查预测误差,进而提高预测效果等。此外,机器学习方法也常用于误差估计中。文献[163]采用SVM和Elman网络进行预测和误差模型的构建;文献[164]采用基于RBF的LSSVM进行误差修正。与未修正误差的预测模型相比,修正后的预测模型预测精度明显提高。
基于误差修正的组合预测方法量化模型误差大小和数据噪声的不确定性,拥有较高预测精度,可提供预测误差的统计分析。但相较于其他组合算法来看,整体计算效率较低。
3.4 多层级预测研究
在工业界和学术界的时间序列预测数据中,通常具有分层结构,其中每个上层时间序列是通过对对应的下层时间序列求和进行计算的,即上层时序数据等于下层时序数据之和[165]。在过去几十年中,共有三种协调方法用以确保预测的连贯性,即自下而上、自上而下和两者结合的中间向两边的方式。每个方法都侧重于不同的聚合级别以产生预测,如自下而上的方法首先对底层时间序列进行预测,并根据聚合方式来获得高层次时间序列预测值。该方法优点是几乎不丢失信息,但往往会随着时间序列级别的上升而积累预测误差。自上而下的方法首先对顶层时间序列进行预测,并根据较低层次的历史比例进行预测。该方法在底层节点预测存在误差时是稳定的,但往往无法利用较低级别时间序列的详细信息。中间向两边的方法首先对中间某层时间序列进行预测,并结合自上而下和自下而上的方法完成剩余层级的预测。MA(moving average)等方法广泛应用于多层时序数据预测中,但其准确率低,同时当其受到时间变化或任何突然变化的影响,它们可能无法很好地执行[166]。
上述方法通常采用基础预测和根据层次结构协调预测两部分进行,预测效果不佳。针对这一问题,文献[166]提出一种结构化的正则化方法,同时进行上述两个阶段以产生更好的时间序列预测。该方法相较于传统机器学习方法,更易于扩展至ANN 模型中。与此不同的是,文献[167]提出一种新的支持向量回归方法来处理多层时间序列预测,其通过两种变体进行跨层级汇集信息,防止底层预测相对于上层序列存在很大偏差。为降低低层次预测误差累计问题,文献[168]使用DLSTM-AE(deep long short-term memory model in auto-encoder)对底层时间序列数据进行训练和预测,并采用迁移学习对上层结构时间序列数据进行同步训练,以估计目标预测。该方法相对于MA等静态方法考虑更多有用信息,并结合迁移学习降低模型训练及预测所需时间,显著提高模型的预测效率。但在现有的大多数方法中仅可进行点预测,而不是概率性预测。在实践中,概率性预测能帮助运维人员更好地制定决策和风险管理。针对这一问题,文献[169]提出一种多层次概率性预测方法,采用end-to-end模型同时进行基础预测和层次协调。相对来说,该方法更适用于高斯分布数据,对于非高斯分布数据,作者并未进行相应的探讨和研究。整体来看,此类文献或对三种协调技术进行优化,或提高模型预测精度以降低预测误差,或将前者组合,提高基础模型预测效果的同时,充分提取多层次时序数据间的层次关系,以提高整体效果。
3.5 自适应风电预测系统研究
自适应为软件系统配备一个反馈回路,使得系统可以自动执行原本需要由操作人员执行的任务。近些年来,机器学习成为支持自适应的流行方法。但针对机器学习技术处理自适应中的几个方面,仍面临着一些问题。
Gheibi 等[170]介绍了在自适应系统中机器学习解决的问题、自适应学习时考虑的关键工程及自适应系统中使用机器学习所面临的挑战。自适应系统中机器学习问题包含适应问题和学习问题:适应问题包括质量提高、平衡质量与资源、平衡质量与成本、改进资源分配和防御网络威胁;机器学习解决的具体问题包括更新/更改适应规则/策略、预测/分析资源使用、保持运行时模型最新、减少大适应空间、检测/预测异常、收集不可用的先验知识。
风电预测系统中如何保持运行时模型最新是学习问题的一大重点,而终身机器学习(lifelong machine learning)是机器学习系统学习未提前定义的新任务的能力[171],但目前终身机器学习存在处理时灾难性遗忘和机器学习管道机制规范不足的问题,即学习新信息时丢失以前学习到的信息和模型训练到部署时性能显著下降问题。Chen[172]使用所有可用数据在每个循环中重新训练一个新模型,以及使用新到达的数据样本重新训练现有模型两种方法来处理自适应学习中的概念漂移。Chen等[173]利用自适应多学习器,动态选择最佳模型进行预测,并在云环境中进行评估。针对数据中存在的概念漂移和协变量漂移问题,Gheibi 等[174]提出一种新的自适应方法,以更新自适应系统的学习模型。
整体来看,目前自适应系统内机器学习算法研究以监督学习方式为主,无监督学习、对抗学习及主动学习方式研究较少。同时,学术界与工业界对于研究的认可存在差异,学术界倾向于最新的研究发现,而工业界更侧重于成熟的研究,这也或将是目前基于自适应预测系统研究不成熟的问题之一。
3.6 风电预测存在的问题与挑战
现有预测方法对比效果如表3 所示。针对目前研究中不同方法及应用存在的问题,大致分为以下几点:

表3 现有风电功率预测方法对比Table 3 Comparison of existing wind power forecasting methods
(1)NWP数据精度提升问题:针对3.1节中,NWP数据中存有误差,使得后期风电功率预测时存在一定程度的误差,因此如何通过提升原始NWP 数据精度以提高风电预测模型精度将是未来研究中的一个重点及难点[175]。
(2)组合预测模型缺陷完善问题:针对3.3 节中,多个单一模型组合构成的组合模型在一定程度上解决了单一模型自身存在的弊端,使得整体风电功率预测精度超过或等于最优单一模型预测精度。但上述四种不同类型的组合模型具有不同的优缺点,针对实际问题扬长补短是今后研究中着重考虑的问题之一[176-177]。
(3)风电功率爬坡事件预测问题:为解决风电功率爬坡事件并网时对电网产生损害情况,提前对风电输出功率爬坡事件的预测是必要的[178]。同时,将储能系统研究与风电预测相结合的方式可以减缓风电爬坡事件带来的影响,目前虽有些许相关研究,但整体来看仍有一定进步空间[179]。
(4)模型可解释性及子任务协同问题:目前研究中,大多数文献将预测模型认定为黑盒问题,并未深入研究模型内部参数与实际预测值精度间相关性;同时针对3.4节分析,多层级预测等预测子任务间协同训练也是目前研究中亟待解决的重要问题之一[180]。
(5)模型融合问题:现有基于时间序列分析的深度学习框架中,许多通过些许修改以用于异常值检测、插值等领域。现有研究中,异常检测、插值和预测等模型研究通常是相互独立的,大多针对数据本身研究,这也或将成为导致同时进行异常值检测、插值及预测的模型框架目前研究较少的主要原因。采用模型融合思想,使模型可同时进行数据清洗和预测将是未来研究的一个方向[181]。
(6)基于模型的自适应风电预测系统研究问题:常规预测系统仍为目前风电功率预测系统研究中的研究重点,该类系统仍停留在以代码为中心的自适应系统或未添加自适应性系统的情况下。如3.5 节所述,基于机器学习的自适应系统在发生变化时应当具有自动进行规划的能力[182],使得预测系统具有自主规划、及时响应特点的研究是未来发展的一个重点方向。
4 结束语
风电数据存在较强的随机性和不确定性,使得高精准度的风电功率预测模型难以构建。针对风电数据采集过程中存在的异常及缺失数据,本文对现有研究中的异常值检测技术、缺失值插补技术和风电功率预测技术的研究现状根据模型特点进行划分和分析,并对未来技术进行展望。由技术角度发现,现有模型朝着组合化、复杂化发展。希望本综述对风电等时序数据的异常检测、缺失插补及数据预测领域的研究提供一定的参考价值,可以为相应模型的深入研究提供一定的帮助。

