多视角层次聚类下的无线网络入侵检测算法

董新玉，解 滨,3+，赵旭升，高新宝

1.河北师范大学 计算机与网络空间安全学院，石家庄 050024

2.河北师范大学 河北省网络与信息安全重点实验室，石家庄 050024

3.河北师范大学 供应链大数据分析与数据安全河北省工程研究中心，石家庄 050024

无线局域网技术和移动通信设备的迅猛发展使得WiFi 网络环境逐渐普及并融入人们的生活，这同时也使得WiFi成为网络攻击的目标。“蹭网”“无线钓鱼”等无线网络犯罪事件时有发生，引发了个人数据被泄露、篡改等信息安全隐患，甚至导致大的经济损失[1]。网络攻击行为的不断演化和升级使得无线网络环境下的网络安全问题愈发严峻，成为信息安全的新困局。

网络入侵检测是目前应用最广泛也最有效的网络安全主动防御方法，入侵检测技术作为一种重要的动态安全技术，很好地弥补了静态安全技术的不足。入侵检测技术主要分为两类：误用入侵检测和异常入侵检测[2]。误用入侵检测是指通过建立已知入侵行为特征数据库，利用该数据库对网络中的数据流量进行实时监控，以模式匹配的方式判断网络行为及其变种行为是否异常，当数据流量特征与特征数据库中的任何一条规则有交集，即可判定为入侵行为。误用入侵检测技术依赖于已知入侵行为特征库，对于已知攻击类型的入侵行为能够快速准确地检测到并作出类别判断，但是该技术无法检测到未知攻击类型的网络入侵行为。异常入侵检测技术恰好能解决这一问题，其通过建立正常行为特征数据库来实现入侵检测目的，当网络数据行为特征不符合正常行为特征数据库规则时，即判定该行为为网络入侵行为。该技术可以检测到未知攻击类型的入侵行为，但是检测过程中误检率和漏检率较高。随着网络入侵行为的不断多样化和复杂化，基于异常检测技术的网络入侵检测系统更能适应多变的网络环境，使之成为当下较为流行的入侵检测机制。

基于有监督异常检测的网络入侵检测系统，在实际应用过程中需要通过对大量正常行为数据进行标记，建立正常行为特征库。但是，在现实网络环境中想要获取纯净准确的正常行为数据集是很困难的，并且代价很大。为解决这个问题，人们提出了无监督异常检测方法[3]，该方法不依赖于已标记的数据，不需要人工或者其他方法对训练数据集进行标记和分类，大大提高了检测系统的实用性。基于无监督异常检测的网络入侵检测算法遵循以下两个假设：（1）网络数据集中正常行为数据量远远多于入侵行为数据量；（2）网络数据集中正常行为数据特征与入侵行为数据特征之间存在较大差异。

随着无监督异常检测得到研究者关注，一系列卓有成效的数据挖掘和机器学习中的方法被应用于无监督异常检测。如Jiang和Song等人[4]提出了一种新的无监督聚类检测方法（clustering-based method for unsupervised intrusion detection，CBUID），该方法在标记簇时考虑了簇的偏离程度（deviation degree），并且在聚类时使用了INN（improved nearest neighbor）算法，该算法有效地提高了聚类的质量。刘卫国等人[5]提出了一种全部属性聚类和特征属性聚类相结合的无监督异常检测模型，该模型将数据集划分为不同的服务集，然后对每个服务集数据包进行全部属性聚类和部分相关属性聚类，取其中训练性能较优的方法建立对该服务的检测模型。周亚建等人[6]提出了一种基于改进的CURE（clustering using representative）聚类算法的无监督异常检测方法。在保证原有CURE聚类算法性能不变的条件下，通过对其进行合理的改进获得更加理想的簇，也为建立正常行为模型提供了更加纯净的正常行为数据。为减少由于异常值与正常值之间相互干扰而产生的漏报和误报，吴金娥等人[7]提出用反向K近邻算法对异常群数据进行反向过滤，将统计距离作为不同群数据间的相似性度量，算法有较高的异常检测率和良好的稳定性。

目前，这些无监督异常检测方法所使用的聚类或K 近邻算法在网络实时状况变更的情况下不能灵活控制聚类簇个数以适应多变复杂的无线网络环境[8]。并且，大多数算法采用欧式距离作为数据对象之间的相似性度量，而对于高维数据，使用余弦距离来刻画要比欧式距离更合适[9]。李飞江等人[10]提出的全粒度聚类算法采用余弦距离来刻画数据对象间的相似性，得到了较欧式距离更为合理准确的聚类结果。但是，该算法以将欧式空间网格化方式选取基准点，一方面影响余弦距离测量的内部基准点偏多，另一方面在笛卡尔坐标系下网格化选取的基准点数量较为庞大，复杂度较高。

本文提出一种以多视角方式选择基准点、结合层次聚类构造无监督无线网络入侵检测算法，在聚类过程中可通过调节层次聚类距离阈值来动态控制聚类簇个数，更能适应当下多变复杂的无线网络环境。同时，该算法引入多视角余弦距离作为层次聚类的距离度量方式，在衡量任意两个数据对象之间相似性时综合考虑各个视角下该数据对象间的相似性，使得数据对象之间的相似性度量更加合理和准确，从而提高入侵检测算法的检测率，降低误检率。对于离群数据点和任意簇下的数据对象，这种相似性度量方式要明显优于基于传统欧式距离的相似度量。本文实验选用公开无线网络数据集AWID，采用主成分分析法（principal component analysis，PCA）对实验数据进行降维处理，在一定程度上减小了数据特征规模，提高了算法的性能。实验结果表明，本文提出的基于多视角层次聚类的无线网络入侵检测算法较传统无线网络入侵检测算法在检测率、误检率和发现未知攻击类型等性能上均有显著提升。

1 基于多视角层次聚类的无线网络入侵检测

1.1 无线网络入侵检测过程概述

无线网络入侵检测过程[11]主要包括以下几个模块：（1）WiFi网络数据获取；（2）数据预处理；（3）分类器学习；（4）构建分类器；（5）无线网络数据检测；（6）响应机制。其中，模块（1）～（4）属于入侵检测学习阶段，模块（5）、模块（6）属于检测阶段。现实网络环境中一般通过无线网络监听设备来获取WiFi无线网络数据，获取后的无线网络数据经过预处理进入到分类器学习模块，通过训练大量无线网络数据构建能够判断网络数据行为的分类器。无线网络实时流量经检测模块的分析判断确定其行为类别，并适时启动入侵检测响应机制。检测过程如图1所示。

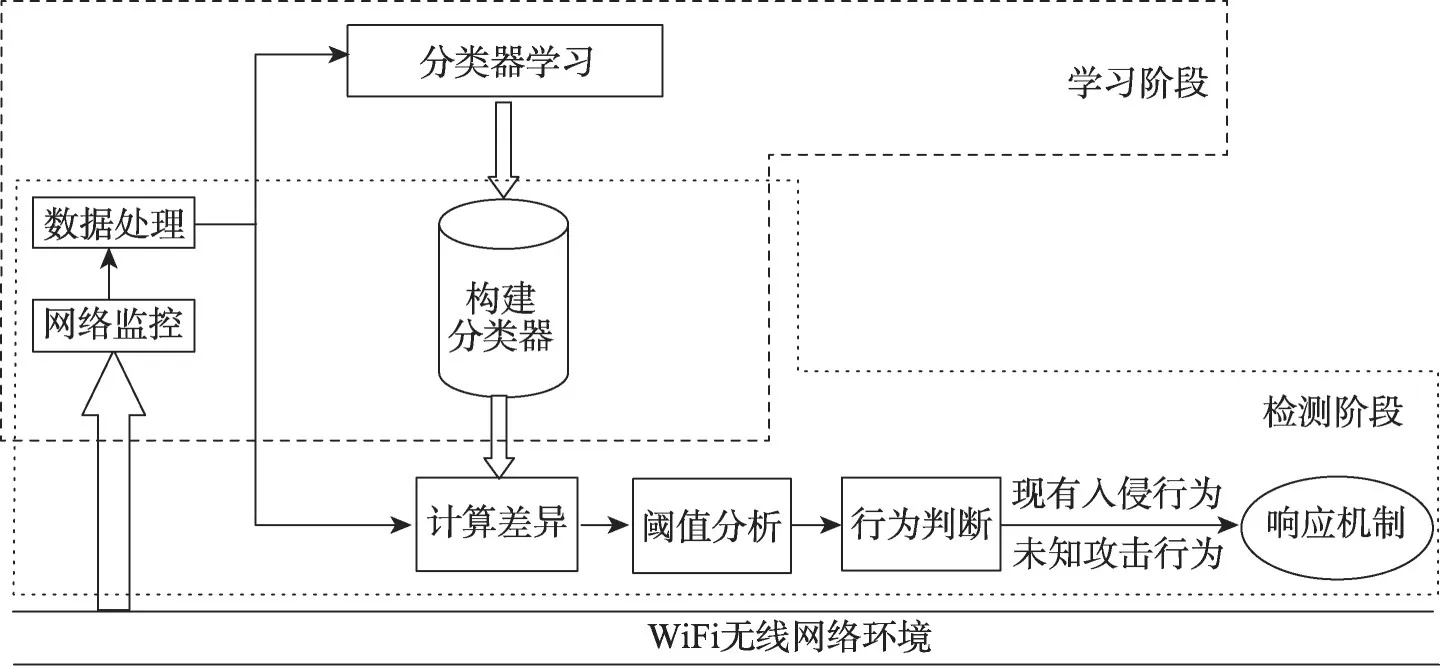
图1 无线网络入侵检测过程示意图Fig.1 Schematic diagram of wireless network intrusion detection process

传统的K-means聚类算法、KNN（K-nearest neighbor）分类算法等是构建分类器经典的算法。该类算法根据网络数据行为的差异对数据集进行分类学习，提取网络数据行为特征，构建数据分类器。数据分类器对任意实时网络数据流量进行特征提取和行为判断，从而实现对网络环境的实时监测功能。通常情况下，不同的检测系统会根据网络环境和网络状态的不同而设定合适的数据行为判定阈值。入侵检测过程中，检测系统会结合分类器分类情况和阈值的设定来输出数据行为的最终判定结果。随着无线网络入侵行为的不断多样化和复杂化，固定分类数量的K-means和KNN算法已经不能满足入侵检测系统的需要，在未知的无线网络环境下，入侵检测系统并不能提前获得网络数据行为的准确类别数，这一现象使得基于固定分类数量的K-means及KNN算法的数据分类器学习能力和分类性能大大降低。为降低固定分类个数K对分类器性能的影响，本文使用层次聚类算法构建分类器。层次聚类算法相较Kmeans及KNN算法在构建分类器过程中通过设置层次聚类距离阈值来灵活控制分类个数，使得分类结果更能符合当下无线网络环境实况。

1.2 层次聚类算法

层次聚类的主要思想[12]是在不同层次对数据集进行划分，分为“自底向上”的聚合策略和“自顶向下”的分拆策略两种形式。“自底向上”的策略，开始时把每一个原始数据看作一个单一的聚类簇，然后不断聚合小的聚类簇成为大的聚类簇。“自顶向下”的策略开始把所有数据看作一个聚类簇，通过不断分割大的聚类簇直到每一个单一的数据都被划分。结合无线网络数据集AWID 的数据特征，本文选用“自底向上”的层次聚类聚合策略，聚类终止条件是符合预设的距离阈值α或者达到预设的聚类簇个数k。层次聚类的关键是如何选择聚类簇之间的距离和如何确定聚类阈值α。聚类过程中，每个聚类簇是一个数据样本集合，计算聚类簇之间的距离时只需计算集合间的某种距离即可。如给定聚类簇Ci与Cj，可通过下面的式子来计算距离：

聚类簇之间的最小距离：

聚类簇之间的最大距离：

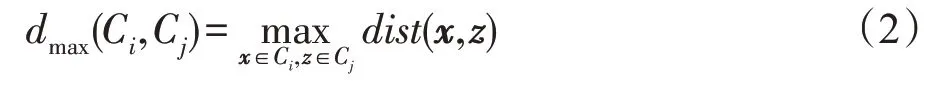
聚类簇之间的平均距离：

其中，|·|为集合的基数。

平均距离作为聚类簇之间的距离度量方式，综合衡量了聚类簇中所有数据对象对聚类簇之间距离的影响，更加适合对无线网络数据集的分类，增加聚类算法的鲁棒性。

图2为自底向上层次聚类示意图，横坐标代表网络数据集中的数据对象，编号为p1～p6，纵坐标为聚类簇之间的距离，聚类过程如图3所示。在层次聚类算法中，可根据提前设定好的距离阈值或者聚类簇个数终止聚类过程，得到相应的聚类结果。例如，设定距离阈值为0.118时（如图2虚线所示）可以得到如下所示的聚类结果：

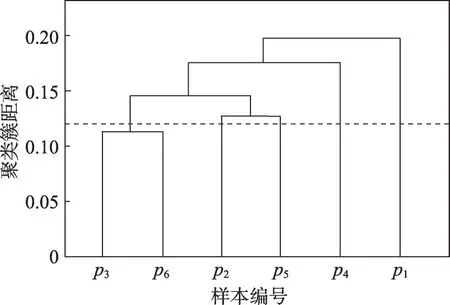
图2 层次聚类示意图Fig.2 Hierarchical clustering diagram

图3 层次聚类过程图Fig.3 Hierarchical clustering process diagram

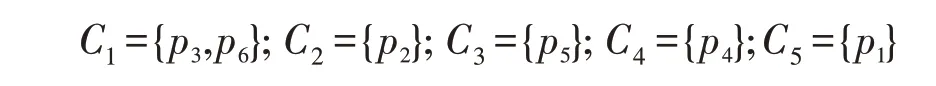
1.3 多视角相似性度量

层次聚类算法的最终目的是把给定的数据集进行分类，使得相似度高的数据对象在同一类中，差异较大的数据对象分布在距离较远的类中。欧式距离是聚类算法中常用的样本之间距离的度量方式，如式（4）所示，传统的K-means 聚类方法就是通过极小化每个样本到类中心的距离和来达到聚类的目的，表示为式（5），表1给出了本文需要用到的符号表达。

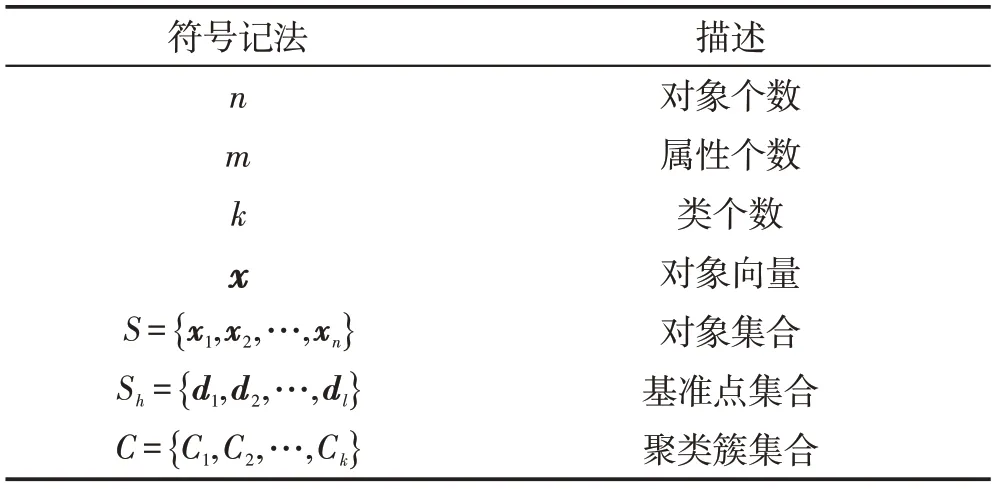
表1 层次聚类符号表达Table 1 Hierarchical clustering symbol expression

在样本之间相似度量方法中，欧式距离侧重于度量样本之间属性值的数值上的差异，余弦距离侧重于维度间取值方向的一致性，主要度量维度之间的差异，不注重数值上的差异。对于维度较高的无线网络数据来说，这两种传统的度量方式都存在局限性。本文将改进的余弦距离度量方式引入到无线网络数据的层次聚类算法中，在多视角下衡量无线网络数据对象之间的相似性，得到两个数据对象之间更加合理、真实的相似度，从而使得聚类结果更加理想。

基于余弦的距离可表示为：

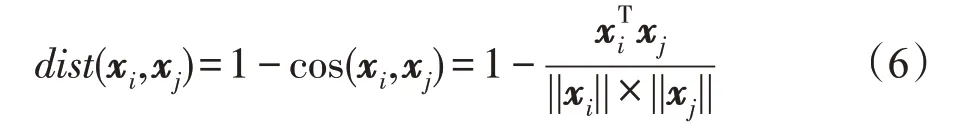
其中，cos(xi,xj)为数据xi和xj间的夹角余弦，用来衡量数据对象之间的相似度[10]。

从式（6）可以看出，余弦距离可以看作以原点作为视角来观测两个对象的夹角，因此，余弦距离也可以表示为：

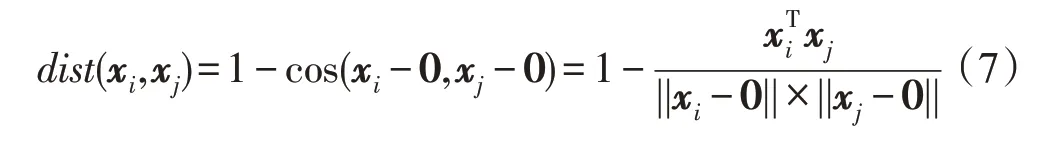
式（7）的这种计算方法只把0 作为基准点，两个对象之间的夹角也只是从原点来看的夹角，如图4（a）所示。但是对于同原点接近于一条直线的两个数据对象来说，以原点为唯一基准点的余弦距离度量就失去了效果，如图4（b）所示。因此，采用多个视角进行余弦距离度量将有效解决这一问题。

图4 以原点为视角观测数据间距离Fig.4 Measuring distance between data objects from origin view

引入非原点的第三个点dh作为基准点，数据xi和xj间的距离表示为：

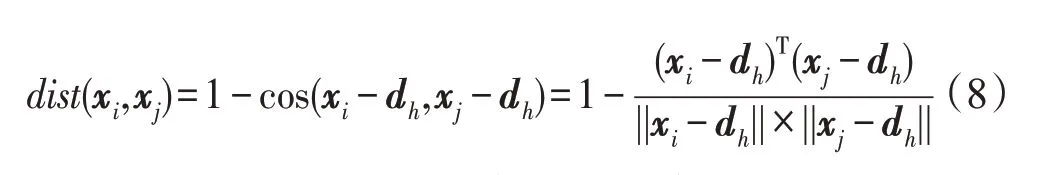
在度量两个数据对象之间相似度的时候，从基准点集合Sh中的每个点观察两个数据对象之间的夹角，也就是向量xi-dh和xj-dh之间的夹角。数据xi和xj间的距离可由多个基准点观察的余弦距离的平均值表示：

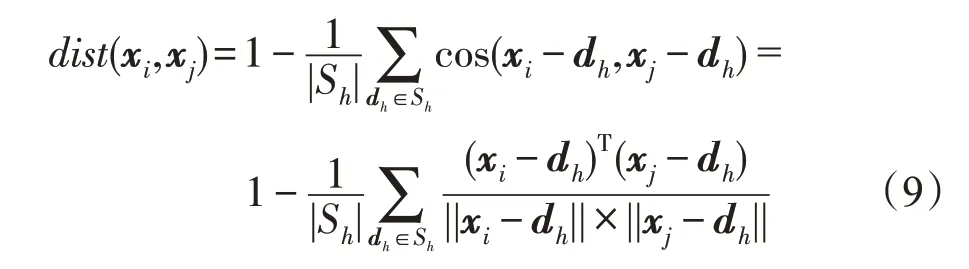
其中，|Sh|为基准点集Sh的基数。

文献[10]提出在全粒度下按照预设的取点步长在各个维度上依次选取基准点的方法，得到了较为理想的聚类结果。但是，该算法的基准点是通过空间网格点的方式选取的，使得基准点数据量庞大，导致算法的时间复杂度较高，同时也增加了很多降低余弦距离判断准确性的干扰基准点。为解决这一问题，本文采取多视角方法选取基准点，有效减小基准点集规模的同时，提高了聚类的准确度。多视角选取基准点的思想如下：

设A为n维空间中单位超立方体的外接超球面上的点，O为球心，当点A在单位超球面上按照球坐标等角度步长选取时，则在笛卡尔坐标系OX1X2…Xn中，点A的笛卡尔坐标(X1,X2,…,Xn)计算如下：

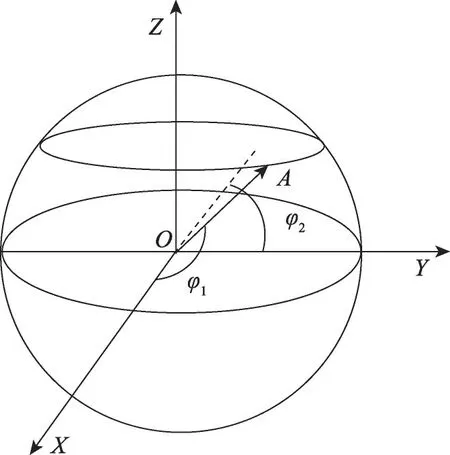
图5 三维空间任意基准点示意图Fig.5 Schematic diagram of arbitrary datum point in three-dimensional space

其中，n为空间维度，三维空间中n取值为3。由此可得，点A在空间直角坐标系中的坐标为(X,Y,Z)。

例如，三维空间中，选定N=3 时，多视角方法得到的基准点坐标如表2所示，图6为示意图。

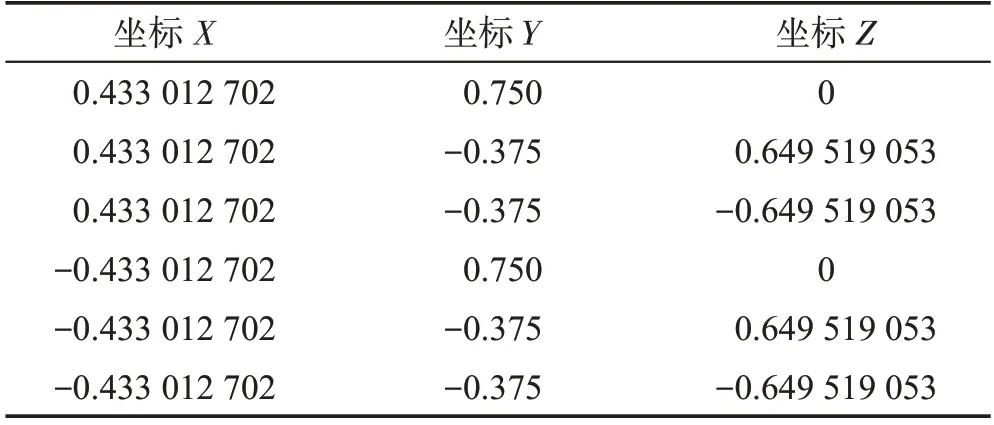
表2 六个基准点坐标Table 2 Coordinates of 6 datum points

图6 三维空间基准点集示意图Fig.6 Schematic diagram of three-dimensional space datum point set

在n维空间中，文献[10]的全粒度方法选取基准点的基准点集规模为(N-1)n，本文的多视角方法选取基准点的基准点集规模为N(N-1)n-2。当数据集维度增高时，基准点集规模会越来越大，对算法性能的影响也会随之变大，因此在高维数据集上减小基准点集的规模对于算法性能的提高至关重要。当N=3时，在不同维度下两种方法选取基准点个数对比结果如表3所示。

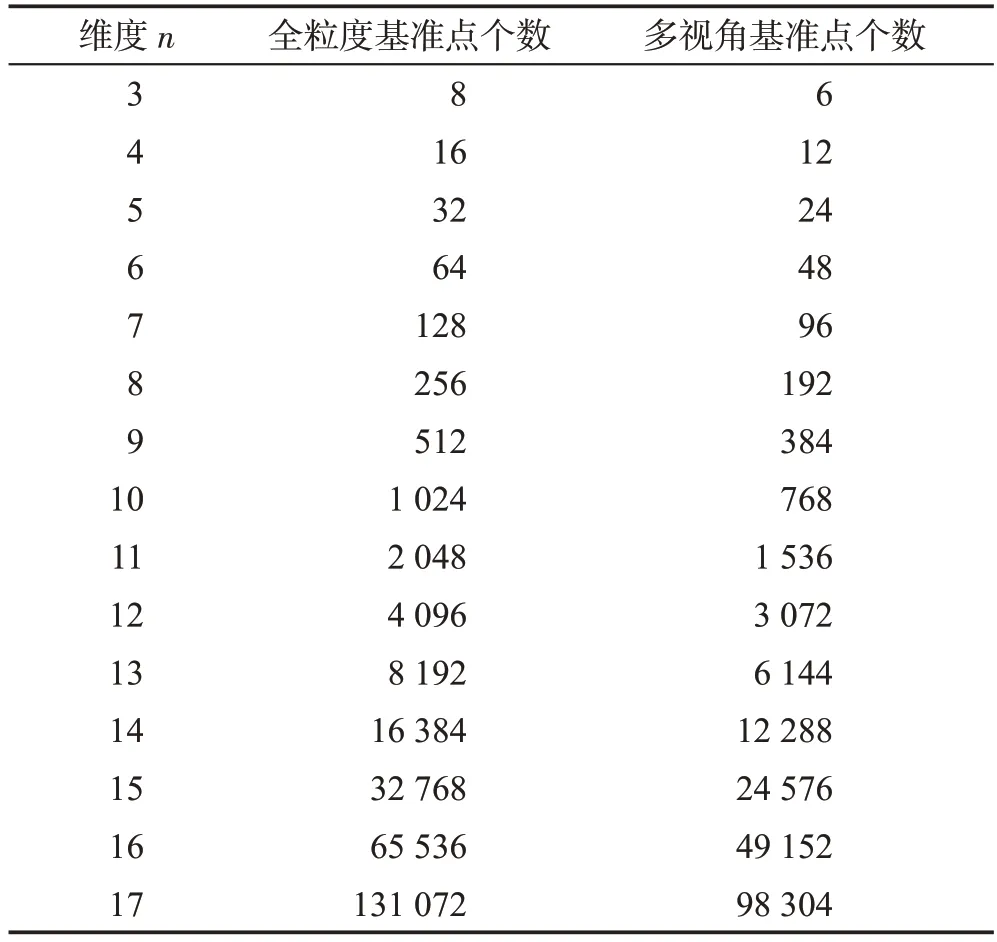
表3 全粒度和多视角方法基准点集规模比较Table 3 Comparison of datum set size between full granularity and multi-perspective methods

基准点集合Sh包含各个角度的数据对象，因此多视角下余弦距离能够更合理地衡量两个高维数据对象之间的相似度。本文将多视角余弦距离作为层次聚类的距离度量方式，应用到无线网络入侵检测算法中，得到了更加准确的检测结果。但是，相较传统欧式距离采用余弦距离度量方式计算高维数据对象之间距离，聚类算法的时间复杂度也明显提高，保证了较高检测率、较低误检率的同时在一定程度上影响了入侵检测算法的检测效率。因此，本文在预处理无线网络数据集时采用主成分分析法对数据集进行降维处理，减小聚类算法时间复杂度对入侵检测算法检测效率的影响。

1.4 主成分分析法对无线网络数据降维

在无线网络数据分析问题的研究中，每一条网络数据往往会涉及数十个甚至上百个属性变量。属性变量太多不但会增加检测算法的时间复杂度，同时也会给合理分析检测结果带来困难[13]。一般来说，虽然网络数据的每个属性变量都提供了一定的信息，但其重要程度也就是贡献度有所不同。而且，在多数情况下，网络数据的各个属性变量之间会存在一定的相关性，从而使得这些属性变量所提供的信息在一定程度上有所重叠，并影响检测结果的准确度。因此，本文采取主成分分析法对这些属性变量加以处理，用为数较少的变量代替原有的属性变量，从而实现对无线网络数据的降维。降维过程如下：

在无线网络数据集AWID（154个属性）[14]中提取对于聚类结果有影响的77维属性进行主成分分析法降维处理，得到的主成分方差贡献率、主成分累计方差贡献率如表4 所示。在用主成分分析法对无线网络数据集进行降维时，可通过调整主成分累计方差贡献率阈值R，选定合适数量的主成分。主成分数量的选择直接影响对原有网络数据的刻画能力。选择为数较少的主成分代替原有数据可能会出现聚类结果不佳、入侵检测算法检测性能大大下降的问题。选择为数较多的主成分代替原有数据又无法实现降维的目的。因此，如何选择合适数量的主成分来代替原有网络数据需要根据具体算法和算法功能来决定，以达到在保证算法较高性能的基础上最大限度实现数据降维的目的。经多次实验，本文选取降维后的前16 个属性进行入侵检测实验，得到了最为理想的检测结果。当再增加属性进行实验时，时间复杂度逐步上升，但是入侵检测结果并无明显改变，y因此本文选用前16个属性。

表4 主成分分析法降维数据结果Table 4 Dimension reduction data results of principal component analysis 单位：%

2 多视角层次聚类的无线网络入侵检测算法

输入：包含n个数据对象的样本集X={x1,x2,…,xn}，多视角步长N，层次聚类阈值a，权值向量l=(l1,l2,…,lp)T。

输出：聚类结果集C。

（1）通过权值向量l=(l1,l2,…,lp)T 降维数据集X={x1,x2,…,xn}中的所有数据对象。

（2）将数据集X={x1,x2,…,xn}中每一个数据对象看作一个初始聚类簇，即构建初始聚类簇U={U1,U2,…,Un}，其中U1={x1},U2={x2}，…，Un={xn}。

（3）遍历所有初始聚类簇中的数据对象xi，计算dist(xi,xj)(xi∈Ui,xj∈Uj,i≠j) 。当∃Mindist(xi,xj)(xi∈Ui,xj∈Uj,i≠j)＜a时，更新聚类簇集为U={U1,U2,…,Un-1}，其中，U1={x1}，U2={x2}，Ui={xi,xj}，…，Un-1={xn}。否则，算法结束，重新输入合理的层次聚类距离阈值a。

（4）由多视角步长N确定基准点集Sh={d1,d2,…,dh}。

（5）遍历聚类簇U={U1,U2,…,Un-1}中所有簇，当∃Mind(Ui,Uj) ＜a时，合并簇Ui、Uj。更新聚类簇U={U1,U2,…,Un-2},其中，

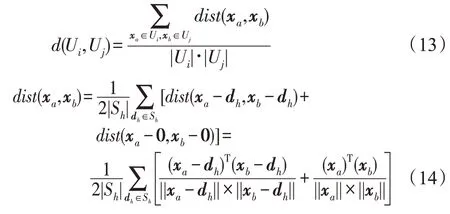
否则，输出聚类结果集U。

（6）重复执行步骤（5），输出最终聚类结果集U。

3 实验与结果分析

实验环境为Windows 10操作系统、Intel i5 CPU、8 GB 内存，实验数据为无线网络数据集AWID，在python3.7进行了如下对比实验：

（1）基于传统K-means 聚类、KNN 分类、密度聚类（density-based spatial clustering of applications with noise，DBSCAN）的入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法对比实验。

（2）基于传统欧式距离层次聚类的无线网络入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法对比实验。

（3）基于全粒度余弦距离层次聚类和多视角余弦距离层次聚类的网络入侵检测算法对比实验。

（4）采用基于传统K-means 聚类、KNN 分类、密度聚类DBSCAN的入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法进行检测未知攻击类型的对比实验。

3.1 实验数据集

AWID 数据集来源于Kolias，是数据量最大也是最全面的真实WiFi网络环境下采集的网络攻击数据集。按照攻击类型级别，数据集被划分为两种数据子集：4种大攻击类型的CLS数据集和16种子攻击类型的ATK数据集。后者的16种子攻击类型包含在前者的4种大攻击类型当中，如ATK数据集中的Caffe-Latte、Hirte、Honeypot 和EvilTwin 攻击类型属于CLS数据集中的伪装攻击类型。同时AWID 数据集包含完整数据集和精简数据集两个版本。本文使用精简版本的CLS 数据集，数据集中数据类型分布情况如表5所示，数据集中的一条normal数据记录为：

表5 数据分布情况Table 5 Data distribution

数据集预处理的过程包括数据完整化、数据合理化、字符型数据数值化、数据标准化、数据属性降维。

（1）数据裁剪

AWID数据集中，少数网络数据的部分属性处于缺失状态，为了保证算法结果的有效性，将属性缺失率达到80%及以上的属性予以删除，其余处于缺失状态的属性位均以0进行填充。

（2）数据选择

本文无线网络数据集中正常行为记录数量远大于攻击行为记录数量，现实网络环境中正常行为记录和攻击行为记录比例确是如此。但是在构建分类器也就是聚类过程中，不同数据类型数据量的比例失衡会直接导致聚类簇大小差异过大，影响了入侵检测模型的效果。为此，本文选取1∶1的正常行为记录和攻击行为记录作为训练数据集构建分类器。为了充分验证文中算法对不同攻击类型数据行为的检测性能，本文同样选取1∶1的正常行为记录和攻击行为记录作为测试数据集，尽可能包含较多攻击类型的攻击行为并且保证同一攻击类型数据行为的数据量也较多。

（3）字符型数据数值化

将无线网络数据集AWID 中的十六进制属性值转化为十进制属性值，将数据集中MAC地址属性转化为其在整个数据集中出现的次数，将字符形式的数据属性值采用one-hot 编码[15]方式进行数值化处理，经由编码方式处理后的字符型属性变量能够更合理地保留原有属性对聚类结果的影响度。

（4）数据属性降维

AWID 数据集中的无线网络数据具有154 个属性值，本文实验前先将测试数据集中所有数据取值均相同的属性删除，并运用主成分分析法提取出贡献率较大的属性，实现对无线网络数据的降维处理，一定程度上降低层次聚类算法的时间复杂度。

（5）数据标准化

数据集中不同属性的值域不同，为了降低这种差别给检测模型带来的影响，需要对数据集中的数据进行z-score 标准化[16]，使其符合正态分布。经验证，在分类和聚类算法中，若需要使用距离来度量相似性并使用PCA 技术进行降维时，z-score 标准化要优于Min-max normalization。

式中，yi表示xi标准化之后的数据，xi表示第i个特征值，μ表示该特征的数据均值，σ表示该特征的数据标准差。

3.2 实验结果与分析

本文采用检测率ACC、误检率FAR、召回率Recall、F1 作为本文无线网络入侵检测算法的性能评价指标。具体如下：

（1）检测率ACC，被正确判定类别的网络数据和网络数据总和的比值。检测率越高，入侵检测算法的性能越好。

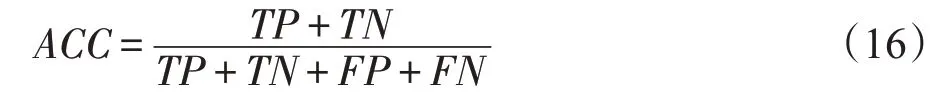
（2）误检率FAR，被错误判定为攻击行为的正常行为数据量和正常行为数据总和的比值。在入侵检测算法中，误检率越低，算法的检测性能越好。

（3）召回率Recall，被正确识别为网络攻击行为的数据量和攻击行为总量的比值。召回率越高，代表入侵检测算法检测攻击行为的能力越强。

（4）F1，综合考虑算法各项性能的指标。F1 的值越大，代表入侵检测算法的整体性能越好。

其中，TN（true negative）表示把正常网络数据行为正确识别为normal 的网络数据行为数量；TP（true positive）表示把网络攻击行为正确判别为相应攻击类型的网络数据数量；FN（false negative）表示把网络攻击行为错误识别为正常网络数据行为的数据数量；FP（false positive）表示把正常数据行为错误判别为某种攻击行为的网络数据数量。

表6和表7所示的H1～H10 和D1～D10 为本文实验所使用的数据集，均为CLS 数据集的抽样数据集。为避免入侵检测算法在单一实验数据集上测试带来的实验结果偶然性，本文在CLS 数据集中随机抽取带有不同攻击行为类的大小不一的实验数据集H1～H10、D1～D10 进行实验。其中，数据集D1～D10的攻击行为数据中均包含相应类别数的若干条未知攻击行为数据（由已知攻击行为伪装而成），用于入侵检测算法检测未知攻击行为性能的对比实验。

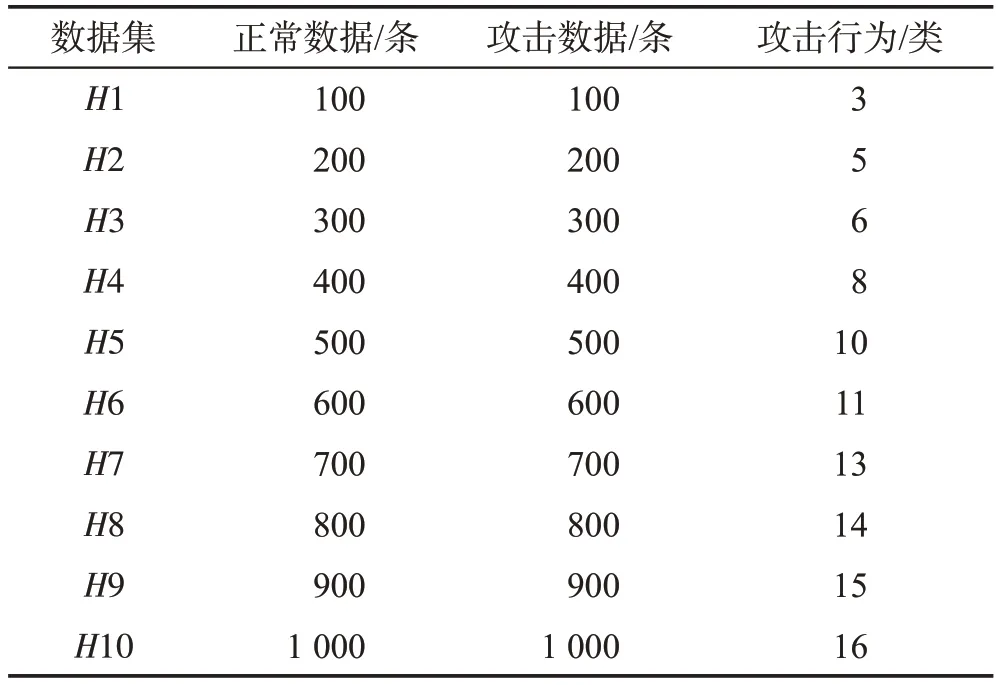
表6 实验1、实验2和实验3的测试数据集Table 6 Test dataset of experiment 1,2 and 3

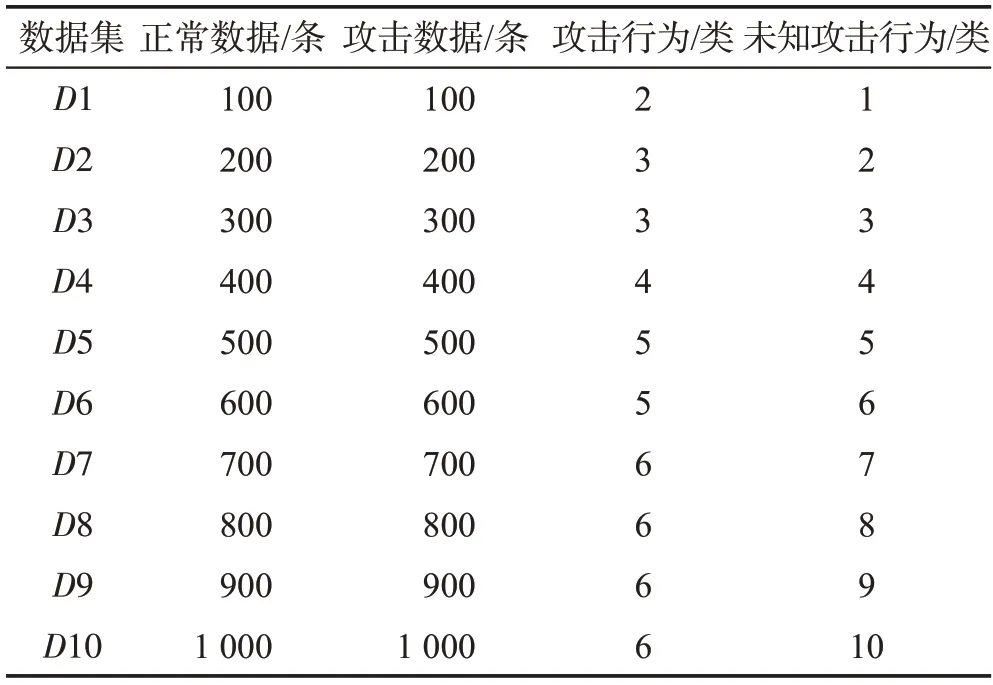
表7 实验4的测试数据集Table 7 Test dataset of experiment 4

3.2.1 对比实验1

采用基于传统K-means 聚类、KNN 分类、密度聚类DBSCAN的入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法进行对比实验。分别选用H1、H2、H3、H4、H5、H6、H7、H8、H9、H10 测试数据集进行10次对比实验。实验结果如图7～图10所示。

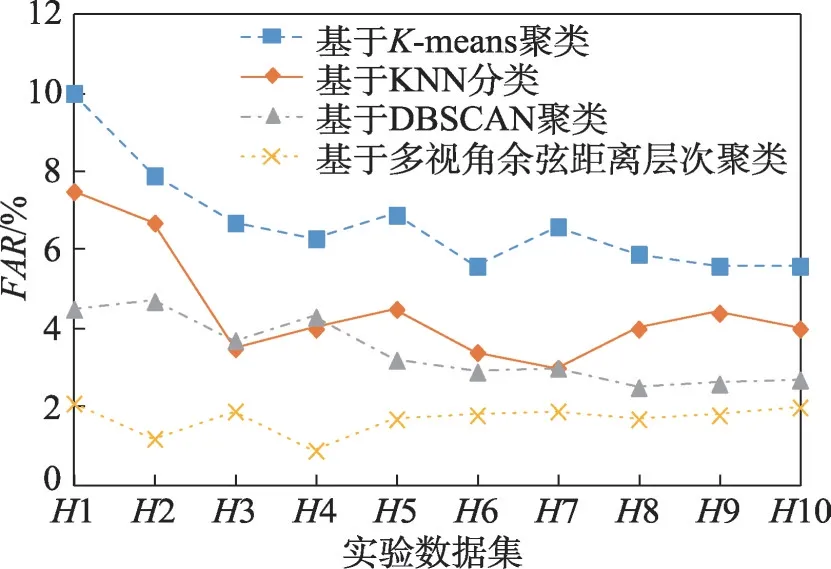
图8 实验1 FAR 对比Fig.8 Comparison of FAR in experiment 1

图9 实验1 Recall 对比Fig.9 Comparison of Recall in experiment 1

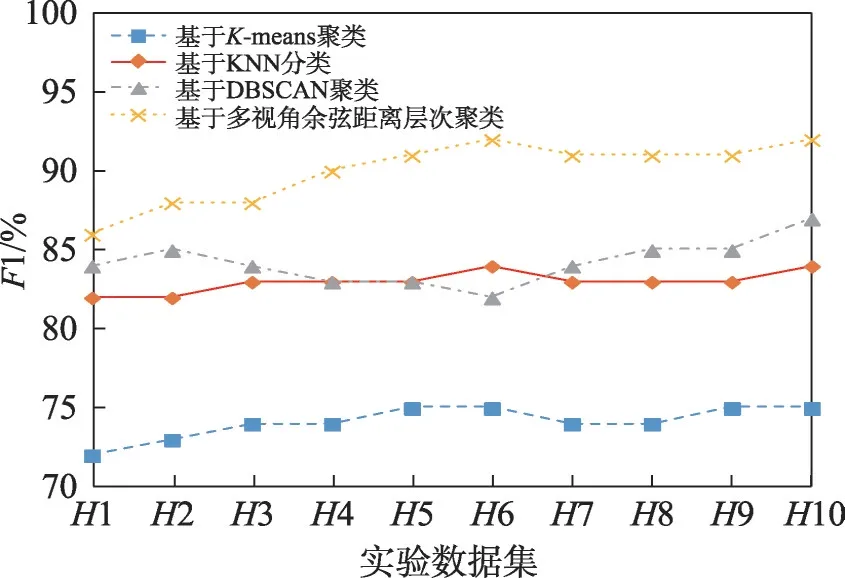
图10 实验1 F1 对比Fig.10 Comparison of F1 in experiment 1

3.2.2 对比实验2

采用基于传统欧式距离层次聚类的无线网络入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法进行对比实验。分别选用H1、H2、H3、H4、H5、H6、H7、H8、H9、H10 测试数据集进行10 次对比实验。实验结果如图11～图14所示。

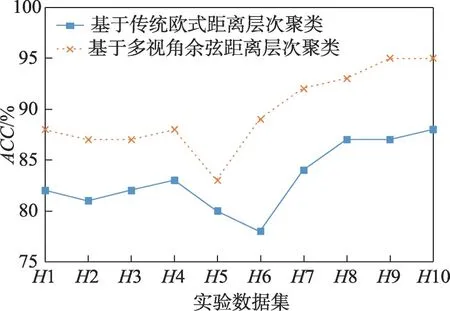
图11 实验2 ACC 对比Fig.11 Comparison of ACC in experiment 2

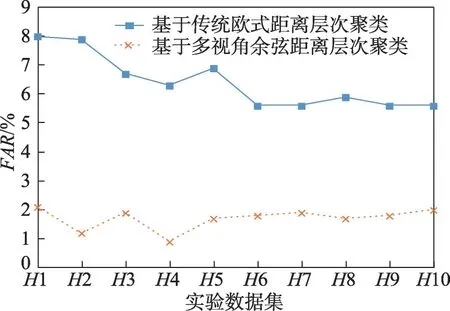
图12 实验2 FAR 对比Fig.12 Comparison of FAR in experiment 2

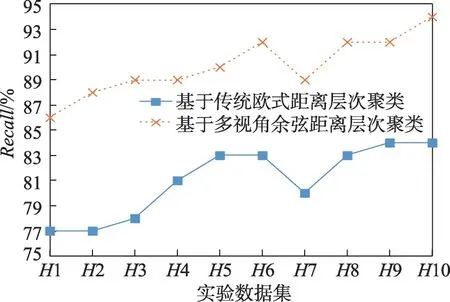
图13 实验2 Recall 对比Fig.13 Comparison of Recall in experiment 2

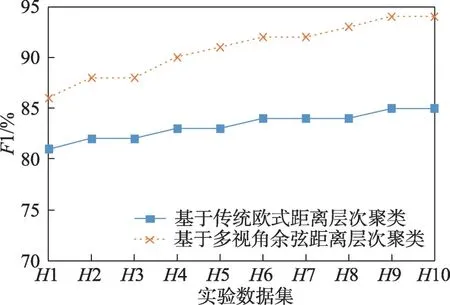
图14 实验2 F1 对比Fig.14 Comparison of F1 in experiment 2

3.2.3 对比实验3

基于全粒度余弦距离层次聚类和基于多视角余弦距离层次聚类的网络入侵检测算法进行对比实验。分别选用H1、H2、H3、H4、H5、H6、H7、H8、H9、H10 测试数据集进行10次对比实验。实验结果如图15～图18所示。

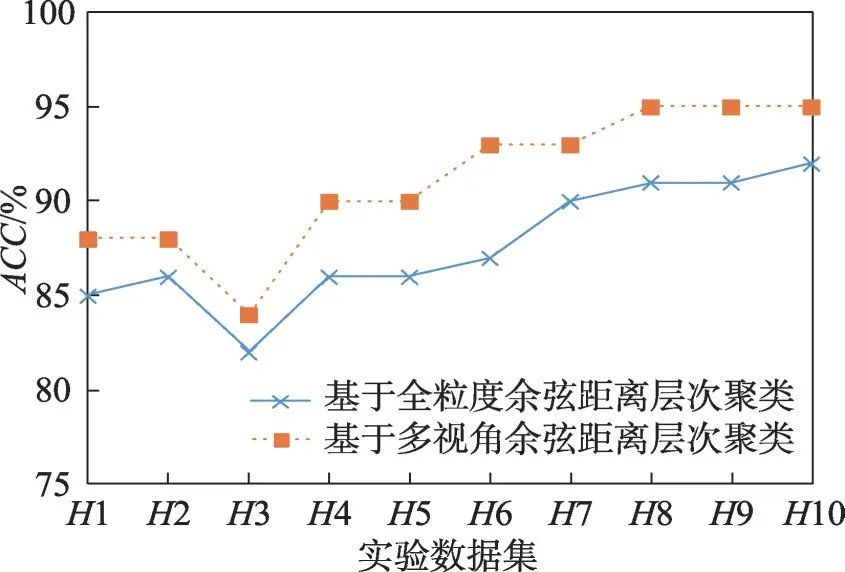
图15 实验3 ACC 对比Fig.15 Comparison of ACC in experiment 3

图16 实验3 FAR 对比Fig.16 Comparison of FAR in experiment 3

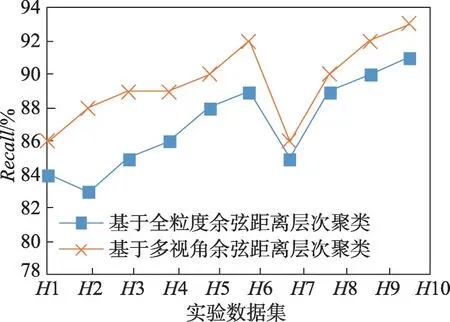
图17 实验3 Recall 对比Fig.17 Comparison of Recall in experiment 3

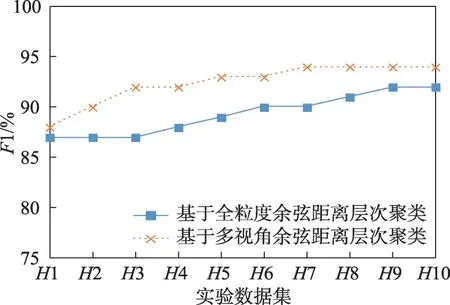
图18 实验3 F1 对比Fig.18 Comparison of F1 in experiment 3

3.2.4 对比实验4

采用基于传统K-means 聚类、KNN 分类、密度聚类DBSCAN的入侵检测算法和基于多视角余弦距离层次聚类的无线网络入侵检测算法进行检测未知攻击类型的对比实验。分别选用D1、D2、D3、D4、D5、D6、D7、D8、D9、D10 测试数据集进行10 次对比实验。实验结果如图19所示。

图19 实验4未知攻击类型检测率Fig.19 Detection rate of unknown attack type in experiment 4

通过上述四种对比实验，结果表明，相较基于传统K-means 聚类、KNN 分类以及密度聚类DBSCAN的入侵检测算法，本文提出的基于多视角层次聚类的无线网络入侵检测算法在入侵检测算法四项性能指标ACC、FAR、Recall、F1 上均有明显改善，并且在发现未知攻击类型方面也有了很大提升。相较基于传统欧式距离层次聚类的入侵检测算法，基于多视角余弦距离层次聚类的无线网络入侵检测算法具有更高的ACC、Recall和F1 以及较低的FAR。通过主成分分析法降维后的无线网络攻击数据集AWID 能够很好地代表原有属性的特征，在实现了数据集降维、降低算法时间复杂度、提高算法检测效率的同时保证了较高的ACC、Recall、F1 以及较低的FAR。

4 结束语

为提升基于聚类的无监督无线网络入侵检测算法性能，本文构建了在多视角层次聚类下的无线网络入侵检测算法，该算法引入多视角余弦距离作为层次聚类过程中数据对象间相似性度量方式，使得无线网络数据的聚类结果更加合理，在一定程度上提高了入侵检测算法的检测率，降低了误检率。提出的多视角选取基准点的方法虽较全粒度选取基准点方法在基准点集规模上有了明显改善，不过随着数据维度的增高，基准点集规模依然会很大，影响入侵检测算法的整体性能。下一步工作，将寻找更加合理有效的基准点选取方式和实验数据降维方式，进一步降低聚类算法的时间复杂度和提高入侵检测算法的整体性能。