基于直观图的三支概念获取及属性特征分析
万 青,马盈仓,李金海
1.西安工程大学 理学院,西安 710048
2.西北大学 概念、认知与智能研究中心,西安 710127
3.昆明理工大学 理学院,昆明 650500
4.昆明理工大学 数据科学研究中心,昆明 650500
形式概念分析理论[1]是Wille 于1982 年提出的,用于概念的发现、排序和显示,是知识发现的有效数学理论。该理论的基础数据是形式背景,Wille 通过概念诱导算子提取了形式背景中“共同具有”的共性信息,进而形成概念格。随后,借鉴粗糙集理论[2]中的上、下近似思想,Gediga和Duntsch以及Yao[3-4]提出了面向对象概念格和面向属性概念格,将形式背景中部分具有的信息提炼出来。此外,2014年,Qi等将三支决策理论[5]的思想引入形式概念分析,提出了对象诱导的三支概念格和属性诱导的三支概念格这两种模型,它们既可以表达形式背景中“共同(被)具有”的共性信息,也可以表达“共同不(被)具有”的共性信息,使得获取的知识更为丰富,为知识发现提供了新的理论——三支概念分析[6]。
目前,关于该理论的研究包括三支概念格的构建、模型推广、属性约简、规则获取、与其他理论的结合以及应用等方面。比如,在三支概念格构造与模型推广方面,Qi等[7]较为深入地分析了概念格与三支概念格之间的关系,基于此Qian 等通过形式背景的并置与叠置研究了三支概念格的构造方法[8],并提出了对象诱导的三支面向对象概念格和属性诱导的三支面向属性概念格的定义,详细分析了这四种三支概念格之间的关系[9-10]。Yu等[11]讨论了三支概念格的一些特殊性质,并建立了某些特殊完备格和三支概念格之间的同构映射。Yao[12]讨论了不完备背景上的三支概念。Li 等[13]基于粗糙集上、下近似的思想,在不完备背景上提出了三支近似概念。
在属性约简方面,Ren等[14]研究了三支概念格的四种约简,并分析了不同类型的约简之间的关系。李美争等[15]构造了一种对象-概念辨识矩阵,基于此研究了三支近似概念格的约简。在规则获取方面,Wei等[16]基于三支概念格,在三支协调的意义下研究了决策背景的规则获取问题,并与强协调决策背景所获得的一般决策规则进行了详细的比较研究。此外,任睿思等[17]讨论了弱协调意义下的三支规则获取问题。
在三支概念分析理论与其他理论结合方面,Li等[18-19]提出了基于多粒度的三支认知概念学习。徐伟华等[20]讨论了模糊三支概念的概念认知学习方法。龙柄翰等[21]提出了模糊三支概念分析,考虑模糊背景中“共同具有的程度”与“共同不具有的程度”两方面不确定的共性信息。基于此,姬儒雅等[22]提出了毕达哥拉斯模糊三支概念格,而Singh[23]利用中智集提出了一种新的三支模糊概念格的模型。此外,三支概念格现已被应用于医疗诊断[24]、认知记忆[25]以及文本分类[26]等领域。
由于在形式概念分析中,可以通过形式背景的直观图获取形式概念、面向对象概念和面向属性概念,也可以用于判别属性特征[27-28],而四种三支概念又可以通过特殊的形式背景(形式背景与其补背景的叠置和并置)的形式概念进行一定的转化而得到[8-10]。因此,很自然的一个想法就是,通过这类特殊形式背景的直观图研究四种三支概念的获取方法及相应的三支概念格的约简。
于是,本文的主要目的就是结合三支思想提出形式背景的另外两种新的直观图,并基于此研究三支概念的获取方法以及三支概念格的属性特征分析。首先,从属性集出发,给出形式背景的属性混合直观图和属性对诱导的三支直观图的定义,以此为基础研究对象诱导的三支概念和对象诱导的三支面向对象概念的获取方法;其次,对偶地,从对象集出发,提出对象混合直观图和对象对诱导的三支直观图的定义,给出属性诱导的三支概念和属性诱导的三支面向属性概念的获取方法;最后,对于格约简和属性特征分类给出一般化的定义,并针对对象诱导的三支概念格,基于差别矩阵对其属性特征进行分析,给出相应的判别定理,进而通过属性对诱导的三支直观图得到属性特征的判别方法。
1 预备知识
本章主要介绍直观图和三支概念分析的相关概念。
1.1 形式背景及直观图的基础知识
定义1[1]称(G,M,I)为一个形式背景,其中G={x1,x2,…,xp}为对象集,每个xi(i≤p)称为一个对象;M={a1,a2,…,aq}为属性集,每个aj(j≤q)称为一个属性;I为G和M之间的二元关系,I⊆G×M。若(x,a)∈I,则表示对象x具有属性a,记为xIa。
注1本文所研究的形式背景是有限的且是正则的。
对于形式背景K=(G,M,I),Wille 在对象子集X⊆G和属性子集A⊆M上定义两个导出算子,具体定义如下:

特别地,对任意的x∈G,a∈M,记{x}*为x*,{a}*为a*。
若满足X*=A且A*=X,则称(X,A)是一个形式概念,简称概念;其中,称X为概念的外延,A为其内涵。用L(K)表示所有概念的集合,记
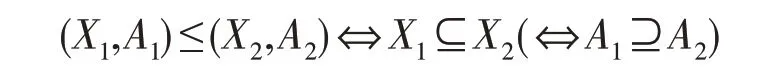
则“≤”是L(K)上的偏序关系。对于任意两个概念,定义下确界和上确界,如下:
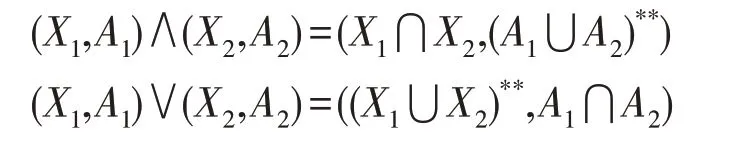
从而(L(K),≤)形成了完备格,称为概念格,并简记为L(K)。记所有概念的外延的集合和内涵的集合分别为LG(K)和LM(K)。
对于L(K)中的任意两个概念(X1,A1),(X2,A2),若(X1,A1)≤(X2,A2),且不存在(X,A)∈L(K),有(X,A)≠(X1,A1),(X,A)≠(X2,A2),使得(X1,A1)≤(X,A)≤(X2,A2),则称(X2,A2)是(X1,A1)的父概念,(X1,A1)是(X2,A2)的子概念,并记为(X1,A1)≺(X2,A2)。
另外,对任意的X⊆G和A⊆M,一对近似算子□和 ⋄定义如下:

类似于概念和概念格的形成过程,Gediga 和Duntsch以及Yao分别提出了面向属性概念格LP(K)和面向对象概念格LO(K),更多的关于这两类概念格的详细内容及相关性质可参考文献[3-4],此处不再赘述。
下面给出形式背景K=(G,M,I)对象/属性直观图的定义。


注2在形式背景中,用[x]表示对象x的等价类,[a]表示属性a的等价类。在文献[27]中,因为所研究形式背景是净化背景,故对象/属性等价类均为单点集,因此将[x]简记为x,[a]简记为a。

例1[14]表1 为形式背景K=(G,M,I),它的对象直观图和属性直观图分别如图1和图2所示。
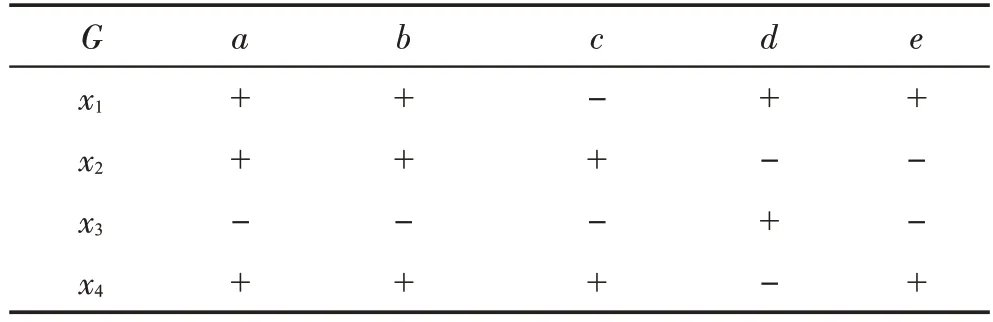
表1 形式背景K=(G,M,I)Table 1 Formal context K=(G,M,I)

图1 对象直观图Fig.1 Object pictorial diagram
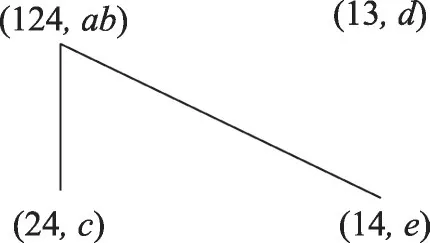
图2 属性直观图Fig.2 Property pictorial diagram
表2为形式背景K=(G,M,I)的补背景。
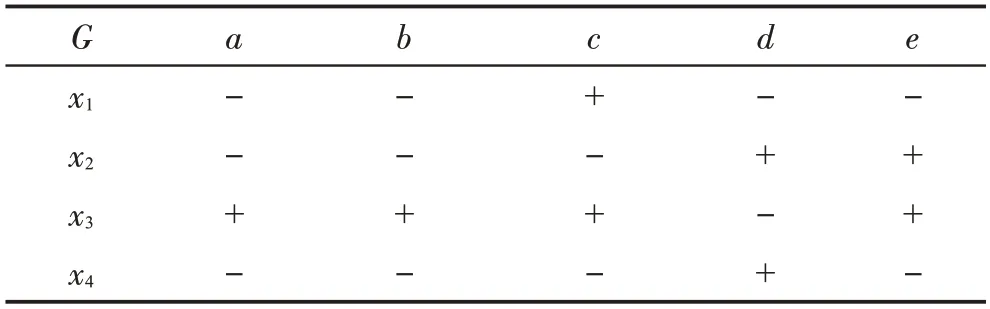
表2 表1的补背景Table 2 Complementary context of table 1
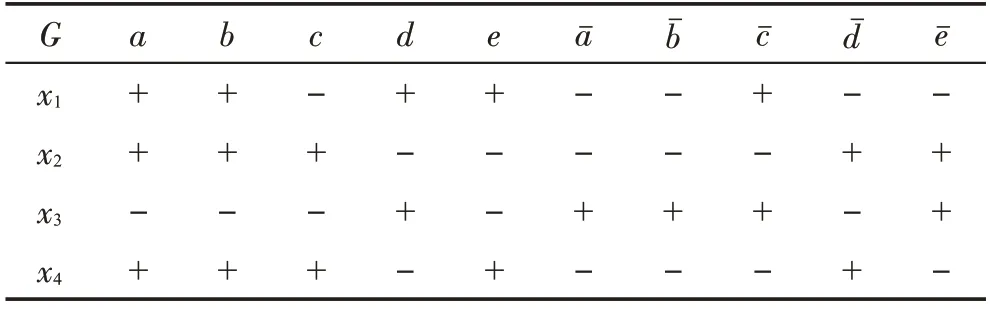
表3 I型混合背景Table 3 Type I-combinatorial context

表4 II型混合背景Table 4 Type II-combinatorial context
1.2 三支概念格的基础知识
本节首先对任意非空有限集合幂集的笛卡尔积上的运算进行回顾。
令S是一个非空有限集,P(S)是其幂集,DP(S)=P(S)×P(S)。则DP(S)是布尔代数,其上的交、并、补等运算可以通过标准的集合运算来定义。也就是说,任意的(A,B),(C,D)∈DP(S),那么:

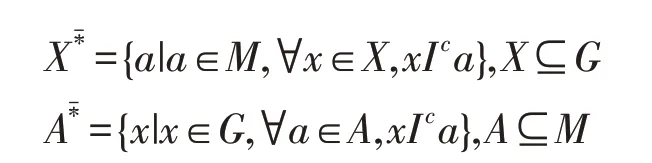
事实上,形式背景中的负算子ˉ*是其补背景上的概念导出算子*。
2016 年Qi 等通过结合正算子和负算子,在形式背景中提出了两种三支算子:OE 算子和AE 算子。下面给出这两个算子的相关知识的介绍。

当X⋖=(A,B)且(A,B)⋗=X时,称(X,(A,B))为对象诱导的三支概念,简称为OE 概念。其中,称X为OE 概念的外延,(A,B) 为其内涵。用OEL(K) 表示K=(G,M,I)中所有OE概念的集合,并记所有OE概念的外延的集合和内涵的集合分别为OELG(K) 和OELM(K)。
当 (X,Y)⋗=A且A⋖=(X,Y)时,称((X,Y),A)为属性诱导的三支概念,简称为AE概念。其中,称(X,Y)为AE 概念的外延,A为其内涵。用AEL(K)表示所有AE 概念的集合,记所有AE 概念的外延的集合和内涵的集合分别为AELG(K)和AELM(K)。
对于OEL(K)和AEL(K),类似于概念格的形成过程,通过定义偏序关系“≤”以及上确界“∨”、下确界“∧”运算,可得(OEL(K),≤)和(AEL(K),≤)也形成了完备格,分别称为对象诱导的三支概念格和属性诱导的三支概念格,并依次简记为OEL(K)和AEL(K)。
类似于形式背景中负算子ˉ*的定义,对任意X⊆G和A⊆M,定义□和⋄的负算子分别为:

基于此,Qian等提出了另外两种三支算子:OEO算子和AEP算子。


类似于面向对象概念格和面向属性概念格,Qian等进而提出了对象诱导的三支面向对象概念格OEOL(K)和属性诱导的三支面向属性概念格AEPL(K)。记所有对象诱导的三支面向对象(属性)概念的外延的集合和内涵的集合分别为OEOLG(K)和OEOLM(K)(AEPLG(K)和AEPLM(K))。关于这两种三支概念格的更多详细的内容可参考文献[9]。
对于对象诱导的三支概念格OEL(K)、属性诱导的三支概念格AEL(K)、对象诱导的三支面向对象概念格OEOL(K)和属性诱导的三支面向属性概念格AEPL(K),这四种三支概念格中父子概念的定义与经典概念格中的完全一致。另外,这四种三支概念格与I 型和II 型混合背景的三种概念格之间具有如下的关系。
引理1[10]设K=(G,M,I)是形式背景,分别是该形式背景的I 型混合背景和II 型混合背景。则有:

引理1 揭示了形式背景的这四种三支概念格与经典概念格、面向对象(属性)概念格之间的内在关联性,进一步由引理1可以得到如下结论。
推论1设K=(G,M,I)是形式背景。对任意x∈G和a∈M,则有下列结论成立。

类似地,也可证得(2)、(3)和(4)是成立的。
例2(续例1)对于表1的形式背景,它的四种三支概念格分别如图3~图6所示。

图3 表1的OEL(K)Fig.3 OEL(K)of table 1

图4 表1的AEL(K)Fig.4 AEL(K)of table1
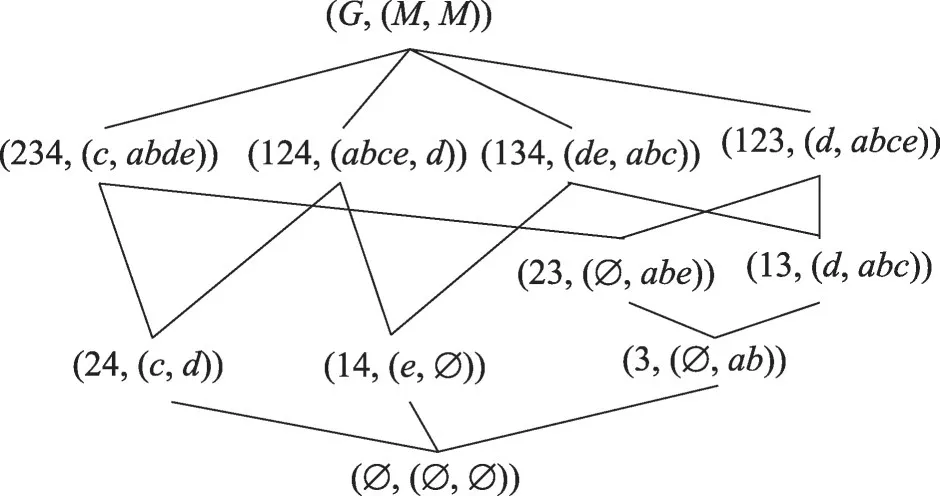
图5 表1的OEOL(K)Fig.5 OEOL(K)of table 1

图6 表1的AEPL(K)Fig.6 AEPL(K)of table 1
2 OE概念和OEO概念的获取方法
在形式背景中,经典概念和面向对象概念均可通过形式背景的属性直观图来获取,具体的方法如下。
引理2[27]设K=(G,M,I)是形式背景,(HM,≤)是该形式背景的属性直观图。则有:
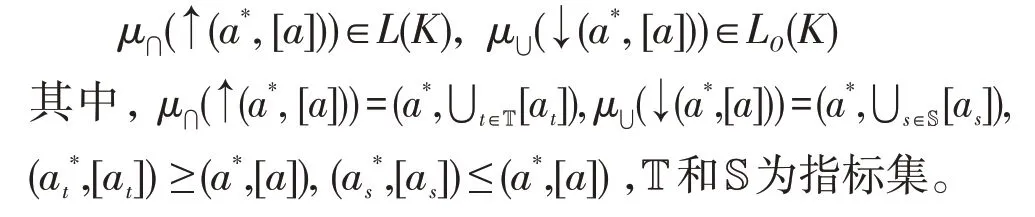
在引理2的基础上,再通过概念的交、并运算,便可以获得L(K)和LO(K)。
受引理2 的启发,本文借助引理1 的结论,通过给定形式背景的I 型混合背景的属性直观图研究对象诱导的三支概念和对象诱导的三支面向对象概念的获取方法。首先,给出如下的定义。
定义5设K=(G,M,I)是形式背景,是K的I型混合背景。记:

通过引理2可从(HM∪Mˉ,≤)获取中的经典概念和面向对象概念。于是,结合引理1,可从属性混合直观图(HM∪Mˉ,≤)直接获取K=(G,M,I)中的OE 概念和OEO概念的方法。


且可验证这些OE概念都是(G,(∅,∅))的子概念。
例3(续例1)表1 所示形式背景的属性混合直观图如图7所示。

图7 属性混合直观图Fig.7 Combinatorial-property pictorial diagram

对图7的属性混合直观图(HM∪Mˉ,≤)进行属性分离映射[·]m,所得属性对诱导的三支直观图如图8所示。

图8 属性对诱导的三支直观图Fig.8 Property pair induced three-way pictorial diagram

而(24,(c,d))∈OEOL(K),此结果可由图5验证。
3 AE概念和AEP概念的获取方法
利用形式背景中对象集与属性集的对偶性,从对象集的角度提出了对象直观图,由它可以获取形式背景的经典概念和面向属性概念。进一步,再通过概念的交、并运算,便可以获得L(K)和LP(K)。
引理3[27]设K=(G,M,I)是形式背景,(HG,≤)是该形式背景的对象直观图。则有:



且可验证这些AE概念都是((∅,∅),M)的父概念。
例4(续例1)表1所示形式背景的对象混合直观图和对象对诱导的三支直观图如图9和图10所示。
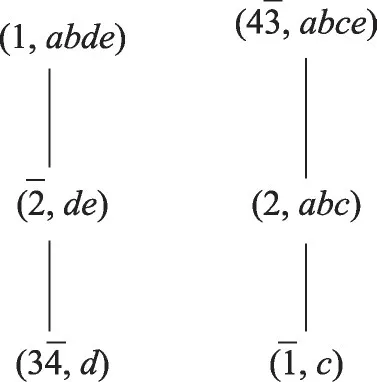
图9 对象混合直观图Fig.9 Combinatorial-object pictorial diagram

图10 对象对诱导的三支直观图Fig.10 Object pair induced three-way pictorial diagram


该结果可由图6验证((3,24),de)∈AELP(K)。
4 三支概念格的属性特征分析
本章只讨论形式背景的不同类型的概念格保持其格结构不变的约简,简称为约简。
对于形式背景K=(G,M,I),它的任意的一类概念格记为α(G,M,I),相应的外延集合记为αG(G,M,I)。下面给出约简的一般化定义。
定义9设K=(G,M,I)是形式背景,α(G,M,I)是其某一类概念格。若存在属性子集D⊆M,使得αG(G,D,ID)=αG(G,M,I)成立,则称D是α(G,M,I)的协调集;如果对于任意的d∈D,都有αG(G,D-{d},ID-{d})≠αG(G,M,I),则称D是α(G,M,I)的约简。
本文仅限定α的取值为{K,OE,AE,OEO,AEP},依次代表经典概念格L(K)、对象诱导的三支概念格OEL(K)、属性诱导的三支概念格AEL(K)、对象诱导的三支面向对象概念格OEOL(K)以及属性诱导的三支面向属性概念格AEPL(K)。
属性特征分类的一般化定义如下。

这三类属性在构造约简的过程中起着不同的作用。其中,每一个核心必包含于每一个约简之中,是必不可少的;每一个绝对不必要属性是必不包含在任意一约简之中,是完全可以删除的;每一个相对必要属性是包含于部分约简之中,类型比较特殊。
对于形式背景K=(G,M,I)的四种三支概念格,由引理1可知,AEPL(K)与AEL(K)的约简相同,OEOL(K)与OEL(K)的约简相同。而且,AEL(K)没有绝对不必要属性,若存在a*=b*(a,b∈M),则表明属性a和b是一类相对必要属性[14]。因此下面只需讨论OEL(K)的约简。
差别矩阵是寻找约简最常见的计算方法,OEL(K)的差别矩阵定义如下。
定义11[14]设K=(G,M,I)是形式背景,(X,(A,B)),(Y,(C,D))∈OEL(K),则称:

是对象导出三支概念(X,(A,B))与(Y,(C,D))的差别属性集。其中,(X,(A,B))≺(Y,(C,D))表示(X,(A,B))是(Y,(C,D))的子概念。
在此基础上,称集合:
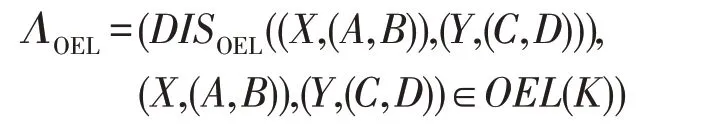
为OEL(K)的差别矩阵。
注3因为只有差别矩阵中的非空元素对约简有意义,所以把非空元素的集合也记为ΛOEL,两者不加区别。此外,在具体计算时,差别集用集合的并表示,即用(A-C)∪(B-D)代替(A-C,B-D)。
因LG(K|)=OELG(K),所以这两种格的差别矩阵ΛOEL和ΛL(K|Kˉ)之间必存在如下的一一对应关系。
推论2设K=(G,M,I)是形式背景,[·]m为属性分离映射。对任意的H∈ΛL(K|Kˉ),[H]m=(H1,H2),则有H1∪H2∈ΛOEL且|ΛL(K|Kˉ)|=|ΛOEL|。
在经典概念格的约简中,差别矩阵元素若为单点集,则其唯一的元素必为核心。这个性质对于OEL(K)来说仍然成立,且可通过推论2得到。
定理5设K=(G,M,I) 是形式背景。对任意的a∈M,a∈COE⇔∃(X,(A,B)),(Y,(C,D))∈OEL(K),使 得DISOEL((X,(A,B)),(Y,(C,D)))={a}。
由此,可以通过OEL(K)的差别矩阵得到核心属性的判别方法。
引理4设K=(G,M,I) 是形式背景,(X,(A,B))∈OEL(K),且(X,(A,B))是(G,(∅,∅))的子概念。则∀a∈A,b∈B,总有a*∩b*ˉ=X。
证明若|A|=1,|B|=0 或|B|=1,|A|=0,则根据OE概念的定义可知该结论显然成立。即当|A∪B|=1时,结论成立。
当|A∪B|≥2 时,分为以下三种情况进行证明。

综合上述分析,可证原命题成立。
通过引理4可以得到下述判断OEL(K)的核心和相对必要属性的方法。
定理6设K=(G,M,I) 是形式背景,(X,(A,B))∈OEL(K),且(X,(A,B))是(G,(∅,∅))的子概念。则以下命题成立:
(1)若|A∪B|=1,则A∪B中元素是核心。
(2)若|A∪B|≥2,则A∪B中元素是相对必要属性。
证明(1)由于|A∪B|=1,DISOEL((X,(A,B)),(G,(∅,∅)))=A∪B是单点集。根据定理5 可知,A∪B中元素是核心。
(2)若|A∪B|≥2,则由定理5 可知A∪B中元素一定不是核心。以下分三种情况进行说明。
①对于|A|≥2,|B|=0 的情况,根据引理4 可知,∀a∈A,都有a*=X。因此,A中属性属于同一等价类;且A中属性要么同时属于、要么同时不属于某个概念内涵的第一部分。又因M-A不是协调集,于是A中属性属于某个约简。因此A中属性是相对必要属性且属于同一类相对必要属性。
②对于|A|=0,|B|≥2 的情况,与|A|≥2,|B|=0 的证明类似,可得B中属性是相对必要属性且属于同一类相对必要属性。
③对于|A|≥1,|B|≥1的情况,设A={a,c},B={b,d},则由引理4 的证明过程(3)的方法可以证得a*∩c*=b*ˉ∩d*ˉ=X。又进一步由引理4 的证明过程(1)的方法可证a*=c*=b*ˉ=d*ˉ=X。又因M-A∪B肯定不是协调集,所以A∪B中属性是相对必要属性且属于同一类相对必要属性。
由定理6可得相对必要属性具有下述特点。
推论3设K=(G,M,I) 是形式背景。对任意的a∈M,若a∈KOE,则一定存在b∈M,b≠a,满足a*=b*或者a*=b*ˉ。
下面通过属性对诱导的三支直观图将定理6 的结论叙述如下。

从而,根据定理7 可以得到OEL(K)和OEOL(K)的核心属性是e,相对必要属性为a、b、c、d,其中a*=b*,d*=c*ˉ,故a、b属于同一类相对必要属性,c、d属于另一类相对必要属性。故由此可验证定理7的结论。
5 结束语
本文利用形式背景的直观图与概念、面向对象概念和面向属性概念之间的关系,以及四种三支概念与两类混合背景的概念之间的关联性,基于形式背景的混合直观图和三支直观图,提出了获取四种三支概念的方法;通过差别矩阵给出了OEL(K)属性特征的判别方法,并基于此得到了由属性对诱导的三支直观图判别属性特征的方法。后续将进一步借助属性混合直观图研究三支意义下的决策形式背景的协调性的判别方法以及三支规则的获取问题。

