基于MIKE21的跨河桥梁壅水数值模拟分析

孙治平， 赵志宏， 刘子金， 王 鑫， 连海东， 王 燕， 任子豪

(1.中卫市水务局， 宁夏 中卫 755100； 2.华北水利水电大学 水利学院， 河南 郑州 450046；3.浙江省农村水利水电资源配置与调控关键技术重点实验室， 浙江 杭州 310018)

1 研究背景

跨河桥梁对河道的阻水作用明显，导致桥墩附近水位壅高、河道流态发生变化、流速重新分布，从而改变了流速边界条件，易造成河床冲刷、河道淤积、河水漫溢，加大了河道与堤防的防洪负担，大型跨河桥梁的影响尤为显著[1-2]。桥梁对河道水位变化的影响一直以来是研究河道行洪安全所关注的问题[3-6]。在探究河道建筑物对水位和水流流态的影响方面，常采用一维、二维水动力数学模型与河道工程模型试验[7]的方法从定性和定量角度进行研究，如王涛等[8]以吉林省珲春河改造段为研究对象，通过物理模型试验与数值模拟，探讨了北方平原区宽浅河道糙率与桥墩壅水对行洪能力的影响，并用物理模型试验结果验证了一维、二维模型的准确性和合理性；任梅芳等[9]选取海南省南渡江上的6座桥梁为研究对象，构建MIKE21二维水动力模型，计算了不同频率洪水下的桥前壅水值，得到了采用数值模型计算壅水值更加合理的结论；陈文学等[10]利用Flow3D软件模拟南水北调中线工程中桥墩的壅水特性，计算分析了桥墩不同布置形式下的阻水比对壅水值的影响；闫杰超等[11]通过CFD(computational fluid dynamics)流体软件建立3D桥墩水动力模型，对不同工况下墩前壅水及断面平均壅水特性进行了研究，并基于动量守恒原理提出了多桥墩最大壅水高度的预测方法；李润祥等[12]以某斜交跨河桥梁工程为背景，分别采用HEC-RAS(The Hydrologic Engineering Center-river analysis system)模型与二维水动力模型对桥梁壅水计算进行了优化，并选定综合投影方式作为该河道模型最佳概化投影方式；袁晓渊等[13]以淮河入海水道铁路桥为研究对象，运用SMS(surface water modeling system)软件建立二维数值模型，探究了桥墩对行洪水位的影响，并对桥墩形状尺寸进行了优选；朱京德等[14]以连霍高速新城互通新增匝道工程为例，运用二维水动力模型对河道进行了数值模拟，对比分析了匝道桥建设前后河道的流场变化，从多角度分析了工程建设后匝道桥对河道行洪的影响。但在构建数学模型和模拟计算过程中，由于某些河道资料不完善、部分实测数据缺失，往往侧重于对典型影响因素的关注，而缺少对实际工程应用中桥梁壅水的众多影响因素进行全面综合的探究分析，如河道糙率、桥墩形状、尺寸、桥墩个数及流速等，因此模拟结果易产生偏差，针对其结果可靠程度的对比分析还需深入。

鉴于此，本次研究以黄河上游下段河道——宁夏河段青石段内连续7座跨河桥梁为研究对象，综合考虑多项桥梁壅水影响因素，构建二维水动力模型，对不同洪水频率下跨河建筑物造成的河道水流变化情况和各桥梁壅水特性进行数值模拟，并将模拟结果与桥前壅水经验公式的计算结果进行对比分析，可为跨河桥梁壅水影响研究提供参考依据。

2 模型与经验公式简介

2.1 MIKE21简介

MIKE21是由丹麦水力研究所(Denmark Hydraulic Institute)开发的一个专业工程软件包[15]，在平面二维自由表面流数值模拟方面具有强大的功能，用来模拟二维表面自由流，适用于水平尺度远大于垂向尺度条件下垂向流速和垂向加速度可以忽略时，对湖泊、河口、海湾、海岸和海洋的水动力和环境现象的模拟。MIKE21包括水动力、平面扩散、生态过程和泥沙输运4大模块，其中水动力模块为其他模块计算的基础。

本研究主要应用水动力学模块分析河道中桥墩壅水影响，利用水动力学基本原理，基于简单拖曳理论在亚网格结构中计算，模拟水流流速变化对桥墩产生的摩擦力变化。拖曳力F基于流体力学Morrison公式进行计算：

(1)

式中：ρw为水体密度，kg/m3；μ为流线因子，随拖曳力增加而增大；CD为拖曳系数，对于天然河流中直立桥墩取1.2；Ae为迎水面面积，m2；V为断面平均流速，m/s。

2.2 壅水经验公式

国内外研究学者在大量试验和研究的基础上，通过不同理论与方法提出多种桥梁壅水计算经验公式[16-17]。经验公式因其具有形式简单、参数较少、计算简便、便于应用等优点，在工程设计早期被广泛采用，但对于复杂河道与桥梁问题，不同公式在不同对象中的计算偏差较大[18-19]，其计算结果不宜单独应用，但仍可为物理模型试验和数值仿真模拟结果对比分析提供参考。本文采用两种桥前壅水计算经验公式，分述如下。

(1)Henderson公式：

(2)

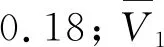
(2)陆浩公式：

(3)

(4)

(5)

K2=1/(1+μ(p-1))

(6)

V1=K2Qs/Aj

(7)

V2=Qs/AG

(8)

式中：KD为定床壅水系数，与水流通过桥下断面时的流速变化有关；K1与桥下水流流态有关；K2为反映流速受河床冲刷影响的系数，随河床冲刷断面的增大而减小，依据工程经验对黄河青石段河床取1.02(μ为河床粒径系数，p为冲刷系数)；V1为水流流经桥下时断面平均流速，m/s；V2为上游断面平均流速，m/s；Qs为河道设计流量，m3/s；Aj为冲刷前桥下净过水面积，即桥下总过水面积与桥墩阻水面积之差，m2；AG为有限过水面积，一般为冲刷后桥下净过水面积，m2；Aj和AG的取值根据各桥尺寸分别计算。

3 实例应用与分析

3.1 研究区概况

黄河自中卫市南长滩流入宁夏回族自治区境内，至石嘴山市头道坎麻黄沟以北出境，全长397 km，流向由南偏西转为北偏东。宁夏境内河势差异明显，河段由峡谷段、库区段和平原段3部分组成，其中平原段约占2/3。平原河段具有横断面宽、水位浅、坡度缓的特点，河流水力学特性较为复杂，跨河路桥工程修筑较多。青石段内修建的跨河工程导致河道过水断面收缩，流态发生改变，上游流速减小，河流动能转化为势能，客观表现为水位壅高，洪水期内桥墩壅水给桥梁自身与岸坡及堤防造成潜在威胁，一直以来是宁夏平原区防洪影响评价的重点关注内容。

本次研究选取宁夏河段青石段内连续7座跨河桥梁作为研究对象，自上游向下游分别为青铜峡黄河大桥、古青高速公路桥(青铜峡黄河特大桥)、吴忠黄河大桥、石中高速公路桥、大古铁路桥、叶盛黄河桥(老桥)和叶盛黄河公路大桥(按先后顺序编号为1#～7#桥)，黄河研究河段地理位置以及跨河桥梁分布见图1。研究区域内建设有两座水文观测站，其中青铜峡水文站位于青铜峡水电站与青铜峡黄河大桥之间，吴忠水文站位于研究河段中部，便于研究所需长序列观测数据的获取，该河段多年连续水文与洪水数据较为完整，是进行桥梁壅水分析研究的理想区域。根据对7座跨河桥梁的相关数据的查阅和实地勘测，分别得到桥长、墩径、跨数、桥墩形状等桥梁相关设计参数，如表1所示。

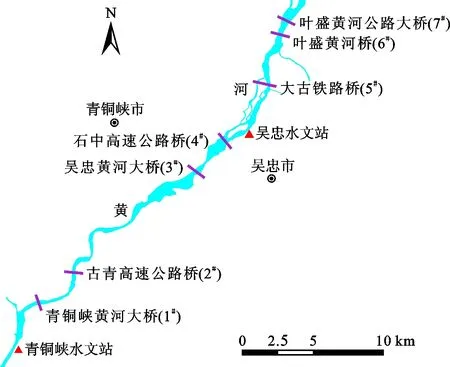
图1 黄河研究河段地理位置以及跨河桥梁分布

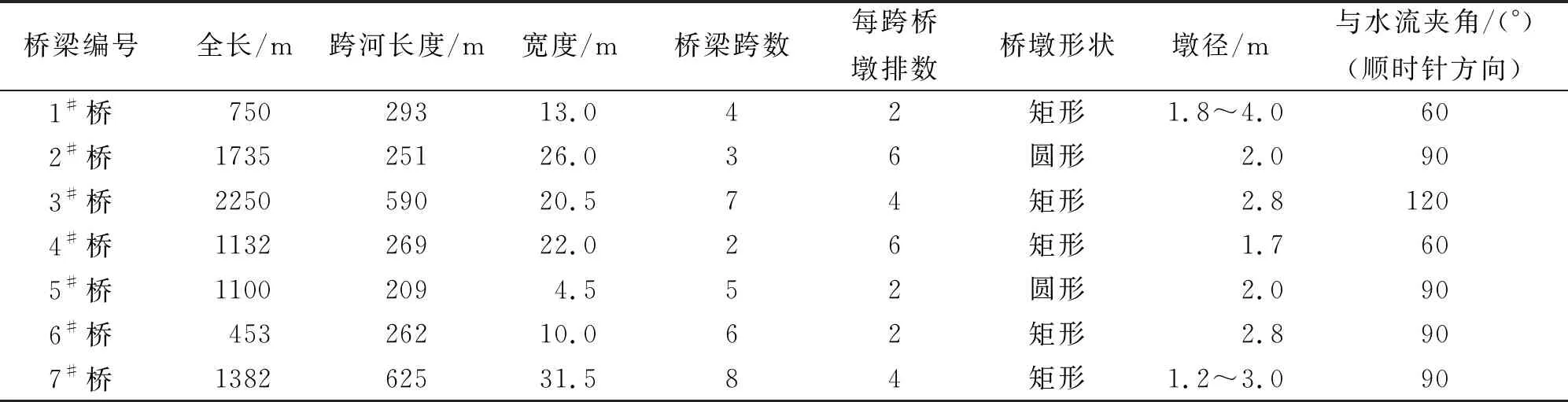
表1 选取的7座跨河桥梁相关设计参数

3.2 模型率定与验证

3.2.1 模型计算范围 二维水动力模型基于MIKE21中Flow Model模块构建，模型采用1∶10000实测地形数据，模拟范围为青铜峡水库下游至叶盛黄河公路大桥下游约300 m处，全长26.4 km。模拟计算河段地形的模型概化图见图2。

3.2.2 模型率定与验证 数值计算模型网格划分形式为三角形，网格总数为56 452个，网格边长范围为1～100 m，为保证模型计算精度，在较为复杂的边界及桥墩处采用局部加密的方式设置单元网格，并调整网格角度以减少计算误差。桥墩位置计算网格加密如图3所示。

在边界条件设置中，上游设为流量边界，下游设为水位边界。选取2008年河段实测洪水资料对水动力模型进行率定，并用2012年实测数据进行验证，2008年上游最大洪峰流量为2 280 m3/s，下游洪水水位为1 112.54 m，2012年上游最大洪峰流量为3 070 m3/s，下游洪水水位为1 116.72 m。

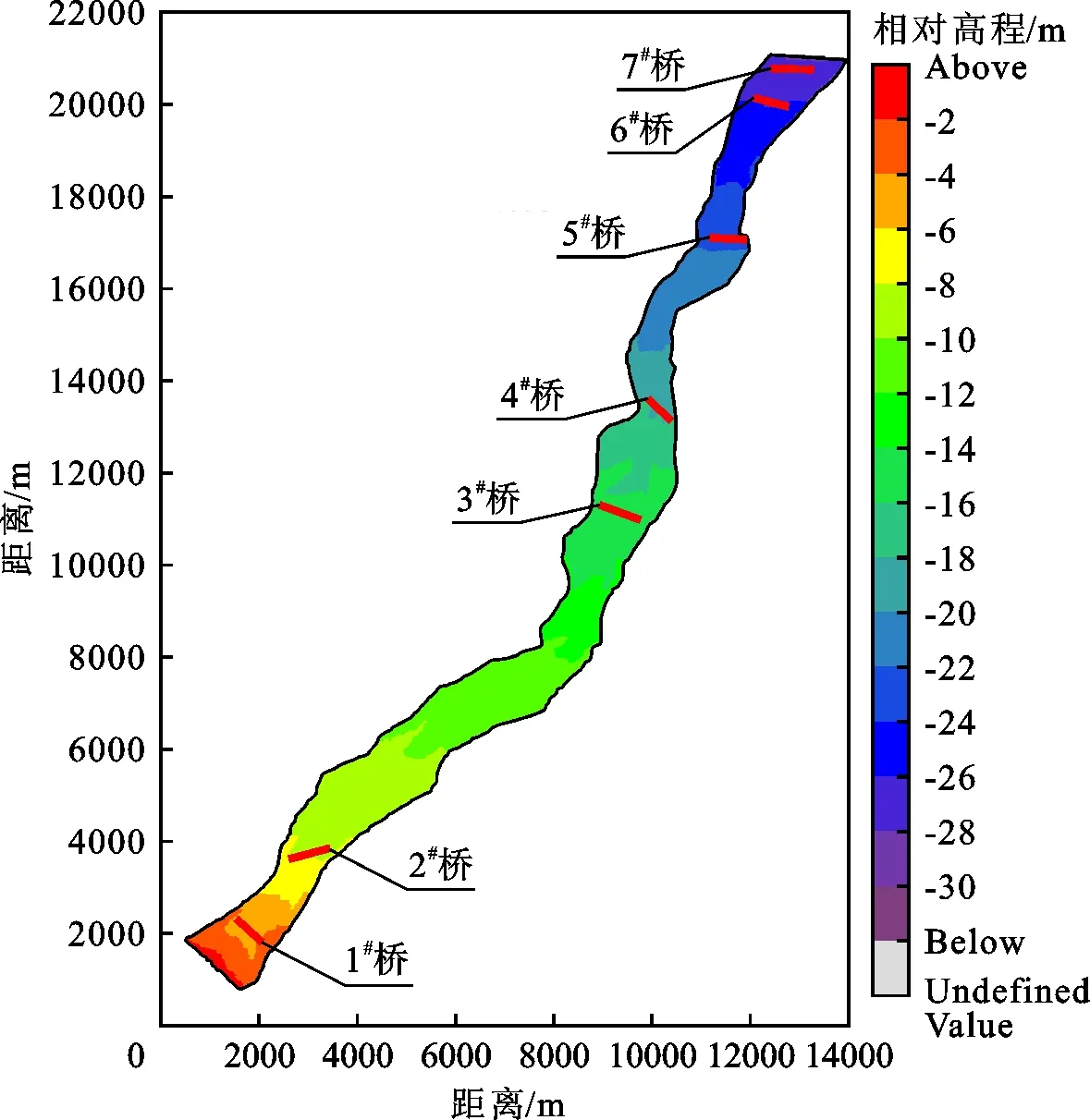
图2 黄河模拟河段模型概化图

图3 不同类型的桥墩位置模型计算网格加密示意图

桥墩影响在亚网格结构中使用拖曳理论进行计算，模拟桥墩产生的摩擦力随流速增加而发生的变化，其中设定桥墩几何形状是关键，分别在参数设置中输入桥墩形状、尺寸、个数、上游水流方向与桥墩夹角和垂向断面的分段数目。

河道糙率的选取综合考虑复杂的复式过水断面，由河道各糙率单元的影响因子综合计算得出。本次研究采用根据多年河道大断面及各断面的实测水位，通过河流动力学方法对黄河青石段综合糙率进行率定，得出其综合糙率值合理范围为0.019～0.034，主槽糙率值范围为0.015～0.030。在模型参数设置中，糙率n取值为0.025，曼宁系数m取值为40。各跨河桥梁断面河道水位模型率定结果见表2。

由表2可知，模拟水位的相对误差均小于1%，表明模拟结果可信度较高[9]，能够较好地反映河道特征。

3.3 结果与分析

3.3.1 桥梁壅水模拟计算结果 模拟计算以黄河宁夏河道多年可行性研究报告作为参考，分别选取20年一遇(P=5%)和50年一遇(P=2%)设计洪峰流量与洪水水位作为边界约束条件，上游流量控制条件分别为Q5%=5680 m3/s、Q2%=6030 m3/s，下游洪水水位分别为Z5%=1117.65 m、Z2%=1118.37 m。壅水数值模拟可直观反映出桥梁的壅水状况，计算出壅水高度，其模拟结果见图4和表3。

3.3.2 桥梁壅水经验公式计算结果 根据研究区内7座桥梁的相关资料与实测数据，分别确定Henderson经验公式与陆浩经验公式中的参数，并计算出不同洪水频率下各桥梁的壅水高度，计算结果见表4。

3.3.3 结果分析 桥梁壅水高度是河道断面形状、桥墩形状、墩距、墩径、桥下流速、河道糙率等因素综合作用的结果，模拟计算中较为全面地考虑了多因素的影响。从模型壅水计算结果来看，各桥梁不同洪水频率对应的桥墩最大壅水高度分别为：ΔZmax(5%)=0.103～0.224 m、ΔZmax(2%)=0.110～0.280 m，壅水高度均在0.10～0.28 m范围内。对比20年一遇与50年一遇频率洪水各桥梁壅水高度值发现，随着河道洪水重现期的缩短，相应洪峰流量减小，各桥梁壅水高度均有所降低，桥墩壅水变化逐渐趋于平稳。将不同洪水频率下各桥梁壅水高度的本文模拟结果、两种经验公式计算结果及实测值进行对比，见图5。

表2 各跨河桥梁断面河道水位模型率定结果

表3 不同洪水频率各桥梁的壅水高度数值模拟结果

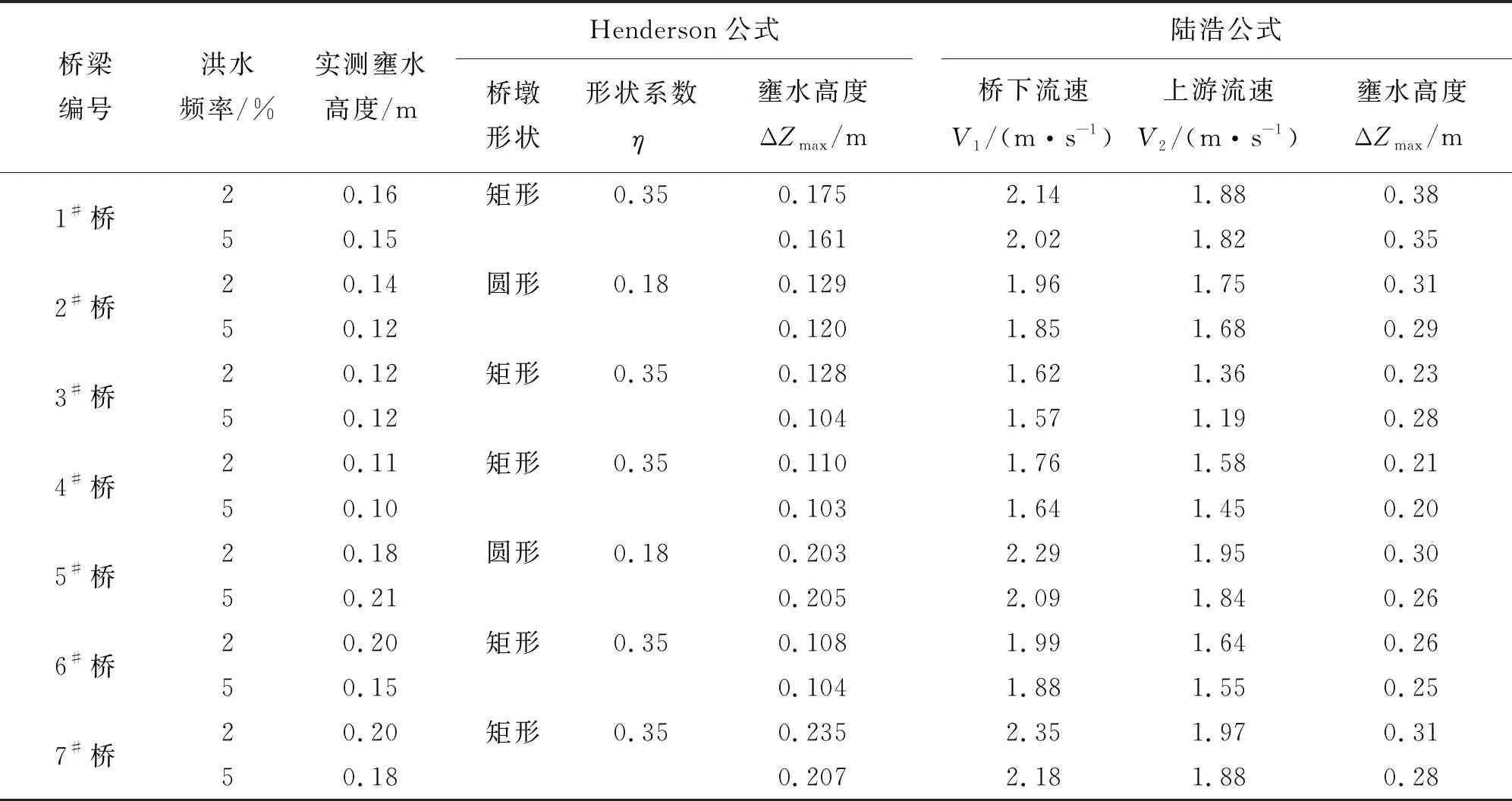
表4 不同洪水频率各桥梁的壅水高度经验公式计算结果

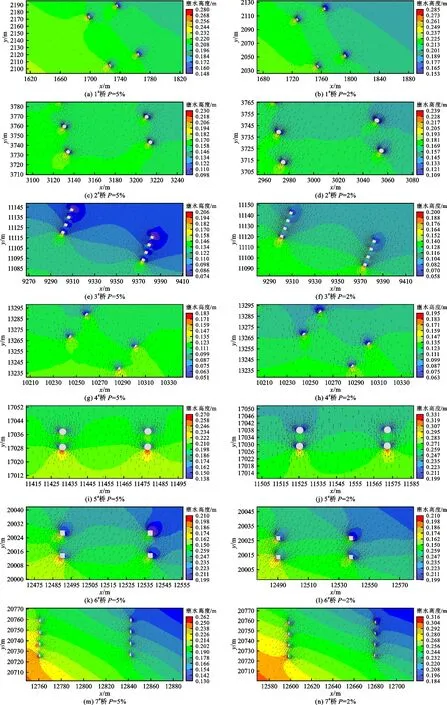
图4 不同洪水频率各桥梁的壅水状况数值模拟云图

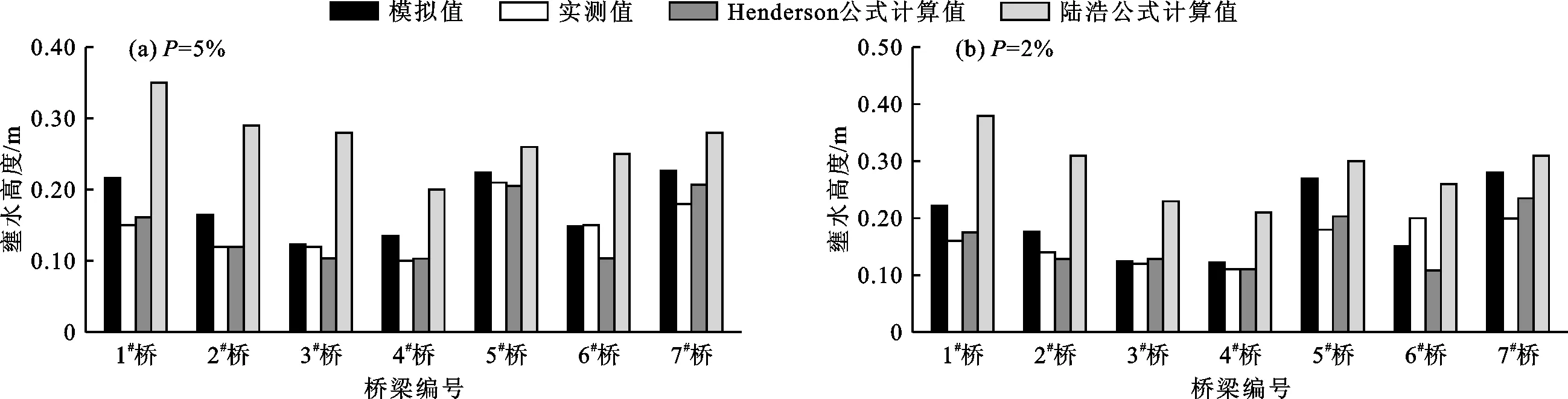
图5 不同洪水频率下各桥梁壅水高度的模拟值、经验公式计算值及实测值对比

分析图5可知：(1)由于洪水过境时桥墩周围泥沙冲淤较为明显，河床地形发生变化，导致实测壅水高度偏小，而本文模拟过程中未考虑这一影响，除6#桥外，其他桥梁的模拟壅水高度均大于实测壅水高度。(2)经验公式计算所得壅水高度与桥墩布置形式和几何形状有关，当桥下水流流速较大时，壅高水位值随之变大；各桥梁壅水高度模拟值与Henderson公式计算值均随着洪水频率P的减小而降低，二者变化趋势较为一致，在数值上各桥梁壅水高度的Henderson公式计算结果均小于模拟结果。(3)各桥梁壅水高度模拟值与陆浩公式计算值的变化趋势不完全一致，且二者数值相差较大。

根据图5分别对桥梁壅水高度的模拟值、经验公式计算值与实测值的相对误差范围进行统计，结果见表5。由表5可以看出，模拟值及Henderson公式计算结果与实测值的相对误差较小，三者数值较为接近，而陆浩公式计算结果的相对误差较大。

表5 桥梁壅水高度模拟值及经验公式计算值的相对误差绝对值范围 %

4 讨 论

本次研究桥墩壅水特性采用了数值模拟法，基于黄河青石段长序列观测数据进行了模型边界约束条件设置和河道糙率率定。从模型率定与验证结果来看，所构建的二维水动力模型能够快速、便捷地模拟研究河段内的行洪过程，较为全面地反映河道水流特性，提升了研究效率。在模拟计算过程中考虑了河道中桥墩形状、水流特性等多因素的影响，对模型参数进行了多方面设置，在一定程度上减小了因模型参数设置不全而导致的偏差，模拟结果较为理想。任梅芳等[9]对于南渡江跨河桥梁壅水特性的二维水动力模拟研究进一步验证了这一结论。需要指出的是，基于MIKE21水动力模块构建的二维数值模型均在水流为恒定流的假设下进行，未考虑实际河道中的非恒定流因素，其结果难免会产生偏差，但该数值模拟方法在进行河道复杂边界条件全面演化与桥墩水流特性分析时具有明显的优势，如王涛等[8]运用此方法得到了河道行洪模拟中桥墩壅水的可靠计算方法；吴时强等[1]采用此方法量化分析了桥群的叠加阻水效应，均取得了良好的模拟效果。

针对模拟结果进行对比分析时，本文采用的是Henderson经验公式与陆浩公式，二者各有其特点，不同学者也对其特点进行了较为全面详细的分析。Henderson经验公式基于能量方法建立，优点是形式简洁、计算方便，适用于河道糙率较大的河流，但对于河底和两岸水生植物较少、糙率较小的河道计算，存在一定的局限性。陆浩公式是利用能量守恒原理进行参数修正后所得，考虑了河床冲刷对河道壅水高度的影响，对河道坡度、地形及糙率等参数的精确性要求较高。在进行壅水高度计算时，Henderson公式考虑了桥墩形状，根据不同桥墩形状确定相关系数，其计算结果比陆浩公式更接近实际值，这也与吴泽宇等[20]的研究结论相吻合。

5 结 论

(1)本次研究选取2008年与2012年两个典型年份的水位流量数据对模型边界约束条件进行设置，根据黄河青石段长序列数据率定河道糙率，基于实测数据分别对模型进行率定与验证。从结果来看，模型参数设置合理，对河道复杂地形的模拟效果较好，模拟值与实测值相对误差均小于5%，该研究河段数值模型仿真度较好。

(2)当洪水重现期由50年一遇变为20年一遇，河道内相应设计最大洪峰流量减少，水位降低，桥墩壅水变化幅度变小且趋于平稳；两种洪水频率的水位壅高模拟值在0.10～0.28 m范围内，将模拟值及两种壅水经验公式计算结果与实测值相比较，Henderson公式计算值及模拟值与实测值的变化趋势较为一致且在数值上更为接近，而陆浩公式计算结果相对偏大。

(3)通过对桥梁壅水特性的数值模拟与对比分析，认为基于MIKE21构建的二维水动力模型在河道防洪演算方面较为适用，对实际河道的仿真模拟结果较可靠。本次模拟与计算均在假定河道水流为恒定流的条件下进行，下一步拟开展对河道非恒定流条件下的桥墩壅水研究。