基于高斯过程的航天器自适应滑模姿态控制

赵玉新，何永旭，徐庚，陈力恒

基于高斯过程的航天器自适应滑模姿态控制

赵玉新，何永旭，徐庚，陈力恒

（哈尔滨工程大学 智能科学与工程学院，黑龙江 哈尔滨 150001）

针对存在模型不确定性和外界干扰的刚性航天器，提出了一种基于高斯过程回归（GPR）的新型自适应滑模姿态控制算法。该算法具有自学习能力，在不同的姿态控制任务下都能够实现高精度、强鲁棒和高效率的姿态跟踪。首先，在航天器的四元数标称系统动态模型基础上，应用在线稀疏高斯过程回归（SOGP）方法学习系统的未知动态；其次，结合高斯过程的预测均值设计滑模控制算法，利用高斯过程的预测方差自适应调节控制增益，并应用李雅普诺夫方法严格证明闭环系统的稳定性，保证了航天器姿态跟踪误差的渐进收敛性；最后，通过数值仿真验证了所设计控制器的有效性。结果表明，该自学习控制算法与自适应滑模控制（ASMC）与神经网络自适应控制等算法相比，具有更快的收敛速度、更高的跟踪精度以及更低的控制成本。

姿态跟踪；四元数；高斯过程回归；自适应控制；滑模控制

0　引言

高精度的姿态控制是航天器成功执行巡逻、编队飞行与交会对接等任务的关键［1-3］。然而，航天器的转动惯量不确定性、外界干扰力矩以及其姿态动力学的高度非线性与强耦合性都为高精度姿态控制带来一定的难度。因此，研究存在模型不确定性和外界干扰的航天器姿态控制具有重要的实际意义。

针对航天器存在不确定性时的姿态控制问题已提出了许多非线性控制算法，如滑模控制［4］、反步法控制［5］与自适应控制［6］等。这些传统的控制算法虽然通过采用观测器或自适应算法补偿不确定性的方式提高了姿态控制的性能，但缺乏自学习的能力，在姿态跟踪任务发生变化时，若不人为调整控制参数，姿态控制的性能可能会大大降低［7］。近年来，学者们将强化学习、神经网络等机器学习方法与传统的控制算法结合，通过充分利用航天器的观测数据来有效提高姿态控制的自学习能力。文献［7］设计了基于强化学习的滑模控制算法，保证了航天器在跟踪任务变化时的控制性能。但该算法需要采集离线观测数据以确保控制参数学习的速度，增加了算法的实际应用难度。文献［8］将切比雪夫神经网络与终端滑模控制相结合，解决了航天器存在不确定性时的有限时间姿态跟踪控制问题。文献［9］设计了基于径向基神经网络的滑模控制算法，扩大了神经网络的有效作用区域，从而保证了航天器对于未知干扰的鲁棒性。由于神经网络是一种确定性的机器学习方法，难以直接评估不确定性的预测可靠性，所以神经网络控制算法通常需要采用较高的反馈增益来避免不确定性的预测误差对闭环系统控制性能的影响，使得这类算法的控制成本较高。

高斯过程回归（Gaussian Process Regression， GPR）是一种基于概率的机器学习方法，具有严格的统计学理论基础，能够有效处理高维度、小样本和非线性的复杂函数建模问题［10］。GPR方法利用高斯过程（Gaussian Process，GP）描述未知函数的分布情况，并可基于输入输出数据对函数值进行预测。GP模型为非参数模型，能够有效处理数据的观测噪声，并且其预测的可靠性可由方差信息评估［11］。因此，GPR方法也可与传统的控制算法相结合来提高不确定非线性系统的控制性能和自学习能力。文献［12］设计了基于GPR的计算力矩控制算法，通过提高不确定性的补偿精度，有效地降低了反馈控制增益，从而提高了控制效率。该方法虽然通过引入GP模型的预测方差降低了控制成本，但需要离线采集大量的训练数据以保证GP模型的有效性，所以算法的实际应用性不强。文献［13］将在线GPR方法与模型参考自适应控制相结合，避免了传统自适应控制中有关输入信号持续激励的约束。该方法对于模型不确定性的鲁棒性较强，但难以保证外界干扰存在时的跟踪控制性能。

针对具有模型不确定性且受外界干扰影响的航天器，提出了一种基于GPR的自适应滑模控制（Adaptive Sliding Mode Control，ASMC）算法，以保证不同姿态控制任务下都能够实现高精度、强鲁棒和高效率的姿态跟踪。首先，根据系统的观测数据，基于GPR方法学习不确定性的映射，从而利用GP模型的预测均值实现精准的动态补偿。然后，结合GP模型设计ASMC算法，利用预测方差主动调节反馈增益以及控制参数自适应律的更新速度，使得控制参数可根据不确定性的预测可靠程度进行自整定。最后，利用李雅普诺夫方法证明航天器的姿态与角速度跟踪误差在任意概率下都能够全局渐进收敛。通过与ASMC和神经网络滑模控制方法的仿真结果对比说明，所提出的自学习控制算法对于不同的姿态控制任务都具有更快的收敛速度、更高的跟踪精度以及更低的控制成本。

1　问题描述

那么，航天器的姿态跟踪误差运动学与动力学模型可表示为［14］

式中：

2　控制器设计

2.1　基于GPR的不确定性学习与预测

2.2　基于GPR的自适应滑模跟踪控制算法

定义滑模变量为

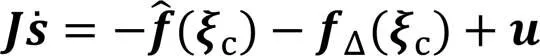
式中：

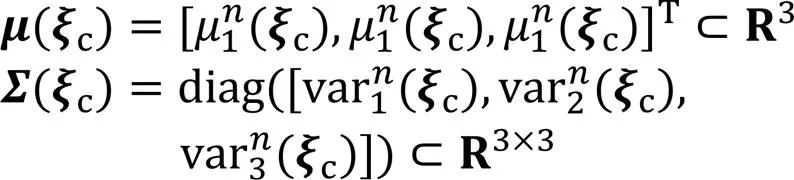
分别为预测均值向量与方差矩阵，其中各元素可根据式（12）计算得到。

针对航天器（1）的姿态跟踪控制问题，可根据式（17）、式（20）与式（22），设计以下基于GP的ASMC（GP-ASMC）算法：

3　闭环系统稳定性分析

证明 选取李雅普诺夫函数为

则根据式（29）可知

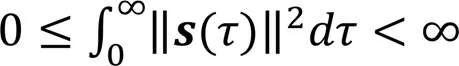
4　仿真实验与分析

本章将通过数值仿真算例说明GP-ASMC算法在航天器姿态跟踪控制应用中的有效性。仿真中令航天器惯性矩阵的真实值为

航天器初始姿态的矢量部分与初始角速度分别为

本仿真采用ASMC［6］与神经网络ASMC（Neural Network ASMC，NN-ASMC）算法［9］作为对比方法，来说明GP-ASMC算法的优越性。3种方法所采用的控制参数见表1。另外，本仿真还将在不改变控制参数的情况下令航天器执行2种不同的姿态控制任务，以验证GP-ASMC算法的自学习能力。2种姿态控制任务所对应的期望姿态参数见表2。

表1　3种控制算法的参数设置

表2　2种姿态控制任务的期望姿态参数

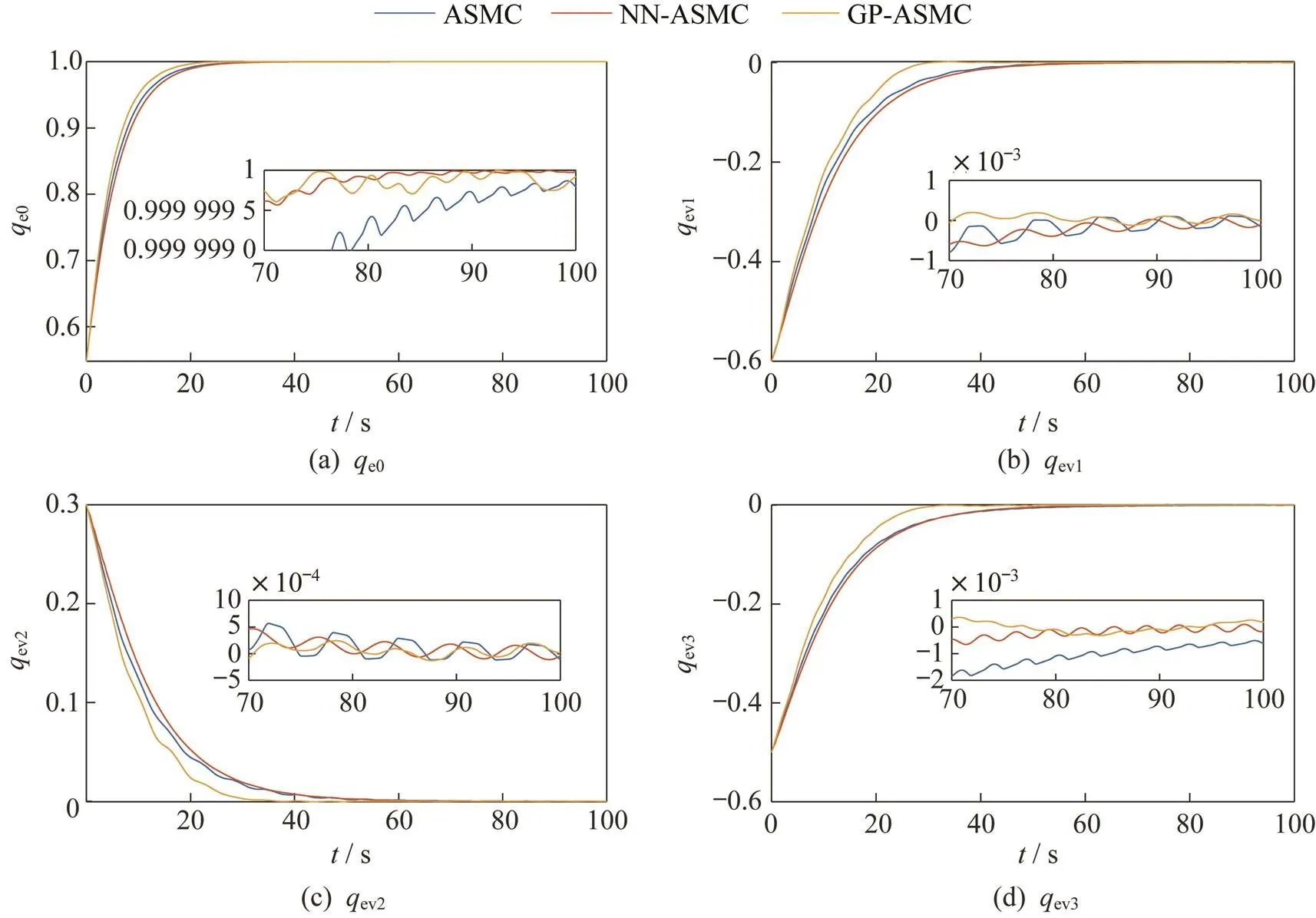
图2　任务1下的姿态四元数跟踪误差

图3　任务1下的角速度跟踪误差

图4　任务1下的控制力矩

图5　任务1下基于GP的不确定性预测

图6　任务1下的控制增益自适应更新曲线

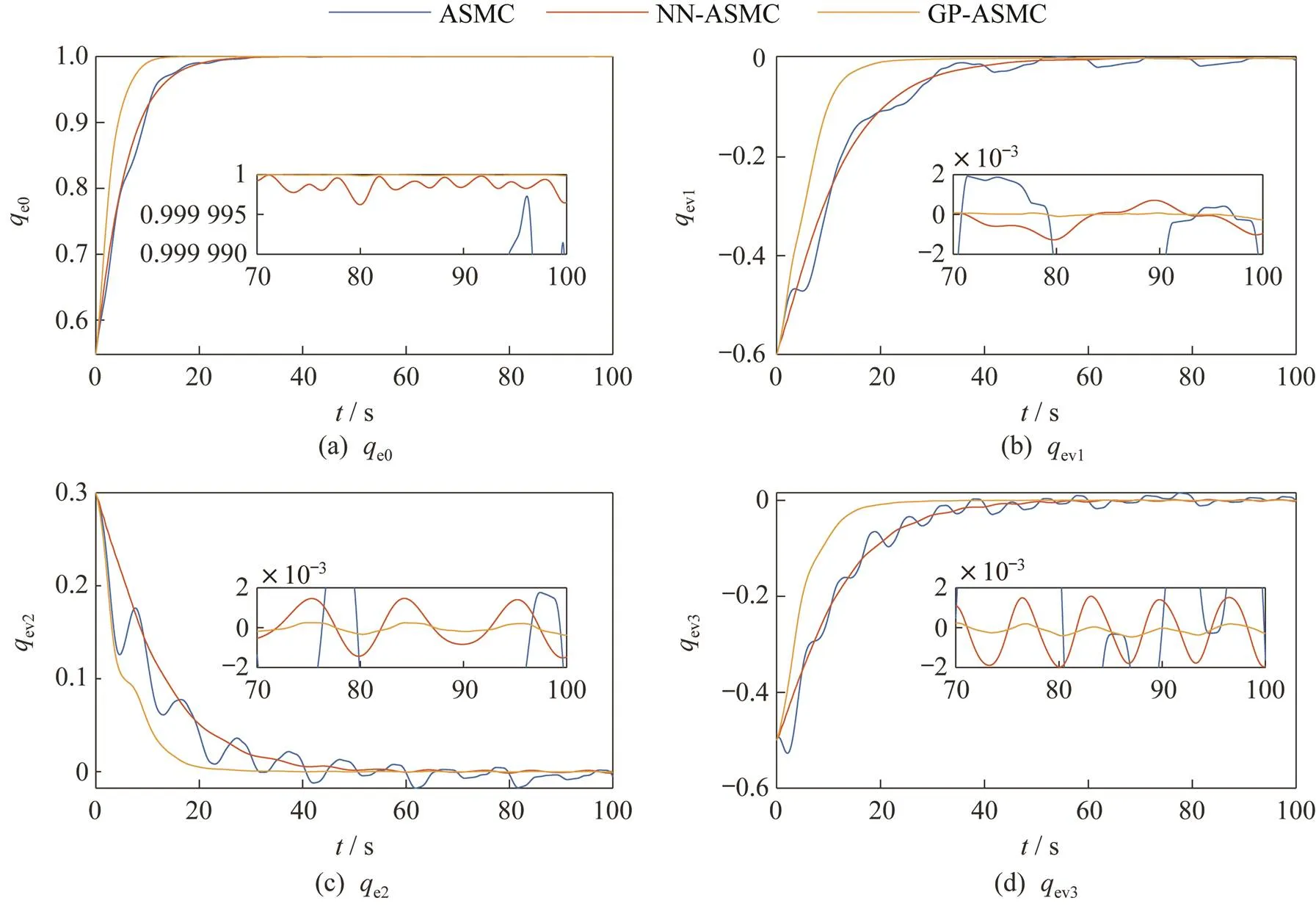
图7　任务2下的姿态四元数跟踪误差

图8　任务2下的角速度跟踪误差

图9　任务2下的控制力矩

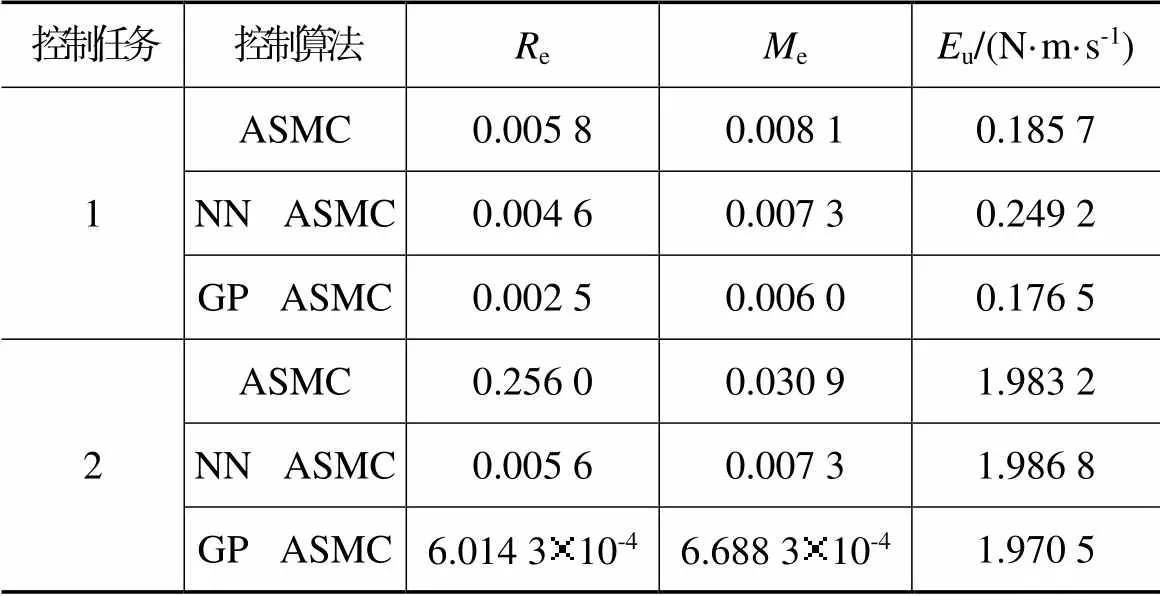
表3　3种控制算法的性能比较

5　结束语

本文针对存在较强模型不确定性且受外界干扰影响的航天器，利用GPR学习算法与滑模控制框架，设计了一种具有自学习能力的自适应滑模姿态跟踪控制算法，并证明了姿态四元数与角速度跟踪误差是全局渐进收敛的。所提出的GP-ASMC算法利用具有概率意义的GP模型学习系统的总不确定性，不仅可以利用GP预测均值实现精准的动态补偿，还可以基于预测方差调节控制增益，在保证跟踪控制精度的同时可提高算法的控制效率。另外，所应用的ASMC框架使得GP-ASMC对不确定性的预测误差具有一定的鲁棒性。仿真实验结果：GP-ASMC算法对于不同的姿态控制任务都具有收敛速度快、跟踪精度高、控制成本低的优点，具有一定的实际工程应用价值。为了进一步说明该算法对控制系统元器件误差的容忍能力，后续将分析执行机构的非线性以及传感器的量测信息缺失与量测误差等影响因素对航天器姿态跟踪性能的影响，并改进控制算法以保证其实际应用的有效性。

［1］ LIU X， MENG Z， YOU Z. Adaptive collision-free formation control for under-actuated spacecraft［J］. Aerospace Science and Technology， 2018， 79： 223-232.

［2］ NASTASI K M， BLACK J T. Adaptively tracking maneuvering spacecraft with a globally distributed， diversely populated surveillance network［J］. Journal of Guidance， Control， and Dynamics， 2019， 42（5）： 1033-1048.

［3］ SUN L. Adaptive fault-tolerant constrained control of cooperative spacecraft rendezvous and docking［J］. IEEE Transactions on Industrial Electronics， 2020， 67（4）： 3107-3115.

［4］ QIAO J， LI Z， XU J， et al. Composite nonsingular terminal sliding mode attitude controller for spacecraft with actuator dynamics under matched and mismatched disturbances［J］. IEEE Transactions on Industrial Informatics， 2020， 16（2）： 1153-1162.

［5］ ZHUANG H， SUN Q， CHEN Z， et al. Back-stepping active disturbance rejection control for attitude control of aircraft systems based on extended state observer［J］. International Journal of Control， Automation and Systems， 2021， 19（6）： 2134-2149.

［6］ ZHU Z， XIA Y，FU M. Adaptive sliding mode control for attitude stabilization with actuator saturation［J］. IEEE Transactions on Industrial Electronics， 2011， 58（10）： 4898-4907.

［7］ ZHENG M， WU Y， LI C. Reinforcement learning strategy for spacecraft attitude hyperagile tracking control with uncertainties［J］. Aerospace Science and Technology， 2021， 119： 107-126.

［8］ ZOU A， KUMAR K D， HOU Z， et al. Finite-time attitude tracking control for spacecraft using terminal sliding mode and Chebyshev neural network［J］. IEEE Transactions on Systems， Man， and Cybernetics， Part B （Cybernetics）， 2011， 41（4）： 950-963.

［9］ ZOU Y. Attitude tracking control for spacecraft with robust adaptive RBFNN augmenting sliding mode control［J］. Aerospace Science and Technology， 2016， 56： 197-204.

［10］ RASMUSSEN C E， WILLIAMS C K I. Gaussian processes for machine learning［M］. Cambridge， Mass： MIT Press， 2006： 1-83.

［11］ SRINIVAS N， KRAUSE A， KAKADE S M， et al. Information-theoretic regret bounds for Gaussian process optimization in the bandit setting［J］. IEEE Transactions on Information Theory， 2012， 58（5）： 3250-3265.

［12］ THOMAS B， DANA K， HIRCHE S. Stable Gaussian process based tracking control of Euler-Lagrange systems［J］. Automatica， 2019， 103： 390-397.

［13］ CHOWDHARY G， KINGRAVI H A， HOW J P，et al. Bayesian nonparametric adaptive control using Gaussian processes［J］. IEEE Transactions on Neural Networks and Learning Systems， 2015， 26（3）： 537-550.

［14］ SHUSTER M D. A survey of attitude representations［J］. The Journal of Astronautical Sciences，1993， 41（4）： 439-517.

［15］ YANG Y. Spacecraft modeling， attitude determination， and control quaternion-based approach［M］. CRC Press， 2019： 43-52.

［16］ SIDI M J. Spacecraft dynamics and control： a practical engineering approach［M］. New York： Cambridge University Press， 1997： 88-111.

［17］ OPPER M. Sparse online Gaussian processes［J］. Neural Computation， 2002， 14（3）： 641-669.

［18］ FIEDLER C， SCHERER C W， TRIMPE S. Practical and rigorous uncertainty bounds for Gaussian process regression［C］// Proceedings of the AIAA Conference on Artificial Intelligence. Reston， USA： AIAA Press， 2021： 7439-7447.

［19］ 钟婧佳，赵洪，佟泽友，等.基于RBF神经网络的控制器参数优化设计研究［J］.导弹与航天运载技术，2020（3）：76-80.

［20］ KRSTIC M， KOKOTOVIC P V， KANELLAKOPOULOS I. Nonlinear and adaptive control design［M］. Hoboken， USA： John Wiley & Sons， Inc.， 1995： 489-491.

Adaptive Sliding Mode Attitude Control of Spacecrafts Based on Gaussian Processes

ZHAOYuxin， HEYongxu， XUGeng， CHENLiheng

（College of Intelligent Systems Science and Engineering， Harbin Engineering University， Harbin 150001， Heilongjiang， China）

A novel adaptive sliding mode attitude control algorithm based on Gaussian process regression （GPR） is proposed for rigid spacecrafts with model uncertainties and external disturbances. The proposed algorithm has the ability of self-learning， and can always achieve attitude tracking with high accuracy， robustness， and efficiency under different attitude control tasks. First， the sparse online Gaussian process （SOGP） technique is used to learn the system unknown dynamics based on the quaternion nominal dynamic model for spacecrafts， and an SOGP technique is applied to learn the system unknown dynamics. Second， a sliding mode control algorithm is designed by using the predicted means of GPs， and the control gain is adapted based on the predicted variances. Moreover， the stability of the closed-loop system is proved by using the Lyapunov approach， which guarantees the asymptotic convergence of the attitude tracking error. Finally， the effectiveness of the designed controller is verified by numerical simulation. The results show that the proposed self-learning controller has faster convergence speed， higher tracking accuracy， and lower energy cost than the adaptive sliding mode control （ASMC） and neural network adaptive control algorithms.

attitude tracking； quaternion； Gaussian process regression； adaptive control； sliding mode control

2022‑04‑26；

2022‑06‑13

国家自然科学基金（61903098）

赵玉新（1980—），男，博士，教授，主要研究方向为水下导航技术及应用、智能控制与决策。

何永旭（1993—），女，博士研究生，主要研究方向为非线性系统控制、智能控制与决策。

TP 273

A

10.19328/j.cnki.2096⁃8655.2022.04.010