基于神经网络干扰观测器的柔性航天器姿态稳定控制

岳晓奎，吕佰梁，刘闯，韩豪泽

基于神经网络干扰观测器的柔性航天器姿态稳定控制

岳晓奎1，2，吕佰梁1，2，刘闯1，2，韩豪泽1，2

（1.西北工业大学 航天学院，陕西 西安 710072；2.西北工业大学 航天飞行动力学技术重点实验室，陕西 西安 710072）

本文针对柔性航天器在惯性参数未知、外界干扰、输入饱和等复杂条件下的姿态控制问题，提出了1种基于神经网络干扰观测器的柔性航天器姿态稳定控制方法。首先，基于包含压电振动抑制输入的柔性航天器姿态动力学模型，构建了包含外界干扰、惯性参数不确定性的综合扰动项；其次，基于RBF神经网络设计干扰观测器与自适应参数调节律实时地估计综合扰动；再次，设计了1种固定时间收敛且有限时间稳定的非线性滑模控制器，并通过Lyapunov理论进行了稳定性分析；最后，利用航天器闭环姿态动力学系统进行数值仿真。结果表明：所设计的基于神经网络干扰观测器的控制方法可以有效实现航天器的姿态稳定、振动抑制与干扰估计，从而顺利完成航天器的高精高稳控制任务。

柔性航天器；神经网络干扰观测器；固定时间收敛；有限时间稳定；姿态控制

0　引言

航天器高精度姿态控制技术作为未来空间发展与应用的前提和基础，相关研究近年来受到了众多学者的广泛关注。由于航天器通常携带太阳能帆板、大型天线等柔性附件，在刚性本体与柔性附件之间会产生非线性刚柔耦合效应，给柔性航天器的姿态稳定与振动抑制带来巨大挑战［1］。为了克服该问题，众多学者对一系列柔性航天器的姿态控制分析方法进行创新，例如，滑模控制［2］、鲁棒控制［3］、反步控制［4］、自适应控制［5］以及复合控制［6］等。

针对柔性航天器的姿态跟踪控制问题，HU等［7］提出了1种模型自由的预设性能控制方法，但并未考虑对柔性附件的振动模态进行处理，稳定状态下航天器存在较大的模态振动。朱锐等［8］针对带有震荡液体的柔性航天器姿态机动问题，提出了1种综合正弦型加速度与云多目标粒子群算法的快速路径规划与多目标优化控制方法，但整个过程的计算较大，现有的星载计算机难以实现。MIAO等［9］提出了1种快速自适应非奇异滑模控制器，实现柔性航天器高精度姿态跟踪控制，但对于低阶模态没有良好的振动抑制效果。赵真等［10］针对空间站太阳帆板高精度对日定向问题，基于完整的动力学建模、分析与规划，提出了1套内外环滤波器与振动抑制相结合的复合控制框架，实现了柔性太阳帆板的高精高稳控制，且具有良好的控制效果。刘闯等［11］利用分布式压电执行器，进行柔性附件的主动振动抑制，并在线性化假设条件下，提出了1种考虑输入幅值和变化率约束的、基于状态干扰协同观测的鲁棒控制策略，有效地实现了针对在轨捕获后柔性组合体的高精高稳控制。张秀云等［2］提出了1种综合输入成形、自适应有限时间干扰观测器、有限时间积分滑模控制器的控制策略，并取得了良好的控制效果，但整个设计过程较为复杂。

随着计算机技术的发展，基于神经网络的智能控制方法在航天器控制领域取得了大量的研究成果［12-13］。在轨运行航天器会不可避免地受到例如太阳光压、重力梯度力矩、大气阻力力矩等外界干扰的作用，如不加以处理，可能会导致航天器的姿态失稳，控制系统无法正常运行，甚至航天任务的失败［14］。基于干扰观测的控制器设计方法能够实时地估计与补偿外界干扰，在干扰抑制方面取得了良好的效果［15］，但依赖于对于外界干扰的假设，这些假设在某些工作条件下是无法满足的。由于神经网络具有对未知信息良好的在线学习与估计拟合能力，且不依赖于其他先验假设条件，李正楠等［16］将其应用于多关节机械臂控制，实时地拟合建模误差导致的不确定性项，并进行反馈补偿使得控制时效性与精度得到了有效提升。HUO等［17］面向刚体航天器姿态控制问题提出了1种基于神经网络干扰观测器的自适应控制方法，但稳定精度仍有待提高。PENG等［18］利用神经网络干扰观测器和动态滑模面设计技术，提出了1种针对电动机械臂的鲁棒自适应反步控制器，并利用Lyapunov方法分析了闭环系统的有界稳定性。

综上所述，基于智能控制的柔性航天器姿态稳定与振动抑制相关研究较少，如何实现其高精高稳控制仍是一个开放性问题，在存在惯性参数不确定性、外界干扰、输入饱和等多源复杂扰动时，进一步加大了控制器的设计难度。

本文提出了1种基于神经网络干扰观测器的柔性航天器姿态稳定控制方法。首先，利用径向基函数（Radial Basis Function，RBF）神经网络设计了 1种干扰观测器，实现干扰的实时估计与补偿，通过自适应律在线调节神经网络内部参数，与传统的干扰观测器相比，无需关于扰动的相关假设条件与扰动的先验信息，即可实现高精度的在线估计；其次，利用所获取的干扰估计值，设计了1种固定时间收敛、有限时间稳定的滑模控制器，相较于传统的有限时间控制，拓宽了应用条件，提高了控制效率，在柔性航天器高精高稳姿态控制方面，取得了良好的控制效果。

1　数学模型的建立

柔性航天器姿态运动学方程形式如下：

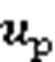
实际在轨运行航天器的姿态控制通常是利用磁力矩器、推力器、飞轮等执行机构实现的，但所能提供的控制力矩是有限的，当超出其控制范围时，执行机构只能按照饱和阈值提供控制输入，即输入饱和如下：

2　基于神经网络干扰观测器的稳定控制器设计

2.1　RBF神经网络干扰观测器设计

在实际系统中，综合干扰难以精确测量，需采用干扰观测器实时进行干扰估计与补偿，以实现柔性航天器高精度姿态稳定与振动抑制。RBF是1种具有良好局部非线性近似的神经网络，可以任意精度逼近任意连续函数，因此设计基于RBF神经网络的智能干扰观测器，实现扰动的估计重构。

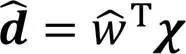
由式（6）和式（7）可得干扰估计误差

2.2　控制器设计

滑模控制是1种广泛应用于航天器控制领域的控制方法，对于被控对象参数变化、不确定性和外界干扰等因素均有一定的鲁棒性，以保证系统达到期望的性能要求。本文采用了1种新颖的在能达阶段固定时间收敛至滑模面，在滑动阶段有限时间稳定至0附近小领域的滑模控制方法，具体方式为

首先，选择滑模面

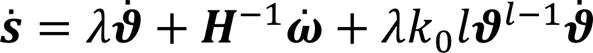
选择趋近律

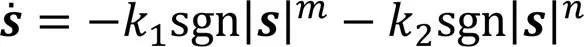
可以得到如下控制律：

2.3　稳定性分析

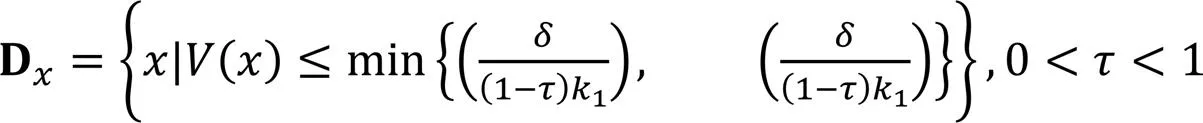
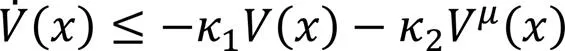
系统有限时间稳定，且稳定时间满足

定理1 针对柔性航天器姿态动力学系统（4），基于滑模面（10）和RBF神经网络干扰观测器（7）设计得到滑模控制器（14），可使得闭环系统在固定时间收敛至滑模面、在有限时间稳定到0附近的1个小邻域内，实现柔性航天器的姿态稳定与振动抑制。

证明：首先，证明系统状态在固定时间收敛至滑模面。

选择Lyapunov函数

代入式（8），可得：

由引理3可得：

由引理1可知，闭环系统在固定时间收敛到滑模面。

其次，证明到达滑模面后，系统状态在有限时间收敛到0附近。

对式（24）求一阶导得：

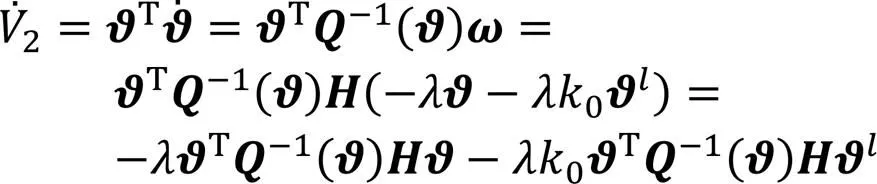
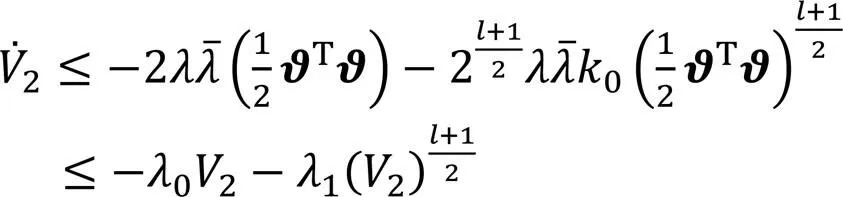
由引理2可知，系统状态收敛于滑模面后，能够在有限时间内稳定在平衡点附近的小邻域。

3　仿真试验及结果分析

3.1　仿真结果

本节基于柔性航天器闭环姿态动力学，利用所设计的控制器进行数值仿真，验证所提出方法的有效性。航天器的动力学参数见表1。

表1　柔性动力学参数

选择柔性航天器初始状态：

可以得到如图2～图7所示的仿真结果。

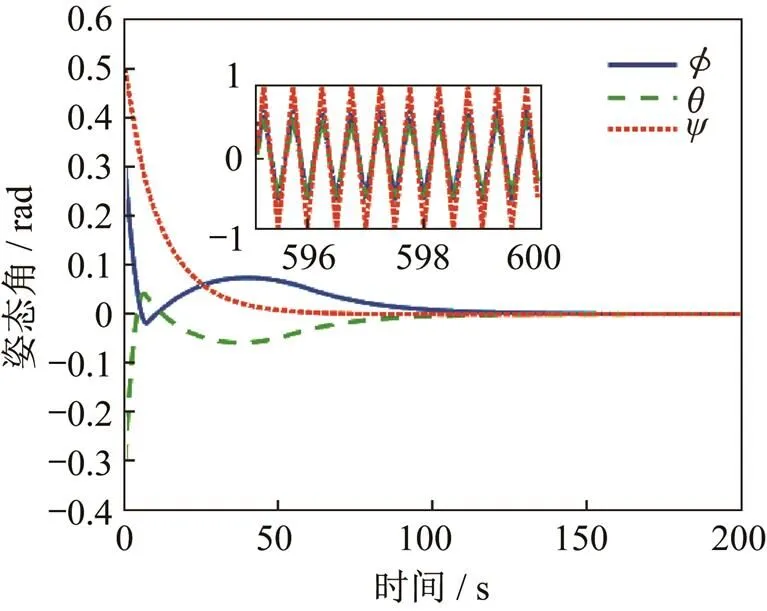
图2　姿态角变化曲线

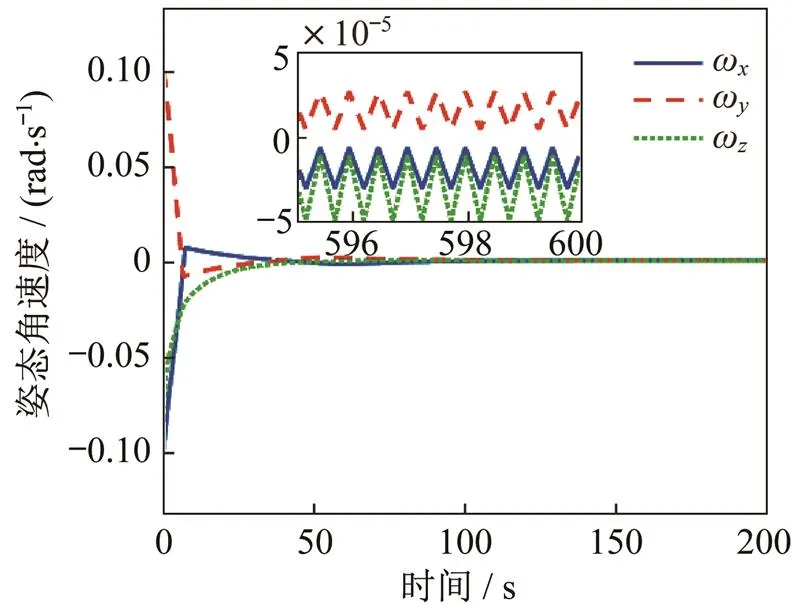
图3　姿态角速度变化曲线

图4　模态位移变化曲线

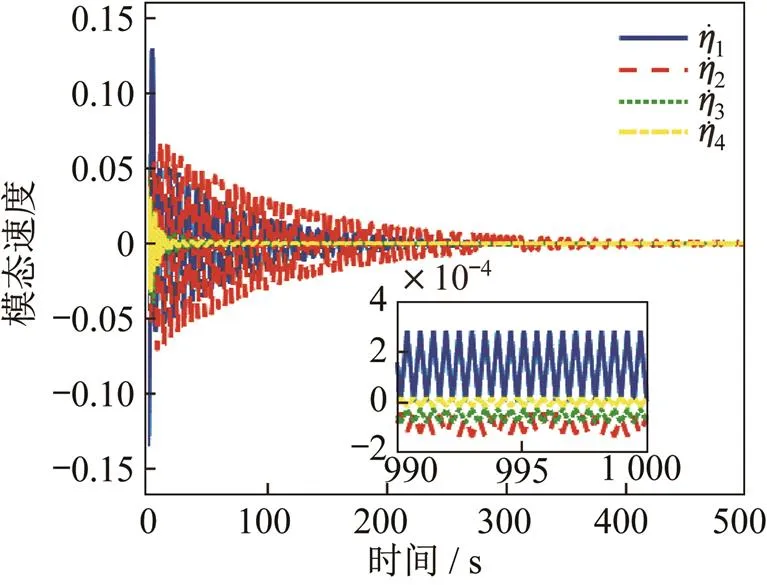
图5　模态速度变化曲线

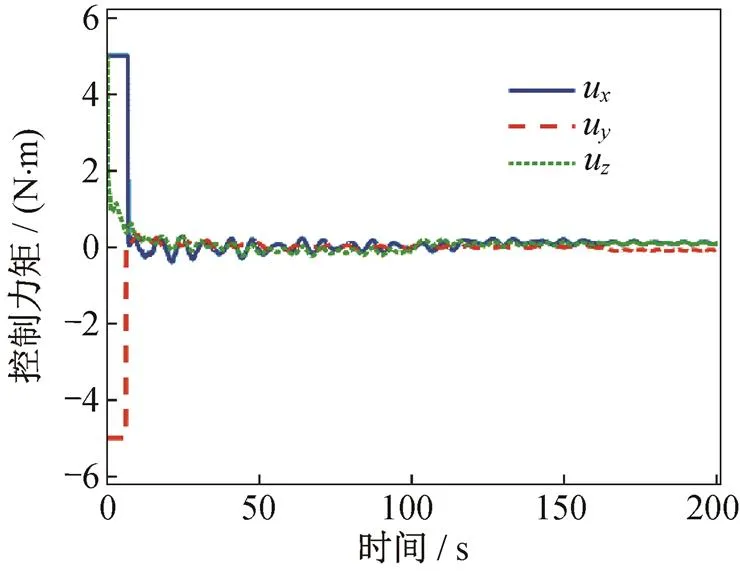
图6　控制力矩变化曲线

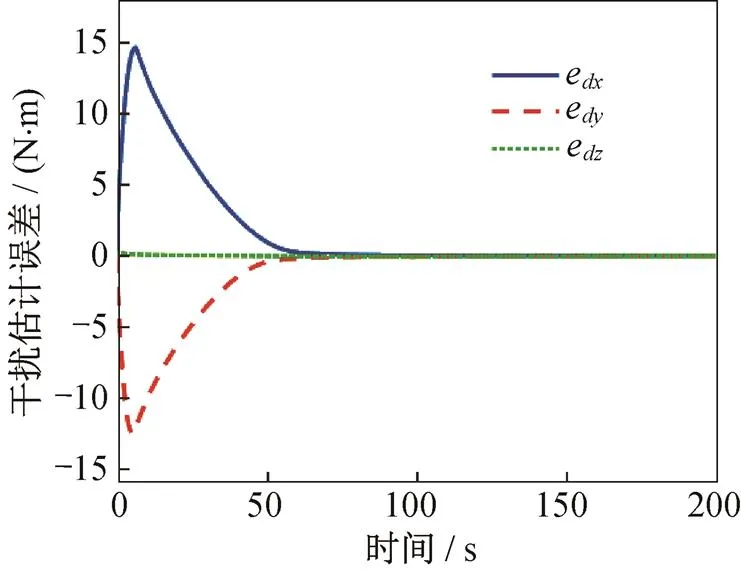
图7　干扰估计误差变化曲线

图8　姿态角范数指标对比曲线

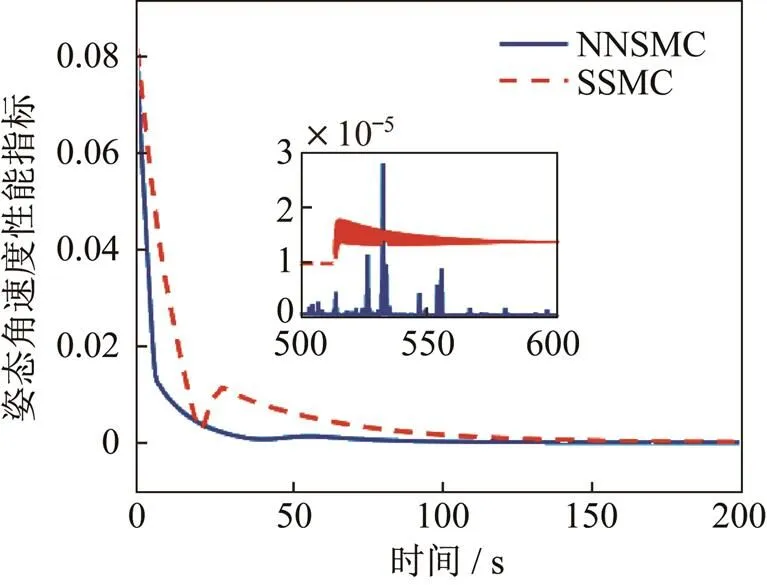
图9　姿态角速度范数指标对比曲线

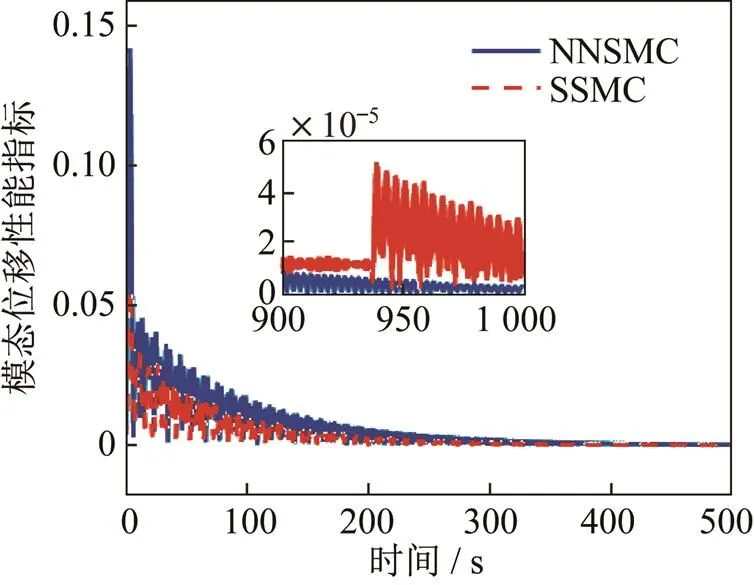
图10　模态位移范数指标对比曲线

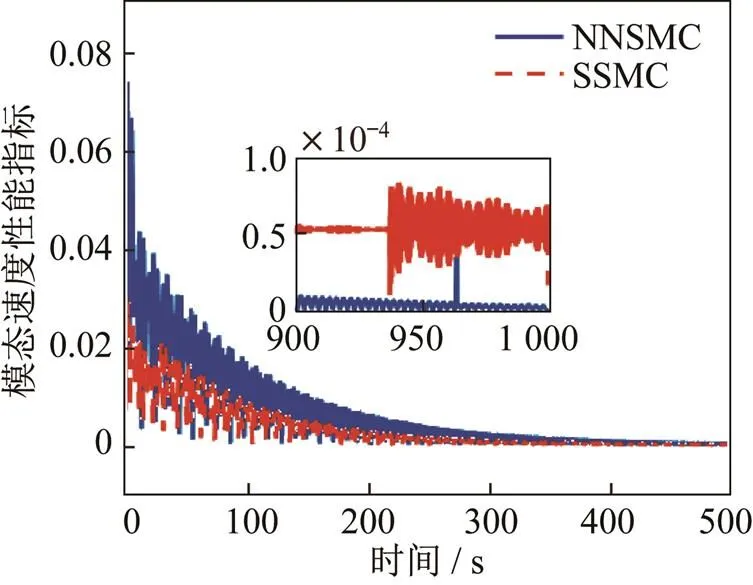
图11　模态速度范数指标对比曲线

3.2　结果分析

图2～图5描述了在基于神经网络干扰观测器的滑模控制器作用下，柔性航天器姿态动力学系统的变化曲线。图2和图3描述了柔性航天器姿态角和姿态角速度的变化特性，在较大初始状态下姿态角大约在100 s收敛到0附近的小邻域内，姿态角速度大约在 50 s左右收敛到较小范围内，再逐步稳定。当航天器逐步趋于稳定时，姿态角的稳定精度小于1×10-6rad，姿态角速度的稳定精度小于5×10-5rad/s。

图4和图5描述了柔性航天器振动模态和模态速度的变化特性，在非零初始状态下，振动模态及模态速度大约在300 s左右全部收敛到较小的范围内，并在其中震荡波动，三阶和四阶模态具有较快的收敛速度，大约在30 s左右收敛，而一阶、二阶模态收敛速度较慢，收敛过程需经过大幅震荡。稳定状态下，一阶和二阶模态的稳定精度小于1×10-5，三阶和四阶模态的稳定精度小于2×10-6，一阶、二阶的模态速度小于4×10-4，三阶和四阶的模态速度小于8×10-5。

图6和图7描述了控制力矩的变化曲线。控制力矩在输入饱和最大力矩不超过5 N·m的约束条件下，能够满足控制任务的需求，使系统达到稳定状态。图7描述了基于神经网络干扰观测器的观测误差曲线，根据所设计的神经网络与自适应律，观测误差逐步减小直至收敛到0附近，干扰估计值近似于真值，表明所设计的观测器具有良好的干扰估计效果。

图8～图11描述了NNSMC和SSMC在姿态角、姿态角速度、模态、模态速度等方面的对比仿真变化曲线。从对比仿真结果可以发现，对于姿态角及姿态角速度NNSMC相比于SSMC具有更为光滑的收敛变化曲线，超调量较小，能够满足更快速收敛的性能要求；且在稳定状态下，由于神经网络干扰观测器的高精度估计与补偿效果，NNSMC控制效果远高于SSMC且具备更好的抗抖振能力。在对于振动模态及模态速度，NNSMC收敛时间与SSMC基本相同，但在收敛过程中振动更为明显，相比于SSMC依靠自身鲁棒性抵抗干扰的作用，NNSMC可利用神经网络干扰观测器实现实时的控制补偿，因此具有更高的稳定精度。

由上述仿真结果，可以验证在惯性参数不确定性、外界干扰、输入饱和等复杂情形的共同作用下，所设计的基于神经网络干扰观测器的柔性航天器滑模控制器，在航天器姿态稳定、振动抑制与干扰估计方面的有效性，实现了高精高稳的柔性航天器姿态控制。

4　结束语

本文研究了在惯性参数未知、外界干扰、输入饱和等复杂情形下，柔性航天器的高精度姿态控制问题。首先，基于利用压电输入实现主动振动抑制的柔性航天器动力学模型，将惯性参数不确定性作为扰动项与标称参数分离，进而与外界干扰结合构建综合扰动项；其次，利用RBF神经网络设计干扰观测器，基于参数自适应律在线进行干扰估计，设计固定时间收敛、有限时间稳定的滑模控制器，进行航天器的姿态稳定控制与干扰补偿抑制；最后，实现了柔性航天器的高精高稳姿态控制与振动抑制。但本文未考虑实际在轨运行过程中航天器的轨道-姿态-模态耦合作用、执行机构故障、部分信息未知的约束情形，因此后续研究将考虑轨道-姿态-振动一体化柔性航天器抗干扰容错控制相关技术问题。

［1］ 刘付成，朱东方，黄静.空间飞行器动力学与控制研究综述［J］.上海航天，2017，34（2）：1-29.

［2］ 张秀云，宗群，窦立谦，等.柔性航天器振动主动抑制及姿态控制［J］.航空学报，2019，40（4）：238-247.

［3］ LIU C， YUE X， YANG Z. Are nonfragile controllers always better than fragile controllers in attitude control performance of post-capture flexible spacecraft？［J］. Aerospace Science and Technology， 2021， 118： 107053.

［4］ LIU Q， LIU M， DUAN G. Adaptive fuzzy backstepping control for attitude stabilization of flexible spacecraft with signal quantization and actuator faults［J］. Science China Information Sciences， 2021， 64（5）： 1-16.

［5］ 马亚杰，姜斌，任好.基于最小特征值的挠性航天器执行器故障自适应补偿技术［J］.中国科学：信息科学， 2021，51（5）：834-850.

［6］ XING L， ZHANG J， LIU C， et al. Fuzzy-logic-based adaptive event-triggered sliding mode control for spacecraft attitude tracking［J］. Aerospace Science and Technology， 2021，108： 106394.

［7］ HU Y， GENG Y， WU B， et al. Model-free prescribed performance control for spacecraft attitude tracking［J］. IEEE Transactions on Control Systems Technology， 2020， 29（1）： 165-179.

［8］ 朱锐，郭毓，王璐，等.充液挠性航天器姿态机动控制的多目标优化［J］.上海航天（中英文），2020，37（1）：11-17.

［9］ MIAO Y， HWANG I， LIU M， et al. Adaptive fast nonsingular terminal sliding mode control for attitude tracking of flexible spacecraft with rotating appendage［J］. Aerospace Science and Technology， 2019， 93： 105312.

［10］ 赵真，王碧，钱志源，等.空间站柔性太阳电池翼对日跟踪控制［J］.上海航天（中英文），2021，38（5）：31-40.

［11］ 刘闯，岳晓奎.空间非合作航天器抓捕后姿态抗干扰控制［J］.航空学报，2021，42（11）：290-306.

［12］ ZHAO L， YU J， CHEN X. Neural-network-based adaptive finite-time output feedback control for spacecraft attitude tracking［J］. IEEE Transactions on Neural Networks and Learning Systems， 2010， 21（9）：1457-1471.

［13］ LIU Y， CHEN X， WU Y， et al. Adaptive neural network control of a flexible spacecraft subject to input nonlinearity and asymmetric output constraint［J］. IEEE Transactions on Neural Networks and Learning Systems， 2021：3072907.

［14］ LIU C， YUE X， ZHANG J， et al. Active disturbance rejection control for delayed electromagnetic docking of spacecraft in elliptical orbits［J］. IEEE Transactions on Aerospace and Electronic Systems， 2022， 58（3）：2257-2268.

［15］ SUN L， ZHENG Z. Disturbance-observer-based robust backstepping attitude stabilization of spacecraft under input saturation and measurement uncertainty［J］. IEEE Transactions on Industrial Electronics， 2017， 64（10）： 7994-8002.

［16］ 李正楠，殷玉枫，张锦，等.多关节机械臂反演滑模神经网络干扰观测器控制［J］.机械设计，2021，38（3）：126-131.

［17］ HUO J， MENG T， JIN Z. Adaptive attitude control using neural network observer disturbance compensation technique［C］// 2019 9th International Conference on Recent Advances in Space Technologies （RAST）. Washington D.C.， USA： IEEE Press， 2019： 697-701.

［18］ PENG J， DING S， DUBAY R. Adaptive composite neural network disturbance observer-based dynamic surface control for electrically driven robotic manipulators［J］. Neural Computing and Applications， 2021， 33（11）： 6197-6211.

［19］ 姚晓成，赵程，曾涛.压电材料在振动控制领域的研究进展与应用现状［J］.机械工程材料，2019，43（6）：72-76.

［20］ CAO L， XIAO B， GOLESTANI M， et al. Faster fixed-time control of flexible spacecraft attitude stabilization［J］. IEEE Transactions on Industrial Informatics， 2019， 16（2）： 1281-1290.

［21］ 黄成，王岩，邓立为.航天器姿态大角度机动有限时间控制［J］.宇航学报，2020，41（8）：1058-1066.

Neural Network Disturbance Observer-Based Attitude Control for Flexible Spacecrafts

YUEXiaokui1，2， LYUBailiang1，2， LIUChuang1，2， HANHaoze1，2

（1.School of Astronautics， Northwestern Polytechnical University， Xi’an 710072， Shaanxi， China； 2.National Key Laboratory of Aerospace Flight Dynamics， Northwestern Polytechnical University， Xi’an 710072， Shaanxi， China）

A neural network disturbance observer-based attitude control strategy for flexible spacecrafts is proposed to solve the attitude control problems such as inertial parameter uncertainties， external disturbance， and input saturation. First， a lumped disturbance term including external disturbance and inertial parameter uncertainties is constructed based on the attitude dynamic model for flexible spacecrafts with active vibration suppression. Second， the lumped disturbance is estimated accurately in real time by means of the observer designed by the radial basis function （RBF） neural network and the adaptive parameter regulation law. Third， a sliding mode controller is designed to stabilize the system. It is proved by the Lyapunov theory that with the designed controller， the system states converge to the sliding mode surface at fixed-time and then stabilize in finite-time. Finally， numerical simulations of a flexible spacecraft attitude control system are performed to demonstrate the effectiveness of the proposed control strategy. The results show that the designed attitude control strategy has good performances in attitude stabilization， vibration suppression， and disturbance estimation， and can successfully complete high-precision and high-stability space control missions.

flexible spacecraft； neural network disturbance observer； fixed-time convergence； finite-time stabilization； attitude control

2022‑04‑06；

2022‑05‑31

国家自然科学基金（11972026，U2013206）；国防科技重点实验室基金（6142210200310）；广东省基础与应用基础研究基金（2021A1515110539）

岳晓奎（1970—），男，博士，教授，主要研究方向为航天动力学与控制、空间机动与智能操控。

刘闯（1990—），男，博士，副教授，主要研究方向为航天器姿态动力学与控制、鲁棒控制。

TN 964.3； V 448.2

A

10.19328/j.cnki.2096⁃8655.2022.04.006