基于高斯过程回归的组合体航天器姿态接管学习控制
马广富,刘昱晗,吕跃勇,郭延宁
基于高斯过程回归的组合体航天器姿态接管学习控制
马广富,刘昱晗,吕跃勇,郭延宁
(哈尔滨工业大学 控制科学与工程系,黑龙江 哈尔滨 150001)
空间非合作目标一般具有结构复杂、质量特性未知、姿态机动能力不明等特点,这导致组合体航天器姿态动力学呈现出高度非线性和强耦合特性,且难以对其进行在轨精确辨识。针对组合体航天器姿态接管过程中目标信息不完全、精确辨识困难等问题,本文考虑目标存在姿态机动能力的任务场景,提出了一种基于稀疏高斯过程回归(GPR)的数据驱动姿态接管控制策略。首先,从系统运行数据中提取、凝炼模型未知部分的输入/输出映射关系,构建数据驱动的概率化模型以代替无法快速准确建立的参数辨识模型,并根据该数据驱动模型设计变增益反馈控制策略,证明了系统状态概率意义上的Lyapunov稳定性和有界性;其次,考虑到在轨任务的实时性、星载计算机的计算资源有限等因素,该算法可在保证控制精度的同时显著减轻学习算法的计算压力;最后,数值仿真验证了本文所提出控制方法的有效性与实用价值。
组合体航天器;姿态接管;非合作目标;高斯过程;学习控制
0 引言
随着航天技术的高速发展,在轨服务任务也日趋多样化和复杂化。通过服务航天器对目标进行有效姿态接管操控是后续在轨加注、在轨维修、碎片清除等任务的基础[1-3]。我国国务院2016年公布的“十三五”规划中提出,将在轨服务与维护系统列为“科技创新2030”16个重点项目之一,计划于2030年前突破该项技术,保障航天器在轨安全可靠运行,迎接“太空经济”时代的到来。
目前对于传统的合作目标的接管控制技术已十分成熟,并已实现了在轨应用,如美国的轨道快车计划、欧洲的ATV[4]项目、日本的ETS-VII[5]、我国的神舟系列飞船与天宫对接[6]等。而针对空间非合作目标的接管控制,抓捕后形成的组合体航天器实际上是一个结构复杂、参数众多、耦合度高,且整体结构、质量特性均不确定的非线性系统。常规的接管控制方法一般分为2种:先辨识再控制、考虑模型不确定性的自适应控制。如文献[7-8]首先建立了组合体系统的动力学模型,并基于干扰观测器估计了末端作动器与目标之间的接触力,最后引入阻抗控制使得抓捕后形成的组合体姿态镇定。文献[9]在考虑组合体系统的惯量辨识误差以及可能存在的执行机构随机误差,在反馈控制律中引入对偏差和输入不确定性的自适应补偿项,并形成了一套自适应容错姿态接管控制方案。ZHAO[10]研究了考虑外界干扰和输入饱和情况下的组合体转动惯量参数辨识,并设计了基于同时学习的自适应有限时间控制器以实现期望轨迹跟踪。文献[11]基于RBF神经网络,分别构建了故障检测观测器和干扰补偿观测器以抵抗外界干扰、非线性不确定性以及星载传感器故障带来的负面影响。CHEN[12]针对航天器姿态动力学模型不确定或完全未知的情况,提出了一种自适应模糊估计算法对模型中未知部分进行逼近,并进一步结合2/∞方法设计了姿态控制律。
然而,转动惯量能够精确辨识的前提是整个组合体需处于空间自由漂浮状态且无外力矩输入,因此不适用于目标存在姿态机动的任务场景。另外,自适应控制方法通常在证明过程中假设模型不确定性、外界干扰等存在上界以保证闭环系统的稳定性,这对组合体航天器的姿态接管任务来说是一种过于保守的假设条件。同时,基于神经网络、模糊规则等参数化方法对模型不确定性逼近具有结构复杂、基函数选取仍然依赖模型信息的缺陷。总的来说,针对结构复杂、质量特性未知、姿态机动能力不明的空间非合作目标的接管操控任务极具挑战性并亟待解决。
近年来,随着人工智能理论的飞跃式发展,基于机器学习的控制方法以工程易实现且不依赖复杂系统模型而得到了广泛的应用。其中,高斯过程回归(Gaussian Process Regression, GPR)[13]作为一种典型的贝叶斯非参数化数据驱动建模方法,具有从系统输入输出数据中提取和凝炼模型知识的能力,并已应用于机器人控制[14]、四旋翼控制[15]、轨道预测[16]和太阳电池阵基频分析[17]等。与其他参数化学习方法相比,高斯过程(Gaussian Process, GP)的预测输出具有概率性意义,既可得到激励信号对应的模型响应均值,也可获取模型响应的方差(即预测的不确定性),2种输出均可应用于控制算法的设计,有效提高算法的鲁棒性。因此,针对目标存在姿态机动能力的组合体航天器姿态接管控制问题,设计基于GPR的学习控制策略值得深入探讨。
基于上述分析和讨论,本文重点研究考虑目标存在未知姿态机动的情况下的组合体航天器姿态接管学习控制策略。首先在服务航天器姿态先验模型基础上,基于GPR理论从系统输入/输出数据构建模型未知部分的数据驱动概率化模型。进而,考虑到学习算法的在轨运算压力,采用变分推理方法将GPR模型稀疏化,并根据该稀疏模型设计变增益反馈控制策略。最后,给出了所提出控制策略的稳定性和收敛性证明。
1 数学模型和问题描述
1.1 组合体航天器姿态模型
本文考虑的组合体航天器包括3个部分:服务航天器、目标航天器和机械臂,其几何构型如图1所示,其中,抓捕部位为目标星的星箭对接环。为不失一般性,首先考虑简化情况:1)两星之间由轻质杆连接;2)机械臂关节和抓捕部位在整个操控过程中锁紧,无相对运动;3)目标航天器无姿态机动能力。此时,组合体航天器可看作刚体,则用四元数描述的航天器姿态动力学为
然而,针对捕获非合作目标后形成的组合体,由于目标质量特性参数未知,其转动惯量c是难以精确已知的。另一方面,考虑到目标可能尚存姿态机动能力以及抓捕点处存在相对运动的情况,因而难以通过在轨辨识获得组合体航天器的精确数学模型。由于组合体航天器姿态模型中服务航天器的转动惯量已知,可将其作为先验模型用于控制算法的设计。



1.2 问题描述
本论文的控制目标为,针对模型部分未知以及目标航天器存在姿态机动情况下的系统动力学(4)。利用在轨运行输入输出数据建立非参数化数据驱动模型,并进一步提出基于数据驱动模型的组合体航天器姿态学习控制算法,使得系统状态稳定快速收敛到平衡点,实现对目标航天器的有效姿态接管。
2 组合体航天器GPR模型建立
2.1 GPR




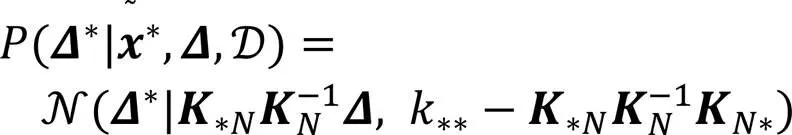

进一步地,通过极大化对数边缘似然函数:

2.2 基于变分推理的稀疏高斯过程回归
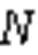

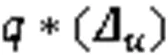
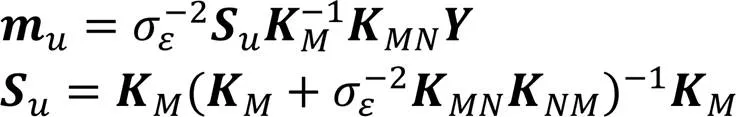
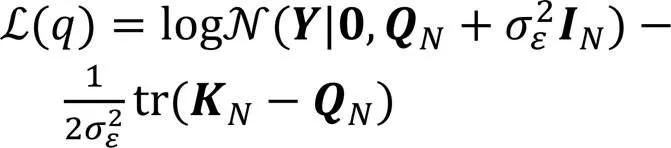

其均值矩阵和方差函数矩阵分别为
3 基于GPR的姿态接管控制

在进行控制算法设计之前,首先给出所需的引理和假设如下。



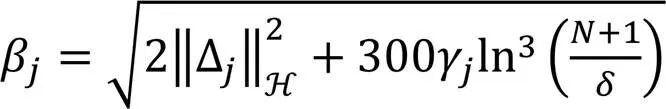
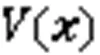
式中:k1、k2、k1、k2均为正常数。
则基于稀疏变分高斯过程的控制律可设计为
本节的主要结果在定理1中给出。

证 将控制律(28)代入动力学方程(3)中,得到闭环系统:
考虑Lyapunov候选函数为
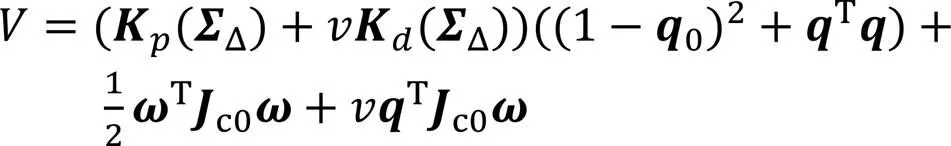
进而根据Cauchy-Schwartz不等式,可得:
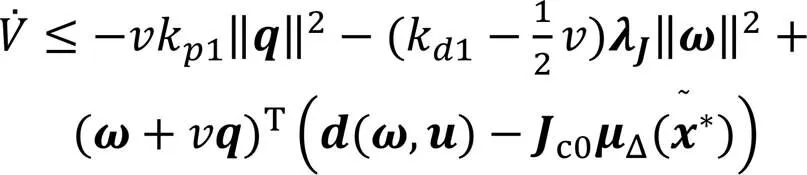
进一步结合引理2,有下式成立:

其中,

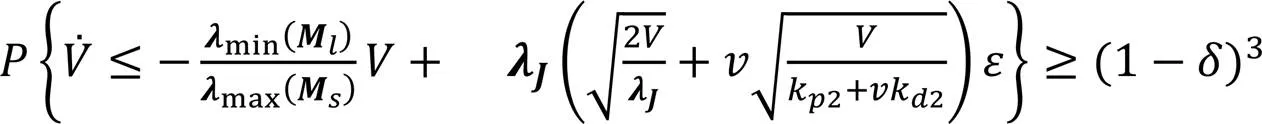


式中:sup(·)为函数的上确界。
进一步可得四元数矢量部分的上界为


4 仿真分析
4.1 GP模型的训练与验证


图2 PD控制律激励下GP模型响应曲线及95%置信区间

图3 PD控制律激励下GP模型回归误差绝对值
同时,标准GP和SVGP(粗体表示)在不同容量的数据集上的学习效果在训练时间和回归误差方面的量化对比见表1。由于训练阶段的计算量与数据集容量之间呈立方相关,随着数据集容量从500增加到2 000,标准GP训练所需时间从6.31 s显著增长到303.78 s,而稀疏GP模型的训练时间仅从1.56 s增加到3.64 s,但仍保持了与标准GP相当水平的均方误差。在实际应用中,数据集容量的大小是计算量与回归精度之间的权衡。
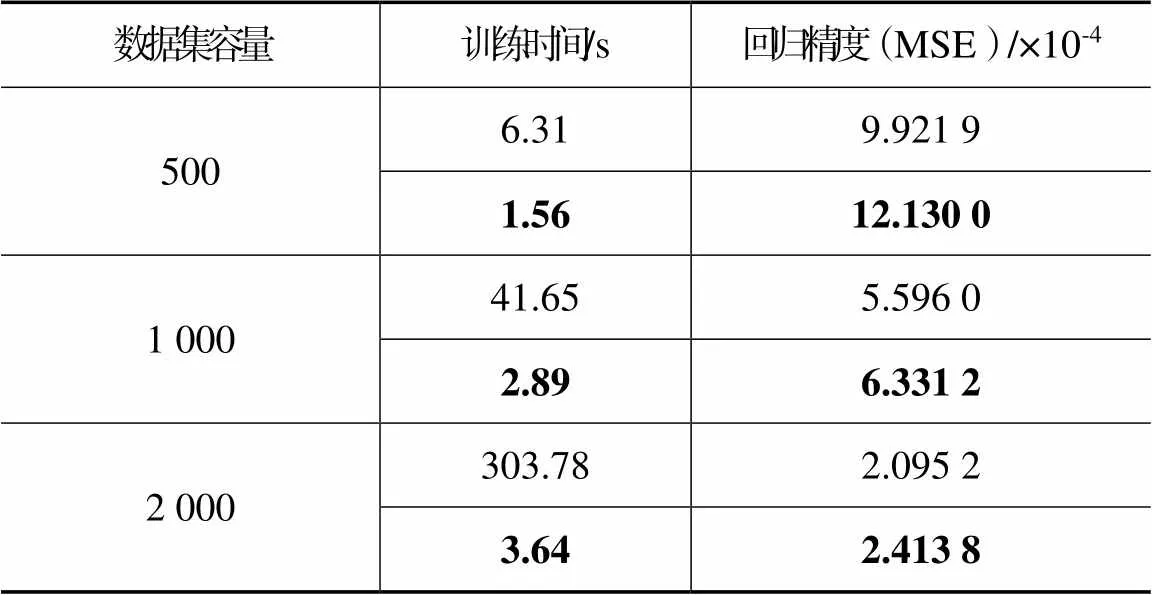
表1 GP训练时间、回归精度与数据集容量之间关系
4.2 存在未知模型不确定性时的仿真场景
本小节进一步给出所提出算法在线应用的仿真结果。假设目标航天器在整个姿态接管任务过程中始终进行主动姿态机动:当服务航天器对目标航天器施加姿态控制力矩使其偏离初始姿态指向时,目标航天器将对该力矩产生“对抗”控制力矩。此时,未知模型不确定性中包含2部分:1)除标称刚体模型外的未知姿态动力学;2)因目标航天器自身姿态指向偏移期望值,其产生的姿态对抗力矩对整个组合体航天器造成的附加姿态动力学。目标航天器的主动姿态控制律选为PD形式:



图5 服务航天器姿态角速度

图6 服务航天器姿态控制力矩
可以看到,在目标存在如式(42)所示PD控制形式的主动姿态机动力矩以及未知模型不确定性的作用下,2种控制算法均可实现姿态镇定的目标。从图4和图5可得,本文提出的基于稀疏GP的学习控制律无论是在动态响应还是稳态误差都较于基准控制律得到了明显的提升,最后可以使得状态收敛至更小的集合内。这主要取决于GP模型补偿机制的引入,因而目标姿态机动力矩和模型未知部分可以在控制律中被有效补偿。
姿态重机动后标准GP模型响应如图7所示。当组合体航天器姿态机动至训练集之外的区域时,GP的预测方差(由阴影填充的95%置信区间表示)显著增加,表示当前GP的预测均值与实际未知函数值之间具有较大误差,这也使得本文提出的基于GP的学习控制算法的反馈增益适当增大以进一步抵抗模型误差带来的负面影响。

图7 姿态重机动后标准GPR模型响应
5 结术语
本文研究了目标存在未知姿态机动特性的空间非合作目标捕获后的姿态接管控制问题。针对捕获后的姿态镇定问题,同时考虑到在轨任务的实时性、星载计算机的计算资源有限等因素,提出了一种基于稀疏GP的姿态接管学习控制策略,其反馈控制增益的大小可随GP模型的置信度而自适应地变化,并证明了系统状态可以实现概率意义上的最终一致有界收敛到平衡点附近的邻域内。相比于现有研究方法,本文所提出的控制策略可避免耗时的在轨模型精确辨识过程,同时对测量噪声、外界干扰、目标主动姿态机动具有较强的鲁棒性,可有效支撑在轨任务的高效处理。
[1] 杨自鹏,胡声超,周佑君,等.多任务在轨服务模块化智能航天器技术研究[J].宇航总体技术,2019,3(4):15-20.
[2] 龚自正,徐坤博,牟永强,等.空间碎片环境现状与主动移除技术[J].航天器环境工程,2014,31(2):129-135.
[3] 肖余之,靳永强,陈欢龙,等.在轨服务若干关键技术研究进展[J].上海航天(中英文),2021,38(3):85-95.
[4] LEBLOND P, LE BERRE F. ATV mission operations-system testing and operability with space network system[C]// Proceedings the 24th AIAA International Communications Satellite Systems Conference. Reston, USA: AIAA Press, 2006: 2006-5407.
[5] ODA M. Experiences and lessons learned from the ETS‑Ⅶ robot satellite[C]// Proceedings of the International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 2000: 914-919.
[6] LIU H, LI Z, LIU Y, et al. Key technologies of TianGong-2 robotic hand and its on-orbit experiments[J]. Scientia Sinica Technologica, 2018, 48(12):1313-1320.
[7] FLORES-ABAD A, CRAIN A, NANDAYAPA M, et al. Disturbance observer-based impedance control for a compliance capture of an object in space[C]// Proceedings of AIAA Guidance, Navigation, and Control Conference. Reston, USA: AIAA Press, 2018: 1329.
[8] HOVELL K, ULRICH S. Postcapture dynamics and experimental validation of subtethered space debris[J]. Journal of Guidance, Control, and Dynamics, 2017, 41(2):519-525.
[9] WANG Z, YUAN J, CHE D. Adaptive attitude takeover control for space non-cooperative targets with stochastic actuator faults[J]. Optik, 2017, 137: 279-290.
[10] ZHAO Q, DUAN G. Concurrent learning adaptive finite-time control for spacecraft with inertia parameter identification under external disturbance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(6): 3691-3704.
[11] GUO X, TIAN M, LI Q, et al. Multiple-fault diagnosis for spacecraft attitude control systems using RBFNN-based observers[J]. Aerospace Science and Technology, 2020, 106: 106195.
[12] CHEN B, WU C, JAN Y. Adaptive fuzzy mixed2/∞attitude control of spacecraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(4): 1343-1359.
[13] WILLIAMS C K, RASMUSSEN C E. Gaussian processes for regression[C]// NIPS. 1995: 2877073.
[14] BECKERS T, KULIĆ D, HIRCHE S. Stable gaussian process based tracking control of Euler-lagrange systems[J]. Automatica, 2019, 103: 390-397.
[15] LIU Y, TÓTH R. Learning based model predictive control for quadcopters with dual gaussian process[C]// 60th IEEE Conference on Decision and Control. Washington D.C., USA: IEEE Press, 2021: 1515-1522.
[16] PENG H, BAI X. Gaussian processes for improving orbit prediction accuracy[J]. Acta Astronautica, 2019, 161: 44-56.
[17] 庞梦非,朱春艳,张美艳,等.具有不确定性连接刚度的太阳电池阵基频分析[J].上海航天(中英文), 2017,34(6):103-108.
[18] MILLER K. On the inverse of the sum of matrices[J]. Mathematics Magazine, 1981, 54(2): 67-72.
[19] THEODORIDIS S. Machine learning: a Bayesian and optimization perspective[M]. London, United Kingdom:Academic Press, 2015.
[20] BLEI D M, KUCUKELBIR A, MCAULIFFE J D. Variational inference: a review for statisticians[J]. Journal of the American statistical Association, 2017, 112(518):859-877.
[21] STEINWART I, CHRISTMANN A. Support vector machines[M]. Berlin, Germany: Springer Science & Business Media, 2008.
[22] DEISENROTH M, RASMUSSEN C E. PILCO: a model-based and data-efficient approach to policy search[C]//Proceedings of the 28th International Conference on Machine Learning. New York, USA: ACM Press, 2011:465-472.
Gaussian Process Regression-Based Learning Control for Combined Spacecraft Attitude Takeover
MAGuangfu, LIUYuhan, LYUYueyong, GUOYanning
(Department of Control Science and Engineering, Harbin Institute of Technology, Harbin 150001, Heilongjiang, China)
Non-cooperative targets generally have the characteristics of complex structures, unknown inertia matrices, unknown attitude maneuverability, etc., which make the combined spacecraft attitude dynamics present highly nonlinear and strong coupling performances and hard to be accurately identified on orbit. In this paper, a sparse Gaussian process regression (GPR) based attitude takeover control strategy is proposed for the combined spacecraft after capturing a non-cooperative target with active maneuverability. Firstly, the costly on-orbit identification is avoided, while only the I/O data collected during the on-board operation is utilized to obtain a sparse GPR model to rapidly compensate the unknown dynamics. Then, a novel adaptive feedback gain control strategy is presented according to the learnt model, and the rigorous theoretical proof of all related closed-loop uniform ultimate bounded (UUB) stability guarantees is provided. It is shown that the proposed strategy can significantly reduce the on-board computational load while ensuring the control accuracy. Finally, numerical simulations are carried out to validate the effectiveness and practical value of the proposed strategy.
combined spacecraft; attitude takeover; non-cooperative target; Gaussian process; learning-based control
2022‑04‑29;
2022‑06‑17
国家自然科学基金(61973100,61876050,12150008);空间智能控制技术实验室开放基金课题(HTKJ2022KL502012)
马广富(1963—),男,博士,教授,主要研究方向为在轨服务、航天器姿态控制和智能控制。
吕跃勇(1983—),男,博士,副研究员,主要研究方向为在轨服务、航天器姿态控制和智能控制。
TP 273
A
10.19328/j.cnki.2096⁃8655.2022.04.004

