数据丢包下事件驱动的非线性多智能体迭代学习控制
王宏伟 李昊哲
(1.大连理工大学控制科学与工程学院,辽宁大连 116024;2.新疆大学电气工程学院,新疆乌鲁木齐 830047)
1 引言
多智能体系统是一类复杂系统,由多个具有独立感知、计算和通信能力的智能体组成[1–2],具备执行、解决大型复杂实际问题的能力,现已被广泛应用于诸多领域,如:卫星编队的姿态控制、无人机密集编队飞行控制、自主水下机器人导航和智慧工厂等[3–6].由于多智能体系统具备自主性、分布性、协调性和自主学习能力.目前,控制领域的专家学者对其进行了广泛研究,包括智能体的一致性[7–8]、网络通信存在延时的一致性问题[9–10]、智能体的集群[11–12]等.其中,一致性是实现其协同控制的首要任务.多智能体系统的一致性在广义上是指,网络中的所有智能体能实现状态演化或跟踪期望轨迹的一致.但是现有成果仅在时间域上研究多智能体的一致性,即随时间的推移系统的状态和输出趋于一致.但是,实际中存在一类具有重复运行特性的多智能体,能够在有限时间间隔内重复或周期性的执行特定任务.如,生产线上的多机械臂协同操作等.因此,这类问题就要求在有限时间区间内实现完全一致.
由于迭代学习控器的特点是结构简单,对模型信息要求低.因此,可以采用该方法对具有重复运行特性的多智能体系统进行控制.文献[13]首次使用迭代学习控制方法研究一类满足全局Lipschitz条件的非线性多智能体系统编队控制问题;文献[14]研究了在切换拓扑、初始状态转移和外部干扰情况下,一类不满足全局Lipschitz条件的非线性多智能体的鲁棒协作学习控制问题,随着迭代次数的增加,以指数形式快速收敛到期望的队形.文献[15]提出的迭代学习控制算法,解决了在领导者–跟随者网络通信框架下的非线性多智能体的一致性问题;文献[16]提出P型迭代学习控制方案,解决具有饱和约束的一类执行重复任务的非线性多智能体的控制问题.文献[17]采用迭代学习控制方法,研究了单积分情况下多智能体的一致性问题.文献[18]通过引入虚拟领导者技术,研究了系统参数时变情况下,离散线性多智能体在有限时间区间内的一致性问题,采用迭代学习控制方案,利用拓扑结构中的通信权值组合获得理想的控制率,实现对期望轨迹的完全跟踪.
上述文献所提出的迭代学习控制器,均需要智能体间的数据传输连续更新,会造成过高的能量消耗.另外,从网络资源利用的角度分析,若智能体系统运行在理想状态下,还周期性的接收和发送数据,会造成网路通信资源的不必要浪费.因此,事件触发的控制策略被广泛研究,并已取得较多优秀成果.文献[19]研究出一种具有事件触发机制的自适应输出反馈控制策略,解决受外部扰动情况下的线性多智能体的一致性.该触发机制的特点是不需要对测量误差实施连续监测.文献[20]提出基于事件触发机制的非线性控制策略,解决具有非线性特点的多智能体系统固定时间一致性问题.但是,从触发机制设计的角度分析,现有的事件触发机制不仅需要自身的状态数据,还需要邻居传输状态数据.如果网络数据传输出现丢包等问题,会影响上述触发机制的执行、进而影响控制效果.因此,该触发机制具有一定的局限性.同时,很少有文献讨论在迭代学习控制下,且模型信息未知的非线性多智能体系统的事件触发通信机制,这也是本文研究的重点.
另一方面,网络的稳定性和带宽的限制也给多智能体系统一致性控制带来新挑战.在数据传输过程中,通信链路故障经常发生,会造成数据随机丢包问题.许多文献为此进行了大量研究.文献[21–22]研究了同构多智能体系统在随机链路故障下的一致性问题.文献[23]针对服从伯努利分布的随机链路故障下的异构多智能体系统,利用邻居发送的前一步或两步状态信息设计故障控制协议.
分析上述文献发现,在多智能体迭代学习控制的现有成果中,文献[17–18]中研究的多智能体系统是线性且模型已知.然而,实际的系统往往是非线性的,并且很难获得精确的动力学模型.虽然在文献[13–16]中研究了非线性多智能体的一致性问题,但是这些结果要求系统的动力学是仿射函数,即控制输入项是线性已知的.然而,实际的多智能体系统却很难建立精确的数学模型,大多是模型未知的非线性系统.文献[24]首次提出了无模型自适应迭代学习控制方法,解决具有重复运行特性的模型未知的非线性多智能体系统的一致性轨迹跟踪问题.在此基础上,文献[25]将该方法成功应用到编队控制中.文献[26]研究出一种基于干扰补偿机制的无模型自适应迭代学习控制算法.虽然文献[24–26]提出了分布式无模型控制策略,但在数据传输方式上仍属于时间驱动的控制协议,即数据经过网络以分组的方式被周期性的发送和接收.由于实际通信过程中硬件设备的通信带宽是有限的,时间驱动控制方案可能会影响系统的一致性跟踪.另外,从网络资源利用的角度来看,时间驱动控制协议会造成不必要的通信资源浪费.同时,通信链路故障的影响也尚未得到处理.
在上述研究成果的基础上,本文提出一种事件驱动的分布式迭代学习控制策略,用以解决通信带宽受限,链路数据随机丢失且模型未知的非线性多智能体在有限时间区间内的一致性问题.通过对比现有的优秀成果,本文的主要贡献如下:1)本文使用智能体的输出数据沿迭代轴方向设计了一种全新的事件驱动通信机制,并给出事件触发条件,该条件无需邻居信息的参与.每个智能体可以决定当前的输出数据是否应该传输给邻居,有效的减少智能体间的冗余通信,降低系统的能量耗散,更好的节约带宽和通信资源;2) 设计故障补偿机制,该机制是基于伯努利概率序列,以及邻居智能体在前一步事件触发时刻的输出信息,能较好的应对链路数据丢包的随机性;3)在理论上使用压缩映射原理分析了所提控制策略的收敛性能,并给出使系统实现零误差一致性跟踪的充分条件;同时还在理论上证明了事件驱动通信机制的性质.当迭代次数趋于无穷时,各个智能体沿迭代轴方向的事件触发间隔也会趋于无穷,这意味着如果迭代次数足够大,任意两个相邻智能体间的通信触发频率都会有所降低.
本文内容安排如下:第2小节介绍研究的主要内容,包括智能体的动力学描述、图论定义和数据丢包描述;第3小节是控制方案,包括事件驱动通信机制设计,分布式控制协议设计;主要结果,即定理的给出和算法的收敛性分析将在第4小结给出;第5小节通过数值模拟验证所提方法的有效性;第6小节是总结和未来研究展望.
2 问题描述
考虑由1标记到q的q个异构非线性离散时间多智能体组成的多智能体系统,每个智能体具有在有限时间区间内重复运行的特性.其中第i个智能体的动力学描述如下:

其中:i=1,···,q;yi(k,l)和ui(k,l)分别代表智能体i的第l次迭代和第k个采样时刻的输出和输入数据;k∈[0,1,···,T],l=1,2,···;ny和nu表示两未知的正整数;fi(·)是未知的非仿射函数,因为各个智能体的fi(·)有不同结构,所以由q个智能体组成的多智能体系统是异构的.
系统(1)满足以下两个假设:
假设1在有限采样时刻内,fi(·)相对于控制输入ui(k,l)的偏导数是连续的.
假设2对于所有的采样时刻k ∈[0,1,···,T]和迭代次数l=1,2,···,若|ui(k,l)=0,则系统(1)满足沿迭代轴方向的广义Lipschitz条件,即
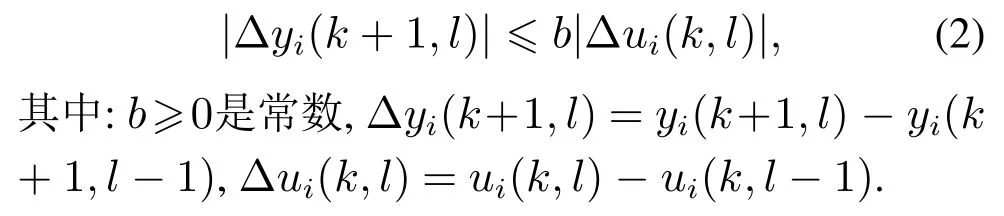
注1对于一般的非线性系统,上述两个假设存在的合理性已由文献[27]给出.因此,上述假设对于实际的非线性多智能体也是满足的.其中:假设1是控制器设计的一般约束条件,表示对于智能体i,若控制输入ui(k,l)在采样时刻k下沿迭代轴方向的变化所引起的系统输出yi(k+1,l)在采样时刻k+1的变化.假设2是对这种变化率上界的限制,表示与智能体i沿着迭代轴方向的控制输入变化率∆ui(k,l)相对应的输出变化率∆yi(k+1,l)是有界的.


当多智能体系统中的所有智能体满足假设1和假设2时,非线性系统(1)可以采用动态线性化方法得到等价的数据驱动模型.这方法仅使用在线的输入和输出数据,因此可得到如下引理.
引理1[24]当多智能体系统(1)满足假设1和假设2的情况下,若|ui(k,l)=0,则系统(1)可以转化为迭代轴上的紧格式(CFDL)数据驱动模型

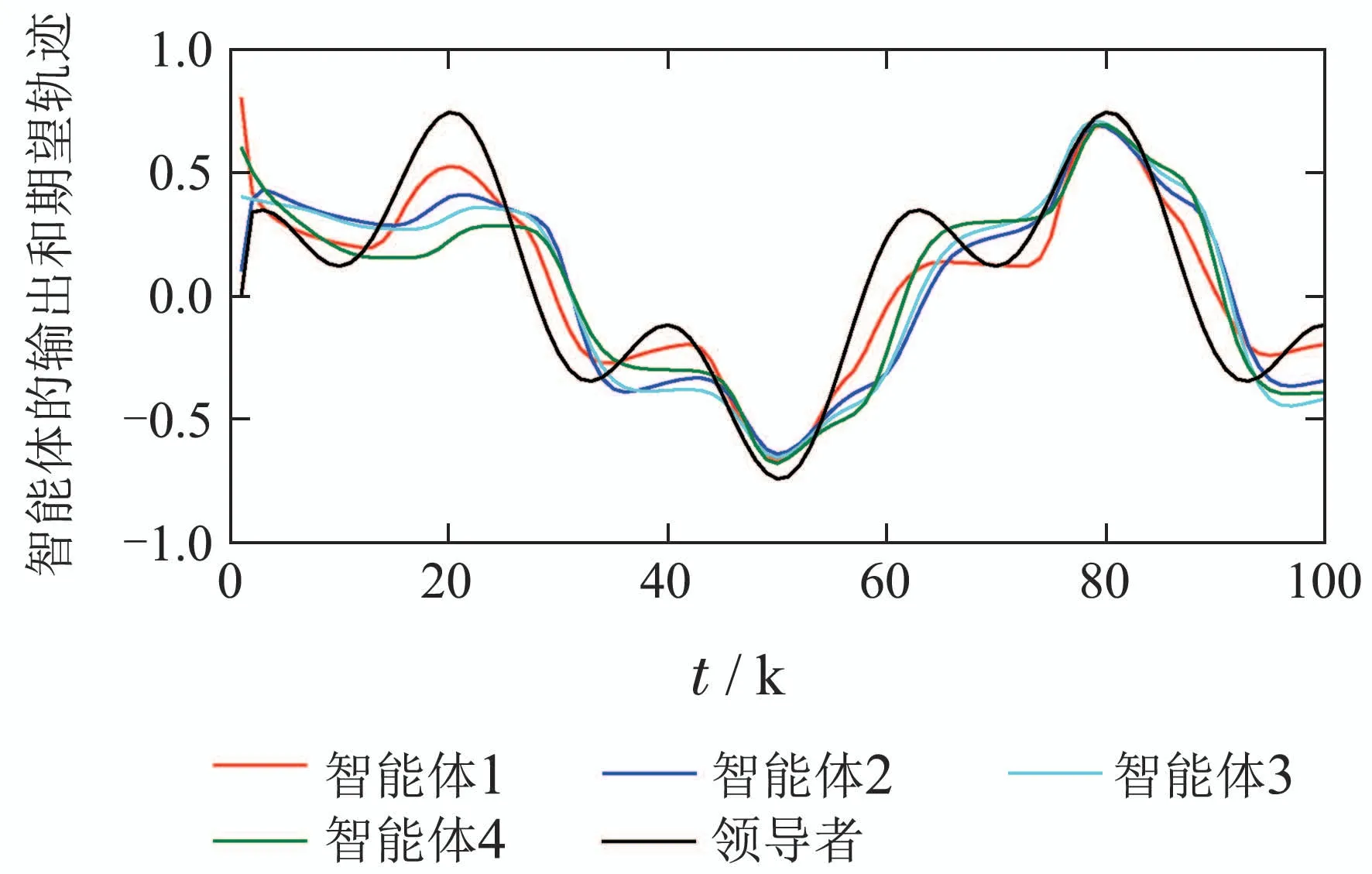
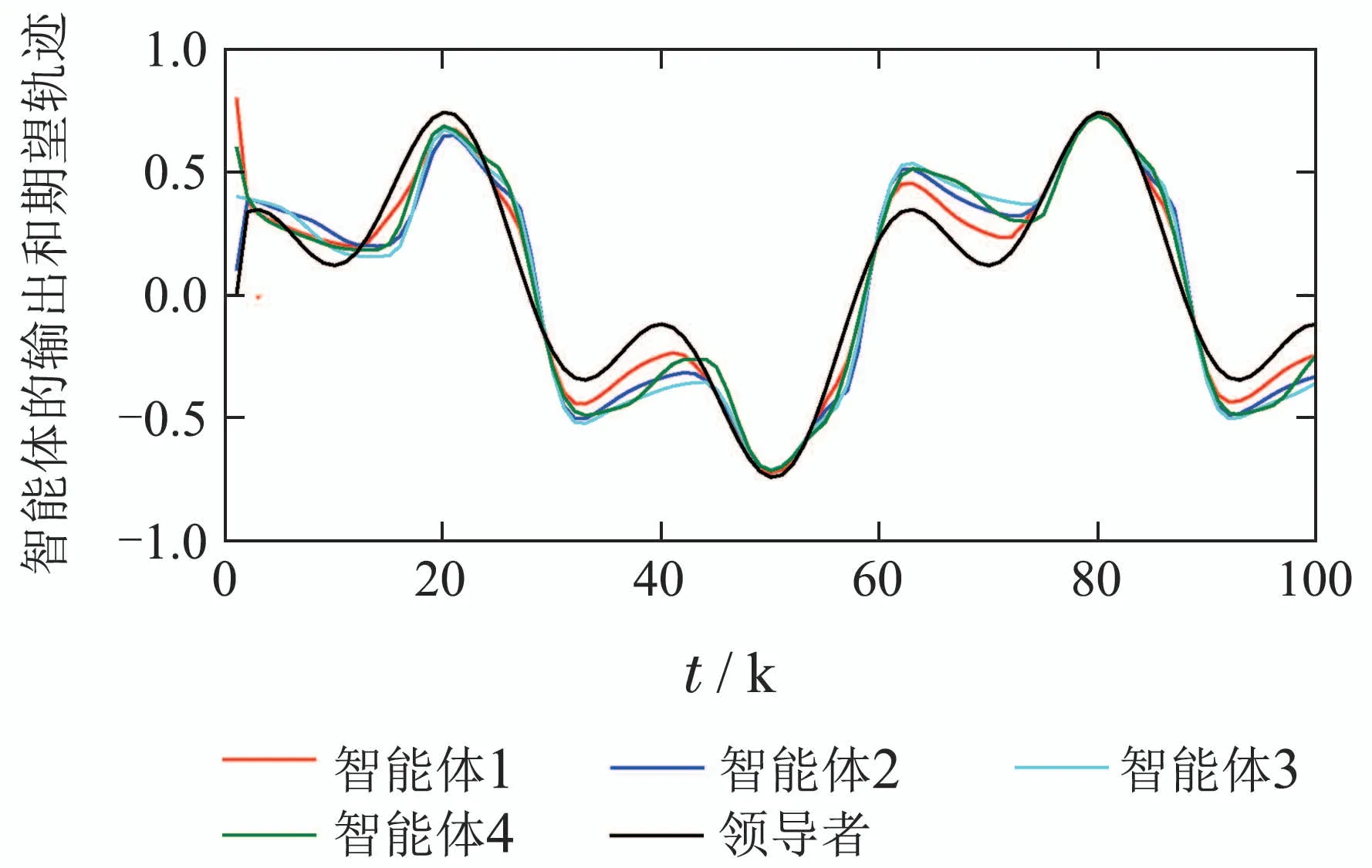
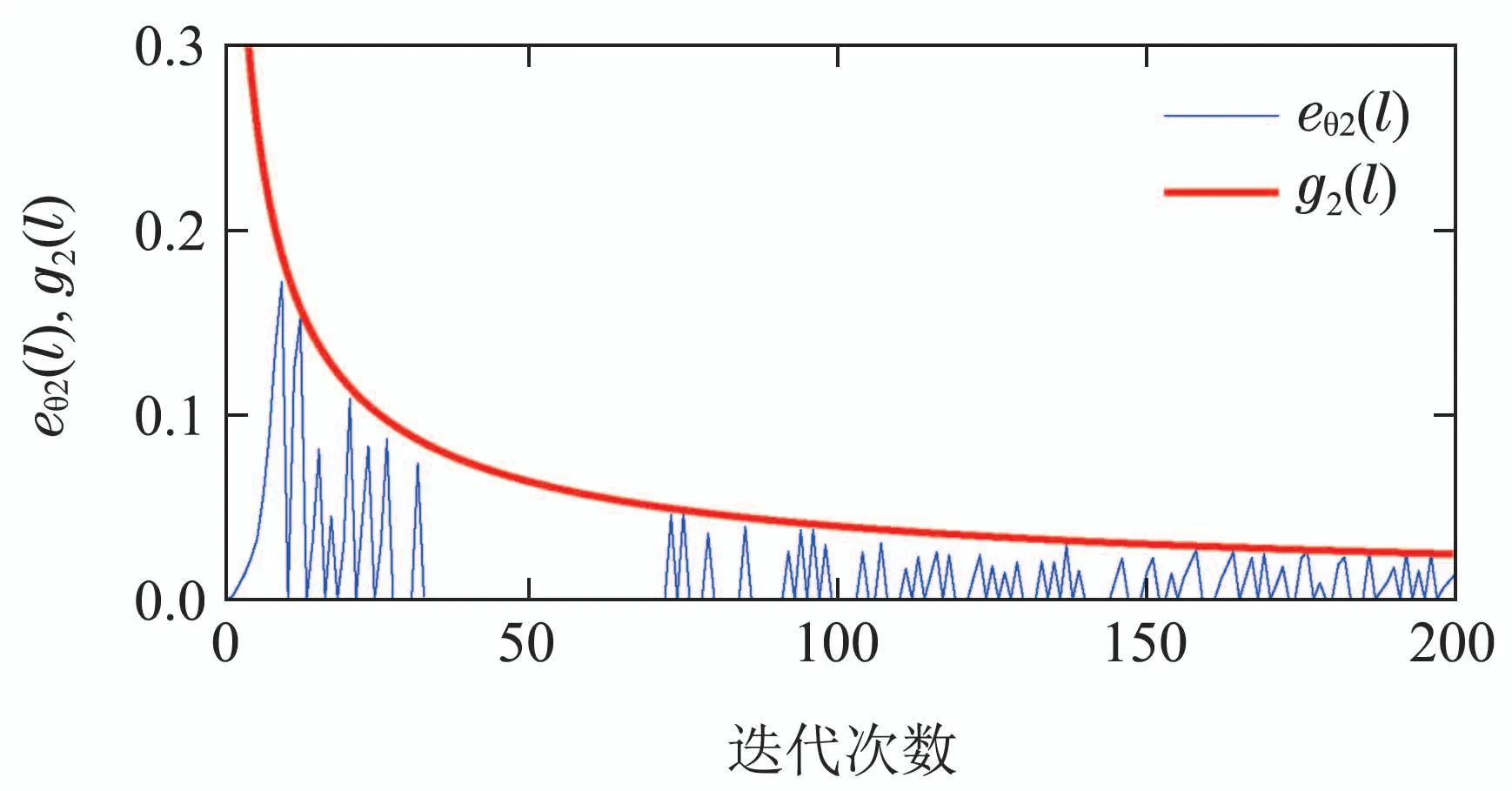
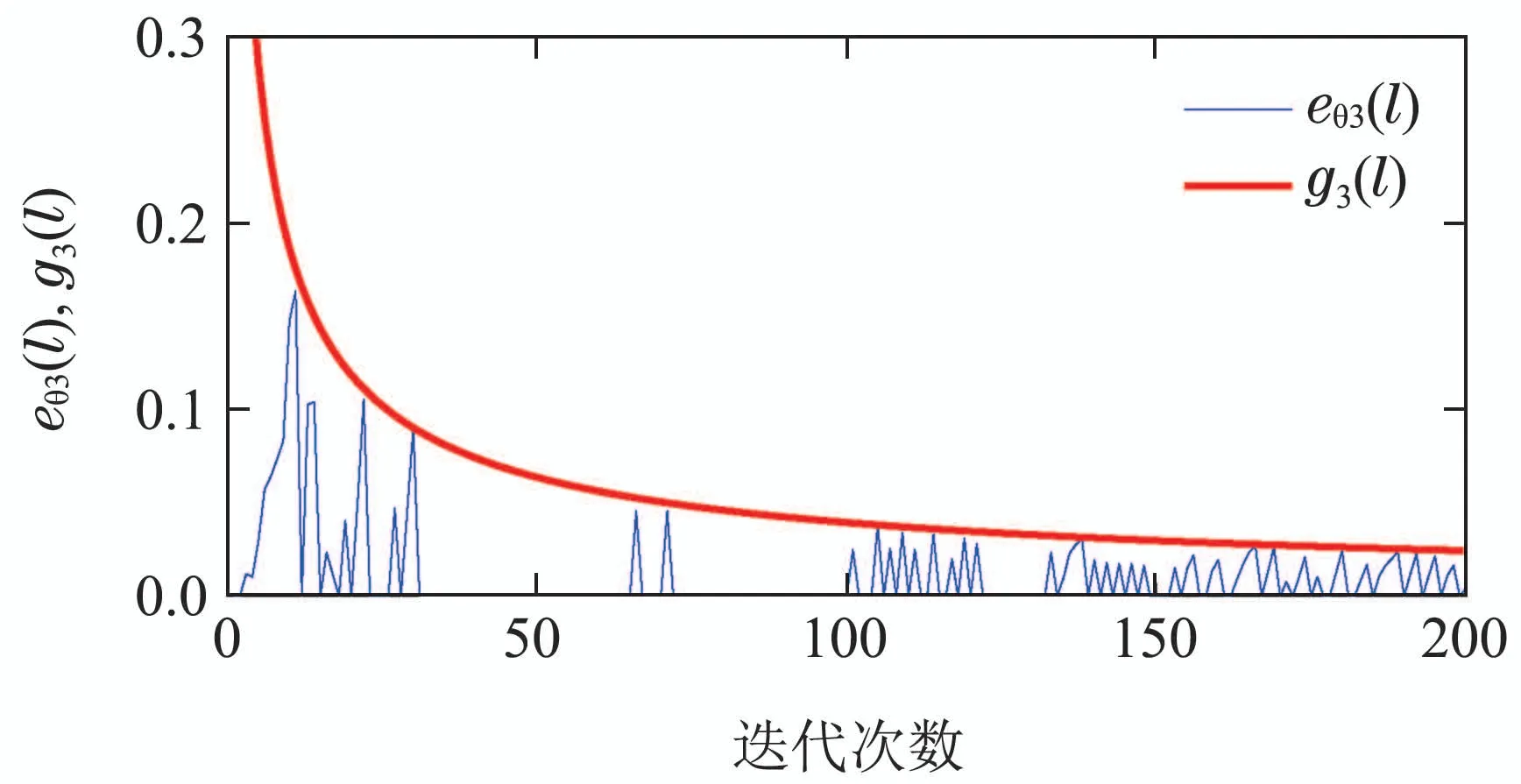
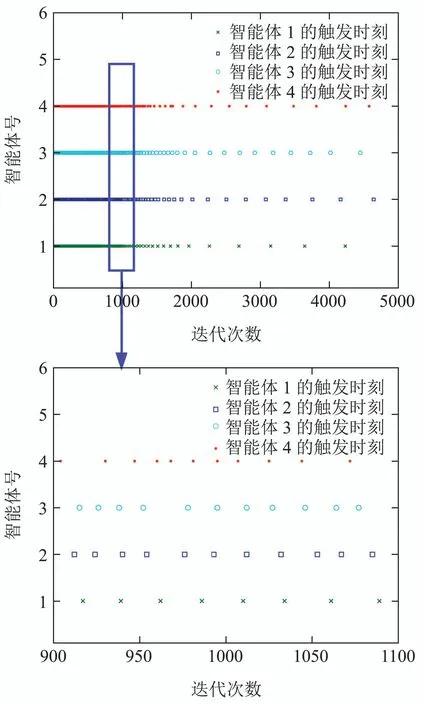
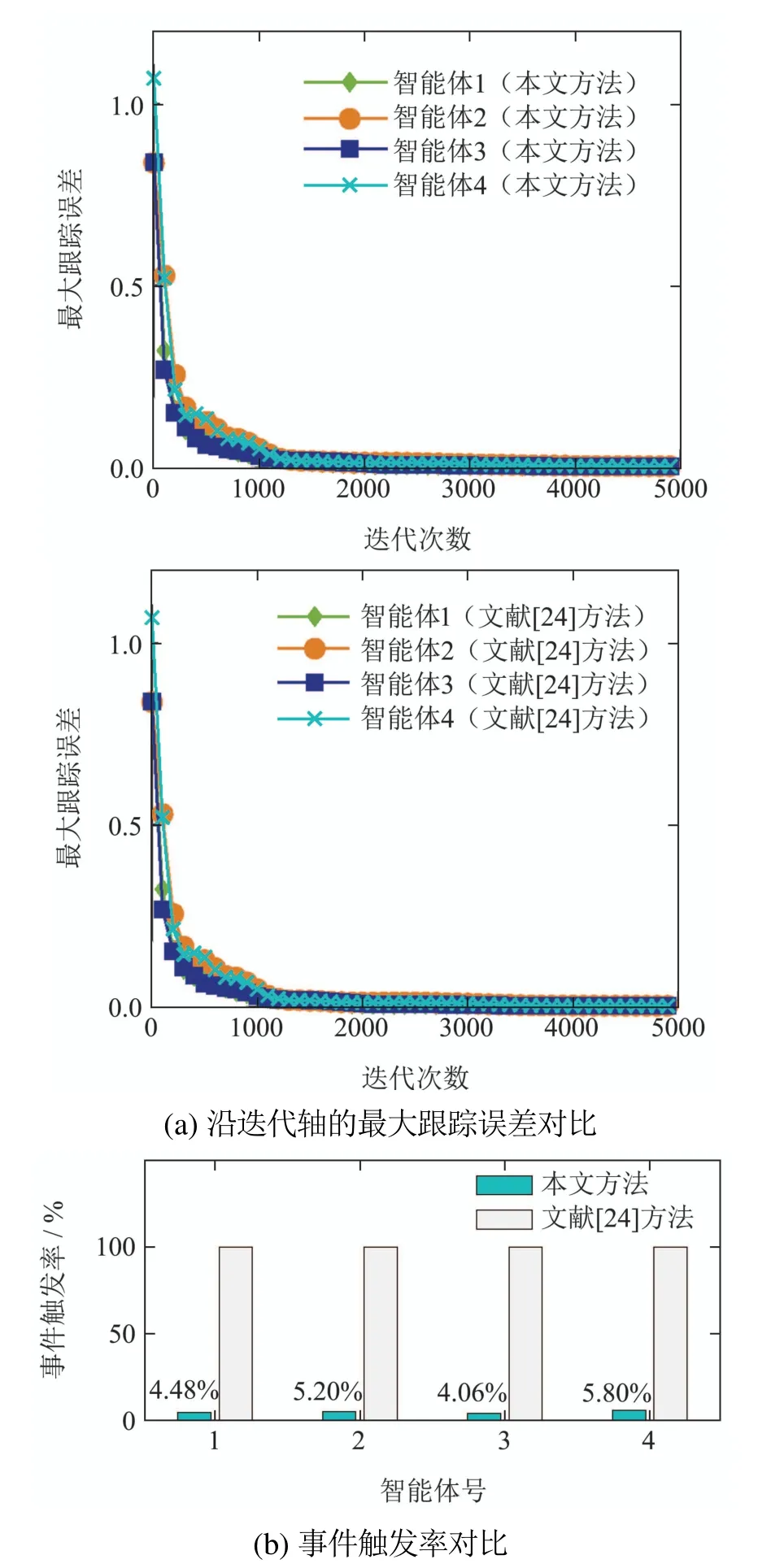
其中:φi(k,l)是一个与迭代次数l相关的PPD时变参数,并且对于任意的采样时刻k和迭代次数l,φi(k,l)是有界的,满足|φi(k,l)| 注2数据驱动模型(3)是每个非线性智能体系统(1)的等效动态表示. 由于通信条件的限制,实际的网络节点之间通信链路故障经常发生,使得数据在传输过程中出现丢包问题.本文的随机链路丢包现象用αij(k,l)表示,其满足伯努利二项分布.αij(k,l)=0表示数据被成功传输,αij(k,l)=1 表示数据发生丢失. 其中0 ≤α≤1为已知参数. 注3αij(k,l)=1的下标ij仅表示节点vi到节点vj的通信链路出现故障.若节点vj到节点vi的通信链路发生故障,则αji(k,l)=1. 本文考虑期望轨迹yr(k)是由引入的虚拟领导者产生,yr(k)只被部分智能体访问.令虚拟领导者在拓扑中的顶点为v0,则可得到一个由q+1智能体组成的有向图其中:是边集;是图的加权邻接矩阵. 假设3期望轨迹yr(k)是有界的. 假设4有向通信拓扑图Gs ∈是强连通的,并且存在一个或多个智能体可以直接从虚拟领导者中获得期望轨迹信息. 定义跟踪误差为:ei(k,l)=yr(k)−yi(k,l),对多智能体系统(1)设计控制协议,能够使得所有智能体在迭代次数趋于无穷时,其跟踪误差ei(k,l)能够收敛于零. 在迭代过程中,让表示智能体i的最新事件触发时刻,则智能体i的触发事件定义如下: 其中:当智能体i满足事件触发条件时ςi(k,l)=0,否则ςi(k,l)=1. 注4该机制是自触发的事件驱动机制,仅仅使用智能体i的当前输出数据yi(k,l)和上一个事件触发时刻的输出数据yi()设计触发机制,无需邻居智能体的数据信息. 考虑带有随机链路丢包现象式(4)的数据传输过程,根据事件驱动通信机制(5)–(11),设计如下的无模型自适应迭代学习控制算法: 注5PPD参数估计算法(12)和控制算法(14)都是递归形式,仅使用实时的I/O数据和先前时刻的相关参数进行更新.因此,该控制协议是数据驱动的. 为便于收敛性的分析,给出如下的引理: 引理2[28]当且仅当拓扑图Gs的邻接矩阵是不可约的,拓扑图Gs是强连通的. 引理3[29]令W(t)是一个时变的主对角线元素为正的不可约的亚随机矩阵.其中:W ⊂RN×N表示所有可能的W(t)组成的集.使得, 其中:0<λ<1,且W(t),t=1,2,···,p.p个矩阵是从集合W中任意选取. 针对非线性多智能体系统(1)设计的分布式控制协议,可得如下定理: 证本节分为a)–c)3个部分去证明所提方法的收敛性. a)事件驱动通信机制的性质. 根据引理1,得到φi(k,l)有界于常数b,再由假设2可知|φi(k,l)|≤b,所以容易得出|∆φi(k,l)|≤2b.下面对式(25)两端取绝对值,可以得到 特别指出,对于常数d只需证明其存在的合理性,而无需讨论其具体数值. 将式(27)代入至式(26)中得 下面分别给出分布式跟踪误差(29),控制律(14)和数据驱动模型(3)的紧凑形式. 分布式跟踪误差(29)的紧凑形式如下: 又因为通信拓扑满足强连通,根据引理1的结论,则矩阵I −ρr(k,l)一定是不可约矩阵. 若式(35)成立的前提下,当控制器参数ρ满足如下条件时: 则方阵I −ρr(k,l)一定是主对角线元素为正且不可约的亚随机矩阵,方阵I −ρr(k,l)中至少有一行元素之和严格小于1. 对于式(34),当∀k ∈[0,1,···,T],可得到如下的递推不等式: 根据式(37),为进一步分析收敛性,需证明下面集合中的每个元素都是有界的: 由于B(k,n)=[bij(k,n)],bij(k,n)的值是由网络拓扑结构、丢包因子和激活函数三者共同决定的.这样bij(k,n)的值可能是0,1或2.因此一定会存在一个常数θkn >0,使得∥B(k,n)∥<θkn.取 本节通过一个离散时间非线性多智能体系统来验证所提方案的有效性.值得注意的是,分布式控制协议中没有使用系统的任何模型信息,包括系统的阶数,线性和非线性特征.仿真所给出的数值模型仅为产生相应的I/O数据,并末参与控制协议的设计. 考虑系统是由一个虚拟领导者和4个智能体组成,对智能体依次标号为1至4,通信拓扑结构如图1所示.第i个智能体的非线性结构如下: 图1 3个强连通的通信拓扑Fig.1 Three strongly connected communication topologies 图1描绘了所有可能出现的通信拓扑结构,有向图集合表示为¯G={G1,G2,G3},并且在每个拓扑图中虚拟领导者用0表示.仿真中引入标签函数σl ∈n={1,2,3}在每次迭代时随机选择有向图集合中的元素,构成切换通信拓扑,切换规律如图2所示.相应的每个拓扑图所对应的Laplacian矩阵为 图2 拓扑结构切换规律Fig.2 The rule of topology switching 并且,H1=diag{1,0,0,1},H2=diag{1,1,0,0}以及H3=diag{1,0,0,1}.将控制协议(12)–(16)应用于系统(41).其中:系统重复运行的采样时间k ∈{0,1,···,100}.随机变量αij(k,l)服从伯努利分布,满足 对于所有的智能体i=1,2,3,4,θ(k)=(1+round(k/50)),初始状态yi(0,1)是区间为[−0.1,0.1]的随机数.受控系统控制信号的初始条件为ui(0,1)=0.伪偏导数(PPD)的初值设置为(k,1)=0.1.其它的控制协议参数设置为η=0.6,µ=1,ϖ=0.9,ε=0.05.此外,ρ=0.3<(1/3),τi=0.7,满足定理1的收敛条件. 由图3–图5可以看出所有智能体都能在迭代过程中实现有限时间区间内的轨迹跟踪.为更直观的表示出系统随迭代轴方向的跟踪误差变化,取出各个智能体在每次迭代过程中的最大跟踪误差作图6,以说明该方法在迭代域中的有效性.图7–图8分别表示智能体2和3在事件驱动控制协议(12)–(16)下,其事件驱动误差与阈值函数的演化过程. 图3 第100次迭代时的各智能体的输出yi(k+1,l)曲线与期望轨迹Fig.3 Output yi(k +1,l) of agents at the 100th and desired trajectory curve 图4 第200次迭代时的各个智能体的输出yi(k+1,l)曲线与期望轨迹Fig.4 Output yi(k+1,l)of agents at the 200th and desired trajectory curve 图5 第1000次迭代时的各个智能体的输出yi(k+1,l)曲线与期望轨迹Fig.5 Output yi(k+1,l)of agents at the 1000th and desired trajectory curve 图6 各智能体沿迭代轴的最大跟踪误差Fig.6 Maximum tracking error of agents along the iterative axis 图7 智能体2的事件驱动误差及阈值变化趋势Fig.7 The evolution of event triggered error and threshold of agent2 图8 智能体3的事件驱动误差及阈值变化趋势Fig.8 The evolution of event triggered error and threshold of agent3 图9给出各个智能体的事件触发间隔,可以明显看出,各个智能体任意两个相邻事件触发间隔随迭代过程的增加而变大,这符合本文设计的事件驱动通信机制(5)–(11)的性质.表明所提出的事件驱动控制协议在减少系统能耗方面,节约通信带宽资源方面的优越性能. 图9 各智能体的触发间隔Fig.9 The triggered interval of each agent 定义事件触发率反映不同智能体在迭代轴方向的通信请求次数,ci=(zi/N)×100%,其中:zi表示智能体i在迭代过程中的事件触发通信次数,N表示系统的迭代次数.不同智能体的事件触发率情况如表1所示. 表1 各个智能体事件触发率统计结果Table 1 Statistical results of triggering rate of each agent 从上面的仿真中可以得到,即使通信链路出现数据丢包,且通信网络随机切换,各个智能体在事件驱动的控制协议作用下,在有限的时间区间内随着迭代过程的增加,所有智能体的跟踪误差将收敛于零. 此外,为衡量事件触发通信机制对控制效果的影响,在不考虑数据丢包的情况下,与文献[24]中的DMFAILC算法进行了对比实验,实验结果如图10所示.根据图10(a)中最大跟踪误差曲线趋势可以发现,本文方法与文献[24]方法的控制效果基本类似.但是,从图10(b)中事件触发率的对比明显看出,本文方法的事件触发率低,在节约通信带宽资源和降低系统能量耗散方面,更优于采用时间驱动机制的DMFAILC算法,同时DMFAILC算法并末考虑数据丢包的问题.因此,本文所提出的控制协议,不仅具有更好的鲁棒性,而且还能有效降低智能体间的冗余通信,更好的节约带宽和通信资源. 图10 不同控制方法下性能指标对比Fig.10 Comparison of performance indexes in different control methods 本文研究了在有向切换拓扑下,随机链路故障、通信带宽受限以及模型末知的一组具有可重复运行特点的非线性多智能体的一致性问题,提出一种事件驱动的分布式无模型迭代学习控制策略.从网络资源利用的角度出发,考虑实际通信过程中的带宽限制和随机链路故障,提出了一种新的事件驱动通信机制和随机链路丢包补偿机制,能有效降低系统在通信过程中的能量耗散,且能够较好的应对链路数据丢包的随机性.然后,通过压缩映射的方法给出系统收敛的充分条件.该控制协议仅依靠自身的输入和输出数据以及邻居智能体的输出数据,无需被控对象的先验模型信息,计算效率高,便于工程实现. 在末来的工作中,结合现有的研究成果,将该方法推广至多输入多输出的非线性多智能体的一致性控制中.同时,对于拓扑结构随采样时间切换、系统外部噪声干扰和数据传输延时等情况依然值得深入研究.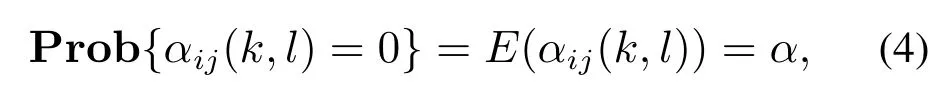
3 控制方案
3.1 事件驱动通信机制设计

3.2 分布式控制协议设计
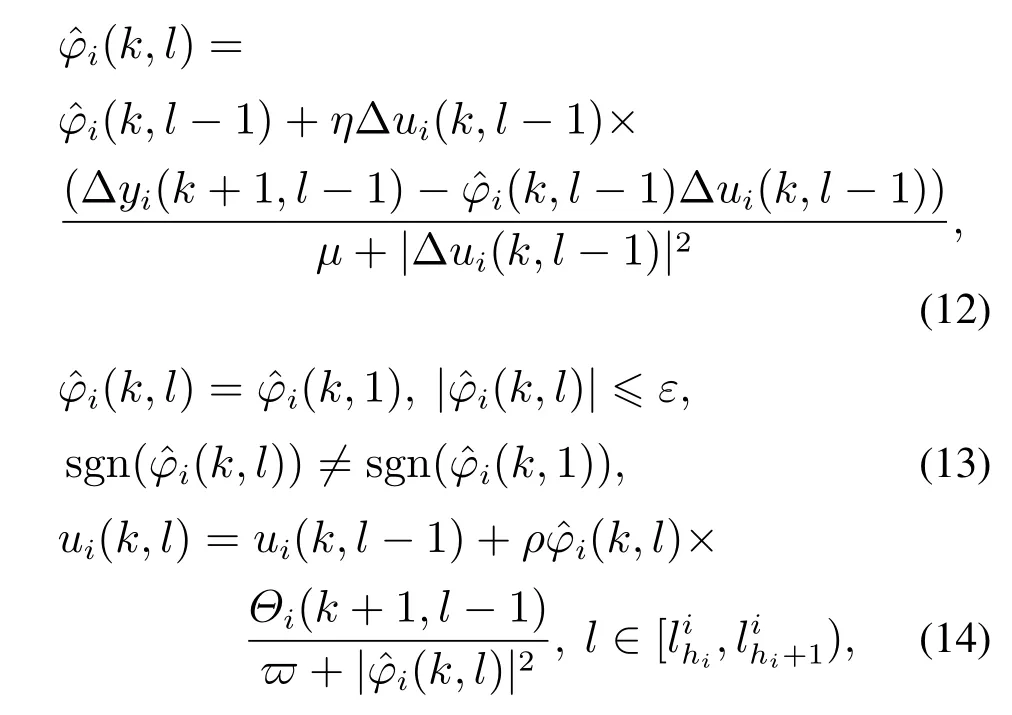

4 主要结果





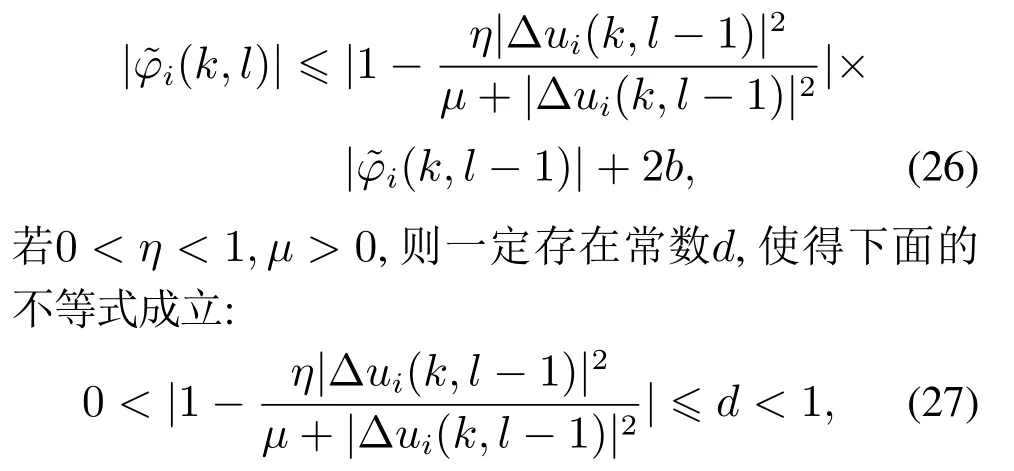






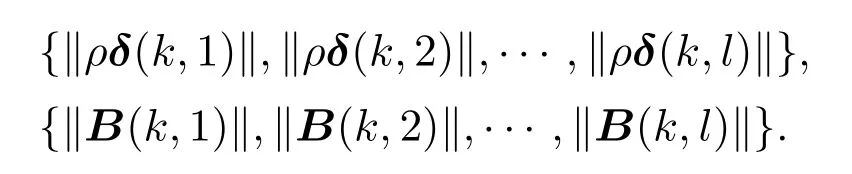


5 仿真示例
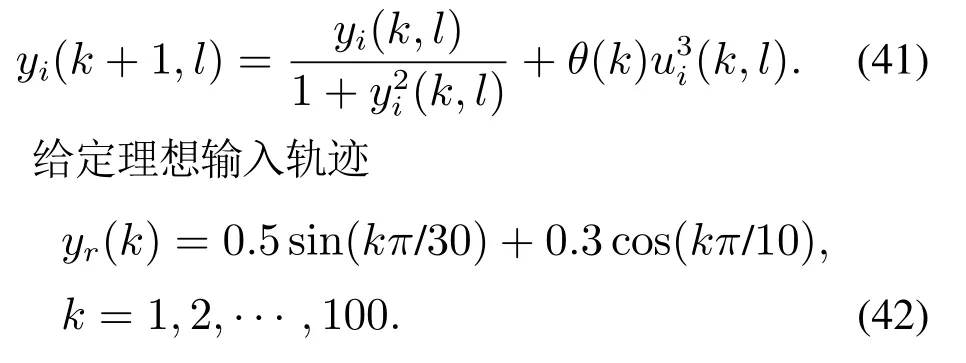



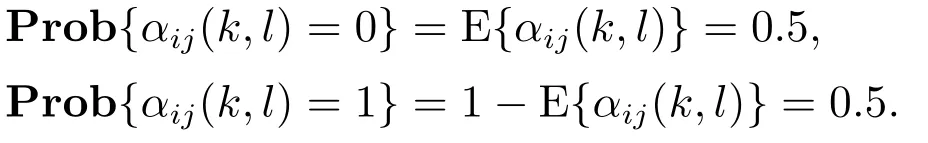



6 总结

