基于Peano分形的亚波长尺度声学超材料

吴光华, 柯艺波, 张 林, 陶 猛

(贵州大学 机械工程学院， 贵阳 550025)

声学超材料是一类周期性排列，可以对振动波的散射特性进行操控的人工结构，展现出自然材料中未发现的、独特的声学特性，为亚波长尺度上的声调控提供了可行性[1]。人工设计的超材料具有特殊的声学性能，原因在于其特殊的结构而不是材料成分，展现出广泛的应用前景，如声聚焦[2-4]、声学隐身[5]等。声波的调控基于布拉格散射机理和局域共振机理，前者在低频范围内产生带隙时，需要很大的结构尺寸[6]，后者是由亚波长尺度的共振单元引起的，可以不受空间尺寸的限制，产生低于传统的布拉格散射带隙的频带[7]。基于局域共振机理的人工声学超材料，可以在低频范围内进行声波调控，因而成为人们关注的焦点。

Liu等[8]将硅胶包覆在铅球外构成结构单元，并嵌入基体材料中，在结构共振频率附近，第一次实现了负质量密度的响应。Fang等[9]将亥母霍兹共振腔周期性排列，实现了负体积模量的响应，并通过改变共振腔腔体尺寸来调控带隙的频段。Yang等[10]采用薄膜结构，设计出可以实现负质量密度的声学超材料。Lee等[11]在前人的基础上，将薄膜型结构和亥母霍兹共振腔结合起来，实现了质量密度和体积模量同时为负值的超构材料。结构在特定频带内的带隙与声学超材料的负参数有关，单极共振时引起负的体积模量，偶极共振引起负的质量密度，当这两个参数任意一个为负数时，声的相速度为纯虚数，声波无法在介质内传播形成带隙[12]。Cheng等[13]基于Mie共振设计出一个具有8个声通道的圆形对称空间卷曲结构，研究了在单极和偶极共振时，结构中心区域产生能量聚集，实现了负等效质量密度和体积模量并设计出三维结构，为设计新型声学器件提供了新的途径。张嵩阳等[14]基于局域共振原理，设计了一种轻量的声学超材料板，并从试验测试的角度证明了设计的超材料板具有良好的低频宽带隔声性能。

基于结构共振机理设计的声学超材料会导致能量的高损耗，同时还有一些缺点，如结构不稳定，使用寿命短以及产生的带隙窄等。基于有效介质理论设计的空间卷曲超材料，结构简单，具有高对称性，可以产生负的色散关系，实现负折射。卷曲空间作为一种可以实现声学反常参数的方法，为超材料的设计提供了一种简单、可靠的方法[15-16]。Liang等首先提出一种对称性迷宫型超材料，通过延长声波在结构中的传播路径，实现了负折射率和密度接近零时的声隧穿现象。Liu等设计了一个螺旋形迷宫超材料，实现了声波在弯曲管道内的均匀传输。Xia等[17]设计出的亚波长尺度超结构，在低频下可以进行滤波和声隐身。

分形曲线作为一种空间填充曲线，因其曲线排列的规律性和自相似性，受到了广泛的关注[18-21]。本文基于Peano曲线，构建出一个对称的、具有亚波长内部通道的声学超材料，使声波沿着声通道传播，延长了声波路径长度，相位发生延迟。当结构尺寸有限时，能够通过改变结构中声通道的宽度来调控带隙和负群速度模式到所需的频率范围内。通过周期性排列结构单元进行仿真分析，观察到设计出的超材料具有波前整形、声隐身以及声隧穿等效应，为构建在低频下具有双负声学特性的声学超材料提供了一种新的思路。

1 分形结构的设计

1.1 分形曲线

图1表示Peano分形曲线的一阶、二阶形式。如图1(a)所示，正方形区域被划分为3×3个单元，从第一个单元的中心出发，按1-3-4-6-7-9顺序连接各个单元的中心，构成一阶Peano分形曲线。如图1(b)所示，将正方形区域划分为9个区域，每一个区域都由一阶分形曲线填充，按照同样的连接方式的将各个小区域按照顺序连接，构成了二阶分形曲线。二阶分形曲线是一阶分形曲线迭代延伸的结果，具有规律性和自相似性。

1.2 分形结构

如图2所示，基于上述Peano曲线设计出了分形结构，通过卷曲空间和增加分形阶数的方法，延长声波的传播路径，使得结构中的等效声传播速度低于在背景场中的速度，相当于构成了具有超低声速的人工介质。为确保结构对于来自于各个方向的声波都可以起到调控的作用，排列后可应用于更加广泛的场景，将其设计成对称结构。

(a) 一阶

选择环氧树脂作为构建分形结构的基体材料，其密度ρ1=1 050 kg/m3，声速c1=2 500 m/s；空气密度ρ0=1.29 kg/m3，声速c0=343 m/s。单元的晶格常数d=100 mm，基体材料边长a=94 mm。一阶Peano分形结构的内部声通道宽度w1=8 mm，二阶分形结构的内部声通道宽度w2=2 mm。

2 带隙特性与模态分析

量化分析与评价声学超材料中声波传输特性时，常用的表征参数包括带隙特性、模态分析、传输特性、态密度、等频率曲线、波长分布等。在本文中主要从其中主要的几个表征量:带隙特性、模态分布进行分析。

2.1 带隙特性

如图3(a)所示，在正方形点阵中均匀分布分形结构，其中正方形点阵的基向量为e=(e1,e2)，晶格点r的响应为u(r)。因为正方形点阵具有周期性，响应u(r)的周期性表达式为

u(r)=u(r+R)

(1)

式中，R是点阵的晶格矢量。

(a) 正方形点阵

位移响应u(r)利用傅里叶级数展开表示

(2)

将式(2)代入(1)式可得

Gj·R=2πk

(3)

式中,Gj是晶格的倒易点阵，其基向量表示为:

(4)

根据Bloch定理，响应向量u(r)可表达为

u(r)=eik·ruk(r)

(5)

式中：k=(kx,ky)是布里渊区的约束矢量；uk(rr)是点阵中的周期响应矢量。采用有限元法对分形结构的带隙进行分析，通过在单元周期性边界上设置Bloch-Floquet条件，从而计算获得结构的能带特性。

图4是两种分形结构的带隙分布图。从图4(a)中可以看出，在[0,1 600]Hz的频率范围内，一阶分形结构存在2条完全禁声带，分别是[580.4,750.4]和[1 008.4,1 158.2]Hz，在这些范围内，不存在任何弹性波的本征模式，声波或振动无法进行传播，实现了对弹性波能量传播的控制，带隙占比为20.3%。如图4(b)所示，在[0,1 600]Hz范围内，二阶分形结构存在6条带隙，分别是[210.1,327.6]、[408.8,423.0]、[630.2,695.4]、[813.4,845.8]、[1 209.8,1 276.8]和[1 559.9,1 600.0] Hz，带隙区域之外的声波都可以进行传播，带隙占比为21.6%。

(a) 一阶分形结构

在波长大于结构单元尺度的频段内，本文设计的亚波长结构单元产生了弹性波带隙，具有质量小、尺寸小但控制的波长大的特点，有助于突破传统降噪减振技术的局限。比较图4(a)和4(b)中的带隙分布特点不难看出：随着阶数的增加，带隙出现在更低的频段中。这是因为二阶分形结构的声通道的卷曲程度增加，声波的传播的距离增加。从这个角度出发，可以通过增加分形曲线的阶数，来设计出亚波长尺度的滤波器。

需要说明的是，分形结构的两个关键参数，声通道宽度和中心区域的面积，是考虑到结构体的鲁棒性而取的两个初始值，在合理的范围内可进行调整，当需要应用于不同的隔声降噪场合时，可以通过调整和优化结构的参数，来调整禁带的区域从而满足不同的需求。

2.2 模态分析

本征模态的计算是在有限元软件特征频率模块下，基于建立的Peano分形结构模型来进行的，结果用于理解禁声带隙的产生机理。如图5(a)所示，一阶分形结构的单极共振频率为987.9 Hz，其中心区域产生单一振动模式，并且均匀地向外扩展；如图5(c)所示，偶极共振频率为745.9 Hz，其结构左右两侧区域产生了相位完全相反的振动。一阶分形结构的单极和偶极共振产生的带隙分别为[1 008.4,1 158.2]和[580.4,750.4]Hz。图5(b)和(d)分别表示的是，二阶分形结构单极共振频率为328.4 Hz，偶极共振频率为388.9 Hz，其振动规律与一阶分形结构相同，单极和偶极共振产生的带隙分别为[210.1,327.6]和[408.8,423.0] Hz。不同于由局域共振单元产生的带隙，分形结构单极共振和偶极共振产生带隙时，其自身结构并不随着振动而变化。

3 等效密度

由声速与体积模量和质量密度关系式

(6)

式中:c是声速；ρ是质量密度；B是体积模量。

可以得出，介质的质量密度和体积模量中，任意一个声学参数为负值时，声的相速度为纯虚数，其中的声波以指数形式衰减，不能在介质中传播[12]。因此，分形结构产生带隙的原因在于材料的负等效声学参数，其单负声学参数处的频带对应的是声传播禁带。以下通过计算分形结构的声学特性曲线来验证带隙分布。

(a) 987.9 Hz

本文提出的分形结构质量分布不均，没有计算其动态质量密度和体积模量的固定算式，但作为一种亚波长结构，工作频段的弹性波在其中传播时，波长大于特征尺寸，从宏观角度来看，结构的声学特性近似于均匀介质，因此，可基于等效的理念，用均一化材料参数来描述其声学响应。

3.1 S参数提取法

研究周期性结构的声学特性的方法有以下几种：S参数提取法、变分法、平面波扩张法和传递矩阵法等。S参数提取法是在长波长尺寸的条件下，将材料结构视作一块各向同性的均匀等效介质板，通过提取等效介质板的反射系数(R)和透射系数(T)来计算材料的等效参数[22]。

如图6所示，在有限元模型中，介质两边设置周期性边界条件，波导两端区域设置完美匹配层模拟无限周期域，防止边界处产生反射声波，在压力声学模块下进行计算。图中Pi表示入射声波，Pr表示反射波，Pi表示透射波，箭头表示声波的传播方向。超材料的厚度为d。

图6 仿真计算原理图

如图7(a)所示，一阶分形结构在其偶极共振频率745.9 Hz附近产生了负等效质量密度，负响应的频率范围为[760.2,1 173.9] Hz。如图7(b)所示，结构在单极共振频率987.9 Hz附近，产生了负等效体积模量，对应的频率范围为[564.7,1 013.7] Hz。

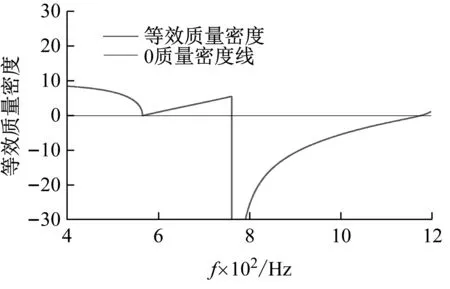
(a) 等效质量密度

如图8(a)所示，二阶分形结构在[404.2,423.4] Hz频率范围内有负等效质量密度，对应其偶极共振频率388.9 Hz。如图8(b)所示，在[210.1,574.8] Hz频率范围内有负等效体积模量，对应其单极共振频率328.4 Hz。

分形结构的单极共振频率附近产生负等效体积模量，偶极共振频率附近产生负等效质量密度。从一阶、二阶分形结构的等效声学参数可以看出，两者都存在负等效质量密度和负等效体积模量同时存在的频率范围，分别是[760.2,1 013.7]和[404.2,423.4] Hz，具有双负特性，相较于单负声学特性的结构，可以带来更多新颖的物理现象。计算出的负等效声学参数出现的频率范围，与带隙分布的频率范围相一致，验证了计算结果的准确性。

3.2 传递矩阵法

周期排列后的分形结构可以使声波发生全透射，还可以产生零相位差传输效应以及其它的新奇物理效应，可以用于新型声学功能器件的设计。其理论依据为，当超材料的动态质量密度ρe→0时，结构中等效声速ce→∞，这意味着背景声场中的声波经过超材料介质后，相位不会发生变化。由于多个分形单元之间存在共振耦合的作用，会影响其等效质量密度近零频率点的选取，因此，需要以周期排列的多个结构为研究对象进行计算。周期排列后的结构，不再满足于S参数法中的长波长尺寸条件，此时可采用一种评价均匀和各向同性材料的声学特性的方法：传递矩阵法，来分析周期性排列的分形结构的等效质量密度[23]。

(a) 等效质量密度

如图9(a)和10(a)所示，5×5排列的一阶分形结构在频率为786.3 Hz和977.7 Hz处质量密度接近于0。如图9(b)和10(b)所示，相应频率处存在声压透射峰值，透射系数接近于1，表明该频率下的声波经过分形结构时发生了全透射，没有能量的损耗，可以证明该频率点为质量密度近零频率点。

(a) 等效质量密度

计算多胞等效质量密度曲线，不仅可以找出其质量密度近零频率点，也可以用于验证带隙分布。如图10所示，在977.7 Hz之后的频率范围内，分形结构的动态等效质量密度逐渐降低成负值，并且在相应的透射系数图中可以看到，透射声压逐渐降低，这一频率范围与一阶分形结构的带隙区域[1 008.4,1 158.2]Hz是一致的。

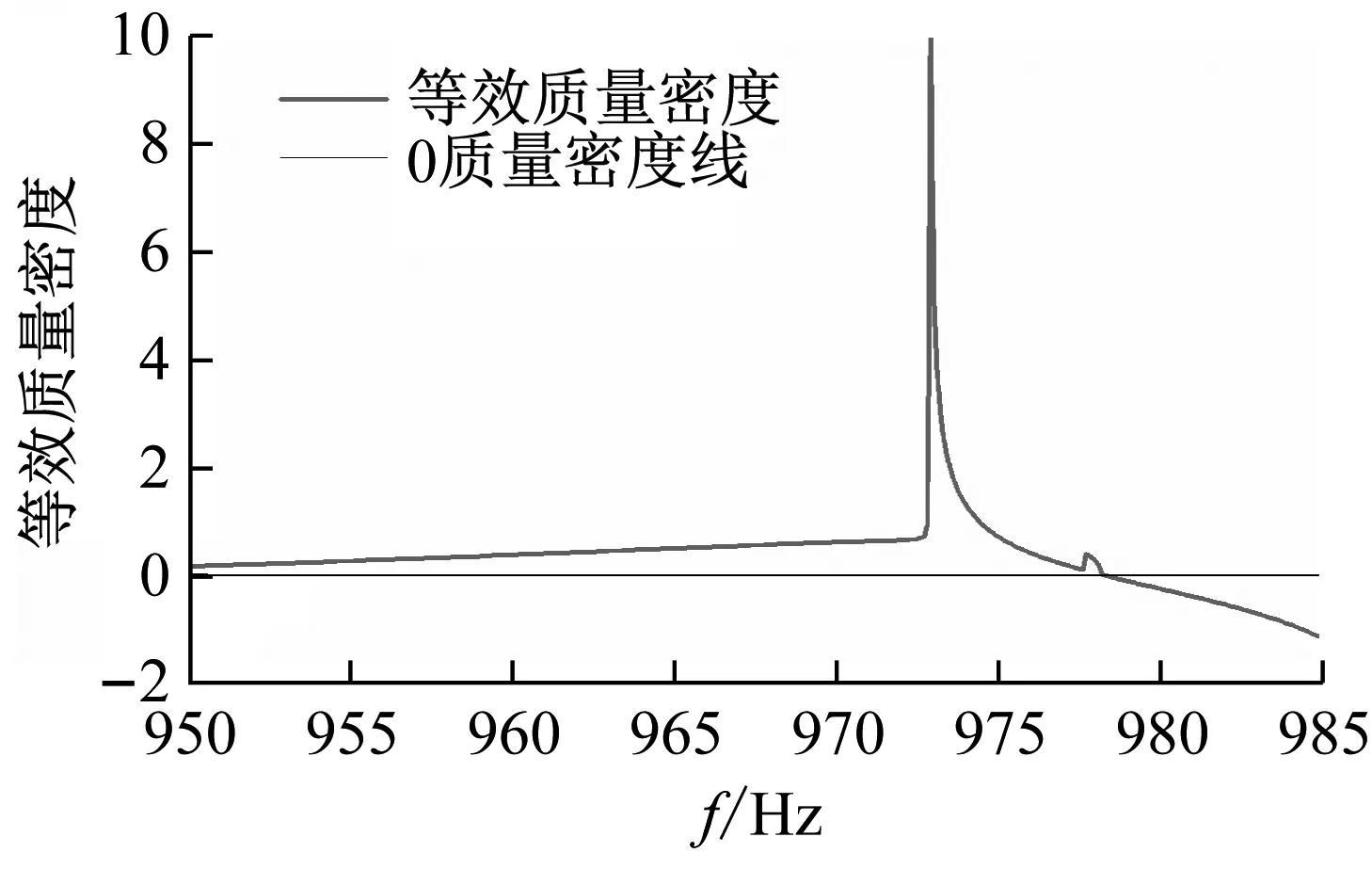
(a) 等效质量密度

如图11(a)和12(a)所示，5×5排列的二阶分形结构在频率为423.0 Hz、435.8 Hz和850.8 Hz、867.8 Hz处质量密度接近于0。图11(b)和12(b)表示的是，二阶结构在对应频率处存在声波透射系数峰值，透射系数接近于1。需要指出图12中，在845.0 Hz之前的频率范围内，二阶分形结构的等效质量密度为正值，但其声压透射系数接近于0，其原因在于二阶分形结构的动态等效体积模量为负值，也就是产生了单负声学响应，从而出现了禁声带隙，这一频率范围对应于上文中分析的二阶结构的禁声带隙[813.4,845.8] Hz。

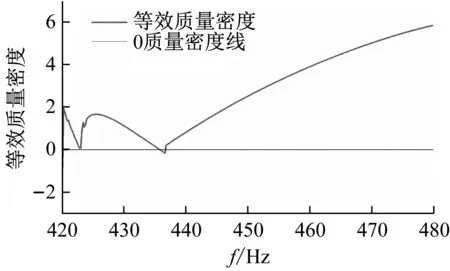
(a) 等效质量密度

(a) 等效质量密度

4 声波调控

通过以上分析可知，5×5排列的一阶、二阶分形结构，在特定频率点处动态等效质量密度接近于0。为了进一步说明周期排列的分形结构具有特殊的声学特性，可以在不同的单元数量和排列方式下进行声调控，在波导中对分形结构单元以不同位置分布(z型波导)、不同排列方式(5×7)的结构中放置障碍物，进行仿真分析。

4.1 近零密度传输

图13(a)和(b)分别表示频率为786.3 Hz和852.0 Hz的声波，经过一阶分形结构后波导中的声压分布。其中，图13(b)作为对照组来研究不为近零密度频率下的声波穿过分形结构后的声压分布。图14(a)和(b)表示波导中放置二阶分形结构，在频率分别为867.8 Hz和846.0 Hz处的声压分布。同样，图14(b)作为对比图来研究分形结构的声学特性。图13(c)和14(c)表示对应频率附近的声压透射系数。

(a) 786.3 Hz处的声压分布

在图13(a)和14(a)中，声波穿过周期排列的一阶、二阶分形结构后，幅值没有发生改变，近似以平面波的形式传播，波阵面中没有破坏点，很好的保持了平面波特征。而在图13(b)和14(b)中，不处于近零密度频率点的声波经过分形结构后，波形出现了扭曲，对比结果可以说明分形结构在近零密度频率点处可以很好的调控声波。在图13(c)和图14(c)中，结构在对应频率下的透射系数接近1，说明声波在传播过程中发生了全透射，没有能量的损耗，可以证明该频率点为近零密度频率点。需要指出的是，在图13(a)中，一阶分形结构填充的波导入射和出射两侧出现了零相位差效应，相位始终处于连续的状态，而在图14(a)中，二阶分形结构的两侧存在微小的相位改变。其原因在于，一阶分形结构的阻抗与空气阻抗不完全匹配，从而有反射波的存在，声波的叠加会产生相位的畸变[24]。

(a) 867.8 Hz处声压分布

4.2 波前整形

图15和16表示的是，在波导的入射端口与分形结构前表面之间，放置两个尺寸不一的圆形块来模拟不均匀散射声场，研究其对散射声场的整形作用。其中，图15(b)和图16(b)表示，在波导中不放置周期排列(5×5)的分形结构，近零密度频率下的声波的声场分布，可以看出，平面波受到圆形障碍物的干扰而变成杂乱无规律的散射声波，经过一段距离的传播后，在波导内仍然处于紊乱的状态。相对应的是，在图15(a)和16(a)中，散射声波通过分形结构后，波阵面重新变得规整，不再出现断裂、破坏的现象，并且近似于平面波，说明分形结构在质量密度近零频率处可以平整紊乱的声波，使其变得规整。

(a) 977.7 Hz处声压分布

(a) 850.8 Hz处声压分布

需要指出的是，在图15(c)中，近零密度频率点处的透射系数仅有0.65，同样在图16(c)中，最大透射系数也只有0.73。这是由于放置的两个圆形障碍物对声波起到了很大的反射作用，使得仅有部分声波传播至分形结构的表面，从而在计算出口端与入口段的声压之比时会出现透射系数不为1的情况。因为波前整形仿真与传递矩阵法找近零密度频率点时采用的排列方式(5×5)相同，调波频率点一致，故能证明该频率点为近零密度频率点。

4.3 声隐身

在周期排布的分形结构单元中间放置钢块，并将有限元分析模型的物理场条件设置为声固耦合，以考虑钢块振动对声场的影响作用。图17(b)和18(b)表示不同频率下的平面声波在有障碍物的波导中传播的声压分布图，这两个频率分别是一阶和二阶分形结构的近零密度频率。可以看出，声波经过钢块后，整体出现了散乱的状态，也没能还原成平面波。

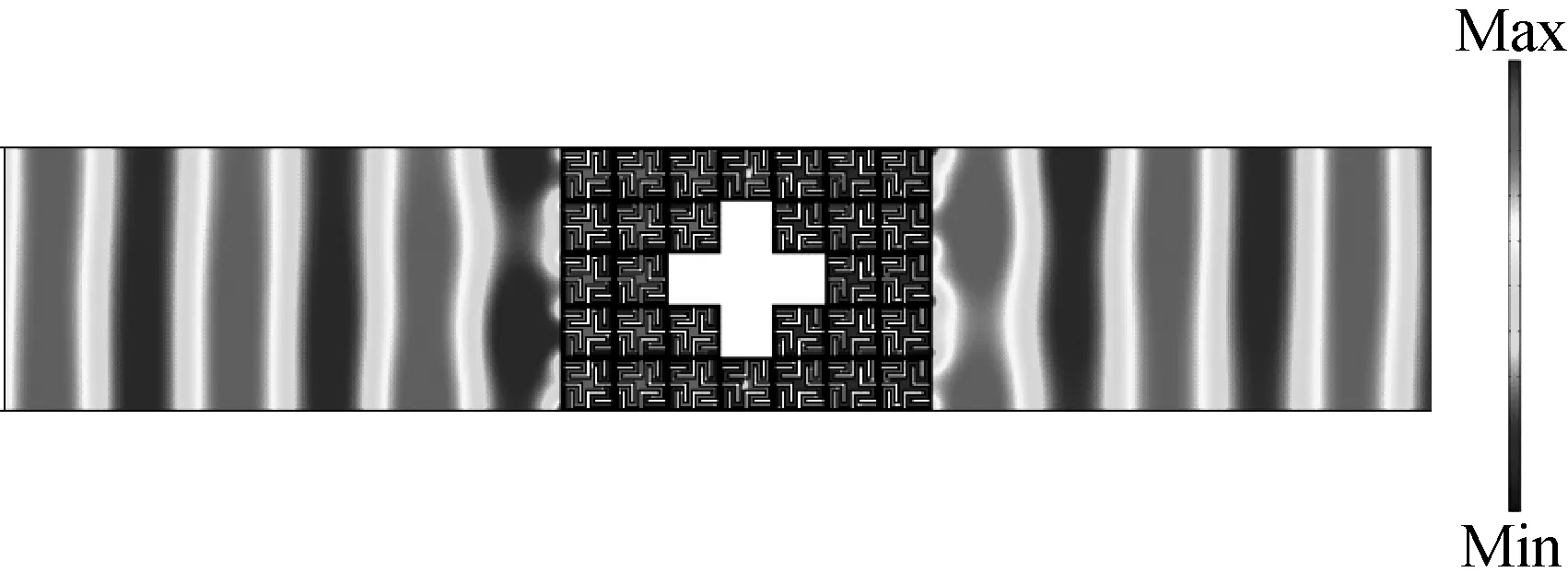
(a) 963.8 Hz处声压分布

从图17(a)和18(a)中可以发现，分形结构的内部存在声压分布，结构的两侧声波都为平面波，并且相位没有发生畸变，并且在图17(c)和18(c)中可以找到对应的近零密度频率处的透射系数接近于1，表明入射波经过分形结构及其内部包含的钢块后几乎发生了全透射，并且仍以平面波的形式继续传播，波阵面不存在明显的断裂和错位移动现象，整个系统变成了一个纯粹的自由空间。仿真结果有效地说明了分形结构可实现目标的声隐身，结构中的声场强度不为零，隐藏在其中的物体不能被探测到的同时能捕捉到外界的信号，允许物体与外界进行信息交流，解决了“盲”隐身的问题。

需要说明的是，如图17(a)所示，在频率为963.8 Hz的声压分布图中，分形结构前、后表面的声压分布与平面波传播特点有所区别，这是因为相对于图18(a)中852.2 Hz来说，频率增加以后波长减小，近场的不均匀性有所增加，声场存在一定的扰动。尽管如此，经过一定的传播距离后，声场又逐渐恢复了初始的波阵面性质，放置其中的物体得到了很好的隐藏，从这个角度来说，仍然很好地体现了声隐身的特点。

(a) 852.2 Hz处声压分布

4.4 声隧穿

为了说明分形结构不仅在定截面的平直波导中可以进行声调控，而且在突变截面、存在狭窄区域的曲折波导中，同样能起到调控作用，将两个波导错位排布，中间以z字形狭窄通道连接，在其中放置分形结构，分析声波通过狭窄通道的声隧穿效应。中间的狭窄区域可以视为一个声负载，不仅可以压缩声波而且会引起部分声波的反射。图19(b)和20(b)表示，在不放置分形结构的波导中，声波经过变截面的通道后被挤压和弯曲，进而变得散乱。而对比于图19(a)和20(a)，可以很明显的看出经过分形结构后的声波，其波阵面得到了很好的保持，进一步从透射系数图19(c)和20(c)中可以得到，该频率下的声波在传播过程中发生了全透射，能量近乎于零损耗，整个过程可以认为是一个解压还原的过程。证明了分形结构的声学特性完全不受通道的曲折度、截面的变化影响，可以应用于不同形状的通道。并且在这一部分中，选用的是二阶分形结构422.7 Hz的近零密度频率点来进行仿真计算，经过上述的比对分析，完全可以说明二阶分形结构独特的低频调波特性。总的来说，二阶分形结构的调波频段要低于一阶分形结构，因此可以通过增加分形结构的阶数，来实现对低频声波的调控。

(a) 982.0 Hz处声压分布

综上所述，(1) 在波前整形中，将一阶、二阶结构5×5排列，分形结构可以在质量密度近零频率点及其附近频率下规整声波；(2) 在变截面的波导如z型波导中排列分形结构，同样产生了近零密度传输现象，说明分形结构结构能够适应于不同的场景，有潜在的广泛应用前景；(3) 在5×7排列的分形结构中放置钢块，入射的声波经过整个系统后仍然保持着平面波的特征，说明分形结构能在低频下起到声隐身的作用，为声隐身提供了一个新的方法。(4) 进行声隧穿和声隐身仿真模拟时，选用了不同的分形结构单元数目，通过与5×5排列方式的比较，说明分形结构的声调控可以不受单元数量的限制；

(a) 422.7 Hz处声压分布

对比上文中一阶、二阶分形结构的透射系数曲线，可以看出二阶分形结构的声透射峰值多于一阶分形结构，表明随着分形阶数的增加，近零密度频率点数量增加，并且出现在更低频的范围内。

此外，在进行声波调控的过程中，以一阶分形结构为例，计算等效密度时选取的近零密度频率点为977.7 Hz，仿真中声隐身963.8 Hz，声隧穿982.0 Hz，质量密度近零频率点不一致。主要原因在于，不同数量、排列方式的多个单元之间存在共振耦合，造成了频率点不同程度的偏移[21]。

5 试验分析

如图21(a)所示，为了验证文中有限元分析方法的有效性，采用环氧树脂材料打印出一阶分形结构的三维模型，结构底部采用94 mm×99.8 mm×2 mm的基体板起固定支撑的作用。考虑到样品表面并非光滑界面，存在黏滞摩擦，因此仿真分析中选择了压力声学-热黏性声学模块下进行分析。图21(b)表示用于试验的阻抗管测试系统，其内部截面尺寸为100 mm×100 mm。

(a) 结构样品

图21(c)表示分形结构的试验测量与仿真计算的结果对比。可以看出，两条曲线总体趋势符合良好，说明了本文采用的有限元分析方法的有效性。但是，两条曲线存在幅值上的偏差和透射系数峰值频率的偏差，其中热黏性损耗只影响透射系数的幅值，并不会引起透射系数峰值频率的移动。仿真中三个峰值所在的频率分别是532 Hz、1 006 Hz和1 202 Hz，试验测试中则为540 Hz、1 050 Hz、1 262 Hz，对比三个峰值位置处的频率偏移大小，可以看出移动偏差最大位置在1 200 Hz附近，产生了60 Hz的偏移，但偏差只有5%。

通过多次的试验测量，峰值频率在低频范围内移动的原因可以归结于：① 模型底部的基体板的影响：基体板的存在阻碍了部分声波的传播。本文取基体板厚度初始值为2 mm，其作用为辅助构建分形声通道，而且由于打印模型时采用的材料为树脂材料，质量较轻，所以这一尺寸可以进行适度的调整，从而降低对实际测量的影响；② 3D打印过程的误差，即声通道的宽度存在一定量的偏差。

6 结 论

在[0,1 600] Hz频率范围内，一阶、二阶分形结构在各自的单极共振频率附近产生负体积密度，在偶极共振频率附近产生负体积模量，当结构的体积模量和质量密度中任意一个参数为负时，声波无法在其中传播，产生传播带隙。随着分形阶数的增加，分形结构产生的带隙数量增加，带隙面积从20.3%增加到21.6%，并逐渐向着更加低频的范围内移动，可以用于低频下的滤波。在质量密度接近于0的频率点处，周期排列的分形结构可以进行声波调控，如近零密度传输、波前整形、声隐身以及声隧穿，调控后声波以近似平面波的形式传播，且透射系数接近于1，声能量接近无损耗。