利用非对称阻尼切换控制车体升降的车高求解研究
蔡 琛, 姚嘉凌, 田松梅
(1.南京林业大学 汽车与交通工程学院,南京 210037;2.南京汽车集团 汽车工程研究院,南京 210028)
一般而言,悬架减振器的阻尼力并不对称相等,为有效减小冲击和振动,往往使悬架减振器伸张行程的阻尼大于压缩行程的阻尼,减振器阻尼呈现出非对称特性[1-2]。Warner[3]对具有压缩和伸张阻尼不对称特性的减振器进行试验时,首次发现簧载质量在路面激励下平衡位置下降。Rajalingham[4]在研究中也发现了这一现象,给出的解释是:悬架振动时,由于阻尼的不对称导致悬架弹簧的压缩量发生变化,从而引起簧载质量振动的平衡位置的下降。Balik[5]实验时发现,当伸张行程阻尼系数大于压缩行程阻尼系数时会引起车体下降,反之,伸张行程阻尼系数小于压缩行程阻尼系数时会引起车体上升。
非对称阻尼会使车体振动的平衡位置发生变化,受到这一现象的启发,本文创新性地提出了一种基于振动利用控制车体升降的思想方法。具体思路是根据车辆的行驶状态,通过控制半主动悬架阻尼可调减振器伸张和压缩行程的不对称阻尼来改变车体振动的平衡位置,该思想方法可应用于汽车高速转向、紧急避让等极端工况下的车高和姿态控制、主动防侧倾控制[6]等。例如,在高速转向时通过左右侧升降使车体向转弯方向倾斜的倾摆控制[7-9],可有效提高汽车操纵稳定性和迅速过弯能力,防止侧翻。
对于本文提出的通过控制半主动悬架阻尼可调减振器伸张和压缩行程的不对称阻尼来进行车高调节的系统来说,求解车体的升降高度,确定车体升降高度和不对称阻尼、车速、路面输入的对应关系是实施这种车体升降控制的前提,依据这种函数关系就可以在一定车速和路面工况下实时控制不对称阻尼以跟踪期望的升降高度。
分段线性系统传递率对于外界激励振幅具有独立性[10],也就是说在同一频率下输出响应和输入参数的均方根值比或峰值比是固定不变的。为探究车体升降高度和不对称阻尼、车速、路面输入的对应关系,从而求解车高,本文利用不对称阻尼悬架系统的这种传递率的独立性将其线性化,从而采用线性系统的求解方法求取路面激励下车体升降高度的响应。通过在不同路面激励、车速、阻尼不对称率工况下进行阻尼不对称分段线性系统的线性化,求解车体升降高度,通过函数拟合得到车体升降高度和不对称阻尼、车速、路面输入的对应关系。可以根据这种函数关系依据不同工况下车辆姿态的需求,调节不对称阻尼控制车体升降达到期望的车体高度。这种车体升降不仅是整车的同时升降,还包括左右两侧一升一降以控制车体的倾摆姿态,也可以是车体前后的一升一降以控制车体的俯仰姿态。最后通过仿真检验这种函数关系的准确性。
1 基于振动利用控制车体升降的基本思想和方法
为说明上述升降控制的思想方法,首先建立1/4车辆阻尼可调振动系统模型。根据牛顿第二定律,系统微分方程可表示为
(1)
式中:m2是簧载质量;m1是非簧载质量;k2是悬架刚度;k1是轮胎刚度;c2是悬架固有阻尼;z2是簧载质量位移;z1是非簧载质量位移;z0是路面输入;fd是可调阻尼力。
控制车体升降进行阻尼不对称切换控制的基本思想和方法是:
(1) 要控制车体下降,压缩行程采用小阻尼,伸张行程采用大阻尼,采用如下开关函数进行阻尼切换控制
(2)
式中:cm为大阻尼系数;c0为小阻尼系数。
(2) 要控制车体上升,压缩行程采用大阻尼,伸张行程采用小阻尼,采用如下开关函数进行阻尼切换控制
(3)
也可采用阻尼力切换控制的形式:
(1) 控制车体下降时采用
(4)
式中:fm为大阻尼力;f0为小阻尼力0。
(2) 控制车体上升时采用
(5)
为验证车体升降控制的有效性,进行仿真验证。设定B级路面下,车速20 m/s,仿真时间100 s,在50 s后,采用阻尼系数切换进行升降控制。其中仿真参数:m1=60 kg,m2=412 kg,k1=269 000 N·m-1,k2=26 000 N·m-1,c2=1 200 Ns/m。仿真结果如图1~图4所示。
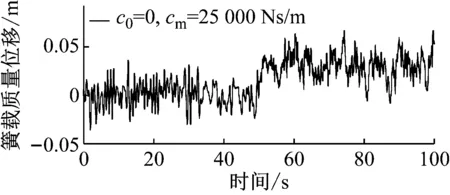
图1 车体上升控制(最大阻尼系数25 000 Ns/m)
图1~图2采用式(3)的控制策略进行车体上升控制。图1中c0=0,cm=25 000 Ns/m,车体平衡位置在50 s后迅速上升0.038 m;图2中c0=0,cm=50 000 Ns/m,车体平衡位置在50 s后迅速上升0.052 m。

图2 车体上升控制(最大阻尼系数50 000 Ns/m)
图3~图4采用式(2)的控制策略进行车体下降控制。图3中c0=0,cm=25 000 Ns/m,车体平衡位置在50 s后迅速下降0.038 m;图4中c0=0,cm=50 000 Ns/m,车体平衡位置在50 s后迅速下降0.052 m。
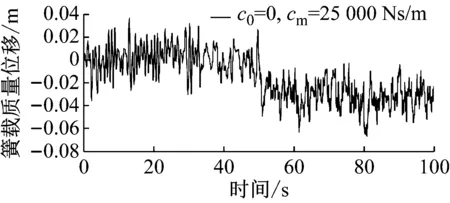
图3 车体下降控制(最大阻尼系数25 000 Ns/m)
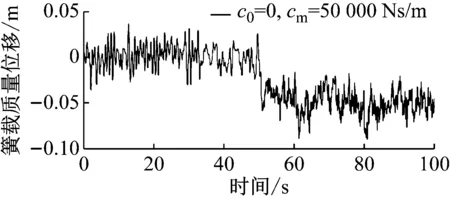
图4 车体下降控制(最大阻尼系数50 000 Ns/m)
从车体升降控制仿真结果可以看出,进行悬架不对称阻尼的调节可以有效升降车体的平衡位置,其最大阻尼力在4 000 N以内,属于普通可调阻尼减振器正常的阻尼力范围。对4个悬架可调减振器同时或分别进行升或降的控制,则可进行不同目的的车体姿态控制。
2 分段线性非线性系统线性化
为有效进行车体升降控制,需要研究车体升降高度与不对称阻尼、车速、路面输入等参数的变化规律,确定在一定工况下,车体升降高度与不对称阻尼的对应关系,从而控制阻尼升降车体到期望高度。由于分段线性系统是一种强非线性系统,不能通过线性系统的信号预测方法求解其车体振动的响应。但分段线性系统有一种非常有用的特性,即其传递率对于外界激励振幅具有独立性,不管激励振幅大小,它的传递率不变[11-12]。这种特性和线性系统的传递率特性是一样的,但这个传递率却不是实际的线性系统的传递率。因此,如果能将这种分段线性系统进行线性化,则车体升降高度就可以采用线性系统的求解方法进行求解。也就是在一定工况下,如果能求解出这种线性化后的传递率,则在已知路面输入的情况下通过传递率就可以知道要达到一定的车体升降高度需要的不对称阻尼力是多少。在此,首先将这种阻尼可调分段线性系统进行线性化。

(6)
式中:σz2(ωi)为悬架位移均方根值;σp(t)为正弦输入信号均方根值。图5为扫频获得的悬架位移传递率。

图5 传递率仿真
采用最小二乘法,用式(7)的函数对图5的传递率曲线进行拟合,结果如图6所示。
(7)

图6 悬架位移传递率拟合
拟合得到式(7)中的参数如表1所示。
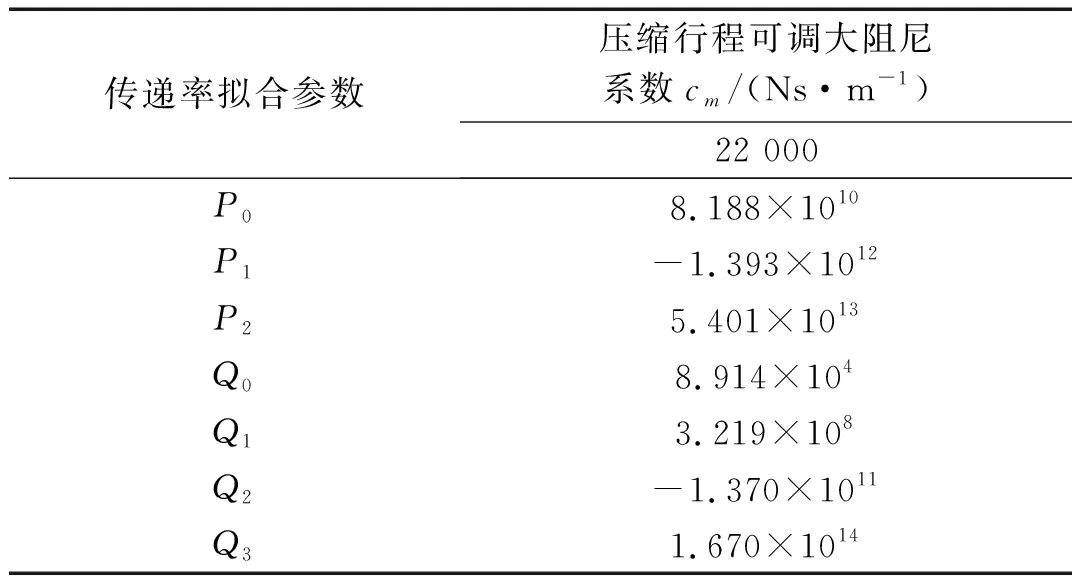
表1 传递率拟合参数
设计一个线性系统,使该线性系统的车体位移传递率与式(7)的分段线性系统车体位移传递率相等,此线性系统微分方程表达如下
(8)
频率响应函数表示为
(9)
取
Az2(ω)=|H(jω)|
(10)
可以得到ai,bi与拟合参数Pi,Qi之间的关系
(11)
根据由微分方程求状态空间表达式的方法,假设以p(t)作为输入,u1(t)=z2(t)-C0p(t)作为第一分量及输出,进一步将微分方程(8)写成一阶线性微分系统
(12)
式中,u1(t)=y(t),p(t)=x(t)。将式(12)代入式(8),使得输入信号的各阶导数项系数为0,可以得到Ci与ai,bi的关系
(13)
将式(12)写成状态空间方程为
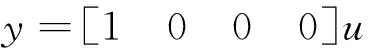
(14)
其中:
(15)
其特征方程为
P(λ)=λ4+a1λ3+a2λ2+a3λ+a4
(16)
根据Hurwitz稳定性判据,此线性系统需要满足的稳定性条件为
a1>0,a2>0,a1a2-a3>0
(17)
通过上述方法,最终确定式(14)的线性系统具有与分段线性非线性悬架系统中簧载质量位移相同的传递率。在稳定性条件下求出系统参数,列举部分参数如表2所示。

表2 线性系统参数
3 车体升降高度求解
将分段线性非线性系统线性化后就可以采用线性系统理论进行相关分析和求解。由于求得了传递率,则簧载质量位移的功率谱密度可通过传递率和路面输入功率谱密度求出,如下式
(18)
其中路面输入的功率谱密度Gz0(ω)为
(19)
式中:v是车速(m/s);Gq(n0)是路面不平度系数(m3);n0是参考空间频率。
簧载质量位移的自相关函数Rx(τ)可以表示为

(20)
令时延τ=0,则
(21)
则簧载质量位移的均方值为
(22)
式中:ψz2为均方差;μz2为平均值。
因此,分段线性系统中悬架位移输出的均方根值可以近似表达为
(23)
式中,ωmin=2πfmin,ωmax=2πfmax是路面不平度引起的车辆振动的实际频率范围,其中fmin=0.3 Hz,fmax=30 Hz[12]。
采用第2章的方法分别求解不同不对称阻尼分段线性非线性悬架系统的线性化状态方程及其传递率。相似地,悬架系统固有阻尼c2取500 Ns/m,伸张行程可调阻尼系数取0,压缩行程可调阻尼系数间隔3 000 Ns/m取值,即可调阻尼系数取10 000,13 000,16 000,…,61 000 N,从而产生一系列不对称阻尼系数及对应的分段线性系统。在B级路面输入下分别求解车体的上升高度。其中n0=0.1 m-1,Gq(n0)=64×10-6m3。车速间隔10 km/h取值,即:v=40,50,…,110 km/h。通过公式(18)~(23)计算车体上升高度。部分数据如表3。

表3 B级路面下车体升降高度
B级路面车体上升高度与车速、压缩行程大阻尼系数的关系如图7所示。

图7 B级路面车体升降高度与压缩行程大阻尼系数、车速的关系
从图7可以看出:在同一车速下,随着压缩行程大阻尼系数不断增大,车体上升高度近似为线性增长;在同一压缩行程大阻尼系数下,随着车速不断增大,车体上升高度也近似为线性增长。
采用最小二乘法优化拟合,可以得到B级路面下的车体升降高度数学模型,如式(24)所示。
(24)
式中,
(25)
式中:H是车体升降高度(m);cm是压缩行程的可调大称阻尼系数(Ns/m);v是车速(m/s)。
拟合指标:SSE=0.000 7,R-square=0.978 7。其中SSE代表误差平方和,其越接近于0,曲线拟合效果越好。R-square为确定系数,通过数据的变化来表征拟合效果的好坏,确定系数的正常范围为0~1,其越接近于1,模型对数据拟合的越准确。
相似地,其他参数均不变,仅将路面等级设置为C级路面,可以得到C级路面车体上升高度与车速、压缩行程大阻尼系数的关系,如图8所示。

图8 C级路面车体升降高度与大阻尼系数、车速的关系
图8所显示的特征与上述相同,且对比B、C级路面的模型,可以发现当车速一定,压缩行程大阻尼系数一定时,C级路面的升降高度大于B级别路面。
采用最小二乘法优化拟合,可以得到C级路面下的车体升降高度数学模型,如(26)所示。
(26)
式中,
(27)
拟合指标:SSE=0.003 0,R-square=0.978 7,表明拟合结果精确度高。
式(24)、(26)为伸张行程的可调阻尼系数取0,压缩行程的间隔取可调大阻尼系数得到的B级路面、C级路面车体升降函数。如果反过来,压缩行程可调阻尼系数取0,伸张行程间隔取可调大阻尼系数,则可以得到一样的函数,只不过车体升降高度变成负号,限于篇幅,在此略去求解过程。
4 车体升降高度求解模型的准确度校验
为验证车体升降高度数学模型的准确性,进行仿真验证。分别采用B级路面、C级路面作为输入,采用式(3)的控制策略进行车体上升控制,将仿真结果与模型式(24)、(26)的计算结果对比,部分数据如表4~5、表6、表7所示。
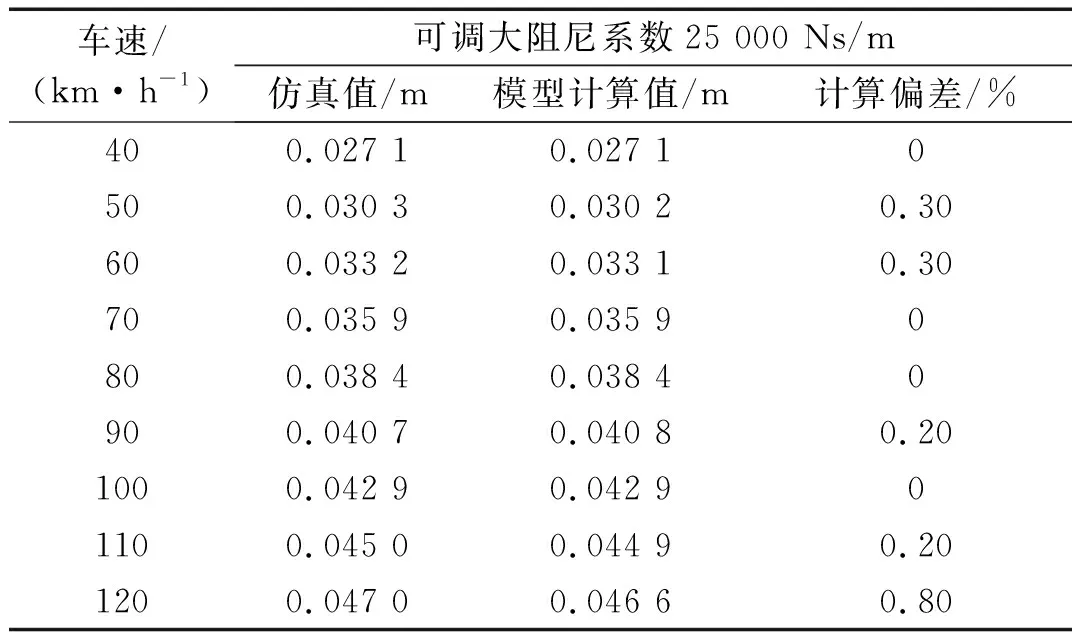
表4 B级路面车体升降高度仿真与模型计算比1
表4表示B级路面下,采用压缩行程可调阻尼系数25 000 Ns/m,伸张行程可调阻尼系数为0的控制策略,在不同车速下的仿真高度以及采用式(24)的模型进行计算的升降高度。当路面输入一定、大阻尼系数一定时,车速越高车体升降越大。
表5表示B级路面下,恒定车速为72 km/h,采用压缩行程可调阻尼系数为25 000~56 000 Ns/m,伸张行程阻尼系数为0的控制策略下的仿真高度以及采用式(24)的模型进行计算的升降高度。当路面输入一定、车速一定时,可调阻尼系数越大,车体上升越大,同时表5的误差结果表明式(24)的模型具有较高的精度。

表5 B级路面车体升降高度仿真与模型计算对比2
表6表示C级路面下,采用压缩行程可调阻尼系数为25 000 Ns/m,伸张行程阻尼系数为0的控制策略,在不同车速下的仿真高度以及采用式(26)的模型进行计算的升降高度。当路面输入一定、可调阻尼系数一定时,车速越高车体升降越大;同时与表5的结果对比表明,在相同的可调阻尼系数及车速下,C级路面下的车体升降高度明显高于B级路面。

表6 C级路面车体升降高度仿真与模型计算对比1
表7表示C级路面下,恒定车速为72 km/h,采用压缩行程可调阻尼系数25 000~56 000 Ns/m,伸张行程可调阻尼系数为0的控制策略下的仿真高度以及采用式(26)的模型进行计算的升降高度。当路面输入一定、车速一定时,可调阻尼系数越大,车体升降越大,同时误差结果表明式(26)的模型具有较高的精度。

表7 C级路面车体升降高度仿真与模型计算对比2
因此,所求解的车体升降高度函数能够较为准确地描述阻尼可调减振器悬架系统在B级、C级路面输入下,车体升降高度与不对称阻尼系数、车速之间的关系,为阻尼可调减振器的车高控制提供了依据。
5 结 论
(1) 悬架的非对称阻尼会使车体振动的平衡位置发生变化,受到这一现象的启发提出基于振动利用控制车体升降并给出了阻尼控制的切换函数,仿真证明了该思想方法能有效实施车体的升降控制。
(2) 汽车4个阻尼可调悬架的单独升降控制既可进行整车的同时升降,也可进行车体姿态的控制。
(3) 利用分段线性系统传递率对于外界激励振幅具有独立性的特性,通过扫频激励得到此系统的传递率,通过对这个传递率曲线进行拟合求得该传递率的函数表达,同时设计一种与此分段线性系统具有相同传递率的线性系统,进而可以通过线性系统的求解方法求取车体升降高度的均方根值。
(4) 通过在不同路面激励、车速、阻尼不对称率工况下进行阻尼不对称分段线性系统的线性化,求解车体升降高度,通过函数拟合得到车体升降高度和不对称阻尼、车速、路面输入的对应关系,并对函数预测车体升降高度的准确性进行了验证。利用这种函数关系就可以在不同行驶工况下,通过调节不对称阻尼控制车体升降高度达到期望值。

